黑龙江省哈尔滨市南岗区虹桥中学2023-2024学年九年级(上)开学数学试卷(五四学制)(含解析)
文档属性
| 名称 | 黑龙江省哈尔滨市南岗区虹桥中学2023-2024学年九年级(上)开学数学试卷(五四学制)(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 632.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 00:00:00 | ||
图片预览


文档简介
2023-2024学年黑龙江省哈尔滨市南岗区虹桥中学九年级(上)开学数学试卷(五四学制)
一、选择题(每小题3分,共计30分)
1.(3分)(﹣3)2的计算结果是( )
A.﹣9 B.﹣6 C.9 D.6
2.(3分)下列运算正确的是( )
A.a10÷a2=a5 B.a2 a3=a6
C.(a+b)2=a2+b2 D.(a+b)(a﹣b)=a2﹣b2
3.(3分)观察下列银行标志,从图案看不是轴对称图形的是( )
A. B. C. D.
4.(3分)下列函数:①y=2x ②y=③y=2x+1 ④y=2x2+1,其中一次函数的个数是( )
A.4 B.3 C.2 D.1
5.(3分)已知一次函数y=kx+b的图象过二、三、四象限,则下列结论正确的是( )
A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<0
6.(3分)如图,一次函数y=mx+n与正比例函数y=mnx(m、n是常数,且mm≠0)的图象的是( )
A.①和③ B.②和③ C.①和④ D.②和④
7.(3分)某型号的手机连续两次降价,每个售价由原来的1185元降到了580元,设平均每次降价的百分率为x,列出方程正确的是( )
A.580(1+x)2=1185 B.1185(1+x)2=580
C.580(1﹣x)2=1185 D.1185(1﹣x)2=580
8.(3分)分式方程的解为( )
A.x=﹣1 B.x=1 C.x=2 D.x=3
9.(3分)一元二次方程x2﹣6x﹣5=0配方可变形为( )
A.(x﹣3)2=14 B.(x﹣3)2=4 C.(x+3)2=14 D.(x+3)2=4
10.(3分)如图,E是平行四边形ABCD的边BA延长线上的一点,CE交AD于点F,下列各式中错误的是( )
A. B. C. D.
二、填空题(每小题3分,共计30分)
11.(3分)将数0.312用科学记数法表示为 .
12.(3分)在函数中,自变量x的取值范围是 .
13.(3分)把多项式2mx2﹣2m分解因式的结果是 .
14.(3分)不等式组的整数解为 .
15.(3分)已知y=(m﹣1)x|m|+m+2,y是x的一次函数,则m= .
16.(3分)已知直线y=﹣2x+1向下平移m(m>0)个单位后经过点(1,﹣3),则m的值为 .
17.(3分)已知等腰三角形的底角是30°,腰长为2,则它的周长是 .
18.(3分)若x2﹣4x+m2是完全平方式,则m= .
19.(3分)已知△ABC中,AB=AC,且有一个内角等于30°,点B关于直线AC的对称点为E,连接BE和CE,则∠BEC= .
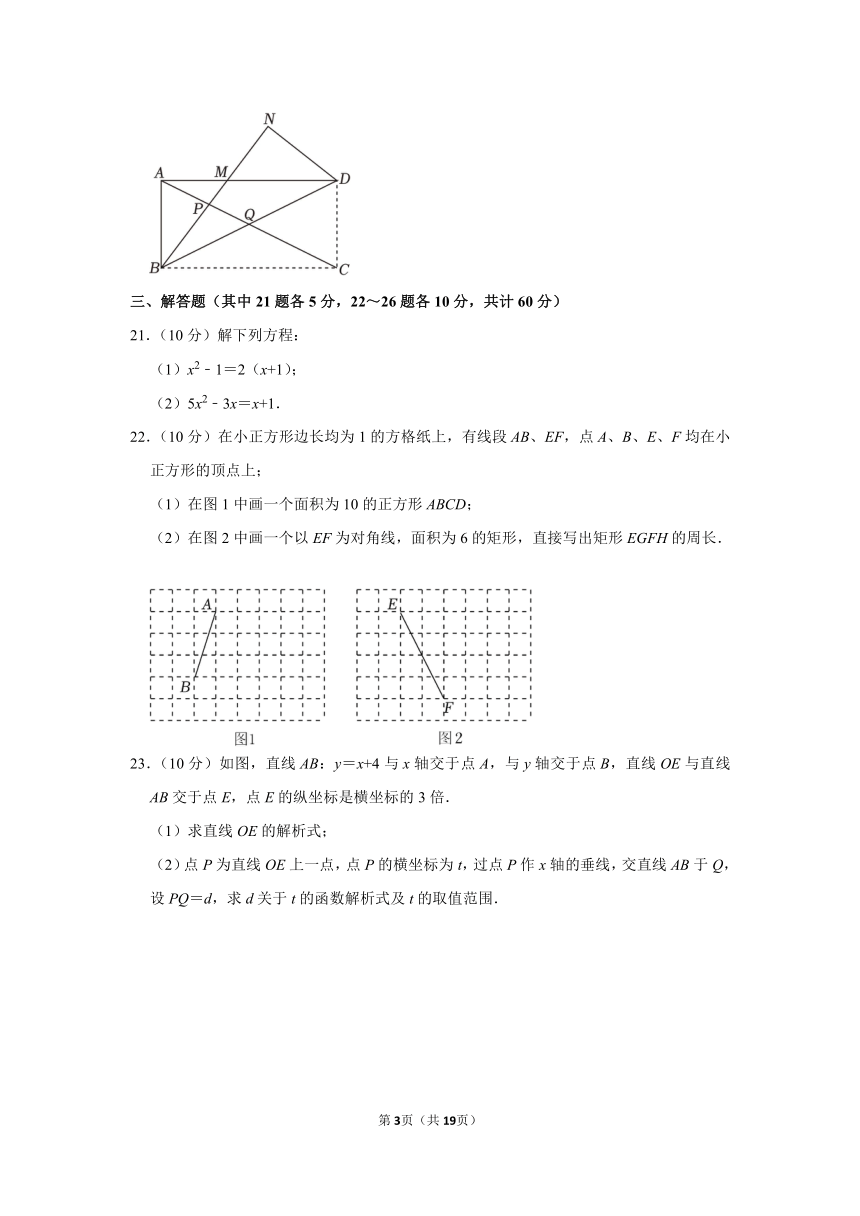
20.(3分)如图,将矩形ABCD沿对角线BD翻折,点C的对应点是点N,BN与AC交于点P,与AD交于点M,若PQ:QC=5:11,AB=4,则PQ= .
三、解答题(其中21题各5分,22~26题各10分,共计60分)
21.(10分)解下列方程:
(1)x2﹣1=2(x+1);
(2)5x2﹣3x=x+1.
22.(10分)在小正方形边长均为1的方格纸上,有线段AB、EF,点A、B、E、F均在小正方形的顶点上;
(1)在图1中画一个面积为10的正方形ABCD;
(2)在图2中画一个以EF为对角线,面积为6的矩形,直接写出矩形EGFH的周长.
23.(10分)如图,直线AB:y=x+4与x轴交于点A,与y轴交于点B,直线OE与直线AB交于点E,点E的纵坐标是横坐标的3倍.
(1)求直线OE的解析式;
(2)点P为直线OE上一点,点P的横坐标为t,过点P作x轴的垂线,交直线AB于Q,设PQ=d,求d关于t的函数解析式及t的取值范围.
24.(10分)已知在平行四边形ABCD中,E是边DA的延长线上一点,且AE=AD,连结EC,分别交AB、BD于点F、G.
(1)如图1,求证:AF=BF;
(2)如图2,当∠ADC=90°时,在不添加辅助线、不添加字母的情况下,请找出图中等于△EAF面积的2倍所有直角三角形.
25.(10分)某商店以每件16元的价格购进一批商品,物价局限定每件商品的利润不得超过30%.
(1)根据物价局规定,此商品每件售价最高可定为多少?
(2)若每件商品售价定为x元,则每天可卖出(170﹣5x)件,商店预期每天要盈利280元,那么每件商品的售价应定为多少元?
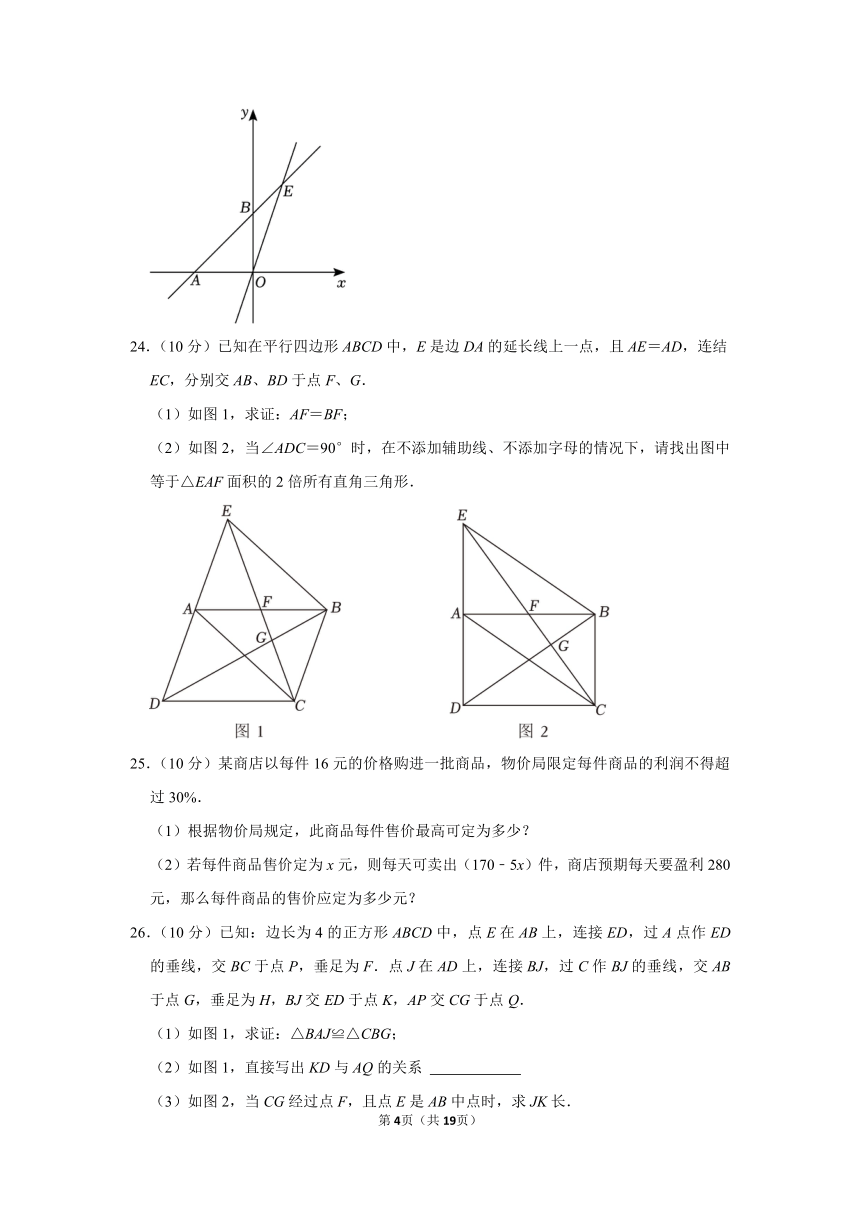
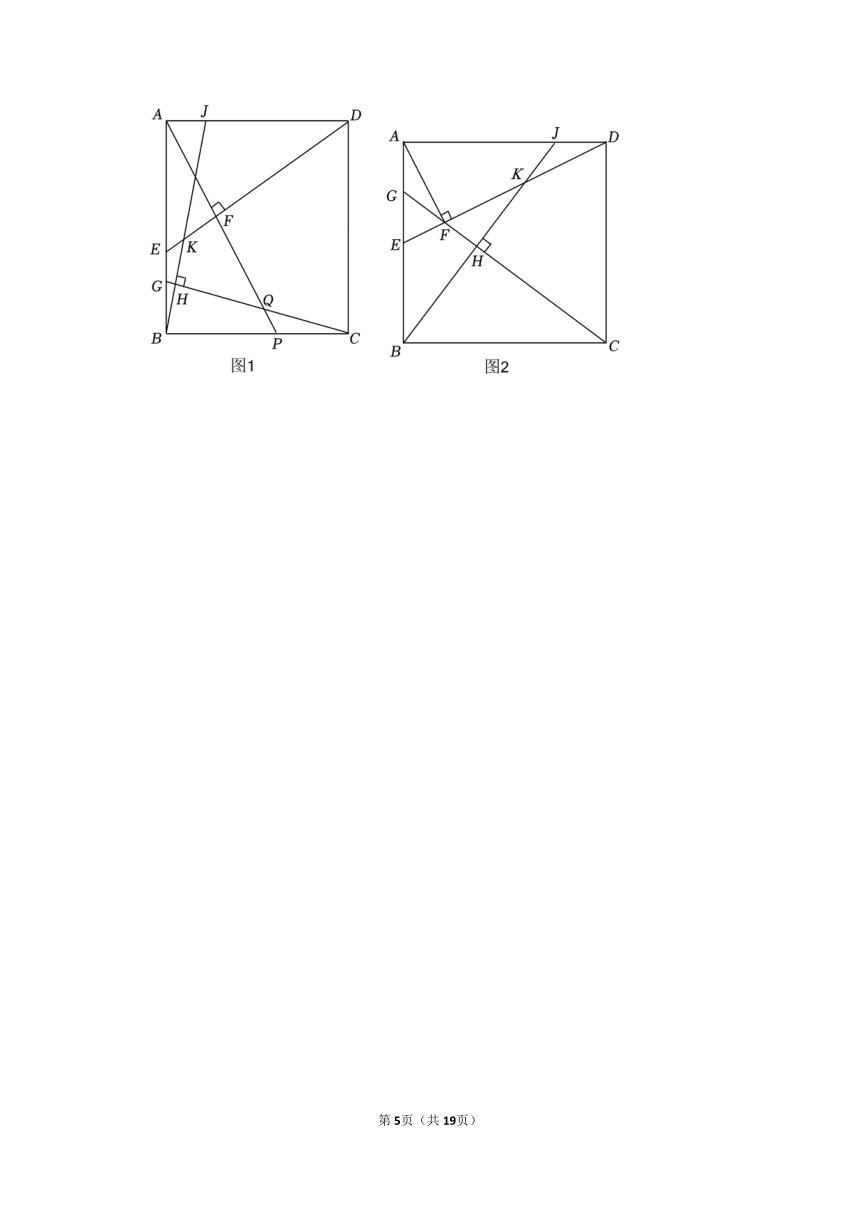
26.(10分)已知:边长为4的正方形ABCD中,点E在AB上,连接ED,过A点作ED的垂线,交BC于点P,垂足为F.点J在AD上,连接BJ,过C作BJ的垂线,交AB于点G,垂足为H,BJ交ED于点K,AP交CG于点Q.
(1)如图1,求证:△BAJ≌△CBG;
(2)如图1,直接写出KD与AQ的关系
(3)如图2,当CG经过点F,且点E是AB中点时,求JK长.
2023-2024学年黑龙江省哈尔滨市南岗区虹桥中学九年级(上)开学数学试卷(五四学制)
参考答案与试题解析
一、选择题(每小题3分,共计30分)
1.(3分)(﹣3)2的计算结果是( )
A.﹣9 B.﹣6 C.9 D.6
【解答】解:根据有理数的乘方,(﹣3)2=9.
故选:C.
2.(3分)下列运算正确的是( )
A.a10÷a2=a5 B.a2 a3=a6
C.(a+b)2=a2+b2 D.(a+b)(a﹣b)=a2﹣b2
【解答】解:A、a10÷a2=a8,故此选项错误;
B、a2 a3=a5,故此选项错误;
C、(a+b)2=a2+2ab+b2,故此选项错误;
D、(a+b)(a﹣b)=a2﹣b2,正确.
故选:D.
3.(3分)观察下列银行标志,从图案看不是轴对称图形的是( )
A. B. C. D.
【解答】解:A、不是轴对称图形,故本选项正确;
B、是轴对称图形,故本选项错误;
C、是轴对称图形,故本选项错误;
D、是轴对称图形,故本选项错误.
故选:A.
4.(3分)下列函数:①y=2x ②y=③y=2x+1 ④y=2x2+1,其中一次函数的个数是( )
A.4 B.3 C.2 D.1
【解答】解:①y=2x是一次函数;
②y=是一次函数;
③y=2x+1是一次函数;
④y=2x2+1,自变量次数不是1,故不是一次函数.
综上,是一次函数的有①②③,共3个.
故选:B.
5.(3分)已知一次函数y=kx+b的图象过二、三、四象限,则下列结论正确的是( )
A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<0
【解答】解:∵一次函数y=kx+b的图象经过第二,三,四象限,
∴k<0,b<0,
故选:D.
6.(3分)如图,一次函数y=mx+n与正比例函数y=mnx(m、n是常数,且mm≠0)的图象的是( )
A.①和③ B.②和③ C.①和④ D.②和④
【解答】解:①当mn>0,m,n同号,y=mnx的图象经过一、三象限,
同正时y=mx+n的图象经过一、二、三象限,同负时过二、三、四象限,只有④符合题意;
②当mn<0时,m,n异号,y=mnx的图象经过二,四象限,
则y=mx+n过一、三、四象限或一,二、四象限,只有②符合题意;
故选:D.
7.(3分)某型号的手机连续两次降价,每个售价由原来的1185元降到了580元,设平均每次降价的百分率为x,列出方程正确的是( )
A.580(1+x)2=1185 B.1185(1+x)2=580
C.580(1﹣x)2=1185 D.1185(1﹣x)2=580
【解答】解:设平均每次降价的百分率为x,
由题意得出方程为:1185(1﹣x)2=580.
故选:D.
8.(3分)分式方程的解为( )
A.x=﹣1 B.x=1 C.x=2 D.x=3
【解答】解:方程的两边同乘2x(x+3),得
x+3=4x,
解得x=1.
检验:把x=1代入2x(x+3)=8≠0.
∴原方程的解为:x=1.
故选:B.
9.(3分)一元二次方程x2﹣6x﹣5=0配方可变形为( )
A.(x﹣3)2=14 B.(x﹣3)2=4 C.(x+3)2=14 D.(x+3)2=4
【解答】解:x2﹣6x﹣5=0,
x2﹣6x=5,
x2﹣6x+9=14,
所以(x﹣3)2=14.
故选:A.
10.(3分)如图,E是平行四边形ABCD的边BA延长线上的一点,CE交AD于点F,下列各式中错误的是( )
A. B. C. D.
【解答】解:∵AD∥BC
∴
∵CD∥BE
∴△CDF∽△EBC
∴,
∴
∵AD∥BC
∴△AEF∽△EBC
∴
∴D错误.
故选:D.
二、填空题(每小题3分,共计30分)
11.(3分)将数0.312用科学记数法表示为 3.12×10﹣1 .
【解答】解:将数0.312用科学记数法表示为3.12×10﹣1.
故答案为:3.12×10﹣1.
12.(3分)在函数中,自变量x的取值范围是 x≠6 .
【解答】解:由题意,得
x﹣6≠0,
解得x≠6,
故答案为:x≠6.
13.(3分)把多项式2mx2﹣2m分解因式的结果是 2m(x+1)(x﹣1) .
【解答】解:2mx2﹣2m=2m(x2﹣1)
=2m(x+1)(x﹣1).
故答案为:2m(x+1)(x﹣1).
14.(3分)不等式组的整数解为 x=2 .
【解答】解:
解不等式①得:x<3,
解不等式②得:x>1,
∴不等式组的解集为1<x<3,
∴整数解为:x=2.
故答案为:x=2.
15.(3分)已知y=(m﹣1)x|m|+m+2,y是x的一次函数,则m= ﹣1 .
【解答】解:由题意得:|m|=1,且m﹣1≠0,
解得:m=﹣1,
故答案为:﹣1.
16.(3分)已知直线y=﹣2x+1向下平移m(m>0)个单位后经过点(1,﹣3),则m的值为 2 .
【解答】解:将直线y=﹣2x+1向下平移m(m>0)个单位后所得直线为:y=﹣2x+1﹣m.
将点(1,﹣3)代入,得﹣2+1﹣m=﹣3.
解得m=2.
故答案为:2.
17.(3分)已知等腰三角形的底角是30°,腰长为2,则它的周长是 6 .
【解答】解:作AD⊥BC于D,
∵AB=AC,
∴BD=DC,
在Rt△ABD中,∠B=30°,
∴AD=AB=,
由勾股定理得,BD==3,
∴BC=2BD=6,
∴△ABC的周长为:6+2+2=6+4,
故答案为:6+4.
18.(3分)若x2﹣4x+m2是完全平方式,则m= ±2 .
【解答】解:∵x2﹣4x+m2=x2﹣2x 2+m2,
∴m2=22=4,
∴m=±2.
故答案为:±2.
19.(3分)已知△ABC中,AB=AC,且有一个内角等于30°,点B关于直线AC的对称点为E,连接BE和CE,则∠BEC= 15°或60° .
【解答】解:当底角是30°时,
∵∠ACB=30°,B与E关于AC对称,
∴∠CBO=∠BEC,∠EOC=∠BOC=90°,
∴∠BEC=∠EBC=60°
当顶角是30°时,
∵∠A=30°,B与E关于AC对称,AB=AC,
∴∠ACB=,
∴∠CBO=∠BEC,∠EOC=∠BOC=90°,
∴∠BEC=∠EBC=90°﹣75°=15°,
故答案为:15°或60°.
20.(3分)如图,将矩形ABCD沿对角线BD翻折,点C的对应点是点N,BN与AC交于点P,与AD交于点M,若PQ:QC=5:11,AB=4,则PQ= .
【解答】解:∵PQ:QC=5:11,矩形ABCD中AQ=QC,
∴PQ:AC=5:22,
∴AP:PQ:QC=6:5:11,
∵AM∥BC,
∴AM:BC=AP:PC=6:16=3:8,
∴AM:MD=3:5,
∵AB=ND,∠BAM=∠DNM,∠AMB=∠NMD,
∴△BAM≌△DNM(AAS),
∴NM=AM,MD=NB,
∴AM:MB=3:5,
设AM=3x,MB=5x,
∵AB=4,
∴(3x)2+42=(5x)2,
∴x=1,AM=3,MD=MB=5,
∴AD=8,AC=BD==4,
∴PQ=AC=.
三、解答题(其中21题各5分,22~26题各10分,共计60分)
21.(10分)解下列方程:
(1)x2﹣1=2(x+1);
(2)5x2﹣3x=x+1.
【解答】解:(1)x2﹣1=2(x+1),
(x+1)(x﹣1)﹣2(x+1)=0,
(x+1)(x﹣1﹣2)=0,
(x+1)(x﹣3)=0,
x+1=0或x﹣3=0,
x1=﹣1,x2=3;
(2)5x2﹣3x=x+1,
整理得:5x2﹣4x﹣1=0,
(x﹣1)(5x+1)=0,
x﹣1=0或5x+1=0,
x1=1,x2=﹣.
22.(10分)在小正方形边长均为1的方格纸上,有线段AB、EF,点A、B、E、F均在小正方形的顶点上;
(1)在图1中画一个面积为10的正方形ABCD;
(2)在图2中画一个以EF为对角线,面积为6的矩形,直接写出矩形EGFH的周长.
【解答】解:(1)如图1中,正方形ABCD即为所求;
(2)如图2中,矩形EGFH即为所求.
∵EG=,GF=3,
∴矩形EGFH的周长=2(+3)=.
23.(10分)如图,直线AB:y=x+4与x轴交于点A,与y轴交于点B,直线OE与直线AB交于点E,点E的纵坐标是横坐标的3倍.
(1)求直线OE的解析式;
(2)点P为直线OE上一点,点P的横坐标为t,过点P作x轴的垂线,交直线AB于Q,设PQ=d,求d关于t的函数解析式及t的取值范围.
【解答】解:(1)∵点E的纵坐标是横坐标的3倍,
∴设点E的坐标为(m,3m),
又∵点E在直线y=x+4上,
∴3m=m+4,
解得:m=2,
∴点E的坐标为(2,6),
设直线OE的解析式为y=kx(k≠0),
将点E(2,6)代入y=kx,得:6=2k,解得:k=3,
∴直线OE的解析式为y=3x,
(2)∵PQ⊥x轴,
∴点P与点Q的横坐标相同,均为t,
∵点P在直线OE上,点Q在直线AB上,
∴点P的坐标为(t,3t),点Q的坐标为(t,t+4),①当点P在点E的下方时,即:t<2,如图:
此时,PQ=d=t+4﹣3t=﹣2t+4,
②当点P与点Q重合时,即:t=2,
此时,PQ=d=0,
③当点P在点E的上方时,即:t>2,如图:
PQ=d=3t﹣(t+4)=2t﹣4,
综上所述:d关于t的函数解析式为:.
24.(10分)已知在平行四边形ABCD中,E是边DA的延长线上一点,且AE=AD,连结EC,分别交AB、BD于点F、G.
(1)如图1,求证:AF=BF;
(2)如图2,当∠ADC=90°时,在不添加辅助线、不添加字母的情况下,请找出图中等于△EAF面积的2倍所有直角三角形.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠AEF=∠BCF,
∵AE=AD,
∴AE=BC,
∵∠AFE=∠BFC,
∴△AEF≌△BCF(AAS),
∴AF=BF;
(2)当∠ADC=90°时,四边形ABCD是矩形,
和(1)同理可得△AEF≌△BCF,
∴AF=BF,
∴2S△EAF=S△ABE,
∵图中与△ABE面积相等的直角三角形有:△ADC,△ABC,△ADB,△BCD,
故图中等于△EAF面积的2倍的直角三角形有:△ADC,△ABC,△ADB,△BCD,△ABE.
25.(10分)某商店以每件16元的价格购进一批商品,物价局限定每件商品的利润不得超过30%.
(1)根据物价局规定,此商品每件售价最高可定为多少?
(2)若每件商品售价定为x元,则每天可卖出(170﹣5x)件,商店预期每天要盈利280元,那么每件商品的售价应定为多少元?
【解答】解:(1)16(1+30%)=20.8,
答:此商品每件售价最高可定为20.8元.
(2)(x﹣16)(170﹣5x)=280,
整理,得:x2﹣50x+600=0,
解得:x1=20,x2=30,
因为售价最高不得高于20.8元,所以x2=30不合题意应舍去.
答:每件商品的售价应定为20元.
26.(10分)已知:边长为4的正方形ABCD中,点E在AB上,连接ED,过A点作ED的垂线,交BC于点P,垂足为F.点J在AD上,连接BJ,过C作BJ的垂线,交AB于点G,垂足为H,BJ交ED于点K,AP交CG于点Q.
(1)如图1,求证:△BAJ≌△CBG;
(2)如图1,直接写出KD与AQ的关系 KD=AQ
(3)如图2,当CG经过点F,且点E是AB中点时,求JK长.
【解答】(1)证明:∵四边形ABCD是正方形,
∴∠BAD=∠ABC=90°,AB=BC=CD=AD=4,
∵BJ⊥CG,
∴∠BHG=90°,
∴∠ABJ+∠AJB=90°,∠ABJ+∠BGH=90°,
∴∠AJB=∠BGC,
在Rt△BAJ和Rt△CBG中,
,
∴Rt△BAJ≌Rt△CBG(AAS),
即△BAJ≌△CBG;
(2)解:由(1)可知,△BAJ≌△CBG,
∴AJ=BG,∠AJB=∠BGC,
∵AB=AD,∠AJB+∠BJD=180°,∠BGC+∠AGC=180°,
∴AD﹣AJ=AB﹣BG,即JD=GA,∠DJK=∠AGQ,
∵∠BAD=90°,AF⊥DE,
∴∠GAQ+∠QAD=90°,∠QAD+∠ADK=90°,
∴∠GAQ=∠JDK,
在△DJK和△AGQ中,
,
∴△DJK≌△AGQ(ASA),
∴KD=QA,
故答案为:KD=AQ;
(3)解:∵点E是AB 的中点,
∴AE=BE=B=x4=2.
在Rt△ADE中,AD=AB=4,
∴DE===2,
∵AF⊥DE,S△ADE==,
∴=,
在Rt△AEF中,EF===,
∴=,
∵四边形ABCD是正方形,
∴AB∥CD,
∴∠GEF=∠CDF,∠EGF=∠DCF,
∴△EFG∽△DFC,
∴,且CD=AB=4,
∴GE===1,且AE=2,
∴点G是AE的中点,
在Rt△AEF中,GF===1,
∴BG=BE+EG=2+1=3.
在Rt△BCG中,CG===5,
∵BH⊥CG,S△BCG=BG BC=CG GH,
∴BH=,
在Rt△BCH 中,CH===,
∴FH=CG﹣CH﹣FG=5﹣1﹣=,
∵点G是AE的中点,
则AG=GF=GE,
∴∠GFE=∠GEF=∠KFH,
在Rt△AEF和Rt△FHK中,∠GEF+∠EAF=90°,∠KFH+∠FKH=90°,
∠EAF=∠FKH,且∠AFE=∠KHF=90°,
∴Rt△AEF∽Rt△KFH,
∴,EF=,AF=,FH=,
∴KH==,
在Rt△ABJ和Rt△BHG中,∠ABJ+∠AJB=90°,∠ABJ+∠BGH=90°,
∴∠BGH=∠AJB,
在△ABJ和△CBG中,
,
∴△ABJ≌△CBG中(AAS),
∴BJ=CG=5,且BH=,HK=,
∴JK=BJ﹣BH﹣HK=5﹣=1,
∴JK长为1.
第1页(共1页)
一、选择题(每小题3分,共计30分)
1.(3分)(﹣3)2的计算结果是( )
A.﹣9 B.﹣6 C.9 D.6
2.(3分)下列运算正确的是( )
A.a10÷a2=a5 B.a2 a3=a6
C.(a+b)2=a2+b2 D.(a+b)(a﹣b)=a2﹣b2
3.(3分)观察下列银行标志,从图案看不是轴对称图形的是( )
A. B. C. D.
4.(3分)下列函数:①y=2x ②y=③y=2x+1 ④y=2x2+1,其中一次函数的个数是( )
A.4 B.3 C.2 D.1
5.(3分)已知一次函数y=kx+b的图象过二、三、四象限,则下列结论正确的是( )
A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<0
6.(3分)如图,一次函数y=mx+n与正比例函数y=mnx(m、n是常数,且mm≠0)的图象的是( )
A.①和③ B.②和③ C.①和④ D.②和④
7.(3分)某型号的手机连续两次降价,每个售价由原来的1185元降到了580元,设平均每次降价的百分率为x,列出方程正确的是( )
A.580(1+x)2=1185 B.1185(1+x)2=580
C.580(1﹣x)2=1185 D.1185(1﹣x)2=580
8.(3分)分式方程的解为( )
A.x=﹣1 B.x=1 C.x=2 D.x=3
9.(3分)一元二次方程x2﹣6x﹣5=0配方可变形为( )
A.(x﹣3)2=14 B.(x﹣3)2=4 C.(x+3)2=14 D.(x+3)2=4
10.(3分)如图,E是平行四边形ABCD的边BA延长线上的一点,CE交AD于点F,下列各式中错误的是( )
A. B. C. D.
二、填空题(每小题3分,共计30分)
11.(3分)将数0.312用科学记数法表示为 .
12.(3分)在函数中,自变量x的取值范围是 .
13.(3分)把多项式2mx2﹣2m分解因式的结果是 .
14.(3分)不等式组的整数解为 .
15.(3分)已知y=(m﹣1)x|m|+m+2,y是x的一次函数,则m= .
16.(3分)已知直线y=﹣2x+1向下平移m(m>0)个单位后经过点(1,﹣3),则m的值为 .
17.(3分)已知等腰三角形的底角是30°,腰长为2,则它的周长是 .
18.(3分)若x2﹣4x+m2是完全平方式,则m= .
19.(3分)已知△ABC中,AB=AC,且有一个内角等于30°,点B关于直线AC的对称点为E,连接BE和CE,则∠BEC= .
20.(3分)如图,将矩形ABCD沿对角线BD翻折,点C的对应点是点N,BN与AC交于点P,与AD交于点M,若PQ:QC=5:11,AB=4,则PQ= .
三、解答题(其中21题各5分,22~26题各10分,共计60分)
21.(10分)解下列方程:
(1)x2﹣1=2(x+1);
(2)5x2﹣3x=x+1.
22.(10分)在小正方形边长均为1的方格纸上,有线段AB、EF,点A、B、E、F均在小正方形的顶点上;
(1)在图1中画一个面积为10的正方形ABCD;
(2)在图2中画一个以EF为对角线,面积为6的矩形,直接写出矩形EGFH的周长.
23.(10分)如图,直线AB:y=x+4与x轴交于点A,与y轴交于点B,直线OE与直线AB交于点E,点E的纵坐标是横坐标的3倍.
(1)求直线OE的解析式;
(2)点P为直线OE上一点,点P的横坐标为t,过点P作x轴的垂线,交直线AB于Q,设PQ=d,求d关于t的函数解析式及t的取值范围.
24.(10分)已知在平行四边形ABCD中,E是边DA的延长线上一点,且AE=AD,连结EC,分别交AB、BD于点F、G.
(1)如图1,求证:AF=BF;
(2)如图2,当∠ADC=90°时,在不添加辅助线、不添加字母的情况下,请找出图中等于△EAF面积的2倍所有直角三角形.
25.(10分)某商店以每件16元的价格购进一批商品,物价局限定每件商品的利润不得超过30%.
(1)根据物价局规定,此商品每件售价最高可定为多少?
(2)若每件商品售价定为x元,则每天可卖出(170﹣5x)件,商店预期每天要盈利280元,那么每件商品的售价应定为多少元?
26.(10分)已知:边长为4的正方形ABCD中,点E在AB上,连接ED,过A点作ED的垂线,交BC于点P,垂足为F.点J在AD上,连接BJ,过C作BJ的垂线,交AB于点G,垂足为H,BJ交ED于点K,AP交CG于点Q.
(1)如图1,求证:△BAJ≌△CBG;
(2)如图1,直接写出KD与AQ的关系
(3)如图2,当CG经过点F,且点E是AB中点时,求JK长.
2023-2024学年黑龙江省哈尔滨市南岗区虹桥中学九年级(上)开学数学试卷(五四学制)
参考答案与试题解析
一、选择题(每小题3分,共计30分)
1.(3分)(﹣3)2的计算结果是( )
A.﹣9 B.﹣6 C.9 D.6
【解答】解:根据有理数的乘方,(﹣3)2=9.
故选:C.
2.(3分)下列运算正确的是( )
A.a10÷a2=a5 B.a2 a3=a6
C.(a+b)2=a2+b2 D.(a+b)(a﹣b)=a2﹣b2
【解答】解:A、a10÷a2=a8,故此选项错误;
B、a2 a3=a5,故此选项错误;
C、(a+b)2=a2+2ab+b2,故此选项错误;
D、(a+b)(a﹣b)=a2﹣b2,正确.
故选:D.
3.(3分)观察下列银行标志,从图案看不是轴对称图形的是( )
A. B. C. D.
【解答】解:A、不是轴对称图形,故本选项正确;
B、是轴对称图形,故本选项错误;
C、是轴对称图形,故本选项错误;
D、是轴对称图形,故本选项错误.
故选:A.
4.(3分)下列函数:①y=2x ②y=③y=2x+1 ④y=2x2+1,其中一次函数的个数是( )
A.4 B.3 C.2 D.1
【解答】解:①y=2x是一次函数;
②y=是一次函数;
③y=2x+1是一次函数;
④y=2x2+1,自变量次数不是1,故不是一次函数.
综上,是一次函数的有①②③,共3个.
故选:B.
5.(3分)已知一次函数y=kx+b的图象过二、三、四象限,则下列结论正确的是( )
A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<0
【解答】解:∵一次函数y=kx+b的图象经过第二,三,四象限,
∴k<0,b<0,
故选:D.
6.(3分)如图,一次函数y=mx+n与正比例函数y=mnx(m、n是常数,且mm≠0)的图象的是( )
A.①和③ B.②和③ C.①和④ D.②和④
【解答】解:①当mn>0,m,n同号,y=mnx的图象经过一、三象限,
同正时y=mx+n的图象经过一、二、三象限,同负时过二、三、四象限,只有④符合题意;
②当mn<0时,m,n异号,y=mnx的图象经过二,四象限,
则y=mx+n过一、三、四象限或一,二、四象限,只有②符合题意;
故选:D.
7.(3分)某型号的手机连续两次降价,每个售价由原来的1185元降到了580元,设平均每次降价的百分率为x,列出方程正确的是( )
A.580(1+x)2=1185 B.1185(1+x)2=580
C.580(1﹣x)2=1185 D.1185(1﹣x)2=580
【解答】解:设平均每次降价的百分率为x,
由题意得出方程为:1185(1﹣x)2=580.
故选:D.
8.(3分)分式方程的解为( )
A.x=﹣1 B.x=1 C.x=2 D.x=3
【解答】解:方程的两边同乘2x(x+3),得
x+3=4x,
解得x=1.
检验:把x=1代入2x(x+3)=8≠0.
∴原方程的解为:x=1.
故选:B.
9.(3分)一元二次方程x2﹣6x﹣5=0配方可变形为( )
A.(x﹣3)2=14 B.(x﹣3)2=4 C.(x+3)2=14 D.(x+3)2=4
【解答】解:x2﹣6x﹣5=0,
x2﹣6x=5,
x2﹣6x+9=14,
所以(x﹣3)2=14.
故选:A.
10.(3分)如图,E是平行四边形ABCD的边BA延长线上的一点,CE交AD于点F,下列各式中错误的是( )
A. B. C. D.
【解答】解:∵AD∥BC
∴
∵CD∥BE
∴△CDF∽△EBC
∴,
∴
∵AD∥BC
∴△AEF∽△EBC
∴
∴D错误.
故选:D.
二、填空题(每小题3分,共计30分)
11.(3分)将数0.312用科学记数法表示为 3.12×10﹣1 .
【解答】解:将数0.312用科学记数法表示为3.12×10﹣1.
故答案为:3.12×10﹣1.
12.(3分)在函数中,自变量x的取值范围是 x≠6 .
【解答】解:由题意,得
x﹣6≠0,
解得x≠6,
故答案为:x≠6.
13.(3分)把多项式2mx2﹣2m分解因式的结果是 2m(x+1)(x﹣1) .
【解答】解:2mx2﹣2m=2m(x2﹣1)
=2m(x+1)(x﹣1).
故答案为:2m(x+1)(x﹣1).
14.(3分)不等式组的整数解为 x=2 .
【解答】解:
解不等式①得:x<3,
解不等式②得:x>1,
∴不等式组的解集为1<x<3,
∴整数解为:x=2.
故答案为:x=2.
15.(3分)已知y=(m﹣1)x|m|+m+2,y是x的一次函数,则m= ﹣1 .
【解答】解:由题意得:|m|=1,且m﹣1≠0,
解得:m=﹣1,
故答案为:﹣1.
16.(3分)已知直线y=﹣2x+1向下平移m(m>0)个单位后经过点(1,﹣3),则m的值为 2 .
【解答】解:将直线y=﹣2x+1向下平移m(m>0)个单位后所得直线为:y=﹣2x+1﹣m.
将点(1,﹣3)代入,得﹣2+1﹣m=﹣3.
解得m=2.
故答案为:2.
17.(3分)已知等腰三角形的底角是30°,腰长为2,则它的周长是 6 .
【解答】解:作AD⊥BC于D,
∵AB=AC,
∴BD=DC,
在Rt△ABD中,∠B=30°,
∴AD=AB=,
由勾股定理得,BD==3,
∴BC=2BD=6,
∴△ABC的周长为:6+2+2=6+4,
故答案为:6+4.
18.(3分)若x2﹣4x+m2是完全平方式,则m= ±2 .
【解答】解:∵x2﹣4x+m2=x2﹣2x 2+m2,
∴m2=22=4,
∴m=±2.
故答案为:±2.
19.(3分)已知△ABC中,AB=AC,且有一个内角等于30°,点B关于直线AC的对称点为E,连接BE和CE,则∠BEC= 15°或60° .
【解答】解:当底角是30°时,
∵∠ACB=30°,B与E关于AC对称,
∴∠CBO=∠BEC,∠EOC=∠BOC=90°,
∴∠BEC=∠EBC=60°
当顶角是30°时,
∵∠A=30°,B与E关于AC对称,AB=AC,
∴∠ACB=,
∴∠CBO=∠BEC,∠EOC=∠BOC=90°,
∴∠BEC=∠EBC=90°﹣75°=15°,
故答案为:15°或60°.
20.(3分)如图,将矩形ABCD沿对角线BD翻折,点C的对应点是点N,BN与AC交于点P,与AD交于点M,若PQ:QC=5:11,AB=4,则PQ= .
【解答】解:∵PQ:QC=5:11,矩形ABCD中AQ=QC,
∴PQ:AC=5:22,
∴AP:PQ:QC=6:5:11,
∵AM∥BC,
∴AM:BC=AP:PC=6:16=3:8,
∴AM:MD=3:5,
∵AB=ND,∠BAM=∠DNM,∠AMB=∠NMD,
∴△BAM≌△DNM(AAS),
∴NM=AM,MD=NB,
∴AM:MB=3:5,
设AM=3x,MB=5x,
∵AB=4,
∴(3x)2+42=(5x)2,
∴x=1,AM=3,MD=MB=5,
∴AD=8,AC=BD==4,
∴PQ=AC=.
三、解答题(其中21题各5分,22~26题各10分,共计60分)
21.(10分)解下列方程:
(1)x2﹣1=2(x+1);
(2)5x2﹣3x=x+1.
【解答】解:(1)x2﹣1=2(x+1),
(x+1)(x﹣1)﹣2(x+1)=0,
(x+1)(x﹣1﹣2)=0,
(x+1)(x﹣3)=0,
x+1=0或x﹣3=0,
x1=﹣1,x2=3;
(2)5x2﹣3x=x+1,
整理得:5x2﹣4x﹣1=0,
(x﹣1)(5x+1)=0,
x﹣1=0或5x+1=0,
x1=1,x2=﹣.
22.(10分)在小正方形边长均为1的方格纸上,有线段AB、EF,点A、B、E、F均在小正方形的顶点上;
(1)在图1中画一个面积为10的正方形ABCD;
(2)在图2中画一个以EF为对角线,面积为6的矩形,直接写出矩形EGFH的周长.
【解答】解:(1)如图1中,正方形ABCD即为所求;
(2)如图2中,矩形EGFH即为所求.
∵EG=,GF=3,
∴矩形EGFH的周长=2(+3)=.
23.(10分)如图,直线AB:y=x+4与x轴交于点A,与y轴交于点B,直线OE与直线AB交于点E,点E的纵坐标是横坐标的3倍.
(1)求直线OE的解析式;
(2)点P为直线OE上一点,点P的横坐标为t,过点P作x轴的垂线,交直线AB于Q,设PQ=d,求d关于t的函数解析式及t的取值范围.
【解答】解:(1)∵点E的纵坐标是横坐标的3倍,
∴设点E的坐标为(m,3m),
又∵点E在直线y=x+4上,
∴3m=m+4,
解得:m=2,
∴点E的坐标为(2,6),
设直线OE的解析式为y=kx(k≠0),
将点E(2,6)代入y=kx,得:6=2k,解得:k=3,
∴直线OE的解析式为y=3x,
(2)∵PQ⊥x轴,
∴点P与点Q的横坐标相同,均为t,
∵点P在直线OE上,点Q在直线AB上,
∴点P的坐标为(t,3t),点Q的坐标为(t,t+4),①当点P在点E的下方时,即:t<2,如图:
此时,PQ=d=t+4﹣3t=﹣2t+4,
②当点P与点Q重合时,即:t=2,
此时,PQ=d=0,
③当点P在点E的上方时,即:t>2,如图:
PQ=d=3t﹣(t+4)=2t﹣4,
综上所述:d关于t的函数解析式为:.
24.(10分)已知在平行四边形ABCD中,E是边DA的延长线上一点,且AE=AD,连结EC,分别交AB、BD于点F、G.
(1)如图1,求证:AF=BF;
(2)如图2,当∠ADC=90°时,在不添加辅助线、不添加字母的情况下,请找出图中等于△EAF面积的2倍所有直角三角形.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠AEF=∠BCF,
∵AE=AD,
∴AE=BC,
∵∠AFE=∠BFC,
∴△AEF≌△BCF(AAS),
∴AF=BF;
(2)当∠ADC=90°时,四边形ABCD是矩形,
和(1)同理可得△AEF≌△BCF,
∴AF=BF,
∴2S△EAF=S△ABE,
∵图中与△ABE面积相等的直角三角形有:△ADC,△ABC,△ADB,△BCD,
故图中等于△EAF面积的2倍的直角三角形有:△ADC,△ABC,△ADB,△BCD,△ABE.
25.(10分)某商店以每件16元的价格购进一批商品,物价局限定每件商品的利润不得超过30%.
(1)根据物价局规定,此商品每件售价最高可定为多少?
(2)若每件商品售价定为x元,则每天可卖出(170﹣5x)件,商店预期每天要盈利280元,那么每件商品的售价应定为多少元?
【解答】解:(1)16(1+30%)=20.8,
答:此商品每件售价最高可定为20.8元.
(2)(x﹣16)(170﹣5x)=280,
整理,得:x2﹣50x+600=0,
解得:x1=20,x2=30,
因为售价最高不得高于20.8元,所以x2=30不合题意应舍去.
答:每件商品的售价应定为20元.
26.(10分)已知:边长为4的正方形ABCD中,点E在AB上,连接ED,过A点作ED的垂线,交BC于点P,垂足为F.点J在AD上,连接BJ,过C作BJ的垂线,交AB于点G,垂足为H,BJ交ED于点K,AP交CG于点Q.
(1)如图1,求证:△BAJ≌△CBG;
(2)如图1,直接写出KD与AQ的关系 KD=AQ
(3)如图2,当CG经过点F,且点E是AB中点时,求JK长.
【解答】(1)证明:∵四边形ABCD是正方形,
∴∠BAD=∠ABC=90°,AB=BC=CD=AD=4,
∵BJ⊥CG,
∴∠BHG=90°,
∴∠ABJ+∠AJB=90°,∠ABJ+∠BGH=90°,
∴∠AJB=∠BGC,
在Rt△BAJ和Rt△CBG中,
,
∴Rt△BAJ≌Rt△CBG(AAS),
即△BAJ≌△CBG;
(2)解:由(1)可知,△BAJ≌△CBG,
∴AJ=BG,∠AJB=∠BGC,
∵AB=AD,∠AJB+∠BJD=180°,∠BGC+∠AGC=180°,
∴AD﹣AJ=AB﹣BG,即JD=GA,∠DJK=∠AGQ,
∵∠BAD=90°,AF⊥DE,
∴∠GAQ+∠QAD=90°,∠QAD+∠ADK=90°,
∴∠GAQ=∠JDK,
在△DJK和△AGQ中,
,
∴△DJK≌△AGQ(ASA),
∴KD=QA,
故答案为:KD=AQ;
(3)解:∵点E是AB 的中点,
∴AE=BE=B=x4=2.
在Rt△ADE中,AD=AB=4,
∴DE===2,
∵AF⊥DE,S△ADE==,
∴=,
在Rt△AEF中,EF===,
∴=,
∵四边形ABCD是正方形,
∴AB∥CD,
∴∠GEF=∠CDF,∠EGF=∠DCF,
∴△EFG∽△DFC,
∴,且CD=AB=4,
∴GE===1,且AE=2,
∴点G是AE的中点,
在Rt△AEF中,GF===1,
∴BG=BE+EG=2+1=3.
在Rt△BCG中,CG===5,
∵BH⊥CG,S△BCG=BG BC=CG GH,
∴BH=,
在Rt△BCH 中,CH===,
∴FH=CG﹣CH﹣FG=5﹣1﹣=,
∵点G是AE的中点,
则AG=GF=GE,
∴∠GFE=∠GEF=∠KFH,
在Rt△AEF和Rt△FHK中,∠GEF+∠EAF=90°,∠KFH+∠FKH=90°,
∠EAF=∠FKH,且∠AFE=∠KHF=90°,
∴Rt△AEF∽Rt△KFH,
∴,EF=,AF=,FH=,
∴KH==,
在Rt△ABJ和Rt△BHG中,∠ABJ+∠AJB=90°,∠ABJ+∠BGH=90°,
∴∠BGH=∠AJB,
在△ABJ和△CBG中,
,
∴△ABJ≌△CBG中(AAS),
∴BJ=CG=5,且BH=,HK=,
∴JK=BJ﹣BH﹣HK=5﹣=1,
∴JK长为1.
第1页(共1页)
同课章节目录
