4.2.1等差数列的概念(第一课时) 课件(共22张PPT)
文档属性
| 名称 | 4.2.1等差数列的概念(第一课时) 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 405.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 11:46:00 | ||
图片预览








文档简介
(共22张PPT)
4.2.1 等差数列的概念
(第一课时)
教学目标:目录
1
2
理解等差数列、等差中项的概念
掌握求等差数列的通项公式
教学重点、难点:目录
运用等差数列通项公式解决相关问题
目录
CONTENTS
一、情景引入
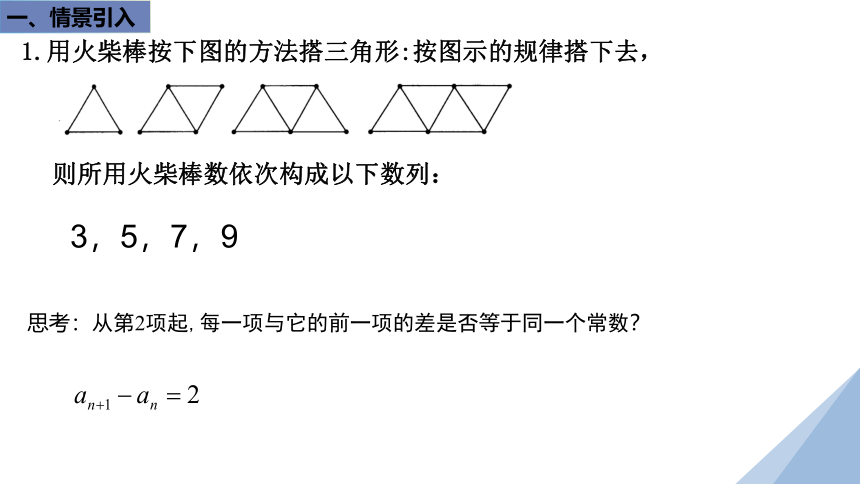
1.用火柴棒按下图的方法搭三角形:按图示的规律搭下去,
思考:从第2项起,每一项与它的前一项的差是否等于同一个常数?
则所用火柴棒数依次构成以下数列:
3,5,7,9
目录
CONTENTS
一、情景引入
2.北京天坛圜丘坛的地面是由石板铺成,最中间是圆形的天心石,围绕天心石的是9圈扇环形的石板,从内到外的石板数依次为:
9,18,27,36,45,54,63,72,81.
思考:从第2项起,每一项与它的前一项的差是否等于同一个常数?
目录
CONTENTS
一、情景引入
3.某人向银行贷款a万元,贷款时间为n年。如果个人贷款利率为r,那么按照等额本金方式还款,他从某月开始,每月应还本金b(=)万元,每月支付给银行的利息(单位:万元)依次为:
(注:每月归还本金=贷款总额
利息部分=(贷款总额-已归还本金累计额)
思考:从第2项起,每一项与它的前一项的差是否等于同一个常数?
目录
二、合作探究(一)
等差数列定义:
一般地,如果一个数列从第2项起,每一项与前一项的差都等于同一个常数,就称这个数列为等差数列,这个常数就称为等差数列的公差,用d来表示。
目录
三、例题讲解
例题1:判断下列数列是否为等差数列,若是,求出首项和公差.
(1) 100,90,80,70,60,50 ;
(2) 9,9.9,9.99,9.999,9.9999;
(3) 1,-1,1,-1,1,-1;
(4) 1, , 0, -,
是
不是
不是
是
目录
三、例题讲解
例题2:观察如下几组数,在两数中插入什么数后,三个数就会成为一个等差数列?
①-1, ,9;②6, ,6;③0, ,4
如果在a与b中间插入一个数A,使a, A, b成等差数列,
那么A叫做a与b的等差中项。
思考:如果在a与b中间插入一个数A,使a, A, b成等差数列, A=?
4
6
2
四、课堂练习
1.数列{an}中,an=an+1-1,a1=2,则a5=
四、课堂练习
2.数列{an}中,2an+1=an+2+an,已知相邻三项分别为3,b,7,则b=
二、合作探究(二)
思考:如果已知一个等差数列的首项是 a1 ,公差是 d ,那么如何求出这个数列的通项an ?
二、合作探究(二)
思考:如果已知一个等差数列的首项是 a1 ,公差是 d ,那么如何求出这个数列的通项an ?
三、例题讲解
例1 (1) 已知等差数列{an}的通项公式为an=5-2n,求{an}公差和首项;
(2) 求等差数列 8,5,2,···的第20项.
三、例题讲解
例1 (1) 已知等差数列{an}的通项公式为an=5-2n,求{an}公差和首项;
(2) 求等差数列 8,5,2,···的第20项.
三、例题讲解
例2 -401是不是等差数列 -5,-9,-13,…的项?如果是,是第几项?
四、课堂练习
四、课堂练习
四、课堂练习
五、课堂小结
等差数列定义:
一般地,如果一个数列从第2项起,每一项与前一项的差都等于同一个常数,就称这个数列为等差数列,这个常数就称为等差数列的公差,用d来表示。
如果在a与b中间插入一个数A,使a, A, b成等差数列,
那么A叫做a与b的。
等差中项:
等差数通项公式:
六、作业
THANKS
4.2.1 等差数列的概念
(第一课时)
教学目标:目录
1
2
理解等差数列、等差中项的概念
掌握求等差数列的通项公式
教学重点、难点:目录
运用等差数列通项公式解决相关问题
目录
CONTENTS
一、情景引入
1.用火柴棒按下图的方法搭三角形:按图示的规律搭下去,
思考:从第2项起,每一项与它的前一项的差是否等于同一个常数?
则所用火柴棒数依次构成以下数列:
3,5,7,9
目录
CONTENTS
一、情景引入
2.北京天坛圜丘坛的地面是由石板铺成,最中间是圆形的天心石,围绕天心石的是9圈扇环形的石板,从内到外的石板数依次为:
9,18,27,36,45,54,63,72,81.
思考:从第2项起,每一项与它的前一项的差是否等于同一个常数?
目录
CONTENTS
一、情景引入
3.某人向银行贷款a万元,贷款时间为n年。如果个人贷款利率为r,那么按照等额本金方式还款,他从某月开始,每月应还本金b(=)万元,每月支付给银行的利息(单位:万元)依次为:
(注:每月归还本金=贷款总额
利息部分=(贷款总额-已归还本金累计额)
思考:从第2项起,每一项与它的前一项的差是否等于同一个常数?
目录
二、合作探究(一)
等差数列定义:
一般地,如果一个数列从第2项起,每一项与前一项的差都等于同一个常数,就称这个数列为等差数列,这个常数就称为等差数列的公差,用d来表示。
目录
三、例题讲解
例题1:判断下列数列是否为等差数列,若是,求出首项和公差.
(1) 100,90,80,70,60,50 ;
(2) 9,9.9,9.99,9.999,9.9999;
(3) 1,-1,1,-1,1,-1;
(4) 1, , 0, -,
是
不是
不是
是
目录
三、例题讲解
例题2:观察如下几组数,在两数中插入什么数后,三个数就会成为一个等差数列?
①-1, ,9;②6, ,6;③0, ,4
如果在a与b中间插入一个数A,使a, A, b成等差数列,
那么A叫做a与b的等差中项。
思考:如果在a与b中间插入一个数A,使a, A, b成等差数列, A=?
4
6
2
四、课堂练习
1.数列{an}中,an=an+1-1,a1=2,则a5=
四、课堂练习
2.数列{an}中,2an+1=an+2+an,已知相邻三项分别为3,b,7,则b=
二、合作探究(二)
思考:如果已知一个等差数列的首项是 a1 ,公差是 d ,那么如何求出这个数列的通项an ?
二、合作探究(二)
思考:如果已知一个等差数列的首项是 a1 ,公差是 d ,那么如何求出这个数列的通项an ?
三、例题讲解
例1 (1) 已知等差数列{an}的通项公式为an=5-2n,求{an}公差和首项;
(2) 求等差数列 8,5,2,···的第20项.
三、例题讲解
例1 (1) 已知等差数列{an}的通项公式为an=5-2n,求{an}公差和首项;
(2) 求等差数列 8,5,2,···的第20项.
三、例题讲解
例2 -401是不是等差数列 -5,-9,-13,…的项?如果是,是第几项?
四、课堂练习
四、课堂练习
四、课堂练习
五、课堂小结
等差数列定义:
一般地,如果一个数列从第2项起,每一项与前一项的差都等于同一个常数,就称这个数列为等差数列,这个常数就称为等差数列的公差,用d来表示。
如果在a与b中间插入一个数A,使a, A, b成等差数列,
那么A叫做a与b的。
等差中项:
等差数通项公式:
六、作业
THANKS
