北师大版五年级下册数学3.7 倒数(课件)(共22张PPT)
文档属性
| 名称 | 北师大版五年级下册数学3.7 倒数(课件)(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 00:00:00 | ||
图片预览




文档简介
(共22张PPT)
第三单元 分数乘法
倒数
北师大版五年级下册数学课件
经历倒数的发现过程,理解倒数的意义,渗透“归纳”思想。
会求一个数(0除外)的倒数,并能解决有关倒数的问题。
在探究过程中,培养观察、分析、归纳的能力,培养数感及推理意识,激发探索数学知识的兴趣。
算一算,说一说你有什么发现。
×
2
―
3
3
―
2
=
1
×
2
1
―
2
=
1
×
7
―
9
9
―
7
=
1
×
1
―
10
10
=
1
×
7
1
―
7
×
6
―
5
5
―
6
=
1
=
1
计算结果都是1
算一算,说一说你有什么发现。
×
2
―
3
3
―
2
=
1
×
2
1
―
2
=
1
×
7
―
9
9
―
7
=
1
×
1
―
10
=
1
×
1
―
7
×
6
―
5
5
―
6
=
1
=
1
两个乘数的分子和分母交换了位置
2
―
1
10
―
1
10
7
7
―
1
乘积为1的两个数互为倒数
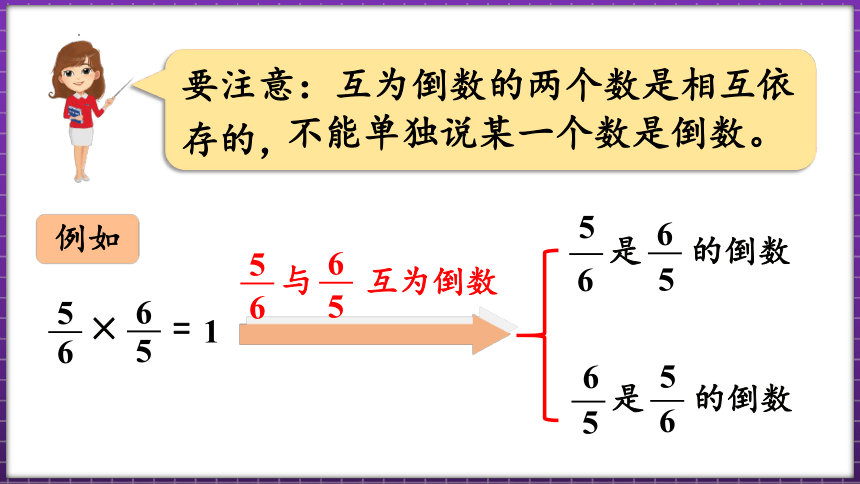
要注意:互为倒数的两个数是相互依存的,
例如
×
=
1
5
6
6
5
与
互为倒数
5
6
6
5
是
的倒数
5
6
6
5
是
的倒数
5
6
6
5
不能单独说某一个数是倒数。
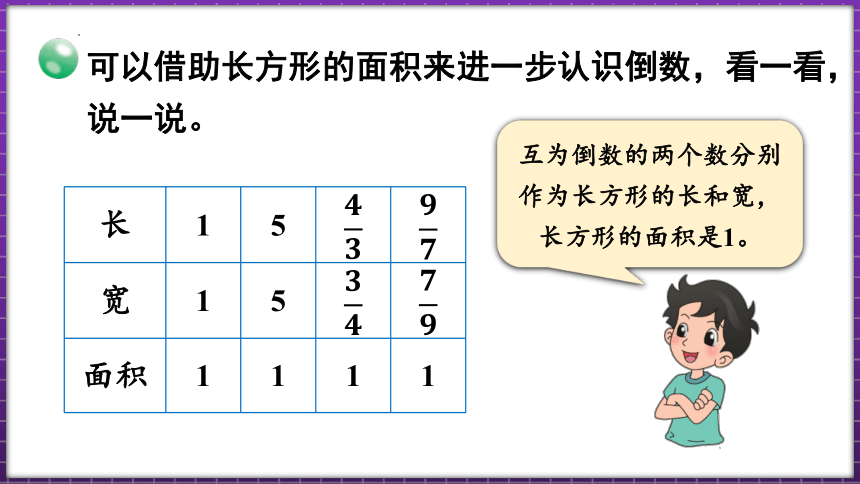
可以借助长方形的面积来进一步认识倒数,看一看,说一说。
长 1 5
宽 1 5
面积 1 1 1 1
互为倒数的两个数分别作为长方形的长和宽,长方形的面积是1。
( )
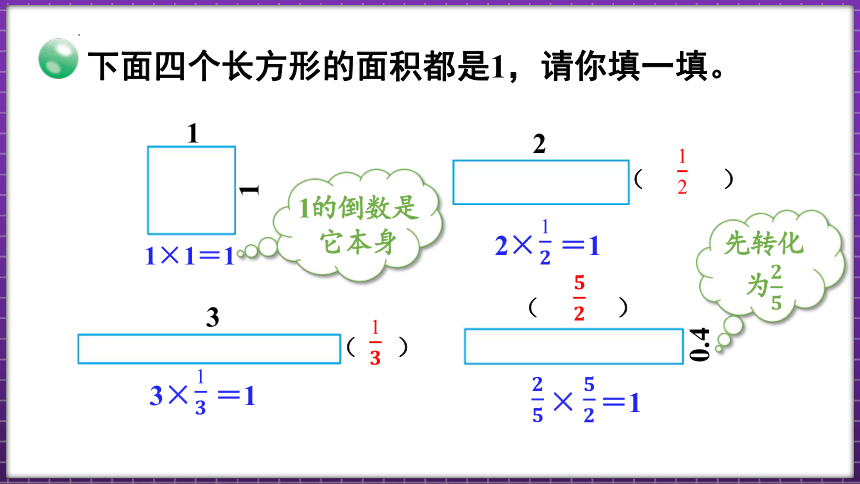
下面四个长方形的面积都是1,请你填一填。
1
1
2
1×1=1
3
( )
0.4
3× =1
( )
1的倒数是
它本身
2× =1
先转化为
× =1
1
2
3
4
…
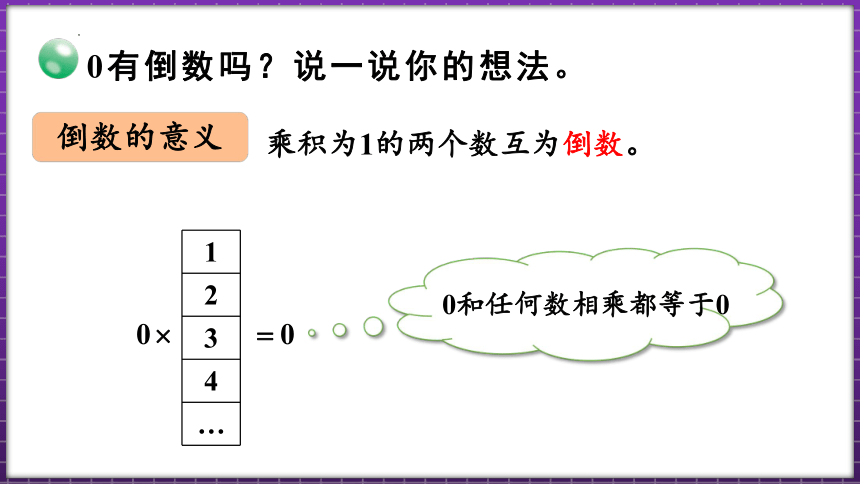
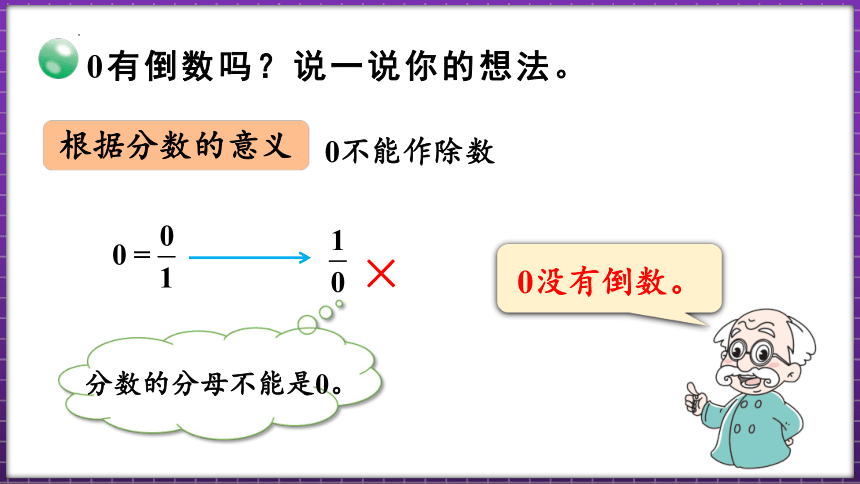
0有倒数吗?说一说你的想法。
倒数的意义
0和任何数相乘都等于0
乘积为1的两个数互为倒数。
分数的分母不能是0。
0有倒数吗?说一说你的想法。
根据分数的意义
0不能作除数
0没有倒数。
×
想一想,怎样求一个数的倒数?
分数
3
5
7
2
交换分子和分母的位置
互为倒数的两个数交换了分子和分母的位置,所以分子与分母交换位置就可以得到原数的倒数。
5
3
7
交换分子和分母的位置
2
求一个分数的倒数,只要把这个分数的分子、分母交换位置就可以了。
整数
7
1
交换分子和分母的位置
1
7
交换分子和分母的位置
1
3
3
1
3
化成分母是1的分数
7
化成分母是1的分数
求一个整数的倒数,先把整数化成分母是1的分数,再交换分子和分母的位置。
小数
交换分子和分母的位置
5
3
交换分子和分母的位置
2
2
5
转化为分数
0.6
转化为分数
0.4
5
3
5
求一个小数的倒数,先把小数转化为分数,再交换分子和分母的位置。
把互为倒数的两个数连起来。
1.
3
10
7
1
1
1
8
13
13
8
(答案不唯一)
填一填。
2.
两个数的乘积为1,这两个数互为倒数。
长和宽互为倒数。
下面长方形的面积都是 1,填一填。
3.
( )
①
3
②
( )
解:
直接写出得数。
4.
x = 1
4x = 1
x = 1
1+ x = 0
x =
解:
x =
解:
x =
解:
x = 0
<
在 里填上“>”“<”或“=”。
5.
<
=
看一看,想一想“1=?”,你还能写出不同的算式吗?
6.
1=2.5-1.5
1= +
1=7÷7
1= ×
分子是1的分数,它的倒数是整数 。
先说出下面每组数的倒数,再说一说你发现了什么规律
7.
5
6
7
8
大于1的假分数的倒数一定小于1。
先说出下面每组数的倒数,再说一说你发现了什么规律
7.
汉字里面有一些类似的互为“倒数”的字,即一个字的上、下两部分交换后,就变成了另一个字,比如:
吴 吞 杏 呆
音 昱 旮 旯
你知道吗?
同学们,这节课你们学会了哪些知识?
倒数的意义:乘积是1的两个数互为倒数。
1
求一个数倒数的方法:先化成分数,再交换这个数分子和分母的位置即可。
2
第三单元 分数乘法
倒数
北师大版五年级下册数学课件
经历倒数的发现过程,理解倒数的意义,渗透“归纳”思想。
会求一个数(0除外)的倒数,并能解决有关倒数的问题。
在探究过程中,培养观察、分析、归纳的能力,培养数感及推理意识,激发探索数学知识的兴趣。
算一算,说一说你有什么发现。
×
2
―
3
3
―
2
=
1
×
2
1
―
2
=
1
×
7
―
9
9
―
7
=
1
×
1
―
10
10
=
1
×
7
1
―
7
×
6
―
5
5
―
6
=
1
=
1
计算结果都是1
算一算,说一说你有什么发现。
×
2
―
3
3
―
2
=
1
×
2
1
―
2
=
1
×
7
―
9
9
―
7
=
1
×
1
―
10
=
1
×
1
―
7
×
6
―
5
5
―
6
=
1
=
1
两个乘数的分子和分母交换了位置
2
―
1
10
―
1
10
7
7
―
1
乘积为1的两个数互为倒数
要注意:互为倒数的两个数是相互依存的,
例如
×
=
1
5
6
6
5
与
互为倒数
5
6
6
5
是
的倒数
5
6
6
5
是
的倒数
5
6
6
5
不能单独说某一个数是倒数。
可以借助长方形的面积来进一步认识倒数,看一看,说一说。
长 1 5
宽 1 5
面积 1 1 1 1
互为倒数的两个数分别作为长方形的长和宽,长方形的面积是1。
( )
下面四个长方形的面积都是1,请你填一填。
1
1
2
1×1=1
3
( )
0.4
3× =1
( )
1的倒数是
它本身
2× =1
先转化为
× =1
1
2
3
4
…
0有倒数吗?说一说你的想法。
倒数的意义
0和任何数相乘都等于0
乘积为1的两个数互为倒数。
分数的分母不能是0。
0有倒数吗?说一说你的想法。
根据分数的意义
0不能作除数
0没有倒数。
×
想一想,怎样求一个数的倒数?
分数
3
5
7
2
交换分子和分母的位置
互为倒数的两个数交换了分子和分母的位置,所以分子与分母交换位置就可以得到原数的倒数。
5
3
7
交换分子和分母的位置
2
求一个分数的倒数,只要把这个分数的分子、分母交换位置就可以了。
整数
7
1
交换分子和分母的位置
1
7
交换分子和分母的位置
1
3
3
1
3
化成分母是1的分数
7
化成分母是1的分数
求一个整数的倒数,先把整数化成分母是1的分数,再交换分子和分母的位置。
小数
交换分子和分母的位置
5
3
交换分子和分母的位置
2
2
5
转化为分数
0.6
转化为分数
0.4
5
3
5
求一个小数的倒数,先把小数转化为分数,再交换分子和分母的位置。
把互为倒数的两个数连起来。
1.
3
10
7
1
1
1
8
13
13
8
(答案不唯一)
填一填。
2.
两个数的乘积为1,这两个数互为倒数。
长和宽互为倒数。
下面长方形的面积都是 1,填一填。
3.
( )
①
3
②
( )
解:
直接写出得数。
4.
x = 1
4x = 1
x = 1
1+ x = 0
x =
解:
x =
解:
x =
解:
x = 0
<
在 里填上“>”“<”或“=”。
5.
<
=
看一看,想一想“1=?”,你还能写出不同的算式吗?
6.
1=2.5-1.5
1= +
1=7÷7
1= ×
分子是1的分数,它的倒数是整数 。
先说出下面每组数的倒数,再说一说你发现了什么规律
7.
5
6
7
8
大于1的假分数的倒数一定小于1。
先说出下面每组数的倒数,再说一说你发现了什么规律
7.
汉字里面有一些类似的互为“倒数”的字,即一个字的上、下两部分交换后,就变成了另一个字,比如:
吴 吞 杏 呆
音 昱 旮 旯
你知道吗?
同学们,这节课你们学会了哪些知识?
倒数的意义:乘积是1的两个数互为倒数。
1
求一个数倒数的方法:先化成分数,再交换这个数分子和分母的位置即可。
2
