北师大版六年级下册数学数学好玩 神奇的莫比乌斯带 课件(25张ppt)
文档属性
| 名称 | 北师大版六年级下册数学数学好玩 神奇的莫比乌斯带 课件(25张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 11:33:10 | ||
图片预览






文档简介
(共25张PPT)
数学好玩
神奇的莫比乌斯带
北师大版六年级下册数学课件
认识“莫比乌斯带”,学会将长方形纸条制成莫比乌斯带。
通过思考操作发现并验证“莫比乌斯带”的特征,培养学生大胆猜测、勇于探究的求索精神。
在莫比乌斯带魔术般的变化中感受数学的无穷魅力,拓展数学视野,进一步激发学生学习数学的兴趣,培养学生良好的数学情感。
小资料:
德国有一位数学家叫莫比乌斯,1858年,一次偶然的机会,他发现了这样一个奇妙的纸圈。所以,人们就把这样的纸圈叫莫比乌斯圈。
对于这样一个看来十分简单的问题,数百年间,曾有许多科学家进行了认真研究,但是都没有成功。后来,德国的数学家莫比乌斯对此发生了浓厚兴趣。
有一天,他被这个问题弄得头昏脑涨了,便到野外去散步。一片片肥大的玉米叶子,令他不由自主地蹲下来,仔细观察着。叶子弯曲着耸拉下来,有许多扭成半圆形的,他认真思考着,最后撕下其中一片,顺着叶子自然扭的方向对接成一个圆圈儿,他惊喜地发现,这就是他梦寐以求的那种圈。
莫比乌斯回到办公室,裁出纸条,把纸的一端扭转180°,再将一端的正面和背面粘在一起,这样就做成了只有一个面的纸圈儿。
这张纸条有几个面、几条边?
这张纸条有两个面、4条边。
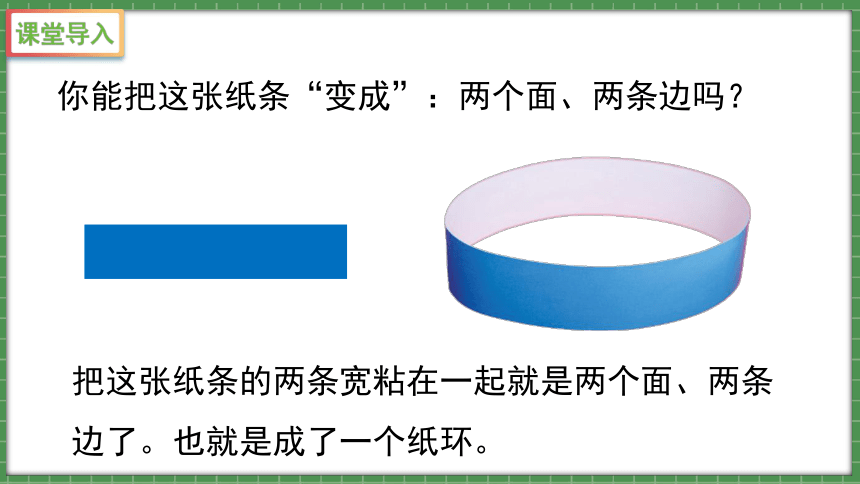
你能把这张纸条“变成”:两个面、两条边吗?
把这张纸条的两条宽粘在一起就是两个面、两条边了。也就是成了一个纸环。
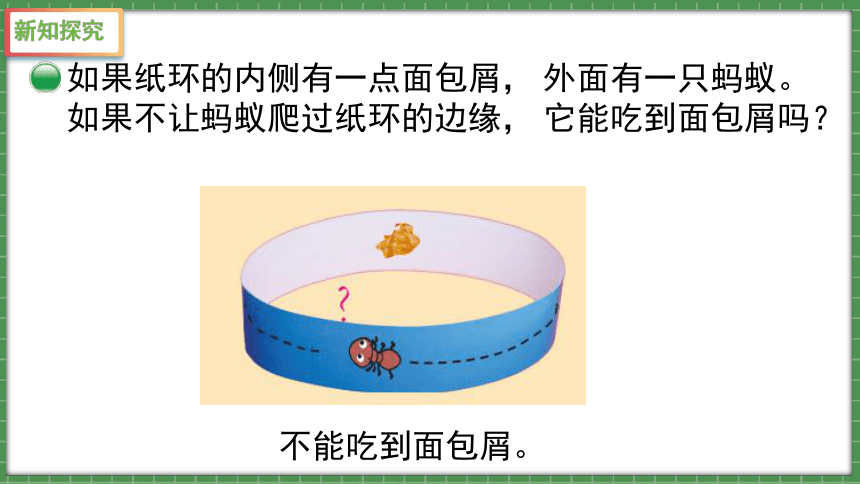
如果纸环的内侧有一点面包屑, 外面有一只蚂蚁。 如果不让蚂蚁爬过纸环的边缘, 它能吃到面包屑吗?
不能吃到面包屑。
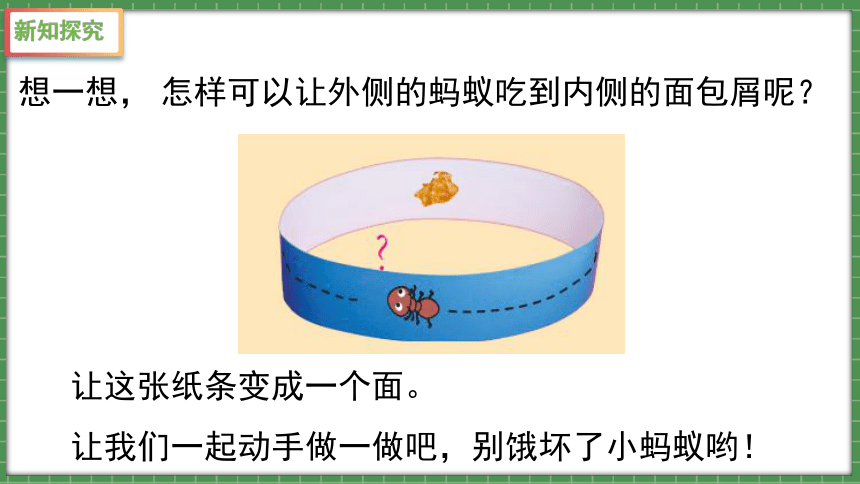
想一想, 怎样可以让外侧的蚂蚁吃到内侧的面包屑呢?
让这张纸条变成一个面。
让我们一起动手做一做吧,别饿坏了小蚂蚁哟!
(1)先用一张长方形纸条如下图那样扭一下,(也就是捏着一端,另一端扭转180° )。
(2)再把两端粘上,得到如下图的纸环。
我发现, 不管面包屑标在什么地方, 小蚂蚁都不必爬过边缘就能吃到它, 真有趣!这真是一个“神奇的纸环”!
在这个纸环上作个标记表示面包屑, 想一想, 小蚂蚁从点 A 出发能吃到面包屑吗?
分别在普通纸环和“神奇的纸环” 上各取一点。 从这点开始涂色, 不能翻过边缘一直涂下去, 你发现了什么?
“神奇的纸环”上的颜色……
普通纸环上的颜色总是只涂了一面……
再取两张长方形纸条, 每张长方形纸条中间画一条虚线(如图) , 再分别做成一个普通纸环和一个“神奇的纸环” 。 用剪刀沿纸条上的虚线剪开,你又发现了什么?
这个“神奇的纸环”叫“莫比乌斯带”,它是用数学家莫比乌斯的姓命名的。
我想把纸条平均分成三份、 四份……也做成“神奇的纸环” ,再沿虚线剪开……
沿莫比乌斯带三等分划线,然后剪开,先想一想会是什么样的呢?然后再动手操作。
沿划线剪开,得到一条比原来的莫比乌斯带空间大一倍的带和一条与原来同大小的带,二条带套在一起。
沿莫比乌斯带四等分划线。
沿划线剪开,得到二条比原来的莫比乌斯带空间大一倍的带,二条带套在一起。
沿莫比乌斯带五等分划线。
沿划线剪开,得到二条比原来的莫比乌斯带空间大一倍的带和一条与原来同大小的带,三条带套在一起。
生活中的莫比乌斯带
北京的中国科学技术馆大厅中一座“三叶纽结”模型,以向观众展示人们对数学分科拓扑学等方面探索的无限兴趣。
三叶扭结:中国科技馆的标志性的物体,是由莫比乌斯带演变而成的。
哈萨克斯坦新标志性建筑:全新国家图书馆
数学好玩
神奇的莫比乌斯带
北师大版六年级下册数学课件
认识“莫比乌斯带”,学会将长方形纸条制成莫比乌斯带。
通过思考操作发现并验证“莫比乌斯带”的特征,培养学生大胆猜测、勇于探究的求索精神。
在莫比乌斯带魔术般的变化中感受数学的无穷魅力,拓展数学视野,进一步激发学生学习数学的兴趣,培养学生良好的数学情感。
小资料:
德国有一位数学家叫莫比乌斯,1858年,一次偶然的机会,他发现了这样一个奇妙的纸圈。所以,人们就把这样的纸圈叫莫比乌斯圈。
对于这样一个看来十分简单的问题,数百年间,曾有许多科学家进行了认真研究,但是都没有成功。后来,德国的数学家莫比乌斯对此发生了浓厚兴趣。
有一天,他被这个问题弄得头昏脑涨了,便到野外去散步。一片片肥大的玉米叶子,令他不由自主地蹲下来,仔细观察着。叶子弯曲着耸拉下来,有许多扭成半圆形的,他认真思考着,最后撕下其中一片,顺着叶子自然扭的方向对接成一个圆圈儿,他惊喜地发现,这就是他梦寐以求的那种圈。
莫比乌斯回到办公室,裁出纸条,把纸的一端扭转180°,再将一端的正面和背面粘在一起,这样就做成了只有一个面的纸圈儿。
这张纸条有几个面、几条边?
这张纸条有两个面、4条边。
你能把这张纸条“变成”:两个面、两条边吗?
把这张纸条的两条宽粘在一起就是两个面、两条边了。也就是成了一个纸环。
如果纸环的内侧有一点面包屑, 外面有一只蚂蚁。 如果不让蚂蚁爬过纸环的边缘, 它能吃到面包屑吗?
不能吃到面包屑。
想一想, 怎样可以让外侧的蚂蚁吃到内侧的面包屑呢?
让这张纸条变成一个面。
让我们一起动手做一做吧,别饿坏了小蚂蚁哟!
(1)先用一张长方形纸条如下图那样扭一下,(也就是捏着一端,另一端扭转180° )。
(2)再把两端粘上,得到如下图的纸环。
我发现, 不管面包屑标在什么地方, 小蚂蚁都不必爬过边缘就能吃到它, 真有趣!这真是一个“神奇的纸环”!
在这个纸环上作个标记表示面包屑, 想一想, 小蚂蚁从点 A 出发能吃到面包屑吗?
分别在普通纸环和“神奇的纸环” 上各取一点。 从这点开始涂色, 不能翻过边缘一直涂下去, 你发现了什么?
“神奇的纸环”上的颜色……
普通纸环上的颜色总是只涂了一面……
再取两张长方形纸条, 每张长方形纸条中间画一条虚线(如图) , 再分别做成一个普通纸环和一个“神奇的纸环” 。 用剪刀沿纸条上的虚线剪开,你又发现了什么?
这个“神奇的纸环”叫“莫比乌斯带”,它是用数学家莫比乌斯的姓命名的。
我想把纸条平均分成三份、 四份……也做成“神奇的纸环” ,再沿虚线剪开……
沿莫比乌斯带三等分划线,然后剪开,先想一想会是什么样的呢?然后再动手操作。
沿划线剪开,得到一条比原来的莫比乌斯带空间大一倍的带和一条与原来同大小的带,二条带套在一起。
沿莫比乌斯带四等分划线。
沿划线剪开,得到二条比原来的莫比乌斯带空间大一倍的带,二条带套在一起。
沿莫比乌斯带五等分划线。
沿划线剪开,得到二条比原来的莫比乌斯带空间大一倍的带和一条与原来同大小的带,三条带套在一起。
生活中的莫比乌斯带
北京的中国科学技术馆大厅中一座“三叶纽结”模型,以向观众展示人们对数学分科拓扑学等方面探索的无限兴趣。
三叶扭结:中国科技馆的标志性的物体,是由莫比乌斯带演变而成的。
哈萨克斯坦新标志性建筑:全新国家图书馆
