25.2 三视图 第2课时 三视图的应用课件(共20张PPT) 沪科版九年级下册数学
文档属性
| 名称 | 25.2 三视图 第2课时 三视图的应用课件(共20张PPT) 沪科版九年级下册数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 911.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 11:36:21 | ||
图片预览








文档简介
(共20张PPT)
第25章 投影与视图
25.2 三视图
第2课时 三视图的应用
1.能根据三视图还原立体图形,回顾立体图形的侧面展开图.
2.知道棱柱的相关概念
3.能根据三视图中的数据求实物几何体的表面积和侧面积.
◎重点:棱柱的三视图与相关概念.
◎难点:几何体的相关计算.
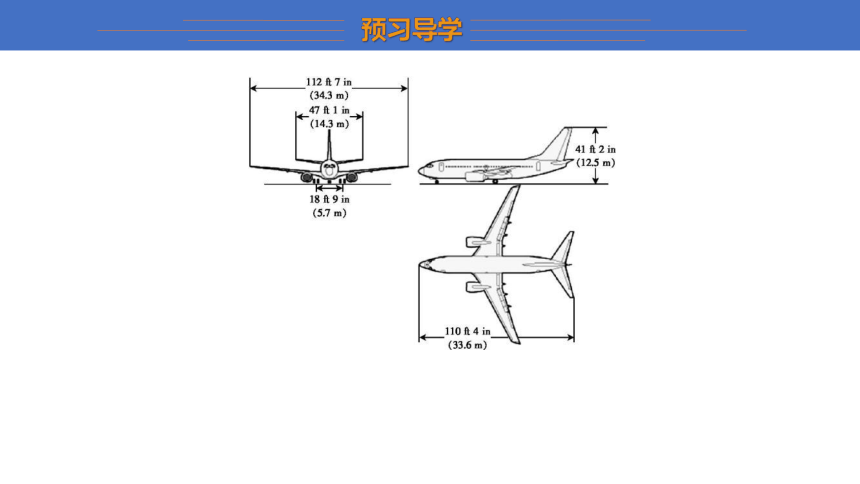
下图是一架飞机的设计图,同学们,你们能根据这三个图片想象出飞机的样子吗?飞机的翼展、高度、长度能从下面的图中得到吗?这节课,我们就来学习如何从三视图中获取几何体的相关信息.
棱柱的相关概念
阅读课本本课时“例2”前的内容,回答下列问题.
1.“图25-8(1)”中的三视图是哪个图形的三视图?
三棱柱的三视图.
2.一个几何体的三视图是唯一的,但通过视图建立起来的几何体是否也是唯一的?
不是唯一的,它有多种可能性.例如:正方体的主视图是正方形,但主视图是正方形的几何体还有直三棱柱、长方体、圆柱等.
3.什么是直棱柱?什么是正棱柱?
当侧棱垂直于底面时,棱柱称为直棱柱,直棱柱的各个侧面都是矩形.底面是正多边形的直棱柱叫做正棱柱.
由三视图计算几何体的体积和表面积
阅读课本本课时“例2”,回答下列问题.
1.将三视图转化为几何体时,一般是先利用 俯视图 (反映物体的 长 和 宽 )确定几何体的 底面形状 ,再结合 主视图 (反映物体的长和高)和 左视图 (反映物体的高和宽)确定几何体的整体形状和大小;
俯视图
长
宽
底面形状
主视图
左视图
2.立体图形沿某条边剪开后得到的平面图形叫做立体图形的 表面展开图 ,展开图 不是 唯一的.
表面展开图
不是
·导学建议·
让学生对比三视图,观察原立体图形,使学生既能根据立体图形作出其三视图,又能根据三视图想象原立体图形.对于求几何体的表面积的问题,可借助于几何体的表面展开图.
1.在下面四个几何体中,从上面看是圆形,从左面看是长方形的几何体是 ( A )
A
2.已知某物体的三视图如图所示,那么与它对应的物体是 ( C )
A B C D
C
3.一张桌子摆放若干碟子,从三个方向上看,三种视图如下图所示,则这张桌子上共有 12 个碟子.
12
将三视图转化为几何体
1.若一个几何体的三视图都是正方形,则这个几何体是 ( B )
A.长方体 B.正方体
C.圆柱 D.圆锥
B
方法归纳交流 掌握一些简单几何体的三视图,如:正方体、长方体、三棱柱、四棱柱、三棱锥、四棱锥、圆柱、圆锥、圆台和球,有助于理解简单几何图形的组合形式.
根据三视图计算实物的表面积
2.某工厂要加工一批密封罐,设计者给出了密封罐的三视图(如下图),请你按照该三视图确定制作每个密封罐所需钢板的面积.(单位:mm)
解:由三视图可知,该密封罐的形状是正六棱柱(如图1).密封罐的高为50 mm,底面正六边形的直径为100 mm.边长为50 mm,图2是它的展开图.
由展开图可知,制作一个该密封罐所需钢板的面积为6×50×50+2×6××50×50 sin 60°
=6×502×
≈27990(mm2).
方法归纳交流 计算几何体的表面积,应先画出几何体的表面展开图,然后根据三视图中的数据计算.
1.如图,这是一个工件的三视图,图中标有尺寸,则这个工件的体积是 ( B )
A.13π cm3 B.17π cm3
C.66π cm3 D.68π cm3
B
2.一个几何体的三视图如图所示,则这个几何体是 ( D )
D
3.如图,这是某几何体的主视图和俯视图,求它的表面积和体积.
解:几何体的下面是一个圆柱,上面是一个圆锥.
圆锥的母线长为=50,
底面圆的周长为60π,
∴圆锥的侧面积为×60π×50=1500π,
圆锥的底面积为π×302=900π,
圆柱的侧面积为2π×15×20=600π,
∴几何体的表面积为1500π+900π+600π=3000π.
几何体的体积为π152×20+π×302×40=16500π.
第25章 投影与视图
25.2 三视图
第2课时 三视图的应用
1.能根据三视图还原立体图形,回顾立体图形的侧面展开图.
2.知道棱柱的相关概念
3.能根据三视图中的数据求实物几何体的表面积和侧面积.
◎重点:棱柱的三视图与相关概念.
◎难点:几何体的相关计算.
下图是一架飞机的设计图,同学们,你们能根据这三个图片想象出飞机的样子吗?飞机的翼展、高度、长度能从下面的图中得到吗?这节课,我们就来学习如何从三视图中获取几何体的相关信息.
棱柱的相关概念
阅读课本本课时“例2”前的内容,回答下列问题.
1.“图25-8(1)”中的三视图是哪个图形的三视图?
三棱柱的三视图.
2.一个几何体的三视图是唯一的,但通过视图建立起来的几何体是否也是唯一的?
不是唯一的,它有多种可能性.例如:正方体的主视图是正方形,但主视图是正方形的几何体还有直三棱柱、长方体、圆柱等.
3.什么是直棱柱?什么是正棱柱?
当侧棱垂直于底面时,棱柱称为直棱柱,直棱柱的各个侧面都是矩形.底面是正多边形的直棱柱叫做正棱柱.
由三视图计算几何体的体积和表面积
阅读课本本课时“例2”,回答下列问题.
1.将三视图转化为几何体时,一般是先利用 俯视图 (反映物体的 长 和 宽 )确定几何体的 底面形状 ,再结合 主视图 (反映物体的长和高)和 左视图 (反映物体的高和宽)确定几何体的整体形状和大小;
俯视图
长
宽
底面形状
主视图
左视图
2.立体图形沿某条边剪开后得到的平面图形叫做立体图形的 表面展开图 ,展开图 不是 唯一的.
表面展开图
不是
·导学建议·
让学生对比三视图,观察原立体图形,使学生既能根据立体图形作出其三视图,又能根据三视图想象原立体图形.对于求几何体的表面积的问题,可借助于几何体的表面展开图.
1.在下面四个几何体中,从上面看是圆形,从左面看是长方形的几何体是 ( A )
A
2.已知某物体的三视图如图所示,那么与它对应的物体是 ( C )
A B C D
C
3.一张桌子摆放若干碟子,从三个方向上看,三种视图如下图所示,则这张桌子上共有 12 个碟子.
12
将三视图转化为几何体
1.若一个几何体的三视图都是正方形,则这个几何体是 ( B )
A.长方体 B.正方体
C.圆柱 D.圆锥
B
方法归纳交流 掌握一些简单几何体的三视图,如:正方体、长方体、三棱柱、四棱柱、三棱锥、四棱锥、圆柱、圆锥、圆台和球,有助于理解简单几何图形的组合形式.
根据三视图计算实物的表面积
2.某工厂要加工一批密封罐,设计者给出了密封罐的三视图(如下图),请你按照该三视图确定制作每个密封罐所需钢板的面积.(单位:mm)
解:由三视图可知,该密封罐的形状是正六棱柱(如图1).密封罐的高为50 mm,底面正六边形的直径为100 mm.边长为50 mm,图2是它的展开图.
由展开图可知,制作一个该密封罐所需钢板的面积为6×50×50+2×6××50×50 sin 60°
=6×502×
≈27990(mm2).
方法归纳交流 计算几何体的表面积,应先画出几何体的表面展开图,然后根据三视图中的数据计算.
1.如图,这是一个工件的三视图,图中标有尺寸,则这个工件的体积是 ( B )
A.13π cm3 B.17π cm3
C.66π cm3 D.68π cm3
B
2.一个几何体的三视图如图所示,则这个几何体是 ( D )
D
3.如图,这是某几何体的主视图和俯视图,求它的表面积和体积.
解:几何体的下面是一个圆柱,上面是一个圆锥.
圆锥的母线长为=50,
底面圆的周长为60π,
∴圆锥的侧面积为×60π×50=1500π,
圆锥的底面积为π×302=900π,
圆柱的侧面积为2π×15×20=600π,
∴几何体的表面积为1500π+900π+600π=3000π.
几何体的体积为π152×20+π×302×40=16500π.
