13.3.1 等腰三角形 课件 (共14张PPT) 人教版数学八年级上册
文档属性
| 名称 | 13.3.1 等腰三角形 课件 (共14张PPT) 人教版数学八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 00:00:00 | ||
图片预览





文档简介
(共14张PPT)
练习1:如下图,把一张长方形的纸片沿虚线对折,并剪去蓝色阴影部分,再把它展开,得到的△ABC有什么特点?
两腰的夹角叫做______,
①上述过程中,剪刀剪过的两条边是相等的,即△ABC中,AB=AC. 所以 △ABC是___________。
②等腰三角形中,相等的两边都叫做___,
另一边叫做_______,
腰和底边的夹角叫做______。
等腰三角形
腰
底边
底角
顶角
一、新课导入
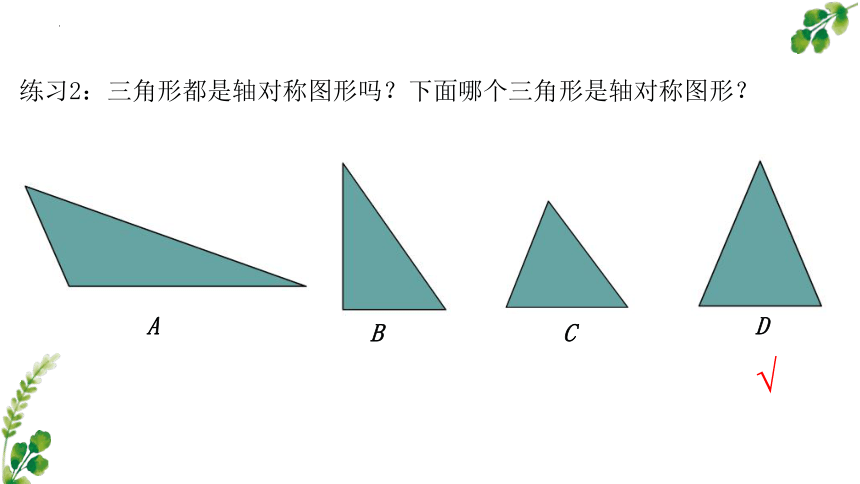
练习2:三角形都是轴对称图形吗?下面哪个三角形是轴对称图形?
C
D
B
A
√
13.3.1等腰三角形
二、学习目标:
1.理解并掌握等腰三角形的性质.
2.经历等腰三角形的性质的探究过程,能初步运用等腰三角形的性质解决有关问题.
三、重点、难点:
重点:理解并掌握等腰三角形的性质.
难点:经历等腰三角形的性质的探究过程,能初步运用等腰三角形的性质解决有关问题.
性质1:等腰三角形的两个底角相等(简写成“等边对等角”)
几何语言:∵△ABC中,AB=AC
∴ ∠B=∠C
性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简写成“三线合一”)
几何语言3:∵△ABC是等腰三角形,AD⊥BC
∴BD=CD,∠BAD=∠CAD
几何语言2:∵△ABC是等腰三角形,BD=CD
∴AD⊥BC,∠BAD=∠CAD
几何语言1:∵△ABC是等腰三角形,∠BAD=∠CAD
∴BD=CD,AD⊥BC
探究:把剪出的等腰三角形ABC沿折痕(AD所在的直线)对折,找出其中重合的线段和角.由这些重合的线段和角,你能发现等腰三角形的性质吗?说一说你的猜想.
四、◆新课讲解
(1)◆例题讲解
(2021黄山)如图,点D在AC上,AB=BD=CD,∠C=40°,求∠ABD.
解:∵AB=BD=CD
∴∠A=∠ADB,∠C=∠DBC
又∵∠C=40°
∴∠ADB=∠C+∠DBC=40°+40°=80°
∴∠ABD=180°-80°-80°=20°
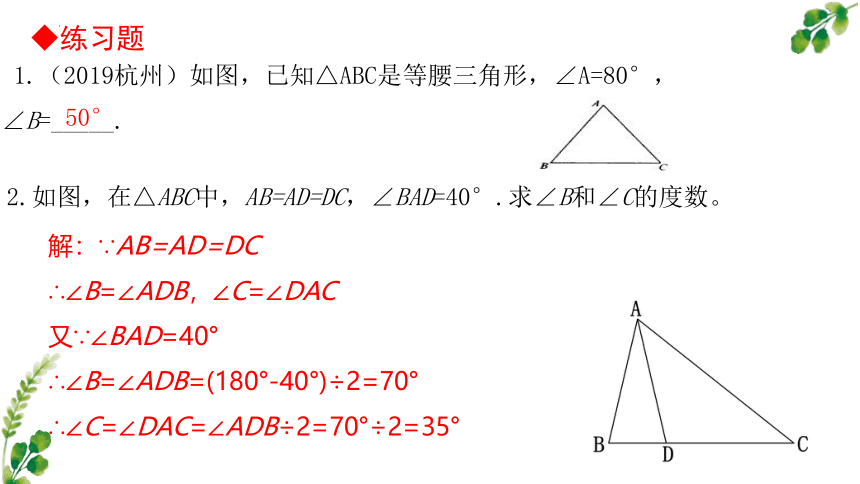
2.如图,在△ABC中,AB=AD=DC,∠BAD=40°.求∠B和∠C的度数。
解:∵AB=AD=DC
∴∠B=∠ADB,∠C=∠DAC
又∵∠BAD=40°
∴∠B=∠ADB=(180°-40°)÷2=70°
∴∠C=∠DAC=∠ADB÷2=70°÷2=35°
◆练习题
1.(2019杭州)如图,已知△ABC是等腰三角形,∠A=80°,∠B=_____.
50°
1.(2021 福建)如图,AD是等腰△ABC的顶角平分线,BD=5,求CD。
(2)◆例题讲解
解:∵AD是等腰△ABC的顶角平分线,BD=5
∴BD=CD=5(三线合一)
1.如图,在△ABC中,AB=AC,D是BC的中点,∠B=40°,则∠BAD的度数为( )
A.100° B.80° C.50° D.40°
C
◆练习题
2.如图,在△ABC中,AB=AC,AD⊥BC于点D.若AB=6,
CD=4,则△ABC的周长是_____.
20
3.已知:如图,点D、E在△ABC的边BC上,AD=AE,BD=EC.
求证: AB=AC.
◆练习题(综合运用)
证法1:
∵AD=AE
∴∠ADE=∠AED(等边对等角)
∴∠ADB=∠AEC(等角的补角相等)
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS)
∴AB=AC
3.已知:如图,点D、E在△ABC的边BC上,AD=AE,BD=EC.
求证: AB=AC.
证法2:过A作AF⊥BC于F
∵AD=AE,AF⊥BC
∴DF=EF(等腰三角形“三线合一”)
∵BD=EC
∴DF+BD=EF+EC
即BF=CF
∴AF垂直平分BC
∴AB=AC
性质1:等腰三角形的两个底角相等(简写成“等边对等角”)
性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简写成“三线合一”)
三、◆课堂小结
四、◆课后作业
见学习单P4
谢谢观看!
练习1:如下图,把一张长方形的纸片沿虚线对折,并剪去蓝色阴影部分,再把它展开,得到的△ABC有什么特点?
两腰的夹角叫做______,
①上述过程中,剪刀剪过的两条边是相等的,即△ABC中,AB=AC. 所以 △ABC是___________。
②等腰三角形中,相等的两边都叫做___,
另一边叫做_______,
腰和底边的夹角叫做______。
等腰三角形
腰
底边
底角
顶角
一、新课导入
练习2:三角形都是轴对称图形吗?下面哪个三角形是轴对称图形?
C
D
B
A
√
13.3.1等腰三角形
二、学习目标:
1.理解并掌握等腰三角形的性质.
2.经历等腰三角形的性质的探究过程,能初步运用等腰三角形的性质解决有关问题.
三、重点、难点:
重点:理解并掌握等腰三角形的性质.
难点:经历等腰三角形的性质的探究过程,能初步运用等腰三角形的性质解决有关问题.
性质1:等腰三角形的两个底角相等(简写成“等边对等角”)
几何语言:∵△ABC中,AB=AC
∴ ∠B=∠C
性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简写成“三线合一”)
几何语言3:∵△ABC是等腰三角形,AD⊥BC
∴BD=CD,∠BAD=∠CAD
几何语言2:∵△ABC是等腰三角形,BD=CD
∴AD⊥BC,∠BAD=∠CAD
几何语言1:∵△ABC是等腰三角形,∠BAD=∠CAD
∴BD=CD,AD⊥BC
探究:把剪出的等腰三角形ABC沿折痕(AD所在的直线)对折,找出其中重合的线段和角.由这些重合的线段和角,你能发现等腰三角形的性质吗?说一说你的猜想.
四、◆新课讲解
(1)◆例题讲解
(2021黄山)如图,点D在AC上,AB=BD=CD,∠C=40°,求∠ABD.
解:∵AB=BD=CD
∴∠A=∠ADB,∠C=∠DBC
又∵∠C=40°
∴∠ADB=∠C+∠DBC=40°+40°=80°
∴∠ABD=180°-80°-80°=20°
2.如图,在△ABC中,AB=AD=DC,∠BAD=40°.求∠B和∠C的度数。
解:∵AB=AD=DC
∴∠B=∠ADB,∠C=∠DAC
又∵∠BAD=40°
∴∠B=∠ADB=(180°-40°)÷2=70°
∴∠C=∠DAC=∠ADB÷2=70°÷2=35°
◆练习题
1.(2019杭州)如图,已知△ABC是等腰三角形,∠A=80°,∠B=_____.
50°
1.(2021 福建)如图,AD是等腰△ABC的顶角平分线,BD=5,求CD。
(2)◆例题讲解
解:∵AD是等腰△ABC的顶角平分线,BD=5
∴BD=CD=5(三线合一)
1.如图,在△ABC中,AB=AC,D是BC的中点,∠B=40°,则∠BAD的度数为( )
A.100° B.80° C.50° D.40°
C
◆练习题
2.如图,在△ABC中,AB=AC,AD⊥BC于点D.若AB=6,
CD=4,则△ABC的周长是_____.
20
3.已知:如图,点D、E在△ABC的边BC上,AD=AE,BD=EC.
求证: AB=AC.
◆练习题(综合运用)
证法1:
∵AD=AE
∴∠ADE=∠AED(等边对等角)
∴∠ADB=∠AEC(等角的补角相等)
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS)
∴AB=AC
3.已知:如图,点D、E在△ABC的边BC上,AD=AE,BD=EC.
求证: AB=AC.
证法2:过A作AF⊥BC于F
∵AD=AE,AF⊥BC
∴DF=EF(等腰三角形“三线合一”)
∵BD=EC
∴DF+BD=EF+EC
即BF=CF
∴AF垂直平分BC
∴AB=AC
性质1:等腰三角形的两个底角相等(简写成“等边对等角”)
性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简写成“三线合一”)
三、◆课堂小结
四、◆课后作业
见学习单P4
谢谢观看!
