13.1 三角形 第3课时 课件(共17张PPT) 青岛版七年级下册数学
文档属性
| 名称 | 13.1 三角形 第3课时 课件(共17张PPT) 青岛版七年级下册数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 12:22:28 | ||
图片预览





文档简介
(共17张PPT)
第十三章 平面图形的认识
13.1 三角形
第3课时
1.了解三角形的角平分线、中线和重心的概念并掌握其性质,并掌握三角形三条角平分线/中线交于三角形内部一点
2.认识三角形的高,能画任意三角形的高,了解三角形三条高所在直线交于一点
任务一:认识三角形的角平分线、中线和重心
活动1:想一想:下图中,如果∠1=∠2,线段AD叫做什么?
定义:在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫三角形的角平分线.
A
C
B
∠1=∠2
1
2
D
试一试:请分别画出锐角三角形、钝角三角形和直角三角形这三个三角形的三条角平分线. 在每个三角形中,这三条角平分线之间有怎样的位置关系呢
三角形的三条角平分线交三角形内部于一点
小结
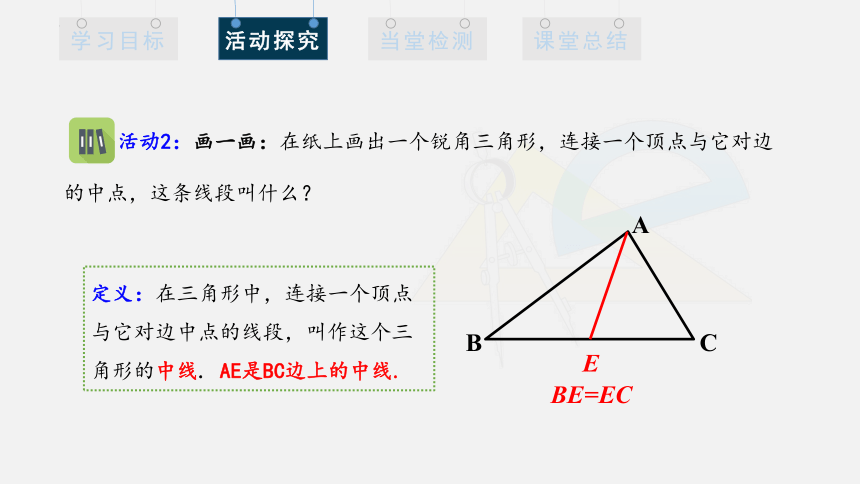
活动2:画一画:在纸上画出一个锐角三角形,连接一个顶点与它对边的中点,这条线段叫什么?
B
A
C
BE=EC
E
定义:在三角形中,连接一个顶点与它对边中点的线段,叫作这个三角形的中线. AE是BC边上的中线.
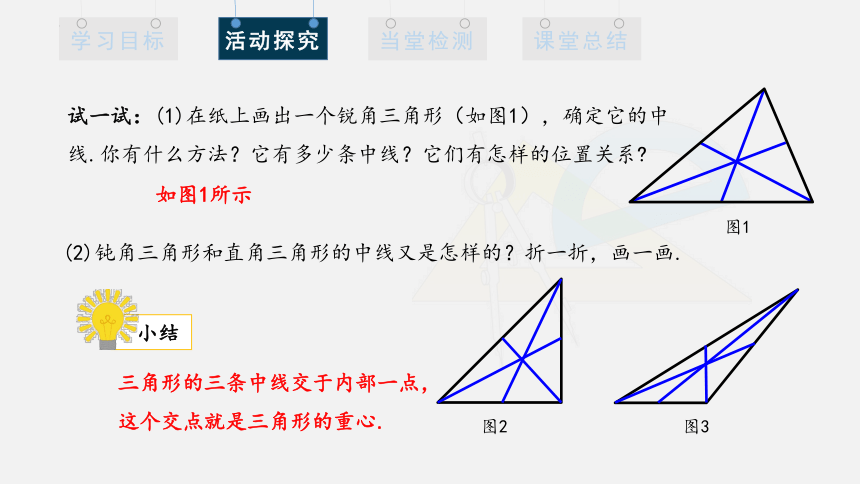
试一试:(1)在纸上画出一个锐角三角形(如图1),确定它的中线.你有什么方法?它有多少条中线?它们有怎样的位置关系
图1
(2)钝角三角形和直角三角形的中线又是怎样的?折一折,画一画.
图2
图3
如图1所示
三角形的三条中线交于内部一点,
这个交点就是三角形的重心.
小结
归纳总结
三角形
角平分线:三条角平分线交三角形内部于一点
中线:三角形的三条中线交于一点,这个交点就是三角形的重心.
练一练
下列说法中正确的是( )
A.三角形的角平分线和中线都是线段
B.三角形的角平分线和中线都是射线
C.三角形的角平分线是射线,而中线是线段
D.三角形的角平分线是线段,而中线是射线
A
任务二:认识三角形的高
活动1:画一画:过去我们学习过三角形的面积公式S= ah,您能说出什么是三角形的高吗?画一个三角形你能画出它的一个顶点到对边所在直线的垂线段吗?
定义:从三角形的一个顶点,向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高线,简称三角形的高.
A
B
C
F
要标明垂直的记号和垂足的字母!
活动2:在纸上画出一个锐角三角形、一个直角三角形和一个钝角三角形,小组合作,请分别画出它们的三条高,探究它们的位置关系:
1.锐角三角形
想一想:(1)这三条高之间有怎样的位置关系?
锐角三角形的三条高交于同一点;
(2) 锐角三角形的三条高是在三角形的内部还是外部
锐角三角形的三条高都在三角形的内部.
O
A
C
B
在纸上画出一个直角三角形.
画出直角三角形的三条高它们有怎样的位置关系?
直角三角形的三条高交于直角顶点.
2.直角三角形
A
B
C
D
3.钝角三角形
想一想:钝角三角形的三条高是在三角形的内部还是外部 三条高有何位置关系?
一条在内部,两条在外部;
三条高所在直线的交点在三角形的外部.
A
B
C
F
E
D
O
归纳总结
三角形的三条高所在的直线交于一点,
①锐角三角形三条高的交点在三角形内,
②直角三角形三条高的交点在直角顶点上,
③钝角三角形三条高所在直线的交点在三角形外.
练一练
在数学课上,同学们在练习画边AC上的高时,出现下列四种图形,其中正确的是( )
C
1.下列说法正确的是 ( )
A.三角形三条高都在三角形内
B.三角形三条中线相交于一点
C.三角形的三条角平分线可能在三角形内,也可能在三角形外
D.三角形的角平分线是射线
B
2.在△ABC中,AD是边BC上的高,也是∠BAC的角平分线,若∠B=40°,求∠BAC的度数.
解:在△ABC中,因为AD是边BC上的高
所以AD⊥BC,所以∠ADB=90°
在Rt△ABD中,∠ADB=90°,∠B=40°
所以∠BAD=90°-∠B=90°-40°=50°
又因为AD是∠BAC 的角平分线
所以∠BAC=2∠BAD=100°
3.在△ABC中,CD是中线,已知BC-AC=5cm,△DBC 的周长为25cm,求△ADC的周长.
A
D
B
C
解:因为CD是△ABC的中线,所以BD=AD,
所以△DBC的周长=BC+BD+CD=25cm,
则BD+CD=25-BC.
所以△ADC的周长=AD+CD+AC=BD+CD+AC
=25-BC+AC
=25-(BC-AC)
=25-5=20cm.
说一说你本堂课都学到了哪些知识?
三角形
高:在三角形中,三条高所在直线交于一点.
角平分线:在三角形中,三条角平分线交于一点.
中线:在三角形中,三条中线交于一点,为“重心”.
第十三章 平面图形的认识
13.1 三角形
第3课时
1.了解三角形的角平分线、中线和重心的概念并掌握其性质,并掌握三角形三条角平分线/中线交于三角形内部一点
2.认识三角形的高,能画任意三角形的高,了解三角形三条高所在直线交于一点
任务一:认识三角形的角平分线、中线和重心
活动1:想一想:下图中,如果∠1=∠2,线段AD叫做什么?
定义:在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫三角形的角平分线.
A
C
B
∠1=∠2
1
2
D
试一试:请分别画出锐角三角形、钝角三角形和直角三角形这三个三角形的三条角平分线. 在每个三角形中,这三条角平分线之间有怎样的位置关系呢
三角形的三条角平分线交三角形内部于一点
小结
活动2:画一画:在纸上画出一个锐角三角形,连接一个顶点与它对边的中点,这条线段叫什么?
B
A
C
BE=EC
E
定义:在三角形中,连接一个顶点与它对边中点的线段,叫作这个三角形的中线. AE是BC边上的中线.
试一试:(1)在纸上画出一个锐角三角形(如图1),确定它的中线.你有什么方法?它有多少条中线?它们有怎样的位置关系
图1
(2)钝角三角形和直角三角形的中线又是怎样的?折一折,画一画.
图2
图3
如图1所示
三角形的三条中线交于内部一点,
这个交点就是三角形的重心.
小结
归纳总结
三角形
角平分线:三条角平分线交三角形内部于一点
中线:三角形的三条中线交于一点,这个交点就是三角形的重心.
练一练
下列说法中正确的是( )
A.三角形的角平分线和中线都是线段
B.三角形的角平分线和中线都是射线
C.三角形的角平分线是射线,而中线是线段
D.三角形的角平分线是线段,而中线是射线
A
任务二:认识三角形的高
活动1:画一画:过去我们学习过三角形的面积公式S= ah,您能说出什么是三角形的高吗?画一个三角形你能画出它的一个顶点到对边所在直线的垂线段吗?
定义:从三角形的一个顶点,向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高线,简称三角形的高.
A
B
C
F
要标明垂直的记号和垂足的字母!
活动2:在纸上画出一个锐角三角形、一个直角三角形和一个钝角三角形,小组合作,请分别画出它们的三条高,探究它们的位置关系:
1.锐角三角形
想一想:(1)这三条高之间有怎样的位置关系?
锐角三角形的三条高交于同一点;
(2) 锐角三角形的三条高是在三角形的内部还是外部
锐角三角形的三条高都在三角形的内部.
O
A
C
B
在纸上画出一个直角三角形.
画出直角三角形的三条高它们有怎样的位置关系?
直角三角形的三条高交于直角顶点.
2.直角三角形
A
B
C
D
3.钝角三角形
想一想:钝角三角形的三条高是在三角形的内部还是外部 三条高有何位置关系?
一条在内部,两条在外部;
三条高所在直线的交点在三角形的外部.
A
B
C
F
E
D
O
归纳总结
三角形的三条高所在的直线交于一点,
①锐角三角形三条高的交点在三角形内,
②直角三角形三条高的交点在直角顶点上,
③钝角三角形三条高所在直线的交点在三角形外.
练一练
在数学课上,同学们在练习画边AC上的高时,出现下列四种图形,其中正确的是( )
C
1.下列说法正确的是 ( )
A.三角形三条高都在三角形内
B.三角形三条中线相交于一点
C.三角形的三条角平分线可能在三角形内,也可能在三角形外
D.三角形的角平分线是射线
B
2.在△ABC中,AD是边BC上的高,也是∠BAC的角平分线,若∠B=40°,求∠BAC的度数.
解:在△ABC中,因为AD是边BC上的高
所以AD⊥BC,所以∠ADB=90°
在Rt△ABD中,∠ADB=90°,∠B=40°
所以∠BAD=90°-∠B=90°-40°=50°
又因为AD是∠BAC 的角平分线
所以∠BAC=2∠BAD=100°
3.在△ABC中,CD是中线,已知BC-AC=5cm,△DBC 的周长为25cm,求△ADC的周长.
A
D
B
C
解:因为CD是△ABC的中线,所以BD=AD,
所以△DBC的周长=BC+BD+CD=25cm,
则BD+CD=25-BC.
所以△ADC的周长=AD+CD+AC=BD+CD+AC
=25-BC+AC
=25-(BC-AC)
=25-5=20cm.
说一说你本堂课都学到了哪些知识?
三角形
高:在三角形中,三条高所在直线交于一点.
角平分线:在三角形中,三条角平分线交于一点.
中线:在三角形中,三条中线交于一点,为“重心”.
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
