九年级数学下册试题 6.6图形的位似-苏科版(含答案)
文档属性
| 名称 | 九年级数学下册试题 6.6图形的位似-苏科版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 268.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 12:58:27 | ||
图片预览



文档简介
6.6图形的位似
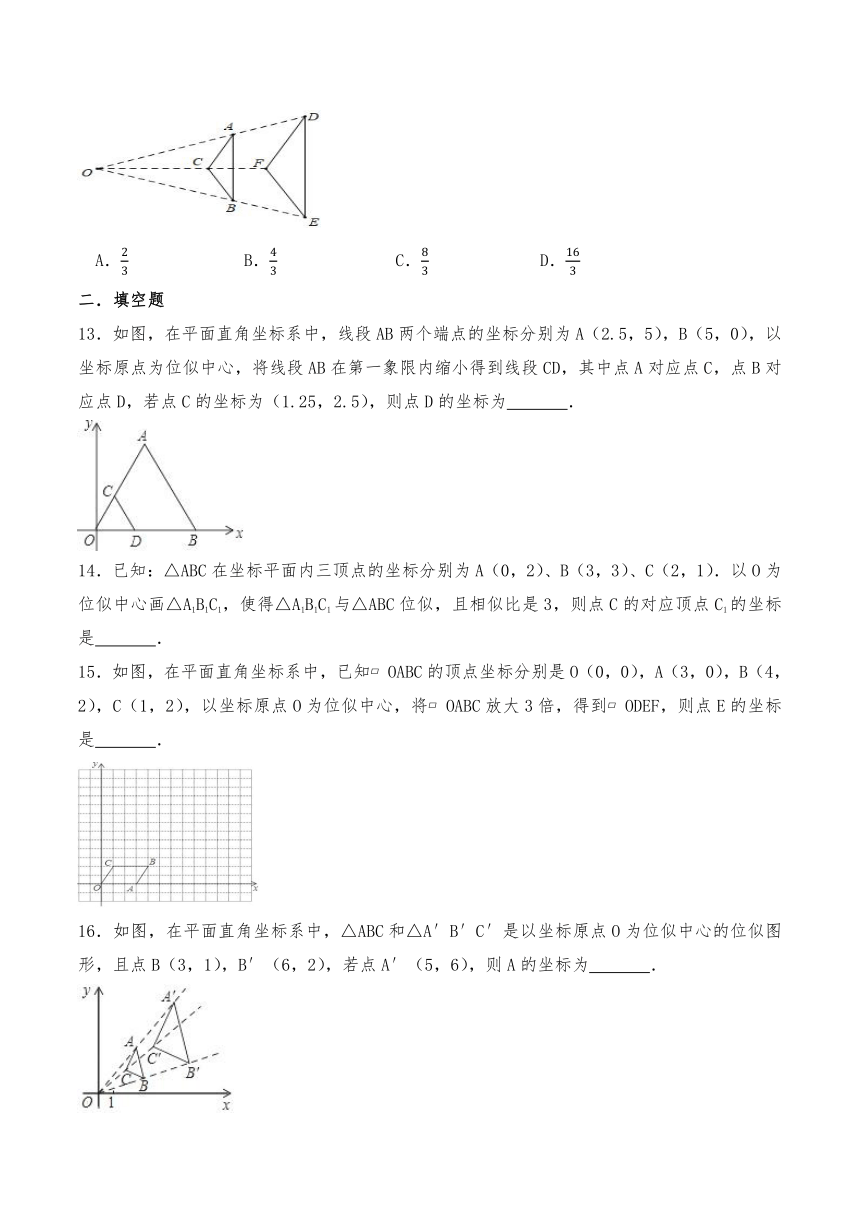
一.选择题
1.已知△ABC与△A1B1C1是关于原点为中心的位似图形,且A(2,1),△ABC与△A1B1C1的相似比为,则A的对应点A1的坐标是( )
A.(4,2) B.(﹣4,﹣2)
C.(4,2)或(﹣4,﹣2) D.(6,3)
2.如图,平面直角坐标系xOy中,点A、B的坐标分别为(9,0)、(6,﹣9),△AB'O'是△ABO关于点A的位似图形,且O'的坐标为(﹣3,0),则点B'的坐标为( )
A.(8,﹣12) B.(﹣8,12)
C.(8,﹣12)或(﹣8,12) D.(5,﹣12)
3.如图,△ABC与△DEF位似,点O为位似中心.已知OA:OD=1:2,则△ABC与△DEF的面积比为( )
A.1:2 B.1:3 C.1:4 D.1:5
4.如图,△ABC和△A1B1C1是以点O为位似中心的位似三角形,若C1为OC的中点,S3,则△ABC的面积为( )
A.15 B.12 C.9 D.6
5.如图,四边形ABCD与四边形EFGH相似,位似中心是点O,若OE=AE,则S四边形EFGH:S四边形ABCD的值是( )
A. B. C. D.
6.如图,△ABC与△DEF位似,其位似中心为点O,且OD=AD,则△ABC与△DEF的位似比是( )
A.2:1 B.4:1 C. D.
7.如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ABC的三个顶点均在格点(网格线的交点)上.以原点O为位似中心,画△A1B1C1,使它与△ABC的相似比为2,则点B的对应点B1的坐标是( )
A.(4,2) B.(1,)
C.(1,)或(﹣1,) D.(4,2)或(﹣4,﹣2)
8.如图,线段AB两个端点的坐标分别为A(1,3)、B(3,0),以原点为位似中心,将线段AB放大得到线段CD,若点C的坐标为(6,0),则点D的坐标为( )
A.(3,6) B.(2,4.5) C.(2,6) D.(1.5,4.5)
9.如图,在平面直角坐标系中,已知点A(2,4),B(4,1),以原点O为位似中心,将△OAB缩小为原来的,则点A的对应点A的坐标是( )
A.(2,) B.(1,2)
C.(4,8)或(﹣4,﹣8) D.(1,2)或(﹣1,﹣2)
10.如图,四边形ABCD与四边形EFGH位似,位似中心点是O,,则的值为( )
A. B. C. D.
11.在平面直角坐标系中,以原点O为位似中心,把△ABC放大得到△A1B1C1,使它们的相似比为1:2,若点A的坐标为(2,2),则它的对应点A1的坐标一定是( )
A.(﹣2,﹣2) B.(1,1)
C.(4,4) D.(4,4)或(﹣4,﹣4)
12.如图,△ABC与△DEF是位似图形,位似比为2:3,已知DF=4,则AC的长为( )
A. B. C. D.
二.填空题
13.如图,在平面直角坐标系中,线段AB两个端点的坐标分别为A(2.5,5),B(5,0),以坐标原点为位似中心,将线段AB在第一象限内缩小得到线段CD,其中点A对应点C,点B对应点D,若点C的坐标为(1.25,2.5),则点D的坐标为 .
14.已知:△ABC在坐标平面内三顶点的坐标分别为A(0,2)、B(3,3)、C(2,1).以O为位似中心画△A1B1C1,使得△A1B1C1与△ABC位似,且相似比是3,则点C的对应顶点C1的坐标是 .
15.如图,在平面直角坐标系中,已知 OABC的顶点坐标分别是O(0,0),A(3,0),B(4,2),C(1,2),以坐标原点O为位似中心,将 OABC放大3倍,得到 ODEF,则点E的坐标是 .
16.如图,在平面直角坐标系中,△ABC和△A′B′C′是以坐标原点O为位似中心的位似图形,且点B(3,1),B′(6,2),若点A′(5,6),则A的坐标为 .
17.如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(﹣1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C′,并把△ABC的边长放大到原来的2倍.设点B的对应点B′的坐标是(a,b),则点B的坐标是 .
18.在平面直角坐标系中,将△AOB以点O为位似中心,为位似比作位似变换,得到△A1OB1,已知A(2,3),则点A1的坐标是 .
19.在平面直角坐标系中,矩形OABC的顶点坐标分别是O(0,0),A(8,0),B(8,6),D(0,6),已知矩形OA1B1C1与矩形OABC位似,位似中心为坐标原点O,位似比为,则点B1的坐标是 .
20.如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,B的坐标是(4,2),如果以点O为位似中心,将矩形OABC缩小为原来的,那么点B的对应点B'的坐标是 .
21.如图,四边形ABCD与四边形A1B1C1D1关于点O成位似图形,若四边形ABCD与四边形A1B1C1D1的位似比为1:3,则四边形ABCD与四边形A1B1C1D1的周长比为 .
22.如图,矩形EFGO的两边在坐标轴上,点O为平面直角坐标系的原点,以y轴上的某一点为位似中心,作位似图形ABCD,且点B,F的坐标分别为(﹣4,4),(2,1),则位似中心的坐标为 .
23.△ABC与△A′B′C′是位似图形,且△ABC与△A′B′C′的位似比是1:2,已知△ABC的面积是3,则△A′B′C′的面积是 .
24.如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD,若B(1,0),则点C的坐标为 .
三.解答题
25.在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,﹣2),B(2,﹣1),C(4,﹣3).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)以点O为位似中心,在网格中画出△A1B1C1的位似图形△A2B2C2,使△A2B2C2与△A1B1C1的相似比为2:1;
(3)设点P(a,b)为△ABC内一点,则依上述两次变换后点P在△A2B2C2内的对应点P2的坐标是 .
26.如图,利用直尺、计算机或图形计算器任意画一个△ABC,以点O为位似中心,自选相似比k,进行位似变换,得到△A'B′C′.度量线段OA,OA′,OB,OB′,OC,OC′的长,你有什么发现?任意改变△ABC的位置,得出的结论是否仍然成立?
27.已知,△ABC在平面直角坐标系的位置如图所示,点A,B,C的坐标分别为(1,0),(4,﹣1),(3,2).△A1B1C1与△ABC是以点P为位似中心的位似图形.
(1)请画出点P的位置,并写出点P的坐标 ;
(2)以点O为位似中心,在y轴左侧画出△ABC的位似图形△A2B2C2,使相似比为1:1,若点M(a,b)为△ABC内一点,则点M在△A2B2C2内的对应点的坐标为 .
28.如图,已知O是坐标原点,AB两点的坐标分别为(3,﹣1),(2,1).
(1)以点O为位似中心,在y轴的左侧将△OAB放大2倍;
(2)分别写出A,B两点的对应点A',B'的坐标.
29.如图,△ABC与△DOE是位似图形,A(0,3),B(﹣2,0),C(1,0),E(6,0),△ABC与△DOE的位似中心为M.
(1)写出D点的坐标;
(2)在图中画出M点,并求M点的坐标.
30.如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(3,0),C(1,﹣1),AC交x轴于点P.
(1)∠ACB的度数为 ;
(2)P点坐标为 ;
(3)以点O为位似中心,将△ABC放大为原来的2倍,请在图中画出所有符合条件的三角形.
答案
一.选择题
C.D.C.B.B.A.D.C.D.C.D.C.
二.填空题
13.(2.5,0).
14.(6,3)或(﹣6,﹣3).
15.(12,6)或(﹣12,﹣6).
16.(2.5,3).
17.(,).
18.(,2).
19.(4,3)或(﹣4,﹣3).
20.(2,1)或(﹣2,﹣1).
21.1:3.
22.(0,2).
23.12.
24.(1,1).
三.解答题
25.解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作;
(3)点P的对应点P2的坐标是(2a,﹣2b).
故答案为(2a,﹣2b).
26.解:经测量,OA=2cm,OA′=1cm,OB=3cm,OB′=1.5cm,OC=3cm,OC′=1.5cm,
可以得到,2,
∴A′B′∥AB,A′C′∥AC,C′B′∥CB,即位似图形的对应边互相平行,
任意改变△ABC的位置,得到△A'B′C′,△ABC与△A'B′C′的对应边互相平行,
即意改变△ABC的位置,得出的结论仍然成立.
27.解:(1)如图所示:点P(0,﹣2);
(2)如图所示:△A2B2C2即为所求,点M对应点的坐标为:(﹣a,﹣b).
故答案为:(1)(0,﹣2);(2)(﹣a,﹣b).
28.解:(1)如图所示:△OA′B′,即为所求;
(2)A'的坐标是(﹣6,2),B'的坐标是(﹣4,﹣2).
29.解:(1)过点D作DH⊥OE于点H,
∵△ABC与△DOE是位似图形,A(0,3),B(﹣2,0),C(1,0),E(6,0),
∴BC=3,OE=6,△AOB∽△DHO,
∴位似比为:3:6=1:2,
∴OH=2OB=4,DH=2OA=6,
∴D点的坐标为:(4,6);
(2)连接DA并延长,交x轴于点M,则点M即为△ABC与△DOE的位似中心;
则MO:MH=1:2,
设MO=x,则MH=x+4,
∴x:(x+4)=1:2,
解得:x=4,
∴M点的坐标为(﹣4,0 ).
30.解:(1)∵∠ABC=90°,AB=CB,
∴△ABC为等腰直角三角形,
∴∠ACB=45°;
故答案为:45°;
(2)由题意得:A(2,2),C(1,﹣1),
设直线AC解析式为y=kx+b,
把A与C坐标代入得:,
解得:,即直线AC解析式为y=3x﹣4,
令y=0,得到x,
则P的坐标为(,0);
故答案为:(,0);
(3)如图所示:△A1B1C1和△A2B2C2为所求三角形.
一.选择题
1.已知△ABC与△A1B1C1是关于原点为中心的位似图形,且A(2,1),△ABC与△A1B1C1的相似比为,则A的对应点A1的坐标是( )
A.(4,2) B.(﹣4,﹣2)
C.(4,2)或(﹣4,﹣2) D.(6,3)
2.如图,平面直角坐标系xOy中,点A、B的坐标分别为(9,0)、(6,﹣9),△AB'O'是△ABO关于点A的位似图形,且O'的坐标为(﹣3,0),则点B'的坐标为( )
A.(8,﹣12) B.(﹣8,12)
C.(8,﹣12)或(﹣8,12) D.(5,﹣12)
3.如图,△ABC与△DEF位似,点O为位似中心.已知OA:OD=1:2,则△ABC与△DEF的面积比为( )
A.1:2 B.1:3 C.1:4 D.1:5
4.如图,△ABC和△A1B1C1是以点O为位似中心的位似三角形,若C1为OC的中点,S3,则△ABC的面积为( )
A.15 B.12 C.9 D.6
5.如图,四边形ABCD与四边形EFGH相似,位似中心是点O,若OE=AE,则S四边形EFGH:S四边形ABCD的值是( )
A. B. C. D.
6.如图,△ABC与△DEF位似,其位似中心为点O,且OD=AD,则△ABC与△DEF的位似比是( )
A.2:1 B.4:1 C. D.
7.如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ABC的三个顶点均在格点(网格线的交点)上.以原点O为位似中心,画△A1B1C1,使它与△ABC的相似比为2,则点B的对应点B1的坐标是( )
A.(4,2) B.(1,)
C.(1,)或(﹣1,) D.(4,2)或(﹣4,﹣2)
8.如图,线段AB两个端点的坐标分别为A(1,3)、B(3,0),以原点为位似中心,将线段AB放大得到线段CD,若点C的坐标为(6,0),则点D的坐标为( )
A.(3,6) B.(2,4.5) C.(2,6) D.(1.5,4.5)
9.如图,在平面直角坐标系中,已知点A(2,4),B(4,1),以原点O为位似中心,将△OAB缩小为原来的,则点A的对应点A的坐标是( )
A.(2,) B.(1,2)
C.(4,8)或(﹣4,﹣8) D.(1,2)或(﹣1,﹣2)
10.如图,四边形ABCD与四边形EFGH位似,位似中心点是O,,则的值为( )
A. B. C. D.
11.在平面直角坐标系中,以原点O为位似中心,把△ABC放大得到△A1B1C1,使它们的相似比为1:2,若点A的坐标为(2,2),则它的对应点A1的坐标一定是( )
A.(﹣2,﹣2) B.(1,1)
C.(4,4) D.(4,4)或(﹣4,﹣4)
12.如图,△ABC与△DEF是位似图形,位似比为2:3,已知DF=4,则AC的长为( )
A. B. C. D.
二.填空题
13.如图,在平面直角坐标系中,线段AB两个端点的坐标分别为A(2.5,5),B(5,0),以坐标原点为位似中心,将线段AB在第一象限内缩小得到线段CD,其中点A对应点C,点B对应点D,若点C的坐标为(1.25,2.5),则点D的坐标为 .
14.已知:△ABC在坐标平面内三顶点的坐标分别为A(0,2)、B(3,3)、C(2,1).以O为位似中心画△A1B1C1,使得△A1B1C1与△ABC位似,且相似比是3,则点C的对应顶点C1的坐标是 .
15.如图,在平面直角坐标系中,已知 OABC的顶点坐标分别是O(0,0),A(3,0),B(4,2),C(1,2),以坐标原点O为位似中心,将 OABC放大3倍,得到 ODEF,则点E的坐标是 .
16.如图,在平面直角坐标系中,△ABC和△A′B′C′是以坐标原点O为位似中心的位似图形,且点B(3,1),B′(6,2),若点A′(5,6),则A的坐标为 .
17.如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(﹣1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C′,并把△ABC的边长放大到原来的2倍.设点B的对应点B′的坐标是(a,b),则点B的坐标是 .
18.在平面直角坐标系中,将△AOB以点O为位似中心,为位似比作位似变换,得到△A1OB1,已知A(2,3),则点A1的坐标是 .
19.在平面直角坐标系中,矩形OABC的顶点坐标分别是O(0,0),A(8,0),B(8,6),D(0,6),已知矩形OA1B1C1与矩形OABC位似,位似中心为坐标原点O,位似比为,则点B1的坐标是 .
20.如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,B的坐标是(4,2),如果以点O为位似中心,将矩形OABC缩小为原来的,那么点B的对应点B'的坐标是 .
21.如图,四边形ABCD与四边形A1B1C1D1关于点O成位似图形,若四边形ABCD与四边形A1B1C1D1的位似比为1:3,则四边形ABCD与四边形A1B1C1D1的周长比为 .
22.如图,矩形EFGO的两边在坐标轴上,点O为平面直角坐标系的原点,以y轴上的某一点为位似中心,作位似图形ABCD,且点B,F的坐标分别为(﹣4,4),(2,1),则位似中心的坐标为 .
23.△ABC与△A′B′C′是位似图形,且△ABC与△A′B′C′的位似比是1:2,已知△ABC的面积是3,则△A′B′C′的面积是 .
24.如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD,若B(1,0),则点C的坐标为 .
三.解答题
25.在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,﹣2),B(2,﹣1),C(4,﹣3).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)以点O为位似中心,在网格中画出△A1B1C1的位似图形△A2B2C2,使△A2B2C2与△A1B1C1的相似比为2:1;
(3)设点P(a,b)为△ABC内一点,则依上述两次变换后点P在△A2B2C2内的对应点P2的坐标是 .
26.如图,利用直尺、计算机或图形计算器任意画一个△ABC,以点O为位似中心,自选相似比k,进行位似变换,得到△A'B′C′.度量线段OA,OA′,OB,OB′,OC,OC′的长,你有什么发现?任意改变△ABC的位置,得出的结论是否仍然成立?
27.已知,△ABC在平面直角坐标系的位置如图所示,点A,B,C的坐标分别为(1,0),(4,﹣1),(3,2).△A1B1C1与△ABC是以点P为位似中心的位似图形.
(1)请画出点P的位置,并写出点P的坐标 ;
(2)以点O为位似中心,在y轴左侧画出△ABC的位似图形△A2B2C2,使相似比为1:1,若点M(a,b)为△ABC内一点,则点M在△A2B2C2内的对应点的坐标为 .
28.如图,已知O是坐标原点,AB两点的坐标分别为(3,﹣1),(2,1).
(1)以点O为位似中心,在y轴的左侧将△OAB放大2倍;
(2)分别写出A,B两点的对应点A',B'的坐标.
29.如图,△ABC与△DOE是位似图形,A(0,3),B(﹣2,0),C(1,0),E(6,0),△ABC与△DOE的位似中心为M.
(1)写出D点的坐标;
(2)在图中画出M点,并求M点的坐标.
30.如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(3,0),C(1,﹣1),AC交x轴于点P.
(1)∠ACB的度数为 ;
(2)P点坐标为 ;
(3)以点O为位似中心,将△ABC放大为原来的2倍,请在图中画出所有符合条件的三角形.
答案
一.选择题
C.D.C.B.B.A.D.C.D.C.D.C.
二.填空题
13.(2.5,0).
14.(6,3)或(﹣6,﹣3).
15.(12,6)或(﹣12,﹣6).
16.(2.5,3).
17.(,).
18.(,2).
19.(4,3)或(﹣4,﹣3).
20.(2,1)或(﹣2,﹣1).
21.1:3.
22.(0,2).
23.12.
24.(1,1).
三.解答题
25.解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作;
(3)点P的对应点P2的坐标是(2a,﹣2b).
故答案为(2a,﹣2b).
26.解:经测量,OA=2cm,OA′=1cm,OB=3cm,OB′=1.5cm,OC=3cm,OC′=1.5cm,
可以得到,2,
∴A′B′∥AB,A′C′∥AC,C′B′∥CB,即位似图形的对应边互相平行,
任意改变△ABC的位置,得到△A'B′C′,△ABC与△A'B′C′的对应边互相平行,
即意改变△ABC的位置,得出的结论仍然成立.
27.解:(1)如图所示:点P(0,﹣2);
(2)如图所示:△A2B2C2即为所求,点M对应点的坐标为:(﹣a,﹣b).
故答案为:(1)(0,﹣2);(2)(﹣a,﹣b).
28.解:(1)如图所示:△OA′B′,即为所求;
(2)A'的坐标是(﹣6,2),B'的坐标是(﹣4,﹣2).
29.解:(1)过点D作DH⊥OE于点H,
∵△ABC与△DOE是位似图形,A(0,3),B(﹣2,0),C(1,0),E(6,0),
∴BC=3,OE=6,△AOB∽△DHO,
∴位似比为:3:6=1:2,
∴OH=2OB=4,DH=2OA=6,
∴D点的坐标为:(4,6);
(2)连接DA并延长,交x轴于点M,则点M即为△ABC与△DOE的位似中心;
则MO:MH=1:2,
设MO=x,则MH=x+4,
∴x:(x+4)=1:2,
解得:x=4,
∴M点的坐标为(﹣4,0 ).
30.解:(1)∵∠ABC=90°,AB=CB,
∴△ABC为等腰直角三角形,
∴∠ACB=45°;
故答案为:45°;
(2)由题意得:A(2,2),C(1,﹣1),
设直线AC解析式为y=kx+b,
把A与C坐标代入得:,
解得:,即直线AC解析式为y=3x﹣4,
令y=0,得到x,
则P的坐标为(,0);
故答案为:(,0);
(3)如图所示:△A1B1C1和△A2B2C2为所求三角形.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
