九年级数学下册试题 7.1正切-苏科版(含答案)
文档属性
| 名称 | 九年级数学下册试题 7.1正切-苏科版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 185.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 12:58:52 | ||
图片预览



文档简介
7.1正切
一.选择题
1.在Rt△ABC中,∠C=90°,AC=1,AB=3,则下列结论正确的是( )
A.sin B B.cos B C.tan B D.cot B
2.如图,在6×6的正方形网格中,△ABC的顶点都在小正方形的顶点上,则tan∠BAC的值是( )
A. B. C. D.
3.在Rt△ABC中,∠C=90°,则下列正确的等式可以是( )
A.2sinA﹣3=0 B.cos2B=1 C.tan B+1=0 D.tan2 A=3
4.如图,在2×3的正方形网格中,tan∠ACB的值为( )
A. B. C. D.2
5.已知Rt△ABC中,∠C=90°,b为∠B的对边,a为∠A的对边,若b与∠A已知,则下列各式正确的是( )
A.a=bsin∠A B.a=bcos∠A C.a=btan∠A D.a=b÷tan∠A
6.如图,四边形ABCD的顶点都在正方形网格的格点上,则tan∠CBD的值为( )
A. B.1 C. D.
7.将一副直角三角板中的两块按如图摆放,连接AC,则tan∠DAC的值为( )
A. B. C. D.
8.已知⊙O的半径为5,AB是弦,P是直线AB上的一点,PB=3,AB=8,则tan∠OPA的值为( )
A.3 B. C.或 D.3或
9.如图,已知⊙O的半径为5cm,弦AB的长为8cm,P是AB延长线上一点,BP=2cm,则tan∠OPA等于( )
A. B. C.2 D.
10.直角三角形纸片的两直角边长分别为6,8,现将△ABC如图那样折叠,使点A与点B重合,折痕为DE,则tan∠CBE的值是( )
A. B. C. D.
11.如图,延长RT△ABC斜边AB到点D,使BD=AB,连接CD,若tan∠BCD,则tanA=( )
A. B.1 C. D.
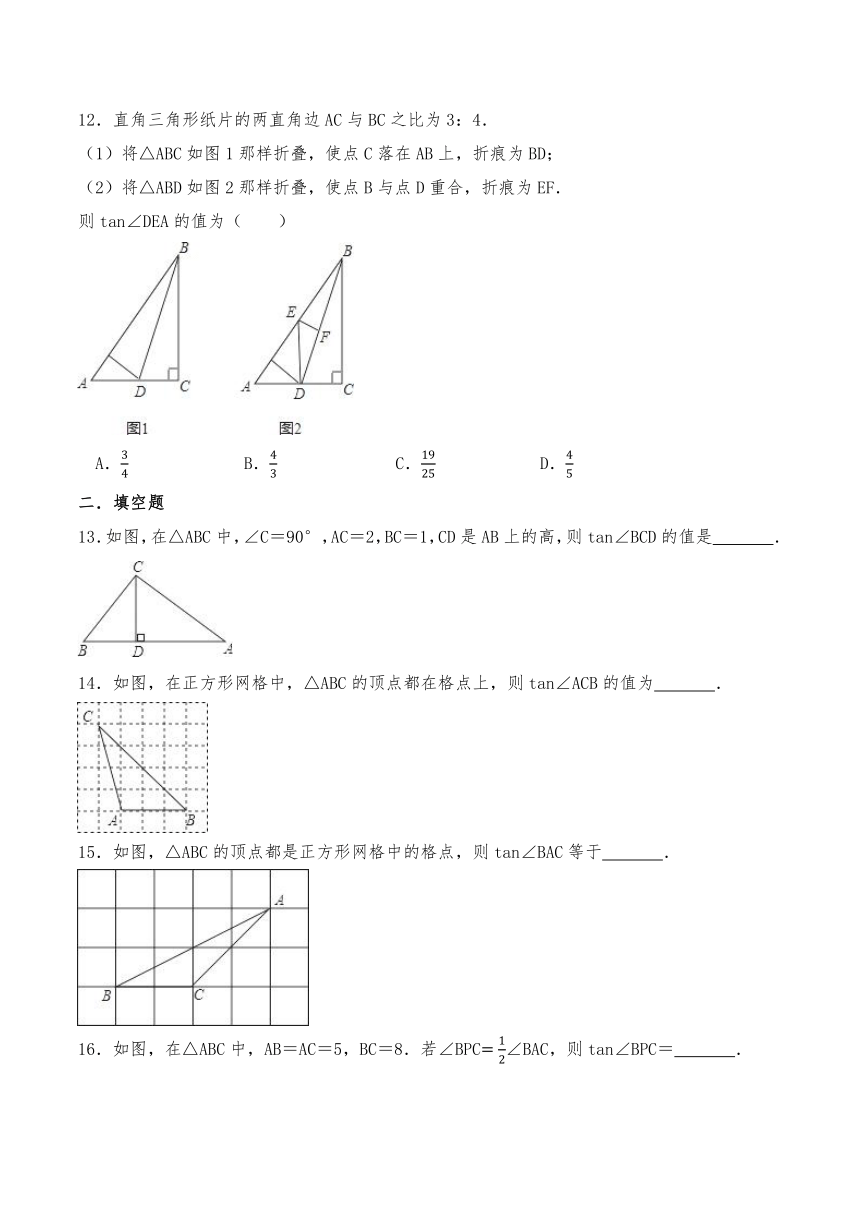
12.直角三角形纸片的两直角边AC与BC之比为3:4.
(1)将△ABC如图1那样折叠,使点C落在AB上,折痕为BD;
(2)将△ABD如图2那样折叠,使点B与点D重合,折痕为EF.
则tan∠DEA的值为( )
A. B. C. D.
二.填空题
13.如图,在△ABC中,∠C=90°,AC=2,BC=1,CD是AB上的高,则tan∠BCD的值是 .
14.如图,在正方形网格中,△ABC的顶点都在格点上,则tan∠ACB的值为 .
15.如图,△ABC的顶点都是正方形网格中的格点,则tan∠BAC等于 .
16.如图,在△ABC中,AB=AC=5,BC=8.若∠BPC∠BAC,则tan∠BPC= .
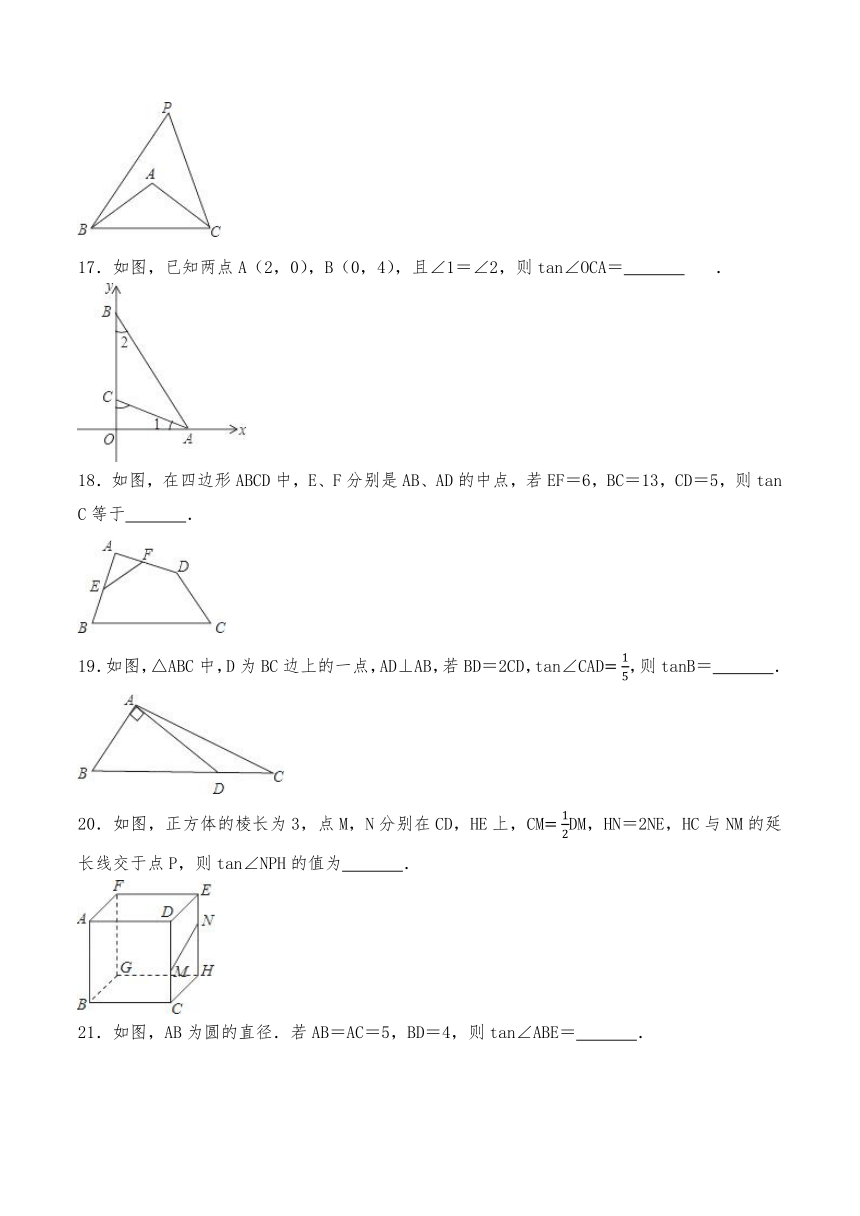
17.如图,已知两点A(2,0),B(0,4),且∠1=∠2,则tan∠OCA= .
18.如图,在四边形ABCD中,E、F分别是AB、AD的中点,若EF=6,BC=13,CD=5,则tan C等于 .
19.如图,△ABC中,D为BC边上的一点,AD⊥AB,若BD=2CD,tan∠CAD,则tanB= .
20.如图,正方体的棱长为3,点M,N分别在CD,HE上,CMDM,HN=2NE,HC与NM的延长线交于点P,则tan∠NPH的值为 .
21.如图,AB为圆的直径.若AB=AC=5,BD=4,则tan∠ABE= .
22.如图,在△ABC中,AB=AC,BD、CE分别为两腰上的中线,且BD⊥CE,则tan∠ABC= .
23.如图,点A在反比例函数y(x>0)的图象上,点B在反比例函数y(x<0)的图象上,且OA⊥OB.线段AB交反比例函数y(x>0)的图象于另一点C,连接OC,若点C为AB的中点,则tan∠OCA的值为 .
24.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足是D,,那么tan∠B的值为 .
三.解答题
25.如图,在Rt△ABC中,∠C=90°,AB=10,tan∠A,求BC的长和sin∠B的值.
26.如图,在平面直角坐标系中,已知点B(4,2),BA⊥x轴于A.
(1)求tan∠BOA的值;
(2)将点B绕原点逆时针方向旋转90°后记作点C,求点C的坐标;
(3)将△OAB平移得到△O′A′B′,点A的对应点是A′,点B的对应点B'的坐标为(2,﹣2),在坐标系中作出△O′A′B′,并写出点O′、A′的坐标.
27.已知:如图,在由边长为1的小正方形组成的网格中,点A、B、C、D、E都在小正方形的顶点上,求tan∠ADC的值.
28.已知:如图,在△ABC中,∠A=90°,AB=6,AC=8,点P从点A开始沿AC边向点C匀速移动,点Q从点A开始沿AB边向点B,再沿BC边向点C匀速移动.若P、Q两点同时从点A出发,则可同时到达点C.
(1)如果P、Q两点同时从点A出发,以原速度按各自的移动路线移动到某一时刻同时停止移动,当点Q移动到BC边上(Q不与C重合)时,求作以tan∠QCA、tan∠QPA为根的一元二次方程;
(2)如果P、Q两点同时从点A出发,以原速度按各自的移动路线移动到某一时刻同时停止移动,当S△PBQ时,求PA的长.
29.矩形ABCD中AB=10,BC=8,E为AD边上一点,沿CE将△CDE对折,使点D正好落在AB边上,求tan∠AFE.
30.如图所示,△ABC内接于⊙O,AB是⊙O的直径,点D在⊙O上,过点C的切线交AD的延长线于点E,且AE⊥CE,连接CD.
(1)求证:DC=BC;
(2)若AB=5,AC=4,求tan∠DCE的值.
答案
一.选择题
C.C.D.D.C.A.C.D.D.C.A.A.
二.填空题
13.;
14..
15..
16..
17.2.
18..
19..
20..
21..
22.3.
23..
24.
三.解答题
25.解:∵tan∠A,
∴AC=2BC,
在Rt△ABC中,AC2+BC2=AB2,
即(2BC)2+BC2=102,
解得BC=2,
∴AC=2BC=4,
sin∠B.
26.解:(1)∵点B(4,2),BA⊥x轴于A,
∴OA=4,BA=2,
∴tan∠BOA.
(2)如图,由旋转可知:CD=BA=2,OD=OA=4,
∴点C的坐标是(﹣2,4).
(3)△O′A′B′如图所示,O′(﹣2,﹣4),A′(2,﹣4).
27.解:根据题意可得,AC=BC,CD=CE,AD=BE=5,
∴△ACD≌△BCE.
∴∠ADC=∠BEC.
∴tan∠ADC=tan∠BEC.
28.解:在Rt△ABC中,AB=6,AC=8,
∴BC=10.
∵P、Q两点从点A同时出发,可同时到达点C,
∴
(1)设P点移动的路程为x,Q点移动的路程为2x.
∴CP=8﹣x,BQ=2x﹣6,CQ=16﹣2x.
作QH⊥AC,垂足为H(如右下图).
∵∠A=90°,∴QH∥AB,
∴
∴,
∴PH=CH﹣CP(8﹣x),
∴tan∠QPA2.
∵tan∠QCA,
∴tan∠QPA+tan∠QCA,
tan∠QPA tan∠QCA,
∴以tan∠QCA、tan∠QPA为根的一元二次方程为
y2即4y2﹣11y+6=0.
(2)当S△PBQ时,设PA=x,点Q的位置有两种情况:
①当点Q在AB上时(如图),
则AQ=2x,BQ=6﹣2x.
S△PBQ
,
∴,
∵△=9,
∴此方程无实根,故点Q不能在AB上;
②当点Q在BC边上时(如图),
则QB=2x﹣6.
作PG⊥BC,垂足为G,
∴△PCG∽△BCA,
∴,
∴,
∴S△PBQ
.
∴x2﹣11x+28=0,
解得:x1=4,x2=7.
∴S△PBQ时,PA=4或7.
29.解:根据图形有:∠AFE+∠EFC+∠BFC=180°,
根据折叠的性质,∠EFC=∠EDC=90°,
即∠AFE+∠BFC=90°,
而Rt△BCF中,有∠BCF+∠BFC=90°,
易得∠AFE=∠BCF,
在Rt△BFC,
根据折叠的性质,有CF=CD,
在Rt△BFC中,BC=8,CF=CD=10,
由勾股定理易得:BF=6,
则tan∠BCF;
故有tan∠AFE=tan∠BCF;
答:tan∠AFE.
30.(1)证明:连接OC.
∵OA=OC,
∴∠OAC=∠OCA.
∵CE是⊙O的切线,
∴∠OCE=90°.
∵AE⊥CE,
∴∠AEC=∠OCE=90°.
∴OC∥AE.
∴∠OCA=∠CAD.
∴∠CAD=∠BAC.
∴.
∴DC=BC.
(2)解:∵AB是⊙O的直径,
∴∠ACB=90°.
∴BC3.
∵∠CAE=∠BAC,∠AEC=∠ACB=90°,
∴△ACE∽△ABC.
∴.
∴,.
∵DC=BC=3,
∴.
∴tan∠DCE.
一.选择题
1.在Rt△ABC中,∠C=90°,AC=1,AB=3,则下列结论正确的是( )
A.sin B B.cos B C.tan B D.cot B
2.如图,在6×6的正方形网格中,△ABC的顶点都在小正方形的顶点上,则tan∠BAC的值是( )
A. B. C. D.
3.在Rt△ABC中,∠C=90°,则下列正确的等式可以是( )
A.2sinA﹣3=0 B.cos2B=1 C.tan B+1=0 D.tan2 A=3
4.如图,在2×3的正方形网格中,tan∠ACB的值为( )
A. B. C. D.2
5.已知Rt△ABC中,∠C=90°,b为∠B的对边,a为∠A的对边,若b与∠A已知,则下列各式正确的是( )
A.a=bsin∠A B.a=bcos∠A C.a=btan∠A D.a=b÷tan∠A
6.如图,四边形ABCD的顶点都在正方形网格的格点上,则tan∠CBD的值为( )
A. B.1 C. D.
7.将一副直角三角板中的两块按如图摆放,连接AC,则tan∠DAC的值为( )
A. B. C. D.
8.已知⊙O的半径为5,AB是弦,P是直线AB上的一点,PB=3,AB=8,则tan∠OPA的值为( )
A.3 B. C.或 D.3或
9.如图,已知⊙O的半径为5cm,弦AB的长为8cm,P是AB延长线上一点,BP=2cm,则tan∠OPA等于( )
A. B. C.2 D.
10.直角三角形纸片的两直角边长分别为6,8,现将△ABC如图那样折叠,使点A与点B重合,折痕为DE,则tan∠CBE的值是( )
A. B. C. D.
11.如图,延长RT△ABC斜边AB到点D,使BD=AB,连接CD,若tan∠BCD,则tanA=( )
A. B.1 C. D.
12.直角三角形纸片的两直角边AC与BC之比为3:4.
(1)将△ABC如图1那样折叠,使点C落在AB上,折痕为BD;
(2)将△ABD如图2那样折叠,使点B与点D重合,折痕为EF.
则tan∠DEA的值为( )
A. B. C. D.
二.填空题
13.如图,在△ABC中,∠C=90°,AC=2,BC=1,CD是AB上的高,则tan∠BCD的值是 .
14.如图,在正方形网格中,△ABC的顶点都在格点上,则tan∠ACB的值为 .
15.如图,△ABC的顶点都是正方形网格中的格点,则tan∠BAC等于 .
16.如图,在△ABC中,AB=AC=5,BC=8.若∠BPC∠BAC,则tan∠BPC= .
17.如图,已知两点A(2,0),B(0,4),且∠1=∠2,则tan∠OCA= .
18.如图,在四边形ABCD中,E、F分别是AB、AD的中点,若EF=6,BC=13,CD=5,则tan C等于 .
19.如图,△ABC中,D为BC边上的一点,AD⊥AB,若BD=2CD,tan∠CAD,则tanB= .
20.如图,正方体的棱长为3,点M,N分别在CD,HE上,CMDM,HN=2NE,HC与NM的延长线交于点P,则tan∠NPH的值为 .
21.如图,AB为圆的直径.若AB=AC=5,BD=4,则tan∠ABE= .
22.如图,在△ABC中,AB=AC,BD、CE分别为两腰上的中线,且BD⊥CE,则tan∠ABC= .
23.如图,点A在反比例函数y(x>0)的图象上,点B在反比例函数y(x<0)的图象上,且OA⊥OB.线段AB交反比例函数y(x>0)的图象于另一点C,连接OC,若点C为AB的中点,则tan∠OCA的值为 .
24.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足是D,,那么tan∠B的值为 .
三.解答题
25.如图,在Rt△ABC中,∠C=90°,AB=10,tan∠A,求BC的长和sin∠B的值.
26.如图,在平面直角坐标系中,已知点B(4,2),BA⊥x轴于A.
(1)求tan∠BOA的值;
(2)将点B绕原点逆时针方向旋转90°后记作点C,求点C的坐标;
(3)将△OAB平移得到△O′A′B′,点A的对应点是A′,点B的对应点B'的坐标为(2,﹣2),在坐标系中作出△O′A′B′,并写出点O′、A′的坐标.
27.已知:如图,在由边长为1的小正方形组成的网格中,点A、B、C、D、E都在小正方形的顶点上,求tan∠ADC的值.
28.已知:如图,在△ABC中,∠A=90°,AB=6,AC=8,点P从点A开始沿AC边向点C匀速移动,点Q从点A开始沿AB边向点B,再沿BC边向点C匀速移动.若P、Q两点同时从点A出发,则可同时到达点C.
(1)如果P、Q两点同时从点A出发,以原速度按各自的移动路线移动到某一时刻同时停止移动,当点Q移动到BC边上(Q不与C重合)时,求作以tan∠QCA、tan∠QPA为根的一元二次方程;
(2)如果P、Q两点同时从点A出发,以原速度按各自的移动路线移动到某一时刻同时停止移动,当S△PBQ时,求PA的长.
29.矩形ABCD中AB=10,BC=8,E为AD边上一点,沿CE将△CDE对折,使点D正好落在AB边上,求tan∠AFE.
30.如图所示,△ABC内接于⊙O,AB是⊙O的直径,点D在⊙O上,过点C的切线交AD的延长线于点E,且AE⊥CE,连接CD.
(1)求证:DC=BC;
(2)若AB=5,AC=4,求tan∠DCE的值.
答案
一.选择题
C.C.D.D.C.A.C.D.D.C.A.A.
二.填空题
13.;
14..
15..
16..
17.2.
18..
19..
20..
21..
22.3.
23..
24.
三.解答题
25.解:∵tan∠A,
∴AC=2BC,
在Rt△ABC中,AC2+BC2=AB2,
即(2BC)2+BC2=102,
解得BC=2,
∴AC=2BC=4,
sin∠B.
26.解:(1)∵点B(4,2),BA⊥x轴于A,
∴OA=4,BA=2,
∴tan∠BOA.
(2)如图,由旋转可知:CD=BA=2,OD=OA=4,
∴点C的坐标是(﹣2,4).
(3)△O′A′B′如图所示,O′(﹣2,﹣4),A′(2,﹣4).
27.解:根据题意可得,AC=BC,CD=CE,AD=BE=5,
∴△ACD≌△BCE.
∴∠ADC=∠BEC.
∴tan∠ADC=tan∠BEC.
28.解:在Rt△ABC中,AB=6,AC=8,
∴BC=10.
∵P、Q两点从点A同时出发,可同时到达点C,
∴
(1)设P点移动的路程为x,Q点移动的路程为2x.
∴CP=8﹣x,BQ=2x﹣6,CQ=16﹣2x.
作QH⊥AC,垂足为H(如右下图).
∵∠A=90°,∴QH∥AB,
∴
∴,
∴PH=CH﹣CP(8﹣x),
∴tan∠QPA2.
∵tan∠QCA,
∴tan∠QPA+tan∠QCA,
tan∠QPA tan∠QCA,
∴以tan∠QCA、tan∠QPA为根的一元二次方程为
y2即4y2﹣11y+6=0.
(2)当S△PBQ时,设PA=x,点Q的位置有两种情况:
①当点Q在AB上时(如图),
则AQ=2x,BQ=6﹣2x.
S△PBQ
,
∴,
∵△=9,
∴此方程无实根,故点Q不能在AB上;
②当点Q在BC边上时(如图),
则QB=2x﹣6.
作PG⊥BC,垂足为G,
∴△PCG∽△BCA,
∴,
∴,
∴S△PBQ
.
∴x2﹣11x+28=0,
解得:x1=4,x2=7.
∴S△PBQ时,PA=4或7.
29.解:根据图形有:∠AFE+∠EFC+∠BFC=180°,
根据折叠的性质,∠EFC=∠EDC=90°,
即∠AFE+∠BFC=90°,
而Rt△BCF中,有∠BCF+∠BFC=90°,
易得∠AFE=∠BCF,
在Rt△BFC,
根据折叠的性质,有CF=CD,
在Rt△BFC中,BC=8,CF=CD=10,
由勾股定理易得:BF=6,
则tan∠BCF;
故有tan∠AFE=tan∠BCF;
答:tan∠AFE.
30.(1)证明:连接OC.
∵OA=OC,
∴∠OAC=∠OCA.
∵CE是⊙O的切线,
∴∠OCE=90°.
∵AE⊥CE,
∴∠AEC=∠OCE=90°.
∴OC∥AE.
∴∠OCA=∠CAD.
∴∠CAD=∠BAC.
∴.
∴DC=BC.
(2)解:∵AB是⊙O的直径,
∴∠ACB=90°.
∴BC3.
∵∠CAE=∠BAC,∠AEC=∠ACB=90°,
∴△ACE∽△ABC.
∴.
∴,.
∵DC=BC=3,
∴.
∴tan∠DCE.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
