九年级数学下册试题 7.6用锐角三角函数解决问题-苏科版(含答案)
文档属性
| 名称 | 九年级数学下册试题 7.6用锐角三角函数解决问题-苏科版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 390.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 00:00:00 | ||
图片预览


文档简介
7.6用锐角三角函数解决问题
一.选择题
1.如图,滑动调节式遮阳伞的立柱AC垂直于地面AB,P为立柱上的滑动调节点,伞体的截面示意图为△PDE,F为PD的中点,AC=2.8m,PD=2m,CF=1m,∠DPE=15°.根据生活经验,当太阳光线与PE垂直时,遮阳效果最佳,在上午10:00时,太阳光线与地面的夹角为65°,若要遮阳效果最佳AP的长约为( )
(参考数据:sin65°≈0.91,cos65°≈0.42,sin50°≈0.77,cos50°≈0.64)
A.1.2m B.1.3m C.1.5m D.2.0m
2.如图,一个直角梯形的堤坝坡长AB为6米,斜坡AB的坡角为60°,为了改善堤坝的稳固性,准备将其坡角改为45°,则调整后的斜坡AE的长度为( )
A.3米 B.3米 C.(32)米 D.(33)米
3.如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为10m,DE的长为5m,则树AB的高度是( )m.
A.10 B.15 C.15 D.155
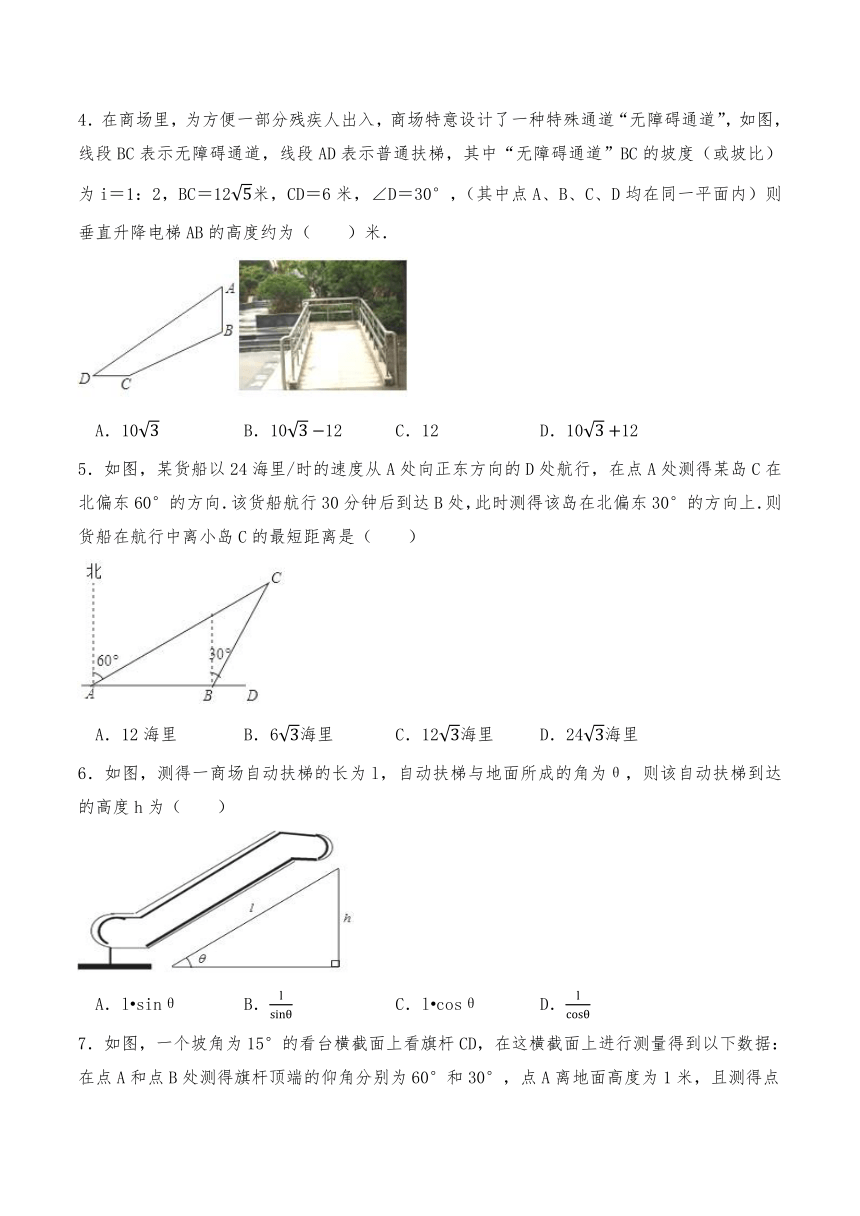
4.在商场里,为方便一部分残疾人出入,商场特意设计了一种特殊通道“无障碍通道”,如图,线段BC表示无障碍通道,线段AD表示普通扶梯,其中“无障碍通道”BC的坡度(或坡比)为i=1:2,BC=12米,CD=6米,∠D=30°,(其中点A、B、C、D均在同一平面内)则垂直升降电梯AB的高度约为( )米.
A.10 B.1012 C.12 D.1012
5.如图,某货船以24海里/时的速度从A处向正东方向的D处航行,在点A处测得某岛C在北偏东60°的方向.该货船航行30分钟后到达B处,此时测得该岛在北偏东30°的方向上.则货船在航行中离小岛C的最短距离是( )
A.12海里 B.6海里 C.12海里 D.24海里
6.如图,测得一商场自动扶梯的长为l,自动扶梯与地面所成的角为θ,则该自动扶梯到达的高度h为( )
A.l sinθ B. C.l cosθ D.
7.如图,一个坡角为15°的看台横截面上看旗杆CD,在这横截面上进行测量得到以下数据:在点A和点B处测得旗杆顶端的仰角分别为60°和30°,点A离地面高度为1米,且测得点A到点B的距离为8米,则旗杆的高度为( )
A.25米 B.24米 C.23米 D.26米
8.如图,电线杆CD的高度为h,两根拉线AC与BC互相垂直(A、D、B在同一条直线上),设∠CAB=α,那么拉线BC的长度为( )
A. B. C. D.
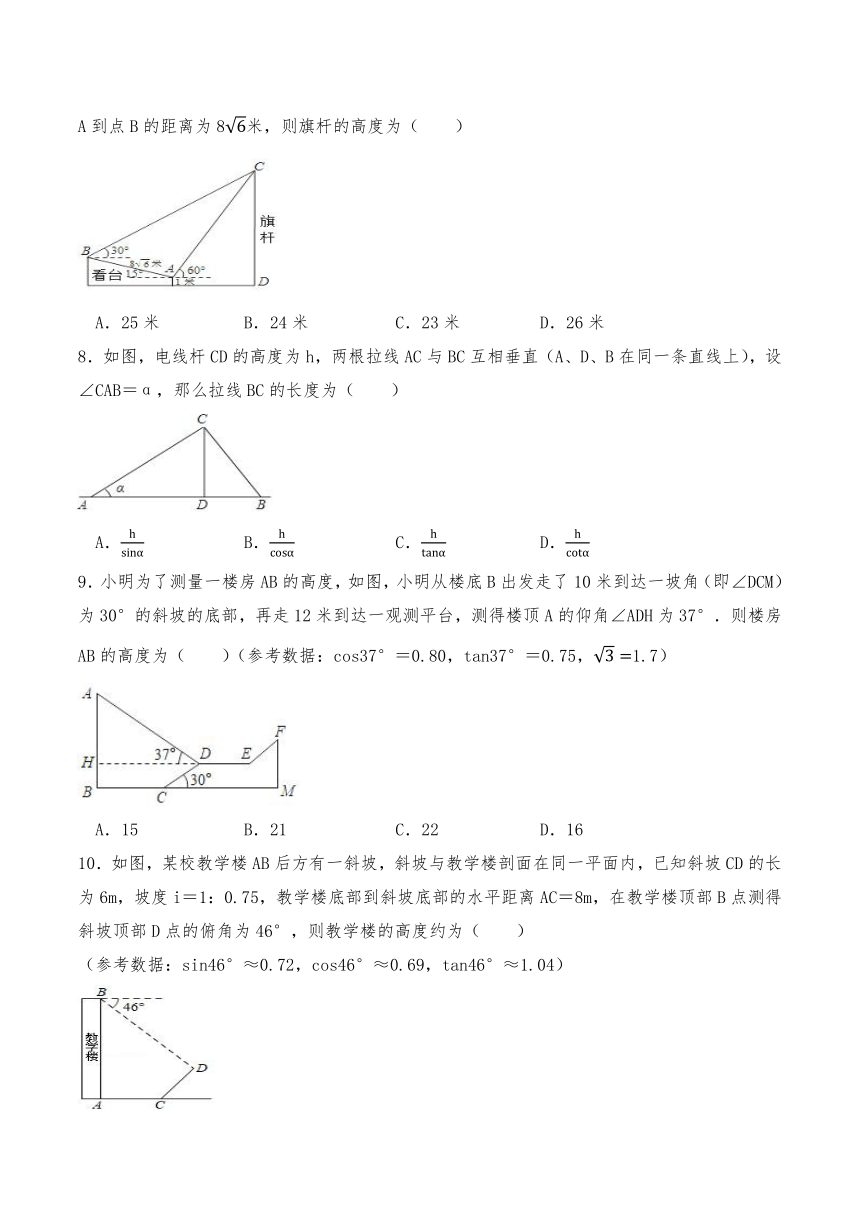
9.小明为了测量一楼房AB的高度,如图,小明从楼底B出发走了10米到达一坡角(即∠DCM)为30°的斜坡的底部,再走12米到达一观测平台,测得楼顶A的仰角∠ADH为37°.则楼房AB的高度为( )(参考数据:cos37°=0.80,tan37°=0.75,1.7)
A.15 B.21 C.22 D.16
10.如图,某校教学楼AB后方有一斜坡,斜坡与教学楼剖面在同一平面内,已知斜坡CD的长为6m,坡度i=1:0.75,教学楼底部到斜坡底部的水平距离AC=8m,在教学楼顶部B点测得斜坡顶部D点的俯角为46°,则教学楼的高度约为( )
(参考数据:sin46°≈0.72,cos46°≈0.69,tan46°≈1.04)
A.12.1m B.13.3m C.16.9m D.18.1m
11.如图,小丽为了测量校园里教学楼AB的高度.将测角仪CD竖直放置在与教学楼水平距离为32m的地面上,若测角仪的高度是1.5m,测得教学楼的顶部A处的仰角为30°,则教学楼的高度约是( )
A.20m B.57m C.18.5m D.17m
12.中国最早的一部数学著作《周髀算经》中记载着勾股定理.约1400年后的汉代数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的证明.这就是如图所示的“赵爽弦图”,若|sina﹣cosa|,则小正方形与直角三角形的面积比为( )
A.1: B.1:1 C.2: D.1:5
二.填空题
13.如图,一轮船在A处观测灯塔P位于南偏西30°方向,该轮船沿正南方向以15海里/时的速度匀速航行2小时后到达B处,再观测灯塔P位于南偏西60°方向.若该轮船继续向南航行至灯塔P最近的位置C处,此时PC长为 海里.
14.如图,码头A在码头B的正东方向,两个码头之间的距离为10海里,今有一货船由码头A出发,沿北偏西60°方向航行到达小岛C处,此时测得码头B在南偏东45°方向,则码头A与小岛C的距离为 海里(结果保留根号).
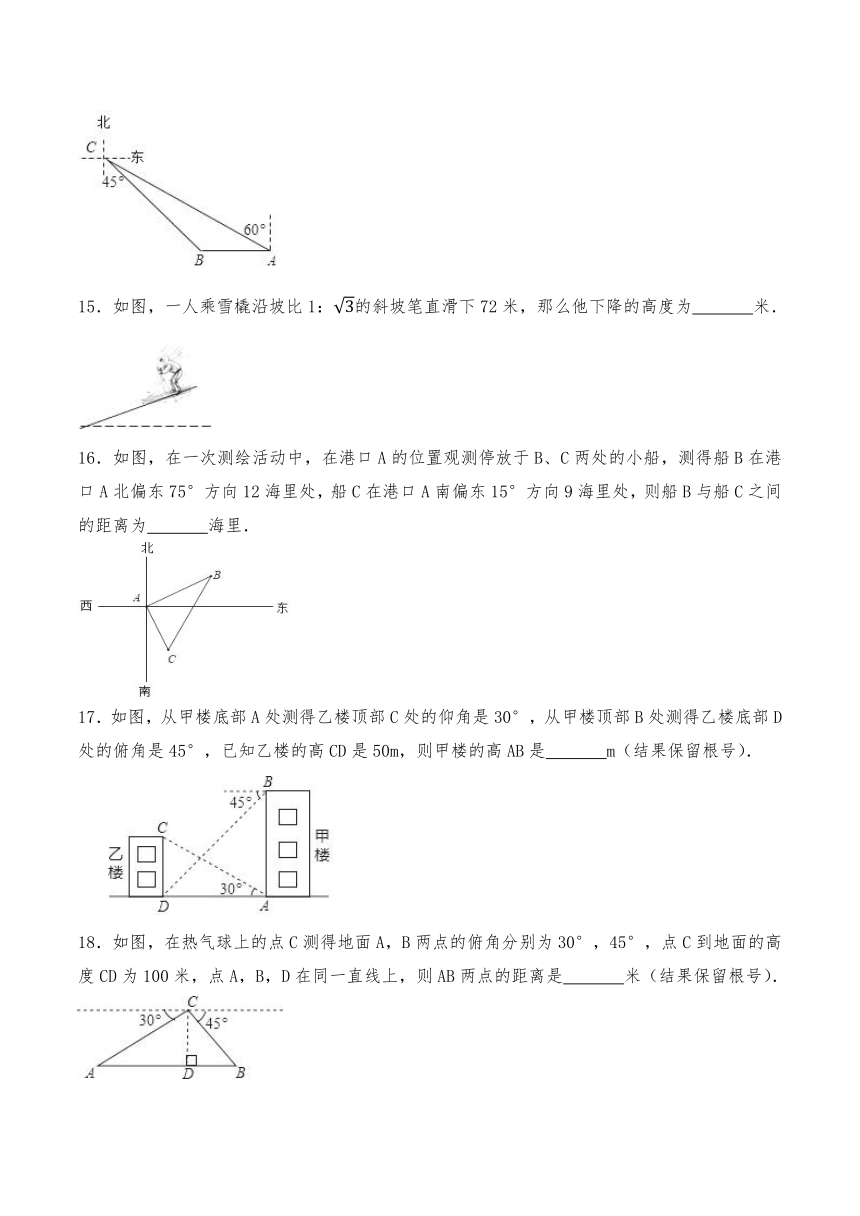
15.如图,一人乘雪橇沿坡比1:的斜坡笔直滑下72米,那么他下降的高度为 米.
16.如图,在一次测绘活动中,在港口A的位置观测停放于B、C两处的小船,测得船B在港口A北偏东75°方向12海里处,船C在港口A南偏东15°方向9海里处,则船B与船C之间的距离为 海里.
17.如图,从甲楼底部A处测得乙楼顶部C处的仰角是30°,从甲楼顶部B处测得乙楼底部D处的俯角是45°,已知乙楼的高CD是50m,则甲楼的高AB是 m(结果保留根号).
18.如图,在热气球上的点C测得地面A,B两点的俯角分别为30°,45°,点C到地面的高度CD为100米,点A,B,D在同一直线上,则AB两点的距离是 米(结果保留根号).
19.如图,一座水库大坝的横断面为梯形ABCD,斜坡AB=8m,现将坡度为1:的斜坡AB改为坡度为1:2的斜坡AP.则新坡面AP= m.(结果保留根号)
20.如图,学校科技小组计划测量一处电信塔的高度,小明在A处用仪器测到塔尖D的仰角∠DAC=15°,向塔正前方水平直行260m到达点B,测到塔尖的仰角∠DBC=30°,若小明的眼睛离地面1.6m,塔的高度DE= m.
21.港珠澳大桥是中国境内一座连接香港、珠海和澳门的桥隧工程,因其超大的建筑规模、空前的施工难度以及顶尖的建造技术而闻名世界.其主体工程青州航道桥是一座双塔双索面钢箱梁斜拉桥,两座索塔及索塔两侧的斜拉索对称分布,塔高AB为163米,大桥主跨BD的中点为E,记斜拉索与大桥主梁所夹锐角为α,那么用塔高和α的三角函数表示主跨BD的长为 米.
22.如图,某建筑物的顶部有一块标识牌CD,小明在斜坡上B处测得标识牌顶部C的仰角为45°,沿斜坡走下来,在地面A处测得标识牌底部D的仰角为60°,已知斜坡AB的坡角为30°,AB=AE=10米.则标识牌CD的高度是 米.
23.图1是一张可以折叠的小床展开后支撑起来放在地面的示意图,此时点A、B、C在同一直线上,且∠ACD=90°,图2是小床支撑脚CD折叠的示意图,在折叠过程中,△ACD变形为四边形ABC'D',最后折叠形成一条线段BD“.某家装厂设计的折叠床是AB=8cm,BC=16cm,
①此时CD应该是多长 ;
②折叠时,当AB⊥BC′时,sinD'= .
24.如图,在坡度为1:2.4的斜坡上有一棵与水平面垂直的树BC,在斜坡底部A处测得树顶C的仰角为30°,AB的长为65米,那么树高BC等于 米(保留根号).
三.解答题
25.速滑运动受到许多年轻人的喜爱.如图,四边形BCDG是某速滑场馆建造的滑台,已知CD∥EG,滑台的高DG为5米,且坡面BC的坡度为1:1.后来为了提高安全性,决定降低坡度,改造后的新坡面AC的坡度为.
(1)求新坡面AC的坡角及AC的长;
(2)原坡面底部BG的正前方10米处(EB=10)是护墙EF,为保证安全,体育管理部门规定,坡面底部至少距护墙7米.请问新的设计方案能否通过,试说明理由(参考数据:)
26.如图,随着社会经济的发展,人们的环境保护意识也在逐步增强.某社区设立了“保护环境爱我地球”的宣传牌.已知立杆AB的高度是3m,从地面上某处D点测得宣传牌顶端C点和底端B点的仰角分别是62°和45°.求宣传牌的高度BC的长.(精确到0.1m,参考数据:sin62°=0.83,cos62°=0.47,tan62°=1.88)
27.如图,在一次综合实践活动中,小亮要测量一楼房的高度,先在坡面D处测得楼房项部A的仰角为30°,沿坡面向下走到坡脚C处,然后向楼房方向继续行走10米到达E处,测得楼房顶部A的仰角为60°,已知坡面CD=10米,山坡的坡度i=1:,(坡度i是指坡面的铅直高度与水平宽度的比),求楼房AB高度(结果精确到1米)(参考数据:1.73,1.41)
28.位于河南省登封市境内的元代观星台,是中国现存最早的天文台,也是世界文化遗产之一.
某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示,他们在地面一条水平步道MP上架设测角仪,先在点M处测得观星台最高点A的仰角为22°,然后沿MP方向前进16m到达点N处,测得点A的仰角为45°.测角仪的高度为1.6m.
(1)求观星台最高点A距离地面的高度(结果精确到0.1m.参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,1.41);
(2)“景点简介”显示,观星台的高度为12.6m.请计算本次测量结果的误差,并提出一条减小误差的合理化建议.
29.2020年5月5日,为我国载人空间站工程研制的长征五号运载火箭在海南文昌首飞成功.运载火箭从地面O处发射,当火箭到达点A时,地面D处的雷达站测得AD=4000米,仰角为30°.3秒后,火箭直线上升到达点B处,此时地面C处的雷达站测得B处的仰角为45°.已知C,D两处相距460米,求火箭从A到B处的平均速度(结果精确到1米/秒,参考数据:1.732,1.414).
30.如图,某学校体育场看台的顶端C到地面的垂直距离CD为2m,看台所在斜坡CM的坡比i=1:3,在点C处测得旗杆顶点A的仰角为30°,在点M处测得旗杆顶点A的仰角为60°,且B,M,D三点在同一水平线上.
(1)求DM的长.
(2)求旗杆AB的高度.(结果保留根号)
答案
一.选择题
C.A.B.B.B.A.A.B.B.C.A.B.
二.填空题
13.15.
14.(10+10).
15.36(米).
16.15.
17.50.
18.100(1)
19.4.
20.131.6.
21.
22.(15﹣5).
23.32;.
24.(2025).
三.解答题
25.解:(1)如图,过点C作CH⊥BG,垂足为H,
∵新坡面AC的坡度为1:,
∴tan∠CAH,
∴∠CAH=30°,即新坡面AC的坡角为30°,
∴AC=2CH=10米;
(2)新的设计方案不能通过.
理由如下:∵坡面BC的坡度为1:1,
∴BH=CH=5,
∵tan∠CAH,
∴AHCH=5,
∴AB=55,
∴AE=EB﹣AB=10﹣(55)=15﹣56.35<7,
∴新的设计方案不能通过.
26.解:在Rt△ADB中,
∵∠BDA=45°,
∴AD=AB=3m.
在Rt△ADC中,AC=AD tan62°=3×1.88=5.64(m).
∴BC=AC﹣AB=5.64﹣3=2.64≈2.6(m).
答:宣传牌BC的高度是2.6m.
27.解:过D作DG⊥BC于G,DH⊥AB于H,交AE于F,作FP⊥BC于P,如图所示:
则DG=FP=BH,DF=GP,
∵坡面CD=10米,山坡的坡度i=1:,
∴∠DCG=30°,
∴FP=DGCD=5,
∴CGDG=5,
∵∠FEP=60°,
∴FPEP=5,
∴EP,
∴DF=GP=51010,
∵∠AEB=60°,
∴∠EAB=30°,
∵∠ADH=30°,
∴∠DAH=60°,
∴∠DAF=30°=∠ADF,
∴AF=DF10,
∴FHAF5,
∴AHFH=10+5,
∴AB=AH+BH=10+55=15+515+5×1.73≈24(米),
答:楼房AB高度约为24米.
28.解:(1)过A作AD⊥PM于D,延长BC交AD于E,
则四边形BMNC,四边形BMDE是矩形,
∴BC=MN=16m,DE=CN=BM=1.6m,
∵∠AEC=90°,∠ACE=45°,
∴△ACE是等腰直角三角形,
∴CE=AE,
设AE=CE=x,
∴BE=16+x,
∵∠ABE=22°,
∴tan22°0.40,
∴x≈10.7(m),
∴AD=10.7+1.6=12.3(m),
答:观星台最高点A距离地面的高度约为12.3m;
(2)∵“景点简介”显示,观星台的高度为12.6m,
∴本次测量结果的误差为12.6﹣12.3=0.3(m),
减小误差的合理化建议为:为了减小误差可以通过多次测量取平均值的方法.
29.解:设火箭从A到B处的平均速度为x米/秒,根据题意可知:
AB=3x,
在Rt△ADO中,∠ADO=30°,AD=4000,
∴AO=2000,
∴DO=2000,
∵CD=460,
∴OC=OD﹣CD=2000460,
在Rt△BOC中,∠BCO=45°,
∴BO=OC,
∵OB=OA+AB=2000+3x,
∴2000+3x=2000460,
解得x≈335(米/秒).
答:火箭从A到B处的平均速度为335米/秒.
30.解:(1)∵CD=2,tan∠CMD,
∴MD=6m;
(2)过点C作CE⊥AB于点E,
设BM=x,
∴BD=x+6,
∵∠AMB=60°,
∴∠BAM=30°,
∴ABx,
已知四边形CDBE是矩形,
∴BE=CD=2,CE=BD=x+6,
∴AE=AB﹣BEx﹣2,
在Rt△ACE中,
∵tan30°,
∴,
解得:x=3,
∴ABx=(33)(m).
一.选择题
1.如图,滑动调节式遮阳伞的立柱AC垂直于地面AB,P为立柱上的滑动调节点,伞体的截面示意图为△PDE,F为PD的中点,AC=2.8m,PD=2m,CF=1m,∠DPE=15°.根据生活经验,当太阳光线与PE垂直时,遮阳效果最佳,在上午10:00时,太阳光线与地面的夹角为65°,若要遮阳效果最佳AP的长约为( )
(参考数据:sin65°≈0.91,cos65°≈0.42,sin50°≈0.77,cos50°≈0.64)
A.1.2m B.1.3m C.1.5m D.2.0m
2.如图,一个直角梯形的堤坝坡长AB为6米,斜坡AB的坡角为60°,为了改善堤坝的稳固性,准备将其坡角改为45°,则调整后的斜坡AE的长度为( )
A.3米 B.3米 C.(32)米 D.(33)米
3.如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为10m,DE的长为5m,则树AB的高度是( )m.
A.10 B.15 C.15 D.155
4.在商场里,为方便一部分残疾人出入,商场特意设计了一种特殊通道“无障碍通道”,如图,线段BC表示无障碍通道,线段AD表示普通扶梯,其中“无障碍通道”BC的坡度(或坡比)为i=1:2,BC=12米,CD=6米,∠D=30°,(其中点A、B、C、D均在同一平面内)则垂直升降电梯AB的高度约为( )米.
A.10 B.1012 C.12 D.1012
5.如图,某货船以24海里/时的速度从A处向正东方向的D处航行,在点A处测得某岛C在北偏东60°的方向.该货船航行30分钟后到达B处,此时测得该岛在北偏东30°的方向上.则货船在航行中离小岛C的最短距离是( )
A.12海里 B.6海里 C.12海里 D.24海里
6.如图,测得一商场自动扶梯的长为l,自动扶梯与地面所成的角为θ,则该自动扶梯到达的高度h为( )
A.l sinθ B. C.l cosθ D.
7.如图,一个坡角为15°的看台横截面上看旗杆CD,在这横截面上进行测量得到以下数据:在点A和点B处测得旗杆顶端的仰角分别为60°和30°,点A离地面高度为1米,且测得点A到点B的距离为8米,则旗杆的高度为( )
A.25米 B.24米 C.23米 D.26米
8.如图,电线杆CD的高度为h,两根拉线AC与BC互相垂直(A、D、B在同一条直线上),设∠CAB=α,那么拉线BC的长度为( )
A. B. C. D.
9.小明为了测量一楼房AB的高度,如图,小明从楼底B出发走了10米到达一坡角(即∠DCM)为30°的斜坡的底部,再走12米到达一观测平台,测得楼顶A的仰角∠ADH为37°.则楼房AB的高度为( )(参考数据:cos37°=0.80,tan37°=0.75,1.7)
A.15 B.21 C.22 D.16
10.如图,某校教学楼AB后方有一斜坡,斜坡与教学楼剖面在同一平面内,已知斜坡CD的长为6m,坡度i=1:0.75,教学楼底部到斜坡底部的水平距离AC=8m,在教学楼顶部B点测得斜坡顶部D点的俯角为46°,则教学楼的高度约为( )
(参考数据:sin46°≈0.72,cos46°≈0.69,tan46°≈1.04)
A.12.1m B.13.3m C.16.9m D.18.1m
11.如图,小丽为了测量校园里教学楼AB的高度.将测角仪CD竖直放置在与教学楼水平距离为32m的地面上,若测角仪的高度是1.5m,测得教学楼的顶部A处的仰角为30°,则教学楼的高度约是( )
A.20m B.57m C.18.5m D.17m
12.中国最早的一部数学著作《周髀算经》中记载着勾股定理.约1400年后的汉代数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的证明.这就是如图所示的“赵爽弦图”,若|sina﹣cosa|,则小正方形与直角三角形的面积比为( )
A.1: B.1:1 C.2: D.1:5
二.填空题
13.如图,一轮船在A处观测灯塔P位于南偏西30°方向,该轮船沿正南方向以15海里/时的速度匀速航行2小时后到达B处,再观测灯塔P位于南偏西60°方向.若该轮船继续向南航行至灯塔P最近的位置C处,此时PC长为 海里.
14.如图,码头A在码头B的正东方向,两个码头之间的距离为10海里,今有一货船由码头A出发,沿北偏西60°方向航行到达小岛C处,此时测得码头B在南偏东45°方向,则码头A与小岛C的距离为 海里(结果保留根号).
15.如图,一人乘雪橇沿坡比1:的斜坡笔直滑下72米,那么他下降的高度为 米.
16.如图,在一次测绘活动中,在港口A的位置观测停放于B、C两处的小船,测得船B在港口A北偏东75°方向12海里处,船C在港口A南偏东15°方向9海里处,则船B与船C之间的距离为 海里.
17.如图,从甲楼底部A处测得乙楼顶部C处的仰角是30°,从甲楼顶部B处测得乙楼底部D处的俯角是45°,已知乙楼的高CD是50m,则甲楼的高AB是 m(结果保留根号).
18.如图,在热气球上的点C测得地面A,B两点的俯角分别为30°,45°,点C到地面的高度CD为100米,点A,B,D在同一直线上,则AB两点的距离是 米(结果保留根号).
19.如图,一座水库大坝的横断面为梯形ABCD,斜坡AB=8m,现将坡度为1:的斜坡AB改为坡度为1:2的斜坡AP.则新坡面AP= m.(结果保留根号)
20.如图,学校科技小组计划测量一处电信塔的高度,小明在A处用仪器测到塔尖D的仰角∠DAC=15°,向塔正前方水平直行260m到达点B,测到塔尖的仰角∠DBC=30°,若小明的眼睛离地面1.6m,塔的高度DE= m.
21.港珠澳大桥是中国境内一座连接香港、珠海和澳门的桥隧工程,因其超大的建筑规模、空前的施工难度以及顶尖的建造技术而闻名世界.其主体工程青州航道桥是一座双塔双索面钢箱梁斜拉桥,两座索塔及索塔两侧的斜拉索对称分布,塔高AB为163米,大桥主跨BD的中点为E,记斜拉索与大桥主梁所夹锐角为α,那么用塔高和α的三角函数表示主跨BD的长为 米.
22.如图,某建筑物的顶部有一块标识牌CD,小明在斜坡上B处测得标识牌顶部C的仰角为45°,沿斜坡走下来,在地面A处测得标识牌底部D的仰角为60°,已知斜坡AB的坡角为30°,AB=AE=10米.则标识牌CD的高度是 米.
23.图1是一张可以折叠的小床展开后支撑起来放在地面的示意图,此时点A、B、C在同一直线上,且∠ACD=90°,图2是小床支撑脚CD折叠的示意图,在折叠过程中,△ACD变形为四边形ABC'D',最后折叠形成一条线段BD“.某家装厂设计的折叠床是AB=8cm,BC=16cm,
①此时CD应该是多长 ;
②折叠时,当AB⊥BC′时,sinD'= .
24.如图,在坡度为1:2.4的斜坡上有一棵与水平面垂直的树BC,在斜坡底部A处测得树顶C的仰角为30°,AB的长为65米,那么树高BC等于 米(保留根号).
三.解答题
25.速滑运动受到许多年轻人的喜爱.如图,四边形BCDG是某速滑场馆建造的滑台,已知CD∥EG,滑台的高DG为5米,且坡面BC的坡度为1:1.后来为了提高安全性,决定降低坡度,改造后的新坡面AC的坡度为.
(1)求新坡面AC的坡角及AC的长;
(2)原坡面底部BG的正前方10米处(EB=10)是护墙EF,为保证安全,体育管理部门规定,坡面底部至少距护墙7米.请问新的设计方案能否通过,试说明理由(参考数据:)
26.如图,随着社会经济的发展,人们的环境保护意识也在逐步增强.某社区设立了“保护环境爱我地球”的宣传牌.已知立杆AB的高度是3m,从地面上某处D点测得宣传牌顶端C点和底端B点的仰角分别是62°和45°.求宣传牌的高度BC的长.(精确到0.1m,参考数据:sin62°=0.83,cos62°=0.47,tan62°=1.88)
27.如图,在一次综合实践活动中,小亮要测量一楼房的高度,先在坡面D处测得楼房项部A的仰角为30°,沿坡面向下走到坡脚C处,然后向楼房方向继续行走10米到达E处,测得楼房顶部A的仰角为60°,已知坡面CD=10米,山坡的坡度i=1:,(坡度i是指坡面的铅直高度与水平宽度的比),求楼房AB高度(结果精确到1米)(参考数据:1.73,1.41)
28.位于河南省登封市境内的元代观星台,是中国现存最早的天文台,也是世界文化遗产之一.
某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示,他们在地面一条水平步道MP上架设测角仪,先在点M处测得观星台最高点A的仰角为22°,然后沿MP方向前进16m到达点N处,测得点A的仰角为45°.测角仪的高度为1.6m.
(1)求观星台最高点A距离地面的高度(结果精确到0.1m.参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,1.41);
(2)“景点简介”显示,观星台的高度为12.6m.请计算本次测量结果的误差,并提出一条减小误差的合理化建议.
29.2020年5月5日,为我国载人空间站工程研制的长征五号运载火箭在海南文昌首飞成功.运载火箭从地面O处发射,当火箭到达点A时,地面D处的雷达站测得AD=4000米,仰角为30°.3秒后,火箭直线上升到达点B处,此时地面C处的雷达站测得B处的仰角为45°.已知C,D两处相距460米,求火箭从A到B处的平均速度(结果精确到1米/秒,参考数据:1.732,1.414).
30.如图,某学校体育场看台的顶端C到地面的垂直距离CD为2m,看台所在斜坡CM的坡比i=1:3,在点C处测得旗杆顶点A的仰角为30°,在点M处测得旗杆顶点A的仰角为60°,且B,M,D三点在同一水平线上.
(1)求DM的长.
(2)求旗杆AB的高度.(结果保留根号)
答案
一.选择题
C.A.B.B.B.A.A.B.B.C.A.B.
二.填空题
13.15.
14.(10+10).
15.36(米).
16.15.
17.50.
18.100(1)
19.4.
20.131.6.
21.
22.(15﹣5).
23.32;.
24.(2025).
三.解答题
25.解:(1)如图,过点C作CH⊥BG,垂足为H,
∵新坡面AC的坡度为1:,
∴tan∠CAH,
∴∠CAH=30°,即新坡面AC的坡角为30°,
∴AC=2CH=10米;
(2)新的设计方案不能通过.
理由如下:∵坡面BC的坡度为1:1,
∴BH=CH=5,
∵tan∠CAH,
∴AHCH=5,
∴AB=55,
∴AE=EB﹣AB=10﹣(55)=15﹣56.35<7,
∴新的设计方案不能通过.
26.解:在Rt△ADB中,
∵∠BDA=45°,
∴AD=AB=3m.
在Rt△ADC中,AC=AD tan62°=3×1.88=5.64(m).
∴BC=AC﹣AB=5.64﹣3=2.64≈2.6(m).
答:宣传牌BC的高度是2.6m.
27.解:过D作DG⊥BC于G,DH⊥AB于H,交AE于F,作FP⊥BC于P,如图所示:
则DG=FP=BH,DF=GP,
∵坡面CD=10米,山坡的坡度i=1:,
∴∠DCG=30°,
∴FP=DGCD=5,
∴CGDG=5,
∵∠FEP=60°,
∴FPEP=5,
∴EP,
∴DF=GP=51010,
∵∠AEB=60°,
∴∠EAB=30°,
∵∠ADH=30°,
∴∠DAH=60°,
∴∠DAF=30°=∠ADF,
∴AF=DF10,
∴FHAF5,
∴AHFH=10+5,
∴AB=AH+BH=10+55=15+515+5×1.73≈24(米),
答:楼房AB高度约为24米.
28.解:(1)过A作AD⊥PM于D,延长BC交AD于E,
则四边形BMNC,四边形BMDE是矩形,
∴BC=MN=16m,DE=CN=BM=1.6m,
∵∠AEC=90°,∠ACE=45°,
∴△ACE是等腰直角三角形,
∴CE=AE,
设AE=CE=x,
∴BE=16+x,
∵∠ABE=22°,
∴tan22°0.40,
∴x≈10.7(m),
∴AD=10.7+1.6=12.3(m),
答:观星台最高点A距离地面的高度约为12.3m;
(2)∵“景点简介”显示,观星台的高度为12.6m,
∴本次测量结果的误差为12.6﹣12.3=0.3(m),
减小误差的合理化建议为:为了减小误差可以通过多次测量取平均值的方法.
29.解:设火箭从A到B处的平均速度为x米/秒,根据题意可知:
AB=3x,
在Rt△ADO中,∠ADO=30°,AD=4000,
∴AO=2000,
∴DO=2000,
∵CD=460,
∴OC=OD﹣CD=2000460,
在Rt△BOC中,∠BCO=45°,
∴BO=OC,
∵OB=OA+AB=2000+3x,
∴2000+3x=2000460,
解得x≈335(米/秒).
答:火箭从A到B处的平均速度为335米/秒.
30.解:(1)∵CD=2,tan∠CMD,
∴MD=6m;
(2)过点C作CE⊥AB于点E,
设BM=x,
∴BD=x+6,
∵∠AMB=60°,
∴∠BAM=30°,
∴ABx,
已知四边形CDBE是矩形,
∴BE=CD=2,CE=BD=x+6,
∴AE=AB﹣BEx﹣2,
在Rt△ACE中,
∵tan30°,
∴,
解得:x=3,
∴ABx=(33)(m).
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
