苏科版九年级数学下册第七章锐角三角函数单元复习试题 (含答案)
文档属性
| 名称 | 苏科版九年级数学下册第七章锐角三角函数单元复习试题 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 254.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 13:43:54 | ||
图片预览


文档简介
第七章《锐角三角函数》单元复习
一.选择题
1. 如图,传送带和地面所成斜坡的坡度为1:3,若它把物体从地面店A处送到离地面1米高的B处,则物体从A到B所经过的路程为( )
A.3米 B.米 C.2米 D.3米
2. 如图,直线OA过点(2,1),直线OA与x轴的夹角为α,则tanα的值为( )
A. B. C.2 D.
3. 如图,在地面上的点A处测得树顶B的仰角为α,AC=2,则树高BC为( )(用含α的代数式表示)
A.2sinα B.2tanα C.2cosα D.
4. 如图,在某居民楼AB楼顶有一广告牌BC,在距楼底A点左侧水平距离30m的D点处有一个山坡,山坡DE的坡度(或坡比)i=1:2.4,山坡坡底D点到坡顶E点的距离DE=26m,在坡底D点处测得居民楼楼顶B点的仰角为45°,在坡顶E点处测得居民楼楼顶广告牌上端C点的仰角为27°,居民楼AB,广告牌BC与山坡DE的剖面在同一平面内,则广告牌BC的高度约为( )(结果精确到0.1,参考数据:sin27°≈0.45,cos27°≈0.89,tan27°≈0.51)
A.4.5m B.4.8m C.7.1m D.7.5m
5. 如图,从渔船A处测得灯塔M在北偏东55°方向上,这艘渔船以28km/h的速度向正东方向航行,半小时后到达B处,在B处测得灯塔M在北偏东20°方向上,此时灯塔M与渔船的距离是( )
A.28km B.14km C.7km D.14km
6. 数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A,B的距离,他们设计了如图的测量方案:从树A沿着垂直于AB的方向走到E,再从E沿着垂直于AE的方向走到F,C为AE上一点,其中4位同学分别测得四组数据:①AC,∠ACB;②EF,DE,AD;③CD,∠ACB,∠ADB;④∠F,∠ADB,FB.其中能根据所测数据求得A,B两树距离的有( )
A.1组 B.2组 C.3组 D.4组
7. 数学兴趣小组的同学们要测量某大桥主架顶端离水面的高CD.在桥外一点A测得大桥主架与水面的交汇点C的俯角为α,大桥主架的顶端D的仰角为45°,测得与大桥主架的水平距离AB为100米.则大桥主架顶端离水面的高CD为( )
A.(100+100 sinα )米 B.(100+100 tanα )米
C.(100)米 D.(100)米
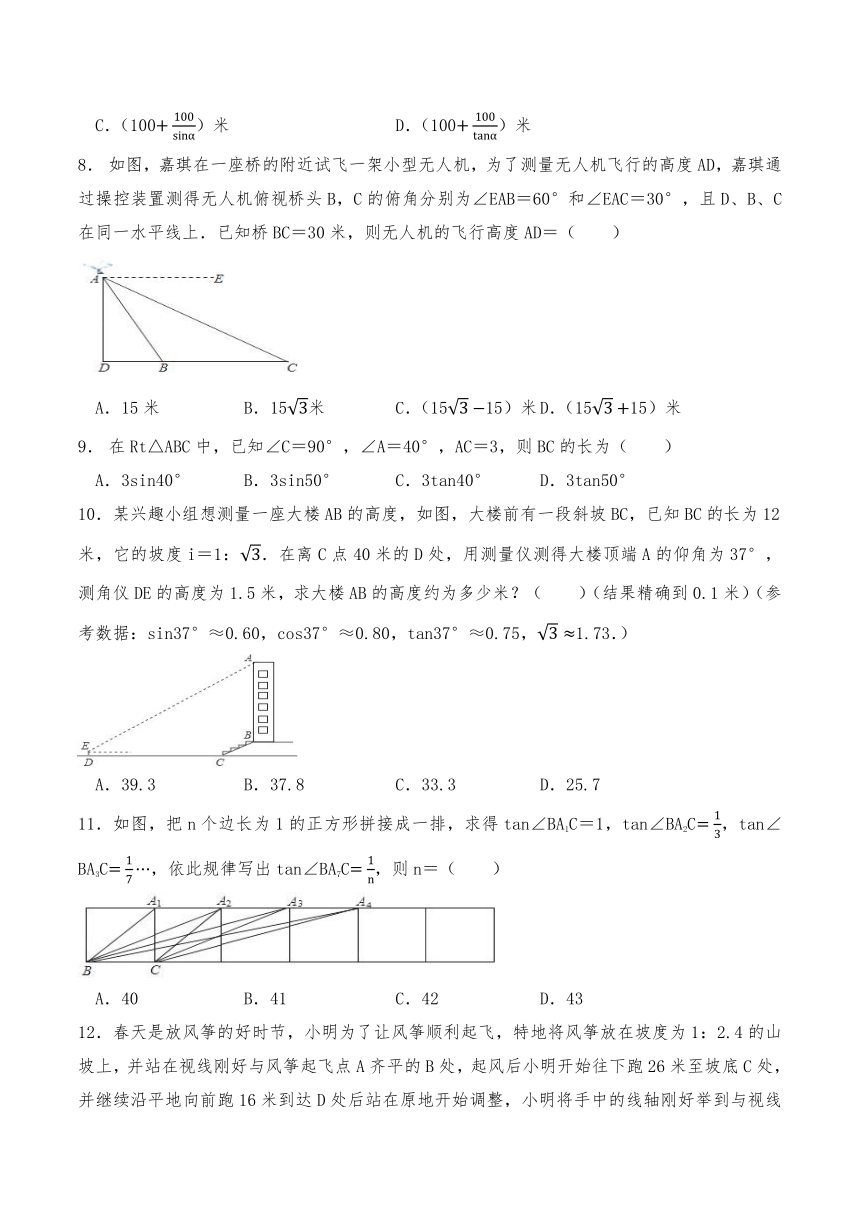
8. 如图,嘉琪在一座桥的附近试飞一架小型无人机,为了测量无人机飞行的高度AD,嘉琪通过操控装置测得无人机俯视桥头B,C的俯角分别为∠EAB=60°和∠EAC=30°,且D、B、C在同一水平线上.已知桥BC=30米,则无人机的飞行高度AD=( )
A.15米 B.15米 C.(1515)米 D.(1515)米
9. 在Rt△ABC中,已知∠C=90°,∠A=40°,AC=3,则BC的长为( )
A.3sin40° B.3sin50° C.3tan40° D.3tan50°
10.某兴趣小组想测量一座大楼AB的高度,如图,大楼前有一段斜坡BC,已知BC的长为12米,它的坡度i=1:.在离C点40米的D处,用测量仪测得大楼顶端A的仰角为37°,测角仪DE的高度为1.5米,求大楼AB的高度约为多少米?( )(结果精确到0.1米)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,1.73.)
A.39.3 B.37.8 C.33.3 D.25.7
11.如图,把n个边长为1的正方形拼接成一排,求得tan∠BA1C=1,tan∠BA2C,tan∠BA3C,依此规律写出tan∠BA7C,则n=( )
A.40 B.41 C.42 D.43
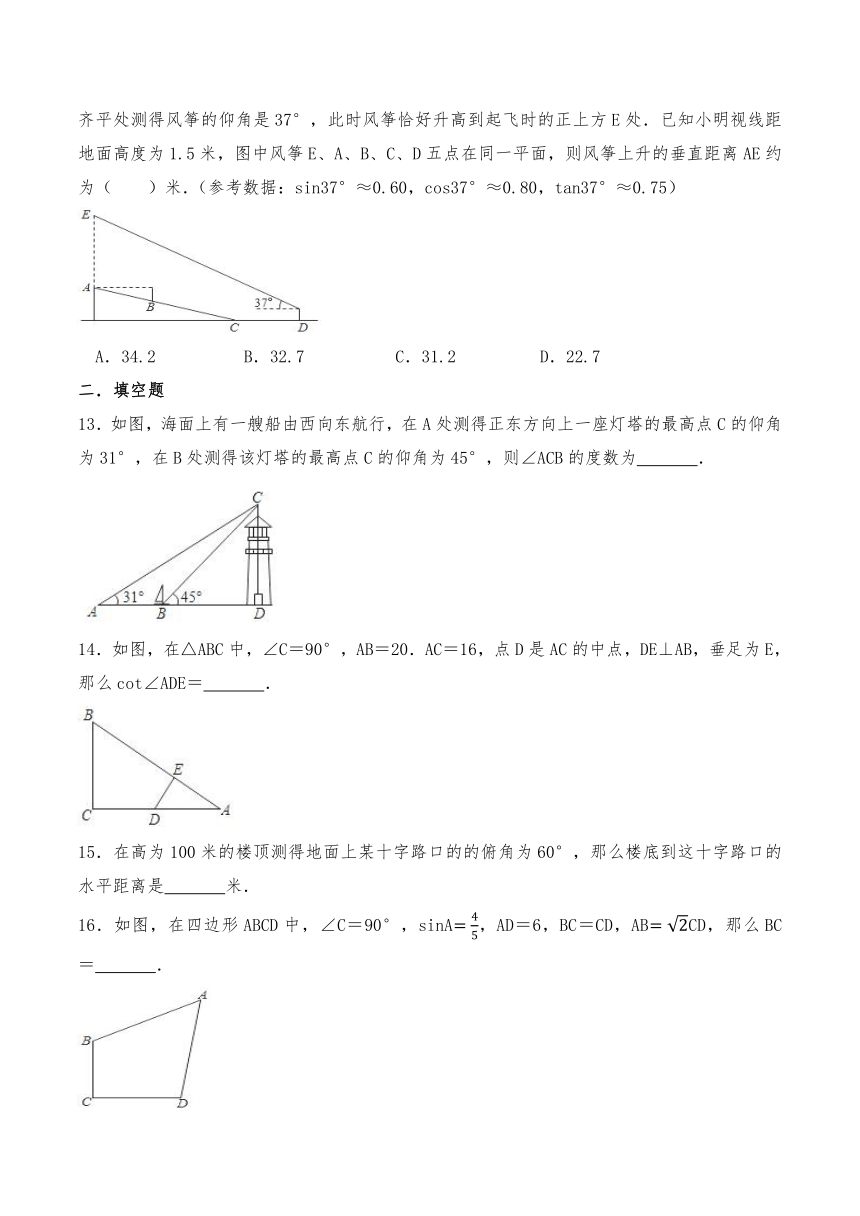
12.春天是放风筝的好时节,小明为了让风筝顺利起飞,特地将风筝放在坡度为1:2.4的山坡上,并站在视线刚好与风筝起飞点A齐平的B处,起风后小明开始往下跑26米至坡底C处,并继续沿平地向前跑16米到达D处后站在原地开始调整,小明将手中的线轴刚好举到与视线齐平处测得风筝的仰角是37°,此时风筝恰好升高到起飞时的正上方E处.已知小明视线距地面高度为1.5米,图中风筝E、A、B、C、D五点在同一平面,则风筝上升的垂直距离AE约为( )米.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
A.34.2 B.32.7 C.31.2 D.22.7
二.填空题
13.如图,海面上有一艘船由西向东航行,在A处测得正东方向上一座灯塔的最高点C的仰角为31°,在B处测得该灯塔的最高点C的仰角为45°,则∠ACB的度数为 .
14.如图,在△ABC中,∠C=90°,AB=20.AC=16,点D是AC的中点,DE⊥AB,垂足为E,那么cot∠ADE= .
15.在高为100米的楼顶测得地面上某十字路口的的俯角为60°,那么楼底到这十字路口的水平距离是 米.
16.如图,在四边形ABCD中,∠C=90°,sinA,AD=6,BC=CD,ABCD,那么BC= .
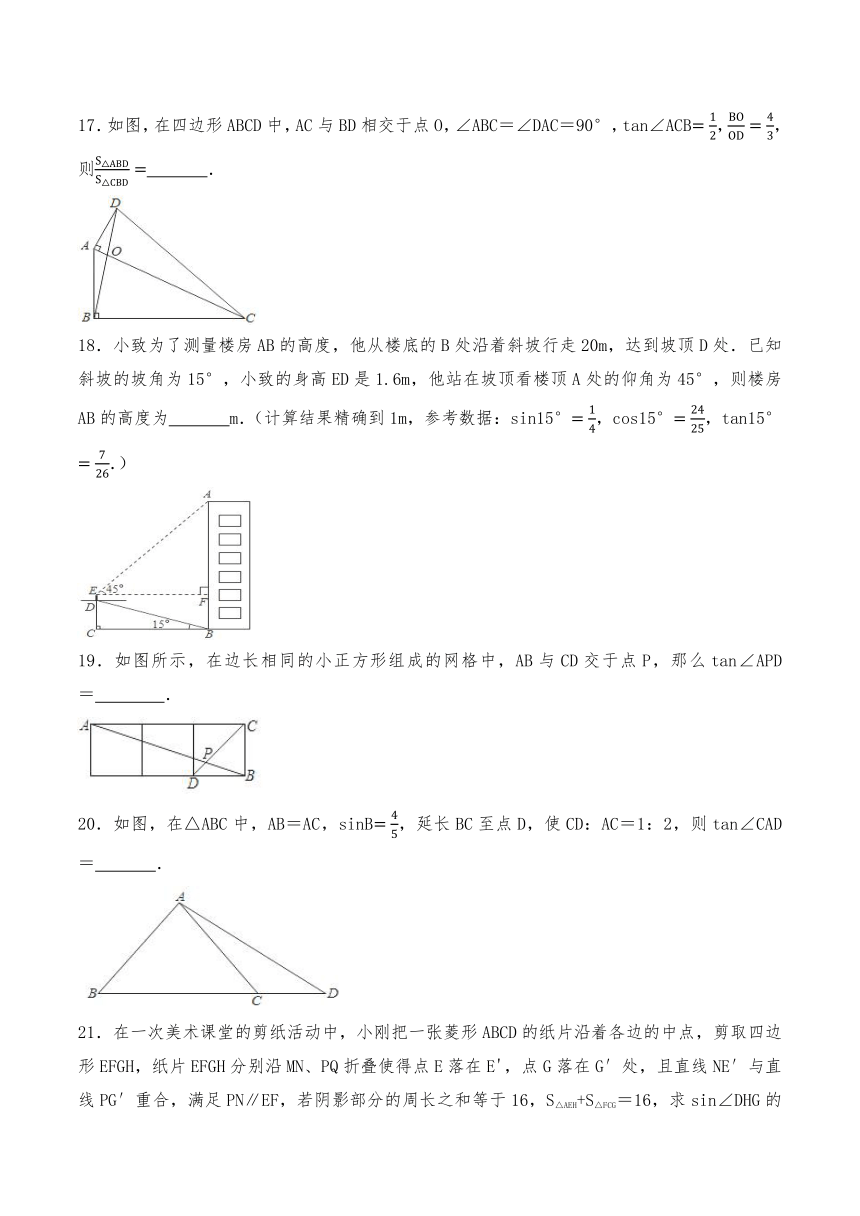
17.如图,在四边形ABCD中,AC与BD相交于点O,∠ABC=∠DAC=90°,tan∠ACB,,则 .
18.小致为了测量楼房AB的高度,他从楼底的B处沿着斜坡行走20m,达到坡顶D处.已知斜坡的坡角为15°,小致的身高ED是1.6m,他站在坡顶看楼顶A处的仰角为45°,则楼房AB的高度为 m.(计算结果精确到1m,参考数据:sin15°,cos15°,tan15°.)
19.如图所示,在边长相同的小正方形组成的网格中,AB与CD交于点P,那么tan∠APD= .
20.如图,在△ABC中,AB=AC,sinB,延长BC至点D,使CD:AC=1:2,则tan∠CAD= .
21.在一次美术课堂的剪纸活动中,小刚把一张菱形ABCD的纸片沿着各边的中点,剪取四边形EFGH,纸片EFGH分别沿MN、PQ折叠使得点E落在E',点G落在G′处,且直线NE′与直线PG′重合,满足PN∥EF,若阴影部分的周长之和等于16,S△AEH+S△FCG=16,求sin∠DHG的值是 .
22.如图,CD是Rt△ABC斜边上的高线,若sinA,BD=1,则AD= .
23.如图,sin∠O,长度为2的线段DE在射线OB上滑动,点C在射线OA上,且OC=5,△CDE的两个内角的角平分线相交于点F,过点F作FG⊥DE,垂足为G,则FG的最大值为 .
24.如图,在△ABC中,AB=AC,BC=12,D为AC边的中点,线段BD的垂直平分线分别与边BC,AB交于点E,F,连接DF,EF.设BE=x,tan∠ACB=y.给出以下结论:①DF∥BC;②△BDE的面积为;③△CDE的周长为12+x;④x2﹣y2=9;⑤2x﹣y2=9.其中正确结论有 (把你认为正确结论的序号都填上).
三.解答题
25.某中学依山而建,校门A处有一坡度i=5:12的斜坡AB,长度为26米,在坡顶B处看教学楼CF的楼顶C的仰角∠CBF=45°,离B点4米远的E处有一个花台,在E处仰望C的仰角∠CEF=60°,CF的延长线交校门处的水平面于点D,求DC的长(结果保留根号).
26.如图,在距某居民楼AB楼底B点左侧水平距离60m的C点处有一个山坡,山坡CD的坡度(或坡比)i=1:0.75,山坡坡底C点到坡顶D点的距离CD=50m,在坡顶D点处测得居民楼楼顶A点的仰角为28°,居民楼AB与山坡CD的剖面在同一平面内,求居民楼AB的高度.(参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)
27.智能手机如果安装了一款测量软件“SmartMeasure”后,就可以测量物高、宽度和面积等,如图,打开软件后将手机摄像头对准脚部按键,再对准头部按键,即可测量出人体的高度.测量者AB用其数学原理如图②所示,测量一棵大树CD,手机显示AC=20m,AD=25m,∠CAD=53°,求此时CD的高.(结果保留根号)(sin53°,cos53°,tan53°)
28.今年第16号台风“浪卡”已经于10月13日在海南琼海市登录.台风来袭时,某绿化带一棵笔直且垂直于地面的大树AB被刮倾斜后在C处折断倒在地上,树的顶部恰好接触到地面D处,测得∠ACD=60°,∠ADC=37°,AD=5米,求这棵大树AB的高.(结果精确到0.1米)(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,1.73)
29.如图,某湖心岛上有一亭子A,在亭子A的正东方向上的湖边有一棵树B,在这个湖心岛的湖边C处测得亭子A在北偏西45°方向上,测得树B在北偏东36°方向上,又测得B、C之间的距离等于200米,求A、B之间的距离
(结果精确到1米).(参考数据:1.414,sin36°≈0.588,cos36°≈0.809,tan36°≈0.727,cot36°≈1.376)
30.某校九年级数学兴趣小组的活动课题是“测量物体高度”.小组成员小明与小红分别采用不同的方案测量同一个底面为圆形的古塔高度,以下是他们研究报告的部分记录内容:
课题:测量古塔的高度
小明的研究报告 小红的研究报告
图示
测量方案与测量数据 用距离地面高度为1.6m的测角器测出古塔顶端的仰角为35°,再用皮尺测得测角器所在位置与古塔底部边缘的最短距离为30m. 在点A用距离地面高度为1.6m的测角器测出古塔顶端的仰角为17°,然后沿AD方向走58.8m到达点B,测出古塔顶端的仰角为45°.
参考数据 sin35°≈0.57,cos35°≈0.82,tan35°≈0.70 sin17°≈0.29,cos17°≈0.96,tan17°≈0.30,1.41
计算古塔高度 (结果精确到0.1m) 30×tan35°+1.6≈22.6(m)
(1)写出小红研究报告中“计算古塔高度”的解答过程;
(2)数学老师说小红的结果较准确,而小明的结果与古塔的实际高度偏差较大.针对小明的测量方案分析测量发生偏差的原因;
(3)利用小明与小红的测量数据,估算该古塔底面圆直径的长度为 m.
答案
一.选择题
B.B.B.D.B.C.B.B.C.C.D.D.
二.填空题
13.14°.
14..
15..
16..
17..
18.26.
19.2.
20..
21..
22.2.
23..
24.②⑤.
三.解答题
25.过点B作BM⊥AD于M,如图所示:
∵i=5:12,
∴,
∵AB=26米,
∴BM=10米,AM=24米,
∴DF=BM=10米,
设EF为x米,则BF=(4+x)米,
∵∠CBF=45°,
∴BF=CF=(4+x)米,
∵∠CEF=60°,
∴tan60°,
即,
解得:x=22,
∴CF=(6+2)米,
∴CD=CF+DF=6+210=16+2(米),
答:DC的长度为(16+2)米.
26.如图,过点D作DF⊥AB,垂足为F,作DE⊥BC交BC的延长线于点E,
由题意得,∠ADF=28°,CD=50m,BC=60m,
在Rt△DEC中,
∵山坡CD的坡度i=1:0.75,
∴,
设DE=4x,则EC=3x,由勾股定理可得CD=5x,
又CD=50,即5x=50,
∴x=10,
∴EC=3x=30(m),DE=4x=40(m)=FB,
∴BE=BC+EC=60+30=90(m)=DF,
在Rt△ADF中,
AF=tan28°×DF≈0.53×90≈47.7(m),
∴AB=AF+FB=47.7+40≈87.7(m),
即居民楼AB的高度约为87.7m.
27.如图②中,过点D作DH⊥AC于H,
在Rt△ADH中,cos∠CAD,sin∠CAD,
∴AH=AD cos53°≈2515(m),DH=AD sin53°≈2520(m),
∵AC=20m,
∴CH=AC﹣AH=5(m),
∴CD5(m).
28.过点A作AE⊥CD于点E,则∠AEC=∠AED=90°.
在Rt△AED中,∠ADC=37°,
∴cos37°,
∴DE≈4,
∵sin37°0.6,
∴AE≈3,
在Rt△AEC中,
∵∠CAE=90°﹣∠ACE=90°﹣60°=30°,
∴CEAE,
∴AC=2CE=2,
∴AB=AC+CE+ED=24=34≈9.2(米).
答:这棵大树AB原来的高度约是9.2米.
29.过点C作CH⊥AB,垂足为点H,
由题意,得∠ACH=45°,∠BCH=36°,BC=200,
在Rt△BHC中,,
∴,
∵sin36°≈0.588,
∴BH≈117.6,
又,
∴.
∵cos36°≈0.809,
∴HC≈161.8,
在Rt△AHC中,,
∵∠ACH=45°,
∴AH=HC,
∴AH≈161.8,
又AB=AH+BH,
∴AB≈279.4,
∴AB≈279(米),
答:A、B之间的距离为279米.
30.(1)设CH=x,
在Rt△CHF中,∵∠CFH=∠FCH=45°,
∴CH=FH=x,
在Rt△CHE中,
∵tan∠CEH,
∴tan17°=0.30,
∴x=25.2,即CH=25.2(m),
∴CD=CH+DH=25.2+1.6=26.8(m),
答:古塔CD的高度为26.8m;
(2)原因:小明测量的只是测角器所在位置与古塔底部边缘的最短距离,不是测量测角器所在位置与底面圆心的最短距离.
(3)如图,
在EH上取一点P使∠CPH=35°,则PG=30,在Rt△CHP中,CH=25.2,∴PH36,
∴GH=PH﹣PG=6,
∴该古塔底面圆直径的长度=2×6=12(m).
故答案为12.
一.选择题
1. 如图,传送带和地面所成斜坡的坡度为1:3,若它把物体从地面店A处送到离地面1米高的B处,则物体从A到B所经过的路程为( )
A.3米 B.米 C.2米 D.3米
2. 如图,直线OA过点(2,1),直线OA与x轴的夹角为α,则tanα的值为( )
A. B. C.2 D.
3. 如图,在地面上的点A处测得树顶B的仰角为α,AC=2,则树高BC为( )(用含α的代数式表示)
A.2sinα B.2tanα C.2cosα D.
4. 如图,在某居民楼AB楼顶有一广告牌BC,在距楼底A点左侧水平距离30m的D点处有一个山坡,山坡DE的坡度(或坡比)i=1:2.4,山坡坡底D点到坡顶E点的距离DE=26m,在坡底D点处测得居民楼楼顶B点的仰角为45°,在坡顶E点处测得居民楼楼顶广告牌上端C点的仰角为27°,居民楼AB,广告牌BC与山坡DE的剖面在同一平面内,则广告牌BC的高度约为( )(结果精确到0.1,参考数据:sin27°≈0.45,cos27°≈0.89,tan27°≈0.51)
A.4.5m B.4.8m C.7.1m D.7.5m
5. 如图,从渔船A处测得灯塔M在北偏东55°方向上,这艘渔船以28km/h的速度向正东方向航行,半小时后到达B处,在B处测得灯塔M在北偏东20°方向上,此时灯塔M与渔船的距离是( )
A.28km B.14km C.7km D.14km
6. 数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A,B的距离,他们设计了如图的测量方案:从树A沿着垂直于AB的方向走到E,再从E沿着垂直于AE的方向走到F,C为AE上一点,其中4位同学分别测得四组数据:①AC,∠ACB;②EF,DE,AD;③CD,∠ACB,∠ADB;④∠F,∠ADB,FB.其中能根据所测数据求得A,B两树距离的有( )
A.1组 B.2组 C.3组 D.4组
7. 数学兴趣小组的同学们要测量某大桥主架顶端离水面的高CD.在桥外一点A测得大桥主架与水面的交汇点C的俯角为α,大桥主架的顶端D的仰角为45°,测得与大桥主架的水平距离AB为100米.则大桥主架顶端离水面的高CD为( )
A.(100+100 sinα )米 B.(100+100 tanα )米
C.(100)米 D.(100)米
8. 如图,嘉琪在一座桥的附近试飞一架小型无人机,为了测量无人机飞行的高度AD,嘉琪通过操控装置测得无人机俯视桥头B,C的俯角分别为∠EAB=60°和∠EAC=30°,且D、B、C在同一水平线上.已知桥BC=30米,则无人机的飞行高度AD=( )
A.15米 B.15米 C.(1515)米 D.(1515)米
9. 在Rt△ABC中,已知∠C=90°,∠A=40°,AC=3,则BC的长为( )
A.3sin40° B.3sin50° C.3tan40° D.3tan50°
10.某兴趣小组想测量一座大楼AB的高度,如图,大楼前有一段斜坡BC,已知BC的长为12米,它的坡度i=1:.在离C点40米的D处,用测量仪测得大楼顶端A的仰角为37°,测角仪DE的高度为1.5米,求大楼AB的高度约为多少米?( )(结果精确到0.1米)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,1.73.)
A.39.3 B.37.8 C.33.3 D.25.7
11.如图,把n个边长为1的正方形拼接成一排,求得tan∠BA1C=1,tan∠BA2C,tan∠BA3C,依此规律写出tan∠BA7C,则n=( )
A.40 B.41 C.42 D.43
12.春天是放风筝的好时节,小明为了让风筝顺利起飞,特地将风筝放在坡度为1:2.4的山坡上,并站在视线刚好与风筝起飞点A齐平的B处,起风后小明开始往下跑26米至坡底C处,并继续沿平地向前跑16米到达D处后站在原地开始调整,小明将手中的线轴刚好举到与视线齐平处测得风筝的仰角是37°,此时风筝恰好升高到起飞时的正上方E处.已知小明视线距地面高度为1.5米,图中风筝E、A、B、C、D五点在同一平面,则风筝上升的垂直距离AE约为( )米.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
A.34.2 B.32.7 C.31.2 D.22.7
二.填空题
13.如图,海面上有一艘船由西向东航行,在A处测得正东方向上一座灯塔的最高点C的仰角为31°,在B处测得该灯塔的最高点C的仰角为45°,则∠ACB的度数为 .
14.如图,在△ABC中,∠C=90°,AB=20.AC=16,点D是AC的中点,DE⊥AB,垂足为E,那么cot∠ADE= .
15.在高为100米的楼顶测得地面上某十字路口的的俯角为60°,那么楼底到这十字路口的水平距离是 米.
16.如图,在四边形ABCD中,∠C=90°,sinA,AD=6,BC=CD,ABCD,那么BC= .
17.如图,在四边形ABCD中,AC与BD相交于点O,∠ABC=∠DAC=90°,tan∠ACB,,则 .
18.小致为了测量楼房AB的高度,他从楼底的B处沿着斜坡行走20m,达到坡顶D处.已知斜坡的坡角为15°,小致的身高ED是1.6m,他站在坡顶看楼顶A处的仰角为45°,则楼房AB的高度为 m.(计算结果精确到1m,参考数据:sin15°,cos15°,tan15°.)
19.如图所示,在边长相同的小正方形组成的网格中,AB与CD交于点P,那么tan∠APD= .
20.如图,在△ABC中,AB=AC,sinB,延长BC至点D,使CD:AC=1:2,则tan∠CAD= .
21.在一次美术课堂的剪纸活动中,小刚把一张菱形ABCD的纸片沿着各边的中点,剪取四边形EFGH,纸片EFGH分别沿MN、PQ折叠使得点E落在E',点G落在G′处,且直线NE′与直线PG′重合,满足PN∥EF,若阴影部分的周长之和等于16,S△AEH+S△FCG=16,求sin∠DHG的值是 .
22.如图,CD是Rt△ABC斜边上的高线,若sinA,BD=1,则AD= .
23.如图,sin∠O,长度为2的线段DE在射线OB上滑动,点C在射线OA上,且OC=5,△CDE的两个内角的角平分线相交于点F,过点F作FG⊥DE,垂足为G,则FG的最大值为 .
24.如图,在△ABC中,AB=AC,BC=12,D为AC边的中点,线段BD的垂直平分线分别与边BC,AB交于点E,F,连接DF,EF.设BE=x,tan∠ACB=y.给出以下结论:①DF∥BC;②△BDE的面积为;③△CDE的周长为12+x;④x2﹣y2=9;⑤2x﹣y2=9.其中正确结论有 (把你认为正确结论的序号都填上).
三.解答题
25.某中学依山而建,校门A处有一坡度i=5:12的斜坡AB,长度为26米,在坡顶B处看教学楼CF的楼顶C的仰角∠CBF=45°,离B点4米远的E处有一个花台,在E处仰望C的仰角∠CEF=60°,CF的延长线交校门处的水平面于点D,求DC的长(结果保留根号).
26.如图,在距某居民楼AB楼底B点左侧水平距离60m的C点处有一个山坡,山坡CD的坡度(或坡比)i=1:0.75,山坡坡底C点到坡顶D点的距离CD=50m,在坡顶D点处测得居民楼楼顶A点的仰角为28°,居民楼AB与山坡CD的剖面在同一平面内,求居民楼AB的高度.(参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)
27.智能手机如果安装了一款测量软件“SmartMeasure”后,就可以测量物高、宽度和面积等,如图,打开软件后将手机摄像头对准脚部按键,再对准头部按键,即可测量出人体的高度.测量者AB用其数学原理如图②所示,测量一棵大树CD,手机显示AC=20m,AD=25m,∠CAD=53°,求此时CD的高.(结果保留根号)(sin53°,cos53°,tan53°)
28.今年第16号台风“浪卡”已经于10月13日在海南琼海市登录.台风来袭时,某绿化带一棵笔直且垂直于地面的大树AB被刮倾斜后在C处折断倒在地上,树的顶部恰好接触到地面D处,测得∠ACD=60°,∠ADC=37°,AD=5米,求这棵大树AB的高.(结果精确到0.1米)(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,1.73)
29.如图,某湖心岛上有一亭子A,在亭子A的正东方向上的湖边有一棵树B,在这个湖心岛的湖边C处测得亭子A在北偏西45°方向上,测得树B在北偏东36°方向上,又测得B、C之间的距离等于200米,求A、B之间的距离
(结果精确到1米).(参考数据:1.414,sin36°≈0.588,cos36°≈0.809,tan36°≈0.727,cot36°≈1.376)
30.某校九年级数学兴趣小组的活动课题是“测量物体高度”.小组成员小明与小红分别采用不同的方案测量同一个底面为圆形的古塔高度,以下是他们研究报告的部分记录内容:
课题:测量古塔的高度
小明的研究报告 小红的研究报告
图示
测量方案与测量数据 用距离地面高度为1.6m的测角器测出古塔顶端的仰角为35°,再用皮尺测得测角器所在位置与古塔底部边缘的最短距离为30m. 在点A用距离地面高度为1.6m的测角器测出古塔顶端的仰角为17°,然后沿AD方向走58.8m到达点B,测出古塔顶端的仰角为45°.
参考数据 sin35°≈0.57,cos35°≈0.82,tan35°≈0.70 sin17°≈0.29,cos17°≈0.96,tan17°≈0.30,1.41
计算古塔高度 (结果精确到0.1m) 30×tan35°+1.6≈22.6(m)
(1)写出小红研究报告中“计算古塔高度”的解答过程;
(2)数学老师说小红的结果较准确,而小明的结果与古塔的实际高度偏差较大.针对小明的测量方案分析测量发生偏差的原因;
(3)利用小明与小红的测量数据,估算该古塔底面圆直径的长度为 m.
答案
一.选择题
B.B.B.D.B.C.B.B.C.C.D.D.
二.填空题
13.14°.
14..
15..
16..
17..
18.26.
19.2.
20..
21..
22.2.
23..
24.②⑤.
三.解答题
25.过点B作BM⊥AD于M,如图所示:
∵i=5:12,
∴,
∵AB=26米,
∴BM=10米,AM=24米,
∴DF=BM=10米,
设EF为x米,则BF=(4+x)米,
∵∠CBF=45°,
∴BF=CF=(4+x)米,
∵∠CEF=60°,
∴tan60°,
即,
解得:x=22,
∴CF=(6+2)米,
∴CD=CF+DF=6+210=16+2(米),
答:DC的长度为(16+2)米.
26.如图,过点D作DF⊥AB,垂足为F,作DE⊥BC交BC的延长线于点E,
由题意得,∠ADF=28°,CD=50m,BC=60m,
在Rt△DEC中,
∵山坡CD的坡度i=1:0.75,
∴,
设DE=4x,则EC=3x,由勾股定理可得CD=5x,
又CD=50,即5x=50,
∴x=10,
∴EC=3x=30(m),DE=4x=40(m)=FB,
∴BE=BC+EC=60+30=90(m)=DF,
在Rt△ADF中,
AF=tan28°×DF≈0.53×90≈47.7(m),
∴AB=AF+FB=47.7+40≈87.7(m),
即居民楼AB的高度约为87.7m.
27.如图②中,过点D作DH⊥AC于H,
在Rt△ADH中,cos∠CAD,sin∠CAD,
∴AH=AD cos53°≈2515(m),DH=AD sin53°≈2520(m),
∵AC=20m,
∴CH=AC﹣AH=5(m),
∴CD5(m).
28.过点A作AE⊥CD于点E,则∠AEC=∠AED=90°.
在Rt△AED中,∠ADC=37°,
∴cos37°,
∴DE≈4,
∵sin37°0.6,
∴AE≈3,
在Rt△AEC中,
∵∠CAE=90°﹣∠ACE=90°﹣60°=30°,
∴CEAE,
∴AC=2CE=2,
∴AB=AC+CE+ED=24=34≈9.2(米).
答:这棵大树AB原来的高度约是9.2米.
29.过点C作CH⊥AB,垂足为点H,
由题意,得∠ACH=45°,∠BCH=36°,BC=200,
在Rt△BHC中,,
∴,
∵sin36°≈0.588,
∴BH≈117.6,
又,
∴.
∵cos36°≈0.809,
∴HC≈161.8,
在Rt△AHC中,,
∵∠ACH=45°,
∴AH=HC,
∴AH≈161.8,
又AB=AH+BH,
∴AB≈279.4,
∴AB≈279(米),
答:A、B之间的距离为279米.
30.(1)设CH=x,
在Rt△CHF中,∵∠CFH=∠FCH=45°,
∴CH=FH=x,
在Rt△CHE中,
∵tan∠CEH,
∴tan17°=0.30,
∴x=25.2,即CH=25.2(m),
∴CD=CH+DH=25.2+1.6=26.8(m),
答:古塔CD的高度为26.8m;
(2)原因:小明测量的只是测角器所在位置与古塔底部边缘的最短距离,不是测量测角器所在位置与底面圆心的最短距离.
(3)如图,
在EH上取一点P使∠CPH=35°,则PG=30,在Rt△CHP中,CH=25.2,∴PH36,
∴GH=PH﹣PG=6,
∴该古塔底面圆直径的长度=2×6=12(m).
故答案为12.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
