8.2 角的比较课件(共16张PPT) 青岛版七年级数学下册
文档属性
| 名称 | 8.2 角的比较课件(共16张PPT) 青岛版七年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 761.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 14:28:37 | ||
图片预览



文档简介
(共16张PPT)
8.2 角的比较
1.会用“度量法”和“叠合法”比较角的大小;
2.理解角的和、差、倍、分,会进行角的加、减、倍、分运算;
3.理解平分线的概念,会运用角平分线进行有关的运算.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
复习导入
1. 如图,已知线段AB、CD,你有哪些办法比较它们的长短?
1.目测法
2.度量法
3.叠合法
思考:类比线段大小的比较,你认为该如何比较两个角的大小?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(一)角的大小比较
1、目测法
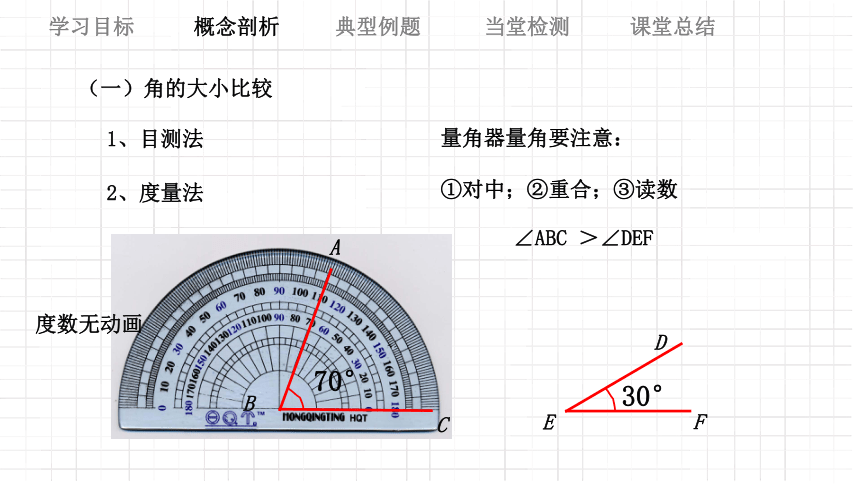
2、度量法
量角器量角要注意:
①对中;②重合;③读数
A
B
70°
C
F
E
D
30°
∠ABC >∠DEF
度数无动画
典型例题
当堂检测
学习目标
课堂总结
概念剖析
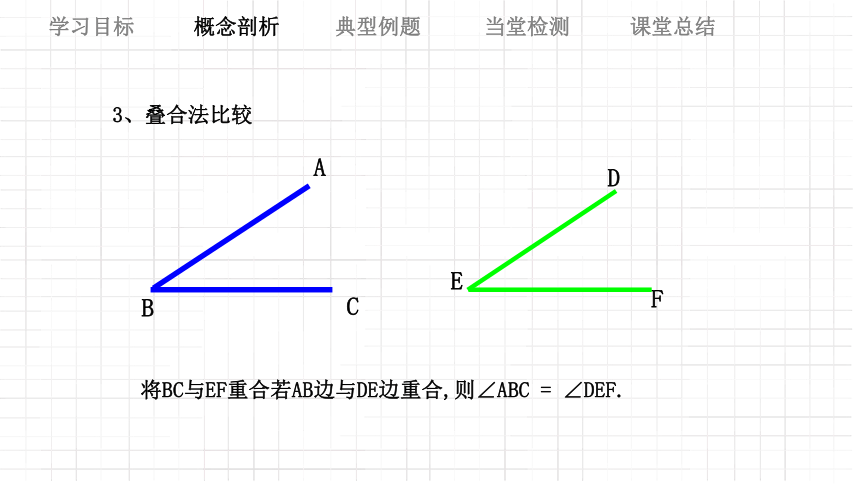
3、叠合法比较
将BC与EF重合若AB边与DE边重合,则∠ABC = ∠DEF.
B
C
A
E
D
F
典型例题
当堂检测
学习目标
课堂总结
概念剖析
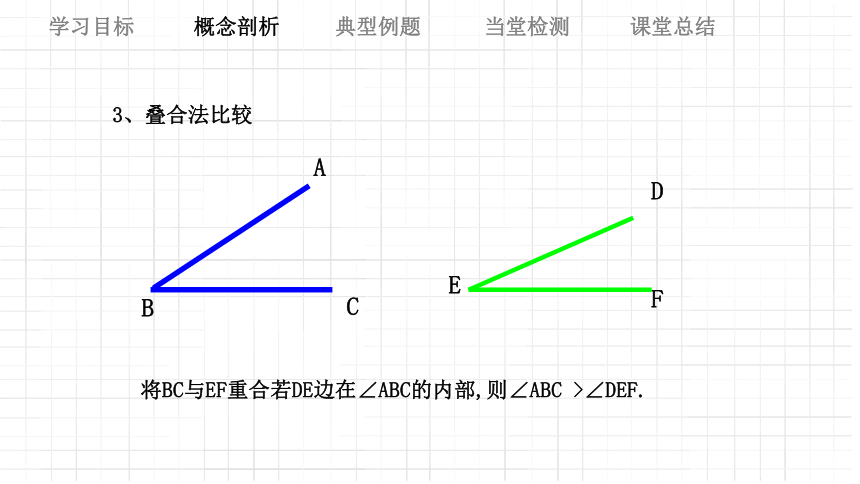
3、叠合法比较
将BC与EF重合若DE边在∠ABC的内部,则∠ABC >∠DEF.
B
C
A
E
D
F
典型例题
当堂检测
学习目标
课堂总结
概念剖析
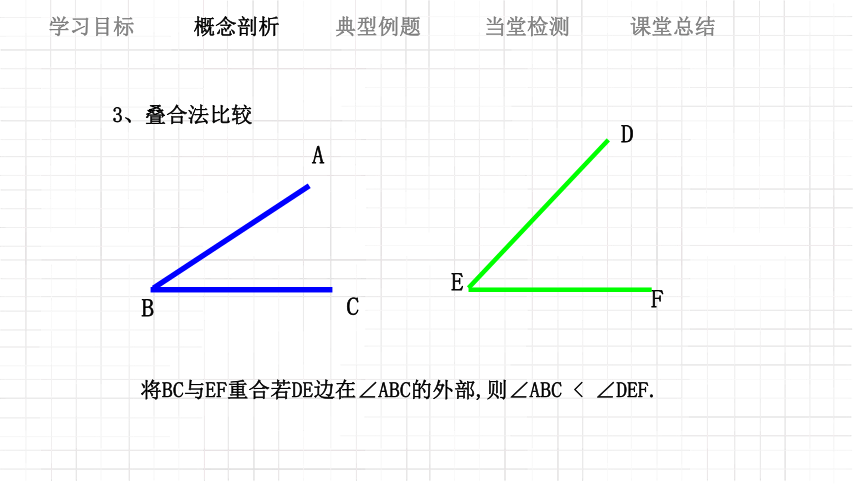
3、叠合法比较
将BC与EF重合若DE边在∠ABC的外部,则∠ABC < ∠DEF.
B
C
A
E
D
F
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(二)角的和差
顶点与一边重合
2
C
B
O
1
O
A
B
O
B
C
2
A
1
B
O
∠AOC为∠1 和∠2 的和
记作:∠AOC =∠1 +∠2
∠AOC为∠1 和∠2 的差
记作:∠AOC =∠1 -∠2
如图,如果∠AOB=∠BOC,那么
∠AOC=2∠AOB=2∠BOC ,
∠AOB=∠BOC= ∠AOC.
我们把射线OB叫做∠AOC的角平分线.
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫这个角的平分线.
(三)角的平分线
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例1.图中共有几个角?它们之间有什么关系?
解:有三个角,关系是:
∠BOC是 ∠AOC与 ∠AOB的差,记作 ∠BOC=∠AOC-∠AOB.
∠AOC是∠AOB与 ∠BOC的和,记作 ∠AOC=∠AOB+∠BOC,
∠AOB是 ∠AOC与 ∠BOC的差,记作 ∠AOB=∠AOC-∠BOC,
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.用一个放大镜去观察一个角的大小,正确的说法是( )
A.角的度数扩大了 B.角的度数缩小了
C.角的度数没有变化 D.以上都不对
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.在∠AOB的内部任取一点C,作射线OC,则一定存在( )
A.∠AOB>∠AOC B.∠AOB<∠BOC
C.∠BOC>∠AOC D.∠AOC>∠BOC
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3.如图,已知∠AOC=67°,∠BOC=22°,求∠AOB的度数.
解: 因为 ∠AOC=67°,∠BOC=22°,
所以∠AOB=∠AOC-∠BOC
=67°- 22°
=45°.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例2.如图,OC平分∠AOD,∠BOD=2∠AOB.若∠AOD=114°,
求∠BOC的度数.
A
B
C
D
O
解:因为∠AOD=∠AOB+∠BOD=114°
∠BOD=2∠AOB
因为OC平分∠AOD
所以∠BOC=∠AOC-∠AOB
=57°-38°
=19°
典型例题
当堂检测
学习目标
课堂总结
概念剖析
所以∠AOB= ∠AOD=38°
所以∠AOC= ∠AOD=57°
标点
解:因为ON平分∠AOC,
因为 OM平分∠BOC,
所以∠MON=∠CON+∠COM
=15°+30°=45°.
所以∠CON= ∠AOC= ×30°=15°,
所以∠COM= ∠BOC= ×60°=30°,
典型例题
当堂检测
学习目标
课堂总结
概念剖析
4.已知:如图∠AOC=30°,∠COB=60°,ON、OM分别平分∠AOC、∠BOC,求∠MON的度数.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
角的比较
度量法
叠合法
角的运算
角的和差倍分关系
角的平分线
角的计算
加与减
乘与除
目测法呢
8.2 角的比较
1.会用“度量法”和“叠合法”比较角的大小;
2.理解角的和、差、倍、分,会进行角的加、减、倍、分运算;
3.理解平分线的概念,会运用角平分线进行有关的运算.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
复习导入
1. 如图,已知线段AB、CD,你有哪些办法比较它们的长短?
1.目测法
2.度量法
3.叠合法
思考:类比线段大小的比较,你认为该如何比较两个角的大小?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(一)角的大小比较
1、目测法
2、度量法
量角器量角要注意:
①对中;②重合;③读数
A
B
70°
C
F
E
D
30°
∠ABC >∠DEF
度数无动画
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3、叠合法比较
将BC与EF重合若AB边与DE边重合,则∠ABC = ∠DEF.
B
C
A
E
D
F
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3、叠合法比较
将BC与EF重合若DE边在∠ABC的内部,则∠ABC >∠DEF.
B
C
A
E
D
F
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3、叠合法比较
将BC与EF重合若DE边在∠ABC的外部,则∠ABC < ∠DEF.
B
C
A
E
D
F
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(二)角的和差
顶点与一边重合
2
C
B
O
1
O
A
B
O
B
C
2
A
1
B
O
∠AOC为∠1 和∠2 的和
记作:∠AOC =∠1 +∠2
∠AOC为∠1 和∠2 的差
记作:∠AOC =∠1 -∠2
如图,如果∠AOB=∠BOC,那么
∠AOC=2∠AOB=2∠BOC ,
∠AOB=∠BOC= ∠AOC.
我们把射线OB叫做∠AOC的角平分线.
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫这个角的平分线.
(三)角的平分线
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例1.图中共有几个角?它们之间有什么关系?
解:有三个角,关系是:
∠BOC是 ∠AOC与 ∠AOB的差,记作 ∠BOC=∠AOC-∠AOB.
∠AOC是∠AOB与 ∠BOC的和,记作 ∠AOC=∠AOB+∠BOC,
∠AOB是 ∠AOC与 ∠BOC的差,记作 ∠AOB=∠AOC-∠BOC,
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.用一个放大镜去观察一个角的大小,正确的说法是( )
A.角的度数扩大了 B.角的度数缩小了
C.角的度数没有变化 D.以上都不对
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.在∠AOB的内部任取一点C,作射线OC,则一定存在( )
A.∠AOB>∠AOC B.∠AOB<∠BOC
C.∠BOC>∠AOC D.∠AOC>∠BOC
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3.如图,已知∠AOC=67°,∠BOC=22°,求∠AOB的度数.
解: 因为 ∠AOC=67°,∠BOC=22°,
所以∠AOB=∠AOC-∠BOC
=67°- 22°
=45°.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例2.如图,OC平分∠AOD,∠BOD=2∠AOB.若∠AOD=114°,
求∠BOC的度数.
A
B
C
D
O
解:因为∠AOD=∠AOB+∠BOD=114°
∠BOD=2∠AOB
因为OC平分∠AOD
所以∠BOC=∠AOC-∠AOB
=57°-38°
=19°
典型例题
当堂检测
学习目标
课堂总结
概念剖析
所以∠AOB= ∠AOD=38°
所以∠AOC= ∠AOD=57°
标点
解:因为ON平分∠AOC,
因为 OM平分∠BOC,
所以∠MON=∠CON+∠COM
=15°+30°=45°.
所以∠CON= ∠AOC= ×30°=15°,
所以∠COM= ∠BOC= ×60°=30°,
典型例题
当堂检测
学习目标
课堂总结
概念剖析
4.已知:如图∠AOC=30°,∠COB=60°,ON、OM分别平分∠AOC、∠BOC,求∠MON的度数.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
角的比较
度量法
叠合法
角的运算
角的和差倍分关系
角的平分线
角的计算
加与减
乘与除
目测法呢
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
