7.8 实数 第1课时 课件(共15张PPT) 青岛版数学八年级下册
文档属性
| 名称 | 7.8 实数 第1课时 课件(共15张PPT) 青岛版数学八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 14:03:50 | ||
图片预览






文档简介
(共15张PPT)
第七章 实数
7.8 实数
第1课时
1.了解实数的概念,会对实数进行分类.
2.能求实数的相反数和绝对值.
3.知道实数与数轴上的点一一对应,会比较两个实数的大小.
知识回顾
1.什么是有理数?有理数怎样分类?
2.什么是无理数?带根号的数都是无理数吗?
无理数是无限不循环小数.
带根号的数不一定是无理数.
整数
分数
有理数
正有理数
负有理数
有理数
0
实数的概念:有理数和无理数统称为实数.
活动:小组合作讨论,完成下列问题.
任务一:对实数进行分类.
问题:请你按照不同的分类标准对实数进行分类.
有理数
无理数
实数
正无理数
负无理数
正有理数
负有理数
零
有限小数或无限循环小数
无限不循环小数
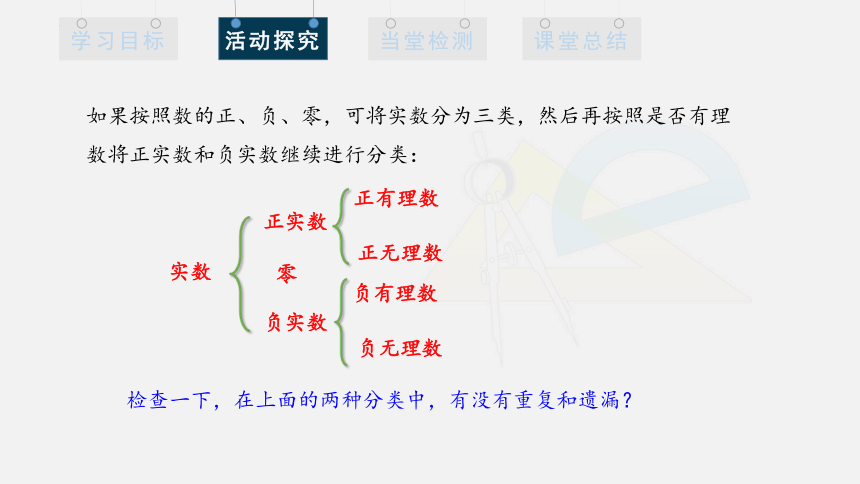
如果按照数的正、负、零,可将实数分为三类,然后再按照是否有理数将正实数和负实数继续进行分类:
正有理数
正无理数
负有理数
负无理数
实数
正实数
负实数
零
检查一下,在上面的两种分类中,有没有重复和遗漏?
将下列各数分别填入下列相应的括号内.
有理数:{ }
无理数:{ }
负数:{ }
正数:{ }
进行分类时,应先对某些实数进行计算或化简,根据最后的结果分类.
练一练
1.5的相反数是 ,绝对值是 .
活动:和同伴一起交流,完成下列填空.
-1.5
1.5
的相反数是 ,绝对值是 .
的相反数是 ,绝对值是 .
思考:通过上述问题,你发现了什么?
任务二:求实数的相反数和绝对值.
把有理数扩充到实数以后,相反数、绝对值的意义也同样适用.
活动小结
数a的相反数是-a.
a(a>0)
0(a=0)
-a(a<0)
|a|=
一个正实数的绝对值是它本身;
一个负实数的绝对值是它的相反数;
0的绝对值是0.
活动1:每个有理数都可以用数轴上的点来表示,那么,无理数呢?带着该疑问,回答下面的问题.
0
1
3
2
4
O'
C=π
点O'对应的数就是π.
问题提出:直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达点O',点O'对应的数是多少?
任务三:知道实数与数轴上的点一一对应,会比较两个实数的大小.
每一个实数都可以用数轴上唯一的一个点来表示;反过来,数轴上的每一个点都表示一个实数.也就是说,实数与数轴上的点一一对应.
数轴上的任意两点,右边的点表示的实数比左边的点表示的实数大.如果a是实数,那么 就是表示数a的点到原点的距离.
原点
0
正实数
负实数
<
活动小结
(1)3.14与π; (2) 与 .
解:(1)∵π ≈ 3.141, ∴3.14 < π.
(2)∵ ≈ -1.732, ≈ -1.442.
∴ < .
活动2:比较下列各组数中两个数的大小.
1.把下列各数填入相应的集合内.
(1)有理数集合:{ };
(2)无理数集合:{ }.
2.求下列各数的相反数和绝对值:
;
;
(2)∵ =-2,
解:(1)
的相反数是 ,绝对值是 .
∴ 的相反数是2,绝对值是2.
(3)∵ =7,
∴ 的相反数是-7,绝对值是7.
3.比较下列各组数里两个数的大小.
(1) ,–1.4; (2) , .
解:(1)∵ ,又 – 1 .414 < – 1.4, 故 .
(2)∵ ,
故 .
针对本课关键词“实数”,说说你学到了什么?
实数
有理数和无理数统称实数.
把有理数扩充到实数以后,相反数、绝对值的意义也同样适用.
实数与数轴上点的一一对应.
第七章 实数
7.8 实数
第1课时
1.了解实数的概念,会对实数进行分类.
2.能求实数的相反数和绝对值.
3.知道实数与数轴上的点一一对应,会比较两个实数的大小.
知识回顾
1.什么是有理数?有理数怎样分类?
2.什么是无理数?带根号的数都是无理数吗?
无理数是无限不循环小数.
带根号的数不一定是无理数.
整数
分数
有理数
正有理数
负有理数
有理数
0
实数的概念:有理数和无理数统称为实数.
活动:小组合作讨论,完成下列问题.
任务一:对实数进行分类.
问题:请你按照不同的分类标准对实数进行分类.
有理数
无理数
实数
正无理数
负无理数
正有理数
负有理数
零
有限小数或无限循环小数
无限不循环小数
如果按照数的正、负、零,可将实数分为三类,然后再按照是否有理数将正实数和负实数继续进行分类:
正有理数
正无理数
负有理数
负无理数
实数
正实数
负实数
零
检查一下,在上面的两种分类中,有没有重复和遗漏?
将下列各数分别填入下列相应的括号内.
有理数:{ }
无理数:{ }
负数:{ }
正数:{ }
进行分类时,应先对某些实数进行计算或化简,根据最后的结果分类.
练一练
1.5的相反数是 ,绝对值是 .
活动:和同伴一起交流,完成下列填空.
-1.5
1.5
的相反数是 ,绝对值是 .
的相反数是 ,绝对值是 .
思考:通过上述问题,你发现了什么?
任务二:求实数的相反数和绝对值.
把有理数扩充到实数以后,相反数、绝对值的意义也同样适用.
活动小结
数a的相反数是-a.
a(a>0)
0(a=0)
-a(a<0)
|a|=
一个正实数的绝对值是它本身;
一个负实数的绝对值是它的相反数;
0的绝对值是0.
活动1:每个有理数都可以用数轴上的点来表示,那么,无理数呢?带着该疑问,回答下面的问题.
0
1
3
2
4
O'
C=π
点O'对应的数就是π.
问题提出:直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达点O',点O'对应的数是多少?
任务三:知道实数与数轴上的点一一对应,会比较两个实数的大小.
每一个实数都可以用数轴上唯一的一个点来表示;反过来,数轴上的每一个点都表示一个实数.也就是说,实数与数轴上的点一一对应.
数轴上的任意两点,右边的点表示的实数比左边的点表示的实数大.如果a是实数,那么 就是表示数a的点到原点的距离.
原点
0
正实数
负实数
<
活动小结
(1)3.14与π; (2) 与 .
解:(1)∵π ≈ 3.141, ∴3.14 < π.
(2)∵ ≈ -1.732, ≈ -1.442.
∴ < .
活动2:比较下列各组数中两个数的大小.
1.把下列各数填入相应的集合内.
(1)有理数集合:{ };
(2)无理数集合:{ }.
2.求下列各数的相反数和绝对值:
;
;
(2)∵ =-2,
解:(1)
的相反数是 ,绝对值是 .
∴ 的相反数是2,绝对值是2.
(3)∵ =7,
∴ 的相反数是-7,绝对值是7.
3.比较下列各组数里两个数的大小.
(1) ,–1.4; (2) , .
解:(1)∵ ,又 – 1 .414 < – 1.4, 故 .
(2)∵ ,
故 .
针对本课关键词“实数”,说说你学到了什么?
实数
有理数和无理数统称实数.
把有理数扩充到实数以后,相反数、绝对值的意义也同样适用.
实数与数轴上点的一一对应.
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
