2015(秋)北师大版九年级数学上册课时集训:13 正方形的性质与判定试卷(共3份附答案)
文档属性
| 名称 | 2015(秋)北师大版九年级数学上册课时集训:13 正方形的性质与判定试卷(共3份附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 172.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-15 17:27:16 | ||
图片预览


文档简介
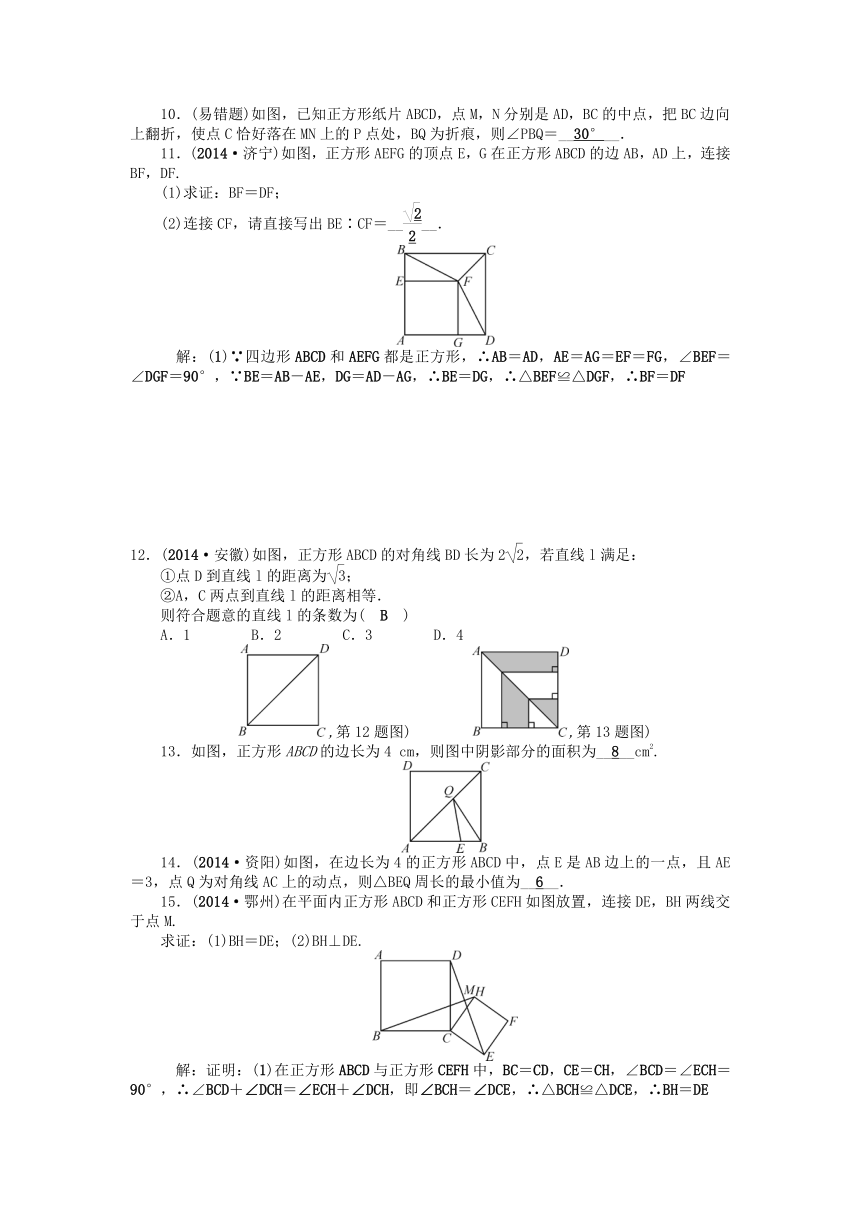
1.3 正方形的性质与判定
第1课时 正方形的性质
1.有一组邻边__相等__,并且有一个角是__直角__的平行四边形叫做正方形.
2.正方形的四个角都是__直角__,四条边__相等__,对角线__相等__且__互相垂直平分__.
知识点一:正方形的定义
1.在四边形ABCD中,若AD∥BC,AD=BC,AB=BC,∠B=90°,则四边形ABCD的形状是( D )
A.平行四边形 B.矩形
C.菱形 D.正方形
2.如图,∠ACB=90°,CD平分∠ACB,DE⊥AC于点E,DF⊥BC于点F,那么四边形DECF是__正方形__.
知识点二:正方形的性质
3.(2014·泉州)正方形的对称轴的条数为( D )
A.1 B.2 C.3 D.4
4.正方形具有而菱形不一定具有的性质是( B )
A.对角线互相平分 B.对角线相等
C.对角线互相垂直 D.对角线平分一组对角
5.(2014·福州)如图,在正方形ABCD的外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( C )
A.45° B.55° C.60° D.75°
,第5题图) ,第6题图)
6.如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连接BD并延长交EG于点T,交FG于点P,则GT=( B )
A. B.2 C.2 D.1
7.(2014·苏州)已知正方形ABCD的对角线AC=,则正方形ABCD的周长是__4__.
8.如图,正方形ABCD的对角线AC与BD相交于点O,则图中共有__8__个等腰直角三角形.
,第8题图) ,第9题图)
9.如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,则∠BCE的度数是__22.5°__.
10.(易错题)如图,已知正方形纸片AB ( http: / / www.21cnjy.com )CD,点M,N分别是AD,BC的中点,把BC边向上翻折,使点C恰好落在MN上的P点处,BQ为折痕,则∠PBQ=__30°__.
11.(2014·济宁)如图,正方形AEFG的顶点E,G在正方形ABCD的边AB,AD上,连接BF,DF.
(1)求证:BF=DF;
(2)连接CF,请直接写出BE∶CF=____.
解:(1)∵四边形ABCD和AEFG都是 ( http: / / www.21cnjy.com )正方形,∴AB=AD,AE=AG=EF=FG,∠BEF=∠DGF=90°,∵BE=AB-AE,DG=AD-AG,∴BE=DG,∴△BEF≌△DGF,∴BF=DF
12.(2014·安徽)如图,正方形ABCD的对角线BD长为2,若直线l满足:
①点D到直线l的距离为;
②A,C两点到直线l的距离相等.
则符合题意的直线l的条数为( B )
A.1 B.2 C.3 D.4
,第12题图) ,第13题图)
13.如图,正方形ABCD的边长为4 cm,则图中阴影部分的面积为__8__cm2.
14.(2014·资阳)如图,在边长为4的 ( http: / / www.21cnjy.com )正方形ABCD中,点E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,则△BEQ周长的最小值为__6__.
15.(2014·鄂州)在平面内正方形ABCD和正方形CEFH如图放置,连接DE,BH两线交于点M.
求证:(1)BH=DE;(2)BH⊥DE.
解:证明:(1)在正方形 ( http: / / www.21cnjy.com )ABCD与正方形CEFH中,BC=CD,CE=CH,∠BCD=∠ECH=90°,∴∠BCD+∠DCH=∠ECH+∠DCH,即∠BCH=∠DCE,∴△BCH≌△DCE,∴BH=DE
(2)由(1)得,∠CBH=∠CDE,∴∠DMB=∠BCD=90°,∴BH⊥DE
16.(教材例4改编)已知:如图,在△ ( http: / / www.21cnjy.com )ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.
(1)四边形ADCE为__矩形__;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
解:(2)当△ABC满足∠BAC ( http: / / www.21cnjy.com )=90°时,四边形ADCE是一个正方形,.理由:∵AB=AC,∴∠ACB=∠B=45°,∵AD⊥BC,∴∠CAD=∠ACD=45°,∴DC=AD,∵四边形ADCE为矩形,∴矩形ADCE是正方形,∴当∠BAC=90°时,四边形ADCE是一个正方形
17.将正方形(图①)作如下操作: ( http: / / www.21cnjy.com )第1次:分别连接各边中点(如图②),得到5个正方形;第2次:将图②左上角正方形按上述方法再分割(如图③),得到9个正方形……,以此类推,根据以上操作,若要得到2013个正方形,则需要操作的次数是( B )
A.502 B.503 C.504 D.505
18.如图所示,在正方形ABCD中,点E,F ( http: / / www.21cnjy.com )分别在BC,CD上移动,但点A到EF的距离AH始终保持与AB的长度相等,问在点E,F移动过程中:
(1)∠EAF的大小是否发生变化?请说明理由;
(2)△ECF的周长是否发生变化?请说明理由.
解:(1)∠EAF的大小 ( http: / / www.21cnjy.com )不变,理由如下:在正方形ABCD中,∵AH⊥EF,∴∠AHF=∠D=90°.∵AF=AF,AH=AD,∴Rt△AHF≌Rt△ADF(HL).∴∠HAF=∠DAF.同理 ∠HAE=∠BAE.∵∠HAF+∠DAF+∠HAE+∠BAE=90°,∴∠EAF=∠HAF+∠HAE=45°.∴∠EAF的大小不会发生变化 (2)△ECF的周长不会发生变化,理由如下:由(1)知:Rt△AHF≌Rt△ADF,Rt△AHE≌Rt△ABE,∴FH=FD,EH=EB.∴EF=EH+FH=EB+FD.∴CE+CF+EF=CE+CF+EB+FD=BC+CD.∴△ECF的周长总等于正方形ABCD边长的2倍,不会发生变化
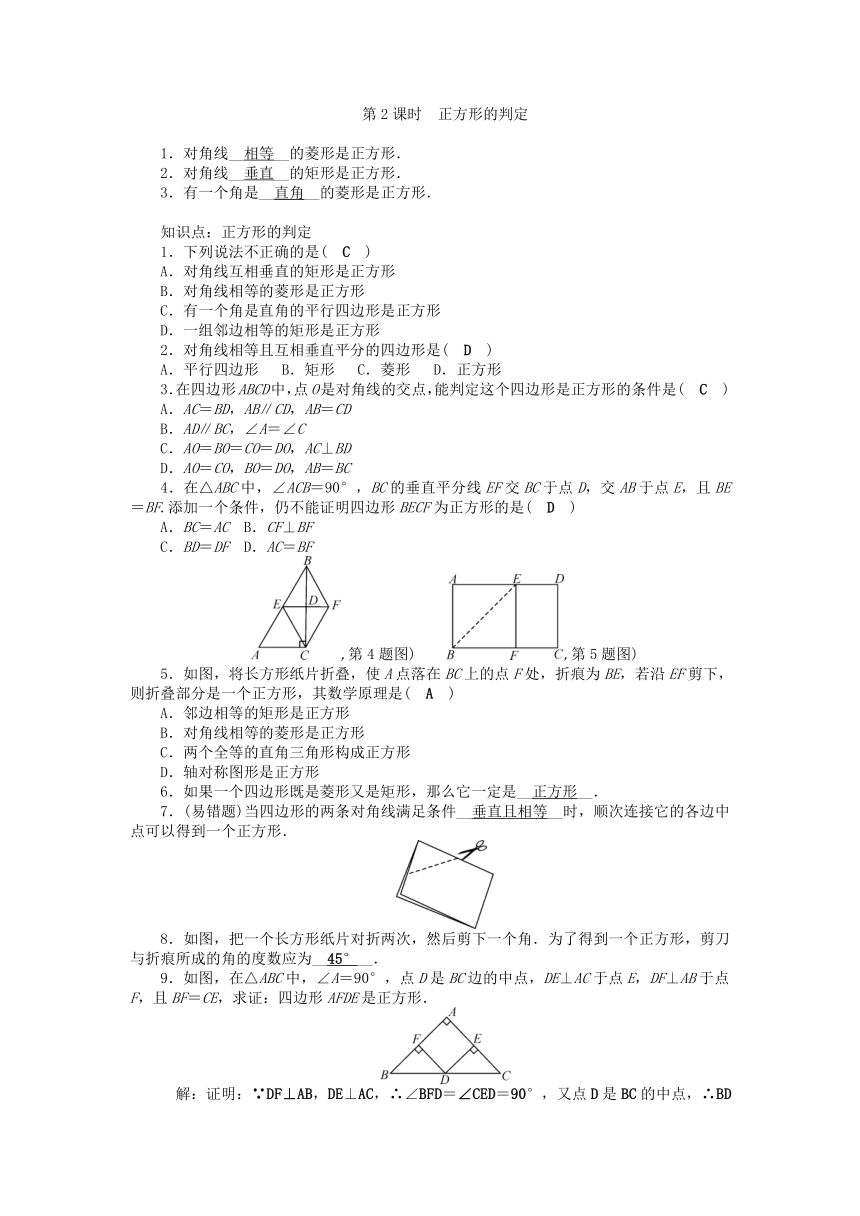
第2课时 正方形的判定
1.对角线__相等__的菱形是正方形.
2.对角线__垂直__的矩形是正方形.
3.有一个角是__直角__的菱形是正方形.
知识点:正方形的判定
1.下列说法不正确的是( C )
A.对角线互相垂直的矩形是正方形
B.对角线相等的菱形是正方形
C.有一个角是直角的平行四边形是正方形
D.一组邻边相等的矩形是正方形
2.对角线相等且互相垂直平分的四边形是( D )
A.平行四边形 B.矩形 C.菱形 D.正方形
3.在四边形ABCD中,点O是对角线的交点,能判定这个四边形是正方形的条件是( C )
A.AC=BD,AB∥CD,AB=CD
B.AD∥BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD
D.AO=CO,BO=DO,AB=BC
4.在△ABC中,∠AC ( http: / / www.21cnjy.com )B=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF.添加一个条件,仍不能证明四边形BECF为正方形的是( D )
A.BC=AC B.CF⊥BF
C.BD=DF D.AC=BF
,第4题图) ,第5题图)
5.如图,将长方形纸片折叠,使A点落在BC上的点F处,折痕为BE,若沿EF剪下,则折叠部分是一个正方形,其数学原理是( A )
A.邻边相等的矩形是正方形
B.对角线相等的菱形是正方形
C.两个全等的直角三角形构成正方形
D.轴对称图形是正方形
6.如果一个四边形既是菱形又是矩形,那么它一定是__正方形__.
7.(易错题)当四边形的两条对角线满足条件__垂直且相等__时,顺次连接它的各边中点可以得到一个正方形.
8.如图,把一个长方形纸片对折两次,然后剪下一个角.为了得到一个正方形,剪刀与折痕所成的角的度数应为__45°__.
9.如图,在△ABC中,∠A=90°,点D是BC边的中点,DE⊥AC于点E,DF⊥AB于点F,且BF=CE,求证:四边形AFDE是正方形.
解:证明:∵DF⊥AB,DE⊥AC, ( http: / / www.21cnjy.com )∴∠BFD=∠CED=90°,又点D是BC的中点,∴BD=CD,∵BF=CE,∴△BFD≌△CED(HL).∴DF=DE,∵∠A=∠AFD=∠AED=90°,∴四边形AFDE为矩形,∵DF=DE,∴矩形AFDE是正方形
10.(2014·株州)已知四边形AB ( http: / / www.21cnjy.com )CD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD.四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( B )
A.选①② B.选②③ C.选①③ D.选②④
11.如图,在Rt△ABC中,∠A ( http: / / www.21cnjy.com )CB=90°,点D,E,F分别是AB,AC,BC的中点,连接DE,DF,EF,要使四边形DECF是正方形,只需增加一个条件为__AC=BC__.
12.小明想检查一个四边形的框架是不是正方形,但手头仅有一把卷尺.你能帮他设计一个检查方案吗?说说你的做法和理由.
解:方法:测量四边形的框架的四边长及四 ( http: / / www.21cnjy.com )边形的框架的对角线长;理由:若四边形的框架满足四边长相等,则是菱形,若再满足对角线相等,则是正方形,否则不是
13.如图,在平面直角坐标系中,四边 ( http: / / www.21cnjy.com )形ABCD的顶点坐标分别是A(-2,0),B(0,-2),C(2,0),D(0,2),求证:四边形ABCD是正方形.
解:证明:由四边形ABCD的顶点坐标 ( http: / / www.21cnjy.com )分别是A(-2,0),B(0,-2),C(2,0),D(0,2),可知OA=OB=OC=OD=2,∴四边形ABCD为矩形.∵AC⊥BD,∴四边形ABCD是正方形
14.如图,在Rt△ABC中, ( http: / / www.21cnjy.com )∠BAC=90°,AD=CD,点E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC交DE于点G,连接AF,CG.
(1)求证:AF=BF;
(2)如果AB=AC,求证:四边形AFCG是正方形.
解:(1)证明:∵AD=CD,点E是 ( http: / / www.21cnjy.com )边AC的中点, ∴DE⊥AC,即DE垂直平分线段AC,∴∠FAC=∠ACB.在Rt△ACB中,由∠BAC=90°,得∠B+∠ACB=90°,∠FAC+∠BAF=90°,∴∠B=∠BAF,∴AF=BF (2)∵AG∥CF,∴∠AGE=∠CFE.又∵点E是边AC的中点,∴AE=CE.又∠AEG=∠CEF,∴△AEG≌△CEF(AAS),∴AG=CF.又∵AG∥CF,∴四边形AFCG是平行四边形.∵AF=CF,∴四边形AFCG是菱形.在Rt△ABC中,由AF=CF,AF=BF,得BF=CF,又∵AB=AC,∴AF⊥BC,即∠AFC=90°,∴四边形AFCG是正方形
15.(2014·随州)已知:如图,在矩形ABCD中,点M,N分别是AD,BC的中点,点E,F分别是线段BM,CM的中点.
(1)求证:△ABM≌△DCM;
(2)填空:当AB∶AD=__1∶2__时,四边形MENF是正方形,并说明理由.
解:(1)证明:∵四边形ABCD是矩形, ( http: / / www.21cnjy.com )∴AB=DC,∠A=∠D=90°,又∵点M为AD的中点,∴AM=DM,在△ABM和△DCM中,∴△ABM≌△DCM(SAS) (2)当AB∶AD=1∶2时,四边形MENF是正方形,理由是:∵AB∶AD=1∶2,AM=DM,AB=CD,∴AB=AM=DM=DC,∵∠A=∠D=90°,∴∠ABM=∠AMB=∠DMC=∠DCM=45°,∴∠MBC=∠MCB=45°,∴BM=CM,∠BMC=90°,∵点N,E,F分别是BC,BM,CM的中点,∴BE=CF=ME=MF,NF∥BM,NE∥CM,∴四边形MENF是平行四边形,∵ME=MF,∠BMC=90°,∴四边形MENF是正方形,即当AB∶AD=1∶2时,四边形MENF是正方形
专题(一) 特殊平行四边形的性质与判定
一、特殊平行四边形与折叠
1.如图,矩形纸片ABCD, ( http: / / www.21cnjy.com )AB=2,∠ADB=30°,沿对角线BD折叠(使△ABD和△EBD落在同一平面内),则A,E两点间的距离为__2__.
,第1题图) ,第2题图)
2.(2014·龙东)如图,菱形ABC ( http: / / www.21cnjy.com )D中,对角线AC=6,BD=8,点M,N分别是BC,CD的中点,点P是线段BD上的一个动点,则PM+PN的最小值是__5__.
3.(2014·绥化)矩形纸片ABCD ( http: / / www.21cnjy.com )中,已知AD=8,AB=6,点E是边BC上的点,以AE为折痕折叠纸片,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为__3或6__.
二、特殊平行四边形的判定与性质
4.(2014·厦门)如图,在四边形AB ( http: / / www.21cnjy.com )CD中,AD∥BC,AM⊥BC,垂足为点M,AN⊥DC,垂足为点N,若∠BAD=∠BCD,AM=AN,求证:四边形ABCD是菱形.
解:证明:∵AD∥BC,∴∠B+∠BAD= ( http: / / www.21cnjy.com )180°,∠D+∠C=180°,∵∠BAD=∠BCD,∴∠B=∠D,∴四边形ABCD是平行四边形,∵AM⊥BC,AN⊥DC,∴∠AMB=∠AND=90°,又AM=AN,可证得△ABM≌△ADN,∴AB=AD,∴四边形ABCD是菱形
5.(2014·枣庄)如图,四边形ABCD对角线AC,BD交于点O,已知点O是AC的中点,AE=CF,DF∥BE.
(1)求证:△BOE≌△DOF;
(2)若OD=AC,则四边形ABCD是什么特殊四边形?请证明你的结论.
解:(1)证明:∵DF∥BE,∴∠ ( http: / / www.21cnjy.com )FDO=∠EBO,∠DFO=∠BEO,∵点O为AC的中点,即OA=OC,AE=CF,∴OA-AE=OC-CF,即OE=OF,在△BOE和△DOF中,∴△BOE≌△DOF(AAS) (2)若OD=AC,则四边形ABCD是矩形,理由:∵△BOE≌△DOF,∴OB=OD.∴四边形ABCD为平行四边形.∵OD=AC,∴OA=OB=OC=OD,即BD=AC,∴四边形ABCD为矩形
6.如图,四边形ABCD是正方形,点G是BC边上的任意一点,DE⊥AG,BF∥DE交AG于点F.
(1)求证:AF-BF=EF;
(2)将△ABF绕点A逆时针旋转,使得AB与AD重合,记此时点F的对应点为点F′.若正方形边长为3,求点F′与旋转前的图中点E之间的距离.
解:(1)易证△AED≌△BFA,∴BF=AE,∵AF-AE=EF,∴AF-BF=EF
(2)如图,根据题意知,∠FAF′=9 ( http: / / www.21cnjy.com )0°,DE=AF=AF′,∴∠F′AE=∠AED=90°,∴∠F′AE+∠AED=180°,∴A′F∥ED,∴四边形AEDF′为平行四边形.又∠AED=90°,∴四边形AEDF′是矩形,∴EF′=AD=3
三、特殊平行四边形与探究
7.如图,在菱形ABCD中,AB=2,∠ ( http: / / www.21cnjy.com )DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.
(1)求证:四边形AMDN是平行四边形;
(2)填空:
①当AM的值为__1__时,四边形AMDN是矩形;
②当AM的值为__2__时,四边形AMDN是菱形.
解:(1)证明:∵四边形ABCD ( http: / / www.21cnjy.com )是菱形,∴ND∥AM,∴∠NDE=∠MAE,∠DNE=∠AME.又∵点E是AD边的中点,∴DE=AE,∴△NDE≌△MAE,∴ND=MA.又∵ND∥MA,∴四边形AMDN是平行四边形
8.如图,△ABC是等腰直角三角形,∠BAC=90°,点P,Q分别是AB,AC上的动点,且满足BP=AQ,点D是BC的中点.
(1)求证:△PDQ是等腰直角三角形;
(2)当点P运动到什么位置时,四边形APDQ是正方形,并说明理由.
解:(1)证明:连接AD.∵△AB ( http: / / www.21cnjy.com )C是等腰直角三角形,点D是BC的中点,∴AD⊥BC,AD=BD=DC,∠DAQ=∠B.又∵BP=AQ,∴△BPD≌△AQD.∴PD=QD,∠ADQ=∠BDP.∵∠BDP+∠ADP=90°,∴∠ADQ+∠ADP=∠PDQ=90°.∴△PDQ为等腰直角三角形 (2)当点P运动到AB的中点时,四边形APDQ是正方形.理由:由(1)知△ABD为等腰直角三角形.当点P为AB的中点时,DP⊥AB,即∠APD=90°.又∵∠A=90°,∠PDQ=90°,∴四边形APDQ为矩形.又∵DP=AP=AB,∴四边形APDQ为正方形
9.(2014·日照)
(1)如图①,在正方形ABCD中,点E是AB上一点,点F是AD延长线上一点,且DF=BE.
求证:CE=CF;
(2)如图②,在正方形ABCD中,点E是AB上一点,点G是AD上一点,如果∠GCE=45°,请你利用(1)的启示证明:GE=BE+GD;
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图③,在四边形ABCD中,AD∥BC ( http: / / www.21cnjy.com )(BC>AD),∠B=90°,AB=BC,点E是AB上一点,且∠DCE=45°,BE=4,AE=8,DE=10,求四边形ABCD的面积.
解:(1)略
(2)证明:如图②,延长AD ( http: / / www.21cnjy.com )至点F,使DF=BE.连接CF.由(1)知△CBE≌△CDF,∴∠BCE=∠DCF.∴∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90°,又∵∠GCE=45°,∴∠GCF=∠GCE=45°.∵CE=CF,∠GCE=∠GCF,GC=GC,∴△ECG≌△FCG.∴GE=GF,∴GE=DF+GD=BE+GD (3)如图③,过点C作CG⊥AD,交AD延长线于点G.∵AD∥BC,∴∠A=∠B=90°,又∠CGA=90°,AB=BC,∴四边形ABCG为正方形.∴AG=BC.已知∠DCE=45°,根据(1)(2)可知,ED=BE+DG.所以10=4+DG,即DG=6,AD=12-6=6,所以四边形ABCD的面积为S=(AD+BC)·AB=×(6+12)×12=108.答:四边形ABCD的面积为108
第1课时 正方形的性质
1.有一组邻边__相等__,并且有一个角是__直角__的平行四边形叫做正方形.
2.正方形的四个角都是__直角__,四条边__相等__,对角线__相等__且__互相垂直平分__.
知识点一:正方形的定义
1.在四边形ABCD中,若AD∥BC,AD=BC,AB=BC,∠B=90°,则四边形ABCD的形状是( D )
A.平行四边形 B.矩形
C.菱形 D.正方形
2.如图,∠ACB=90°,CD平分∠ACB,DE⊥AC于点E,DF⊥BC于点F,那么四边形DECF是__正方形__.
知识点二:正方形的性质
3.(2014·泉州)正方形的对称轴的条数为( D )
A.1 B.2 C.3 D.4
4.正方形具有而菱形不一定具有的性质是( B )
A.对角线互相平分 B.对角线相等
C.对角线互相垂直 D.对角线平分一组对角
5.(2014·福州)如图,在正方形ABCD的外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( C )
A.45° B.55° C.60° D.75°
,第5题图) ,第6题图)
6.如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连接BD并延长交EG于点T,交FG于点P,则GT=( B )
A. B.2 C.2 D.1
7.(2014·苏州)已知正方形ABCD的对角线AC=,则正方形ABCD的周长是__4__.
8.如图,正方形ABCD的对角线AC与BD相交于点O,则图中共有__8__个等腰直角三角形.
,第8题图) ,第9题图)
9.如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,则∠BCE的度数是__22.5°__.
10.(易错题)如图,已知正方形纸片AB ( http: / / www.21cnjy.com )CD,点M,N分别是AD,BC的中点,把BC边向上翻折,使点C恰好落在MN上的P点处,BQ为折痕,则∠PBQ=__30°__.
11.(2014·济宁)如图,正方形AEFG的顶点E,G在正方形ABCD的边AB,AD上,连接BF,DF.
(1)求证:BF=DF;
(2)连接CF,请直接写出BE∶CF=____.
解:(1)∵四边形ABCD和AEFG都是 ( http: / / www.21cnjy.com )正方形,∴AB=AD,AE=AG=EF=FG,∠BEF=∠DGF=90°,∵BE=AB-AE,DG=AD-AG,∴BE=DG,∴△BEF≌△DGF,∴BF=DF
12.(2014·安徽)如图,正方形ABCD的对角线BD长为2,若直线l满足:
①点D到直线l的距离为;
②A,C两点到直线l的距离相等.
则符合题意的直线l的条数为( B )
A.1 B.2 C.3 D.4
,第12题图) ,第13题图)
13.如图,正方形ABCD的边长为4 cm,则图中阴影部分的面积为__8__cm2.
14.(2014·资阳)如图,在边长为4的 ( http: / / www.21cnjy.com )正方形ABCD中,点E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,则△BEQ周长的最小值为__6__.
15.(2014·鄂州)在平面内正方形ABCD和正方形CEFH如图放置,连接DE,BH两线交于点M.
求证:(1)BH=DE;(2)BH⊥DE.
解:证明:(1)在正方形 ( http: / / www.21cnjy.com )ABCD与正方形CEFH中,BC=CD,CE=CH,∠BCD=∠ECH=90°,∴∠BCD+∠DCH=∠ECH+∠DCH,即∠BCH=∠DCE,∴△BCH≌△DCE,∴BH=DE
(2)由(1)得,∠CBH=∠CDE,∴∠DMB=∠BCD=90°,∴BH⊥DE
16.(教材例4改编)已知:如图,在△ ( http: / / www.21cnjy.com )ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.
(1)四边形ADCE为__矩形__;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
解:(2)当△ABC满足∠BAC ( http: / / www.21cnjy.com )=90°时,四边形ADCE是一个正方形,.理由:∵AB=AC,∴∠ACB=∠B=45°,∵AD⊥BC,∴∠CAD=∠ACD=45°,∴DC=AD,∵四边形ADCE为矩形,∴矩形ADCE是正方形,∴当∠BAC=90°时,四边形ADCE是一个正方形
17.将正方形(图①)作如下操作: ( http: / / www.21cnjy.com )第1次:分别连接各边中点(如图②),得到5个正方形;第2次:将图②左上角正方形按上述方法再分割(如图③),得到9个正方形……,以此类推,根据以上操作,若要得到2013个正方形,则需要操作的次数是( B )
A.502 B.503 C.504 D.505
18.如图所示,在正方形ABCD中,点E,F ( http: / / www.21cnjy.com )分别在BC,CD上移动,但点A到EF的距离AH始终保持与AB的长度相等,问在点E,F移动过程中:
(1)∠EAF的大小是否发生变化?请说明理由;
(2)△ECF的周长是否发生变化?请说明理由.
解:(1)∠EAF的大小 ( http: / / www.21cnjy.com )不变,理由如下:在正方形ABCD中,∵AH⊥EF,∴∠AHF=∠D=90°.∵AF=AF,AH=AD,∴Rt△AHF≌Rt△ADF(HL).∴∠HAF=∠DAF.同理 ∠HAE=∠BAE.∵∠HAF+∠DAF+∠HAE+∠BAE=90°,∴∠EAF=∠HAF+∠HAE=45°.∴∠EAF的大小不会发生变化 (2)△ECF的周长不会发生变化,理由如下:由(1)知:Rt△AHF≌Rt△ADF,Rt△AHE≌Rt△ABE,∴FH=FD,EH=EB.∴EF=EH+FH=EB+FD.∴CE+CF+EF=CE+CF+EB+FD=BC+CD.∴△ECF的周长总等于正方形ABCD边长的2倍,不会发生变化
第2课时 正方形的判定
1.对角线__相等__的菱形是正方形.
2.对角线__垂直__的矩形是正方形.
3.有一个角是__直角__的菱形是正方形.
知识点:正方形的判定
1.下列说法不正确的是( C )
A.对角线互相垂直的矩形是正方形
B.对角线相等的菱形是正方形
C.有一个角是直角的平行四边形是正方形
D.一组邻边相等的矩形是正方形
2.对角线相等且互相垂直平分的四边形是( D )
A.平行四边形 B.矩形 C.菱形 D.正方形
3.在四边形ABCD中,点O是对角线的交点,能判定这个四边形是正方形的条件是( C )
A.AC=BD,AB∥CD,AB=CD
B.AD∥BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD
D.AO=CO,BO=DO,AB=BC
4.在△ABC中,∠AC ( http: / / www.21cnjy.com )B=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF.添加一个条件,仍不能证明四边形BECF为正方形的是( D )
A.BC=AC B.CF⊥BF
C.BD=DF D.AC=BF
,第4题图) ,第5题图)
5.如图,将长方形纸片折叠,使A点落在BC上的点F处,折痕为BE,若沿EF剪下,则折叠部分是一个正方形,其数学原理是( A )
A.邻边相等的矩形是正方形
B.对角线相等的菱形是正方形
C.两个全等的直角三角形构成正方形
D.轴对称图形是正方形
6.如果一个四边形既是菱形又是矩形,那么它一定是__正方形__.
7.(易错题)当四边形的两条对角线满足条件__垂直且相等__时,顺次连接它的各边中点可以得到一个正方形.
8.如图,把一个长方形纸片对折两次,然后剪下一个角.为了得到一个正方形,剪刀与折痕所成的角的度数应为__45°__.
9.如图,在△ABC中,∠A=90°,点D是BC边的中点,DE⊥AC于点E,DF⊥AB于点F,且BF=CE,求证:四边形AFDE是正方形.
解:证明:∵DF⊥AB,DE⊥AC, ( http: / / www.21cnjy.com )∴∠BFD=∠CED=90°,又点D是BC的中点,∴BD=CD,∵BF=CE,∴△BFD≌△CED(HL).∴DF=DE,∵∠A=∠AFD=∠AED=90°,∴四边形AFDE为矩形,∵DF=DE,∴矩形AFDE是正方形
10.(2014·株州)已知四边形AB ( http: / / www.21cnjy.com )CD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD.四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( B )
A.选①② B.选②③ C.选①③ D.选②④
11.如图,在Rt△ABC中,∠A ( http: / / www.21cnjy.com )CB=90°,点D,E,F分别是AB,AC,BC的中点,连接DE,DF,EF,要使四边形DECF是正方形,只需增加一个条件为__AC=BC__.
12.小明想检查一个四边形的框架是不是正方形,但手头仅有一把卷尺.你能帮他设计一个检查方案吗?说说你的做法和理由.
解:方法:测量四边形的框架的四边长及四 ( http: / / www.21cnjy.com )边形的框架的对角线长;理由:若四边形的框架满足四边长相等,则是菱形,若再满足对角线相等,则是正方形,否则不是
13.如图,在平面直角坐标系中,四边 ( http: / / www.21cnjy.com )形ABCD的顶点坐标分别是A(-2,0),B(0,-2),C(2,0),D(0,2),求证:四边形ABCD是正方形.
解:证明:由四边形ABCD的顶点坐标 ( http: / / www.21cnjy.com )分别是A(-2,0),B(0,-2),C(2,0),D(0,2),可知OA=OB=OC=OD=2,∴四边形ABCD为矩形.∵AC⊥BD,∴四边形ABCD是正方形
14.如图,在Rt△ABC中, ( http: / / www.21cnjy.com )∠BAC=90°,AD=CD,点E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC交DE于点G,连接AF,CG.
(1)求证:AF=BF;
(2)如果AB=AC,求证:四边形AFCG是正方形.
解:(1)证明:∵AD=CD,点E是 ( http: / / www.21cnjy.com )边AC的中点, ∴DE⊥AC,即DE垂直平分线段AC,∴∠FAC=∠ACB.在Rt△ACB中,由∠BAC=90°,得∠B+∠ACB=90°,∠FAC+∠BAF=90°,∴∠B=∠BAF,∴AF=BF (2)∵AG∥CF,∴∠AGE=∠CFE.又∵点E是边AC的中点,∴AE=CE.又∠AEG=∠CEF,∴△AEG≌△CEF(AAS),∴AG=CF.又∵AG∥CF,∴四边形AFCG是平行四边形.∵AF=CF,∴四边形AFCG是菱形.在Rt△ABC中,由AF=CF,AF=BF,得BF=CF,又∵AB=AC,∴AF⊥BC,即∠AFC=90°,∴四边形AFCG是正方形
15.(2014·随州)已知:如图,在矩形ABCD中,点M,N分别是AD,BC的中点,点E,F分别是线段BM,CM的中点.
(1)求证:△ABM≌△DCM;
(2)填空:当AB∶AD=__1∶2__时,四边形MENF是正方形,并说明理由.
解:(1)证明:∵四边形ABCD是矩形, ( http: / / www.21cnjy.com )∴AB=DC,∠A=∠D=90°,又∵点M为AD的中点,∴AM=DM,在△ABM和△DCM中,∴△ABM≌△DCM(SAS) (2)当AB∶AD=1∶2时,四边形MENF是正方形,理由是:∵AB∶AD=1∶2,AM=DM,AB=CD,∴AB=AM=DM=DC,∵∠A=∠D=90°,∴∠ABM=∠AMB=∠DMC=∠DCM=45°,∴∠MBC=∠MCB=45°,∴BM=CM,∠BMC=90°,∵点N,E,F分别是BC,BM,CM的中点,∴BE=CF=ME=MF,NF∥BM,NE∥CM,∴四边形MENF是平行四边形,∵ME=MF,∠BMC=90°,∴四边形MENF是正方形,即当AB∶AD=1∶2时,四边形MENF是正方形
专题(一) 特殊平行四边形的性质与判定
一、特殊平行四边形与折叠
1.如图,矩形纸片ABCD, ( http: / / www.21cnjy.com )AB=2,∠ADB=30°,沿对角线BD折叠(使△ABD和△EBD落在同一平面内),则A,E两点间的距离为__2__.
,第1题图) ,第2题图)
2.(2014·龙东)如图,菱形ABC ( http: / / www.21cnjy.com )D中,对角线AC=6,BD=8,点M,N分别是BC,CD的中点,点P是线段BD上的一个动点,则PM+PN的最小值是__5__.
3.(2014·绥化)矩形纸片ABCD ( http: / / www.21cnjy.com )中,已知AD=8,AB=6,点E是边BC上的点,以AE为折痕折叠纸片,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为__3或6__.
二、特殊平行四边形的判定与性质
4.(2014·厦门)如图,在四边形AB ( http: / / www.21cnjy.com )CD中,AD∥BC,AM⊥BC,垂足为点M,AN⊥DC,垂足为点N,若∠BAD=∠BCD,AM=AN,求证:四边形ABCD是菱形.
解:证明:∵AD∥BC,∴∠B+∠BAD= ( http: / / www.21cnjy.com )180°,∠D+∠C=180°,∵∠BAD=∠BCD,∴∠B=∠D,∴四边形ABCD是平行四边形,∵AM⊥BC,AN⊥DC,∴∠AMB=∠AND=90°,又AM=AN,可证得△ABM≌△ADN,∴AB=AD,∴四边形ABCD是菱形
5.(2014·枣庄)如图,四边形ABCD对角线AC,BD交于点O,已知点O是AC的中点,AE=CF,DF∥BE.
(1)求证:△BOE≌△DOF;
(2)若OD=AC,则四边形ABCD是什么特殊四边形?请证明你的结论.
解:(1)证明:∵DF∥BE,∴∠ ( http: / / www.21cnjy.com )FDO=∠EBO,∠DFO=∠BEO,∵点O为AC的中点,即OA=OC,AE=CF,∴OA-AE=OC-CF,即OE=OF,在△BOE和△DOF中,∴△BOE≌△DOF(AAS) (2)若OD=AC,则四边形ABCD是矩形,理由:∵△BOE≌△DOF,∴OB=OD.∴四边形ABCD为平行四边形.∵OD=AC,∴OA=OB=OC=OD,即BD=AC,∴四边形ABCD为矩形
6.如图,四边形ABCD是正方形,点G是BC边上的任意一点,DE⊥AG,BF∥DE交AG于点F.
(1)求证:AF-BF=EF;
(2)将△ABF绕点A逆时针旋转,使得AB与AD重合,记此时点F的对应点为点F′.若正方形边长为3,求点F′与旋转前的图中点E之间的距离.
解:(1)易证△AED≌△BFA,∴BF=AE,∵AF-AE=EF,∴AF-BF=EF
(2)如图,根据题意知,∠FAF′=9 ( http: / / www.21cnjy.com )0°,DE=AF=AF′,∴∠F′AE=∠AED=90°,∴∠F′AE+∠AED=180°,∴A′F∥ED,∴四边形AEDF′为平行四边形.又∠AED=90°,∴四边形AEDF′是矩形,∴EF′=AD=3
三、特殊平行四边形与探究
7.如图,在菱形ABCD中,AB=2,∠ ( http: / / www.21cnjy.com )DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.
(1)求证:四边形AMDN是平行四边形;
(2)填空:
①当AM的值为__1__时,四边形AMDN是矩形;
②当AM的值为__2__时,四边形AMDN是菱形.
解:(1)证明:∵四边形ABCD ( http: / / www.21cnjy.com )是菱形,∴ND∥AM,∴∠NDE=∠MAE,∠DNE=∠AME.又∵点E是AD边的中点,∴DE=AE,∴△NDE≌△MAE,∴ND=MA.又∵ND∥MA,∴四边形AMDN是平行四边形
8.如图,△ABC是等腰直角三角形,∠BAC=90°,点P,Q分别是AB,AC上的动点,且满足BP=AQ,点D是BC的中点.
(1)求证:△PDQ是等腰直角三角形;
(2)当点P运动到什么位置时,四边形APDQ是正方形,并说明理由.
解:(1)证明:连接AD.∵△AB ( http: / / www.21cnjy.com )C是等腰直角三角形,点D是BC的中点,∴AD⊥BC,AD=BD=DC,∠DAQ=∠B.又∵BP=AQ,∴△BPD≌△AQD.∴PD=QD,∠ADQ=∠BDP.∵∠BDP+∠ADP=90°,∴∠ADQ+∠ADP=∠PDQ=90°.∴△PDQ为等腰直角三角形 (2)当点P运动到AB的中点时,四边形APDQ是正方形.理由:由(1)知△ABD为等腰直角三角形.当点P为AB的中点时,DP⊥AB,即∠APD=90°.又∵∠A=90°,∠PDQ=90°,∴四边形APDQ为矩形.又∵DP=AP=AB,∴四边形APDQ为正方形
9.(2014·日照)
(1)如图①,在正方形ABCD中,点E是AB上一点,点F是AD延长线上一点,且DF=BE.
求证:CE=CF;
(2)如图②,在正方形ABCD中,点E是AB上一点,点G是AD上一点,如果∠GCE=45°,请你利用(1)的启示证明:GE=BE+GD;
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图③,在四边形ABCD中,AD∥BC ( http: / / www.21cnjy.com )(BC>AD),∠B=90°,AB=BC,点E是AB上一点,且∠DCE=45°,BE=4,AE=8,DE=10,求四边形ABCD的面积.
解:(1)略
(2)证明:如图②,延长AD ( http: / / www.21cnjy.com )至点F,使DF=BE.连接CF.由(1)知△CBE≌△CDF,∴∠BCE=∠DCF.∴∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90°,又∵∠GCE=45°,∴∠GCF=∠GCE=45°.∵CE=CF,∠GCE=∠GCF,GC=GC,∴△ECG≌△FCG.∴GE=GF,∴GE=DF+GD=BE+GD (3)如图③,过点C作CG⊥AD,交AD延长线于点G.∵AD∥BC,∴∠A=∠B=90°,又∠CGA=90°,AB=BC,∴四边形ABCG为正方形.∴AG=BC.已知∠DCE=45°,根据(1)(2)可知,ED=BE+DG.所以10=4+DG,即DG=6,AD=12-6=6,所以四边形ABCD的面积为S=(AD+BC)·AB=×(6+12)×12=108.答:四边形ABCD的面积为108
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
