2015(秋)北师大版九年级数学上册课时集训:12 矩形的性质与判定(共3份附答案)
文档属性
| 名称 | 2015(秋)北师大版九年级数学上册课时集训:12 矩形的性质与判定(共3份附答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 168.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-15 00:00:00 | ||
图片预览




文档简介
1.2 矩形的性质与判定
第1课时 矩形的性质
1.有一个角是__直角__的平行四边形叫做矩形.
2.矩形的四个角都是__直角__;矩形的对角线__相等__.
3.直角三角形斜边上的中线__等于斜边的一半__.
知识点一:矩形的性质
1.下列性质中,矩形具有但平行四边形不一定具有的是( C )
A.对边相等 B.对角相等
C.对角线相等 D.对边平行
2.矩形具有而菱形不具有的性质是( B )
A.两组对边分别平行 B.对角线相等
C.对角线互相平分 D.两组对角分别相等
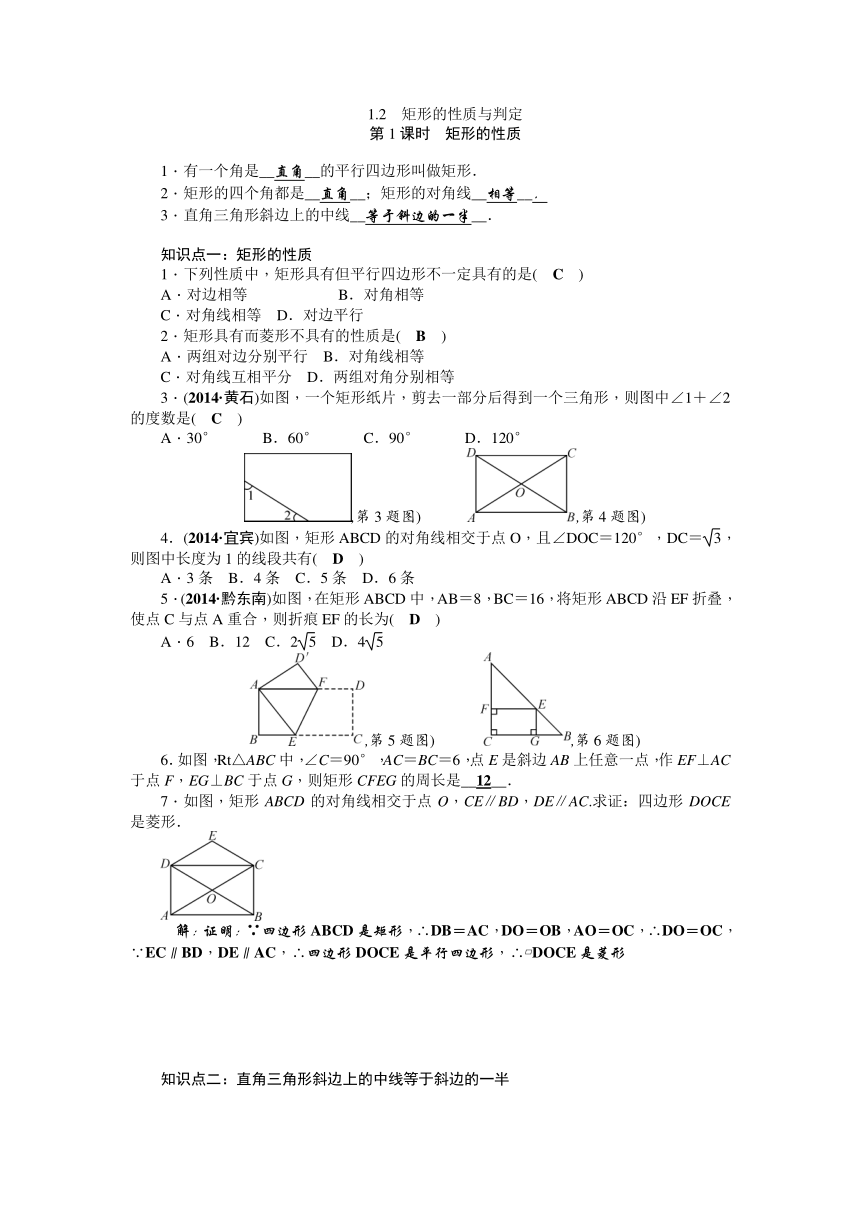
3.(2014·黄石)如图,一个矩形纸片,剪去一部分后得到一个三角形,则图中∠1+∠2的度数是( C )
A.30° B.60° C.90° D.120°
,第3题图) ,第4题图)
4.(2014·宜宾)如图,矩形ABCD的对角线相交于点O,且∠DOC=120°,DC=,则图中长度为1的线段共有( D )
A.3条 B.4条 C.5条 D.6条
5.(2014·黔东南)如图,在矩形AB ( http: / / www.21cnjy.com )CD中,AB=8,BC=16,将矩形ABCD沿EF折叠,使点C与点A重合,则折痕EF的长为( D )
A.6 B.12 C.2 D.4
,第5题图) ,第6题图)
6.如图,Rt△ABC中,∠C=90°,A ( http: / / www.21cnjy.com )C=BC=6,点E是斜边AB上任意一点,作EF⊥AC于点F,EG⊥BC于点G,则矩形CFEG的周长是__12__.
7.如图,矩形ABCD的对角线相交于点O,CE∥BD,DE∥AC.求证:四边形DOCE是菱形.
解:证明:∵四边形ABCD是矩形,∴DB ( http: / / www.21cnjy.com )=AC,DO=OB,AO=OC,∴DO=OC,∵EC∥BD,DE∥AC,∴四边形DOCE是平行四边形,∴ DOCE是菱形
知识点二:直角三角形斜边上的中线等于斜边的一半
8.(易错题)如图,在Rt ( http: / / www.21cnjy.com )△ABC中,∠ACB=90°,点D,E,F分别是AB,BC,CA的中点,若EF=4 cm,则CD=__4__cm.
9.如图,“人字形屋梁”中,AB=AC ( http: / / www.21cnjy.com ),点E,F,D分别是AB,AC,BC的中点,若AB=6 m,∠B=30°,则支撑人字形屋梁的木料DE,AD,DF共有__9__米.
10.直角三角形斜边上的高与中线分别是5 cm和6 cm,则它的面积是__30_cm2__.
11.如图,点O是矩形ABCD的对角线AC的中点,点M是AD的中点,若AB=5,AD=12,则四边形ABOM的周长为__20__.
12.如图,已知矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,若∠DAE∶∠BAE=3∶1,则∠EAC的度数是( C )
A.18° B.36° C.45° D.72°
,第12题图) ,第13题图)
13.(2014·青岛)如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上.若AB=6,BC=9,则BF的长为( A )
A.4 B.3 C.4.5 D.5
14.(2014·凉山)顺次连接矩形各边中点所形成的四边形是__菱形__.
15.如图所示,在△ABC中,BD ( http: / / www.21cnjy.com ),CE是高,点G,F分别是BC,DE的中点,则下列结论中:①GE=GD;②GF⊥DE;③GF平分∠DGE;④∠DGE=60°.其中正确的是__①②③__.(填写序号)
16.(2014·湘潭)如图,将矩形ABCD沿BD对折,点A落在点E处,BE与CD相交于点F,若AD=3,BD=6.
(1)求证:△EDF≌△CBF;
(2)求∠EBC的度数.
解:(1)证明:由折叠的性质可得 ( http: / / www.21cnjy.com ),DE=BC,∠E=∠C=90°,在△DEF和△BCF中∴△DEF≌△BCF(AAS) (2)在Rt△ABD中,∵AD=3,BD=6,∴∠ABD=30°,由折叠的性质可得;∠DBE=∠ABD=30°,∴∠EBC=90°-30°-30°=30°
17.如图所示,矩形ABCD的对角线AC,BD相交于点O,AE⊥BD,垂足为点E,∠1=∠2,OB=6 cm.
(1)求∠BOC的度数;
(2)求△DOC的周长.
解:(1)∵AE⊥BD, ∴∠AEO=∠A ( http: / / www.21cnjy.com )EB=90°,又∵AE=AE,∠1=∠2,∴△AEO≌△AEB.∴AB=AO.又∵OA=OB, ∴△AOB为等边三角形,∴∠AOB=60°,∴∠BOC=120° (2)由矩形的性质可得△OCD≌△OAB,∴OC=OA=OB=6 cm. ∴△DOC的周长为18 cm
18.(2014·邵阳)准备一张矩形纸片,按如图操作:
将△ABE沿BE翻折,使点A落在对角线BD上的M点,将△CDF沿DF翻折,使点C落在对角线BD上的N点.
(1)求证:四边形BFDE是平行四边形;
(2)若四边形BFDE是菱形,AB=2,求菱形BFDE的面积.
解:(1)证明:∵四边形 ( http: / / www.21cnjy.com )ABCD是矩形,∴∠A=∠C=90°,AB=CD,AB∥CD,∴∠ABD=∠CDB,∴∠EBD=∠FDB,∴EB∥DF,∵ED∥BF,∴四边形BFDE为平行四边形 (2)∵四边形BFDE为菱形,∴BE=ED,∠EBD=∠FBD=∠ABE,∵四边形ABCD是矩形,∴AD=BC,∠ABC=90°,∴∠ABE=30°,∵∠A=90°,AB=2,∴AE=,BF=BE=2AE=,∴菱形BFDE的面积为:×2=
第2课时 矩形的判定
对角线__相等__的平行四边形是矩形;有__三__个角是直角的四边形是矩形.
知识点一:对角线相等的平行四边形是矩形
1.四边形ABCD的对角线AC,BD相交于点O,下列各条件中,能判断四边形ABCD是矩形的是( B )
A.AO=CO,BO=DO
B.AO=BO=CO=DO
C.AC=BD,AO=CO
D.AO=CO,BO=DO,AC⊥BD
2.下列关于矩形的说法中正确的是( D )
A.对角线相等的四边形是矩形
B.对角线互相平分的四边形是矩形
C.矩形的对角线互相垂直平分
D.矩形的对角线相等且互相平分
3.如图,在 ABCD中,对角线AC,BD相交于点O,OA=2,若要使 ABCD为矩形,则OB的长应该为( C )
A.4 B.3 C.2 D.1
,第3题图) ,第4题图)
4.如图,要使平行四边形ABCD是矩形,则应添加的条件是__∠ABC=90°或AC=BD(不唯一)__.(添加一个条件即可)
5.(易错题)如图,在△ ( http: / / www.21cnjy.com )ABC中,AB=AC,将△ABC绕点C旋转180°得到△FEC,连接AE,BF.当∠ACB为__60__度时,四边形ABFE为矩形.
6.(原创题)已知,如图,在 ABCD ( http: / / www.21cnjy.com )中,对角线AC,BD相交于点O,且△OAB是等边三角形,若 ABCD的面积是16,求对角线AC的长.
解:∵△OAB是等边三角形,∴OA= ( http: / / www.21cnjy.com )OB,∠OAB=60°,又∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,∴AC=BD,∴ ABCD是矩形,∴∠ABC=90°,∵∠OAB=60°,∴∠ACB=30°,∴AC=2AB,BC=AB,∴AB·AB=16,∴AB=4,∴AC=8
知识点二:有三个角是直角的四边形是矩形
7.在数学活动课上,同学们判断一个四边形门框是否为矩形.下面是某学习小组4位同学拟定的方案,其中正确的是( C )
A.测量对角线是否互相平分
B.测量两组对边是否分别相等
C.测量其中三个角是否都为直角
D.测量对角线是否相等
8.如图,直角∠AOB内的一点P到这个角的两边的距离之和为6,则图中四边形的周长为__12__.
9.如图,点M是矩形ABCD的边A ( http: / / www.21cnjy.com )D的中点,点P为BC上一点,PE⊥MC于点E,PF⊥MB于点F,当AB,BC满足条件__BC=2AB__时,四边形PEMF为矩形.
10.已知 ABCD的对角线交于点O,分 ( http: / / www.21cnjy.com )别添加下列条件:①∠ABC=90°;②AC⊥BD;③AC=BD;④OA=OD.使 ABCD是矩形的条件的序号是__①③④__.
11.如图,点E,F分别△ABC的边BC,CA的中点,延长EF到点D,使得DF=EF,连接DA,DC,AE.
(1)求证:四边形ABED是平行四边形;
(2)若AB=AC,求证:四边形AECD是矩形.
解:(1)证明:∵AF=CF,DF ( http: / / www.21cnjy.com )=EF,∴四边形AECD是平行四边形,∴AD∥BC,AD=CE,又∵BE=CE,∴AD=BE,∴四边形ABED是平行四边形
(2)∵AB=AC,BE=CE,∴AE⊥BC,∴∠AEC=90°,∴ AECD是矩形
12.如图,四边形ABCD的对角线AC,BD交于点O,BE⊥AC于点E,DF⊥AC于点F,点O既是AC的中点,又是EF的中点.
(1)求证:△BOE≌△DOF;
(2)若OA=BD,则四边形ABCD是什么特殊四边形?请说明理由.
解:(1)证明:∵BE⊥AC,DF⊥ ( http: / / www.21cnjy.com )AC,∴∠BEO=∠DFO=90°,∵点O是EF的中点,∴OE=OF,又∵∠DOF=∠BOE,∴△BOE≌△DOF(ASA)
(2)四边形ABCD是矩形.理 ( http: / / www.21cnjy.com )由如下:∵△BOE≌△DOF,∴OB=OD,又∵OA=OC,∴四边形ABCD是平行四边形,∵OA=BD,OA=AC,∴BD=AC,∴ ABCD是矩形
13.如图,AB=AC,AD=AE,DE=BC且∠BAD=∠CAE,求证:四边形BCDE是矩形.
解:证明:∵AC=AB,AD=AE, ( http: / / www.21cnjy.com )∠BAD=∠CAE,∴∠CAD=∠BAD-∠CAB=∠CAE-∠CAB=∠BAE.∴△ADC≌△AEB.∴DC=BE,∠ABE=∠ACD.又∵DE=BC,∴四边形BCDE为平行四边形.∵AB=AC,∴∠ABC=ACB,∴∠ABC+∠ABE=∠ACB+∠ACD,即∠EBC=∠DCB=90°.∴四边形BCED为矩形
14.(教材例4变式题)如图,△ABC中, ( http: / / www.21cnjy.com )点O是边AC上一个动点,过点O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.连接AE,AF.
(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
解:(1)证明:∵CF平分 ( http: / / www.21cnjy.com )∠ACD,且MN∥BD,∴∠ACF=∠FCD=∠CFO.∴OF=OC.同理可证:OC=OE.∴OE=OF (2)由(1)知:OF=OC,OC=OE,∴∠OCF=∠OFC,∠OCE=∠OEC.∴∠OCF+∠OCE=∠OFC+∠OEC.而∠OCF+∠OCE+∠OFC+∠OEC=180°,∴∠ECF=∠OCF+∠OCE=90°,∴EF===13.∴OC=EF= (3)当点O在边AC上运动到AC中点时,四边形AECF是矩形..理由如下:由(1)知OE=OF, 当点O移动到AC中点时有OA=OC,∴四边形AECF是平行四边形, ∵∠ECF=90°, ∴平行四边形AECF是矩形
第3课时 矩形的性质与判定的综合运用
1.矩形的性质:(1)矩形具有__平行四边形__的一切性质;(2)矩形的四个角都是__直角__;(3)矩形的对角线__相等__.
2.矩形的判定:(1)有一个角是__直 ( http: / / www.21cnjy.com )角__的平行四边形是矩形;(2)有三个角是__直角__的__四边形__是矩形;(3)对角线__相等__的__平行四边形__是矩形.
知识点:矩形的性质与判定的综合运用
1.如图,四边形ABCD和四边形AEF ( http: / / www.21cnjy.com )C是两个矩形,点B在EF边上,若矩形ABCD和矩形AEFC的面积分别是S1,S2,则S1,S2的大小关系是( B )
A.S1>S2 B.S1=S2
C.S1,第1题图) ,第2题图)
2.如图,在△ABC中,点D,E,F分别是AB,AC,BC的中点,AH⊥BC于点H,连接EH,若DF=10 cm,则EH等于( B )
A.8 cm B.10 cm C.16 cm D.24 cm
3.如图,矩形OBCD的顶点C的坐标为(1,3),则对角线BD的长等于( D )
A. B.2
C.2 D.
4.在四边形ABCD中,AC和BD的交点为点O,下列条件中不能判定四边形ABCD是矩形的是( C )
A.AB=CD,AD=BC,AC=BD
B.AO=CO,BO=DO,∠A=90°
C.∠A=∠C,∠B+∠C=180°,∠AOB=∠BOC
D.AB∥CD,AB=CD,∠A=90°
5.如图,矩形ABCD的对角线相交于点O,AE平分∠BAD交BC于点E,若∠CAE=15°,则∠BOE=__75__度.
,第5题图) ,第6题图)
6.如图,在矩形ABCD中,AB=2,B ( http: / / www.21cnjy.com )C=4,点A,B分别在y轴,x轴的正半轴上,点C在第一象限,如果∠OAB=30°,那么点C的坐标为__(1+2,2)__.
7.平行四边形的四个内角平分线相交,如果能构成四边形,则这个四边形是__矩形__.
8.在四边形ABCD中,对角线AC,BD交于 ( http: / / www.21cnjy.com )点O,从①AB=CD;②AB∥CD;③OA=OC;④OB=OD;⑤AC=BD;⑥∠ABC=90°.这六个条件中,可选取三个推出四边形ABCD是矩形,如①②⑤ 四边形ABCD是矩形,请再写出符合要求的两个:__①②⑥ 四边形ABCD是矩形;③④⑤ 四边形ABCD是矩形;(另外③④⑥,②③⑤ 四边形ABCD是矩形)__.
9.如图,四边形ABCD是矩形,对角线AC,BD相交于点O,BE∥AC交DC的延长线于点E.
(1)求证:BD=BE;
(2)若∠DBC=30°,BO=4,求四边形ABED的面积.
解:(1)证明:∵四边形ABCD是 ( http: / / www.21cnjy.com )矩形,∴BD=AC,AB∥CE,又∵BE∥AC,∴四边形ABEC是平行四边形,∴BE=AC,∴BD=BE (2)S四边形ABED=(AB+DE)·BC=(4+8)×4=24
10.如图,在矩形ABCD中,AB=2,BC=4,对角线AC的垂直平分线分别交AD,AC于点E,O,连接CE,则CE的长为( C )
A.3 B.3.5
C.2.5 D.2.8
11.矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,若OE∶ED=1∶3,AE=,则BD=__4或__.
12.如图,在矩形ABCD中,两条对角线AC,BD相交于点O,点E是AC上的一点,且BO=2AE,∠AOD=120°,求证:BE⊥AC.
解:证明△AOB为等边三角形,点E是OA的中点即可
13.如图,矩形ABCD中,AC,BD相交于点O,点E为矩形ABCD外一点,若AE⊥CE,求证:BE⊥DE.
解:连接OE,∵四边形ABCD是矩形 ( http: / / www.21cnjy.com ),∴OA=OC,OB=OD,AC=BD,∵AE⊥CE,∴OE=AC,∴OE=BD,∴OE=OB=OD,可证∠BED=90°,∴BE⊥DE
14.如图,四边形ABCD是菱形,点E,F,G,H分别是AD,AB,BC,CD的中点.
(1)求证:四边形EFGH是矩形;
(2)若菱形ABCD的面积是50,求四边形EFGH的面积.
解:(1)∵点E,F分别是AD,AB的 ( http: / / www.21cnjy.com )中点,∴EF綊DB,同理GH綊DB,∴EF綊GH,∴四边形EFGH是平行四边形,又∵四边形ABCD是菱形,∴AC⊥BD,∴EF⊥AC,∴FG⊥EF,∴∠GFE=90°,∴四边形EFGH是矩形 (2)由(1)知EF=DB,FG=AC,∴S矩形EFGH=EF·FG=AC·BD=·(·AC·BD)=×50=25
15.如图,点D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC.
(1)求证:CD=AN;
(2)若∠AMD=2∠MCD,求证:四边形ADCN是矩形.
解:(1)证△AMD≌△CMN得 ( http: / / www.21cnjy.com )AD=CN,又∵AD∥CN,∴四边形ADCN是平行四边形,∴CD=AN (2)∵∠AMD=2∠MCD,∠AMD=∠MCD+∠MDC,∴∠MCD=∠MDC,∴MD=MC,由(1)知四边形ADCN是平行四边形,∴MD=MN=MA=MC,∴AC=DN,∴ ADCN是矩形
16.如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.
(1)求证:CM=CN;
(2)若△CMN的面积与△CDN的面积比为3∶1,求的值.
解:(1)∵四边形ABCD是矩形, ( http: / / www.21cnjy.com )∴AD∥BC,∴∠ANM=∠CMN,由折叠知∠CNM=∠ANM,∴∠CNM=∠CMN,∴CN=CM (2)∵AD∥BC,S△CMN∶S△CDN=3∶1,∴CM∶DN=3∶1,设DN=x,则CM=3x,过点N作NK⊥BC于点K,∵DC⊥BC,∴NK∥DC,又∵AD∥BC,∴CK=DN=x,MK=2x,由(1)知CN=CM=3x,∴NK2=CN2-CK2=(3x)2-x2=8x2,∴MN===2x,∴==2
第1课时 矩形的性质
1.有一个角是__直角__的平行四边形叫做矩形.
2.矩形的四个角都是__直角__;矩形的对角线__相等__.
3.直角三角形斜边上的中线__等于斜边的一半__.
知识点一:矩形的性质
1.下列性质中,矩形具有但平行四边形不一定具有的是( C )
A.对边相等 B.对角相等
C.对角线相等 D.对边平行
2.矩形具有而菱形不具有的性质是( B )
A.两组对边分别平行 B.对角线相等
C.对角线互相平分 D.两组对角分别相等
3.(2014·黄石)如图,一个矩形纸片,剪去一部分后得到一个三角形,则图中∠1+∠2的度数是( C )
A.30° B.60° C.90° D.120°
,第3题图) ,第4题图)
4.(2014·宜宾)如图,矩形ABCD的对角线相交于点O,且∠DOC=120°,DC=,则图中长度为1的线段共有( D )
A.3条 B.4条 C.5条 D.6条
5.(2014·黔东南)如图,在矩形AB ( http: / / www.21cnjy.com )CD中,AB=8,BC=16,将矩形ABCD沿EF折叠,使点C与点A重合,则折痕EF的长为( D )
A.6 B.12 C.2 D.4
,第5题图) ,第6题图)
6.如图,Rt△ABC中,∠C=90°,A ( http: / / www.21cnjy.com )C=BC=6,点E是斜边AB上任意一点,作EF⊥AC于点F,EG⊥BC于点G,则矩形CFEG的周长是__12__.
7.如图,矩形ABCD的对角线相交于点O,CE∥BD,DE∥AC.求证:四边形DOCE是菱形.
解:证明:∵四边形ABCD是矩形,∴DB ( http: / / www.21cnjy.com )=AC,DO=OB,AO=OC,∴DO=OC,∵EC∥BD,DE∥AC,∴四边形DOCE是平行四边形,∴ DOCE是菱形
知识点二:直角三角形斜边上的中线等于斜边的一半
8.(易错题)如图,在Rt ( http: / / www.21cnjy.com )△ABC中,∠ACB=90°,点D,E,F分别是AB,BC,CA的中点,若EF=4 cm,则CD=__4__cm.
9.如图,“人字形屋梁”中,AB=AC ( http: / / www.21cnjy.com ),点E,F,D分别是AB,AC,BC的中点,若AB=6 m,∠B=30°,则支撑人字形屋梁的木料DE,AD,DF共有__9__米.
10.直角三角形斜边上的高与中线分别是5 cm和6 cm,则它的面积是__30_cm2__.
11.如图,点O是矩形ABCD的对角线AC的中点,点M是AD的中点,若AB=5,AD=12,则四边形ABOM的周长为__20__.
12.如图,已知矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,若∠DAE∶∠BAE=3∶1,则∠EAC的度数是( C )
A.18° B.36° C.45° D.72°
,第12题图) ,第13题图)
13.(2014·青岛)如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上.若AB=6,BC=9,则BF的长为( A )
A.4 B.3 C.4.5 D.5
14.(2014·凉山)顺次连接矩形各边中点所形成的四边形是__菱形__.
15.如图所示,在△ABC中,BD ( http: / / www.21cnjy.com ),CE是高,点G,F分别是BC,DE的中点,则下列结论中:①GE=GD;②GF⊥DE;③GF平分∠DGE;④∠DGE=60°.其中正确的是__①②③__.(填写序号)
16.(2014·湘潭)如图,将矩形ABCD沿BD对折,点A落在点E处,BE与CD相交于点F,若AD=3,BD=6.
(1)求证:△EDF≌△CBF;
(2)求∠EBC的度数.
解:(1)证明:由折叠的性质可得 ( http: / / www.21cnjy.com ),DE=BC,∠E=∠C=90°,在△DEF和△BCF中∴△DEF≌△BCF(AAS) (2)在Rt△ABD中,∵AD=3,BD=6,∴∠ABD=30°,由折叠的性质可得;∠DBE=∠ABD=30°,∴∠EBC=90°-30°-30°=30°
17.如图所示,矩形ABCD的对角线AC,BD相交于点O,AE⊥BD,垂足为点E,∠1=∠2,OB=6 cm.
(1)求∠BOC的度数;
(2)求△DOC的周长.
解:(1)∵AE⊥BD, ∴∠AEO=∠A ( http: / / www.21cnjy.com )EB=90°,又∵AE=AE,∠1=∠2,∴△AEO≌△AEB.∴AB=AO.又∵OA=OB, ∴△AOB为等边三角形,∴∠AOB=60°,∴∠BOC=120° (2)由矩形的性质可得△OCD≌△OAB,∴OC=OA=OB=6 cm. ∴△DOC的周长为18 cm
18.(2014·邵阳)准备一张矩形纸片,按如图操作:
将△ABE沿BE翻折,使点A落在对角线BD上的M点,将△CDF沿DF翻折,使点C落在对角线BD上的N点.
(1)求证:四边形BFDE是平行四边形;
(2)若四边形BFDE是菱形,AB=2,求菱形BFDE的面积.
解:(1)证明:∵四边形 ( http: / / www.21cnjy.com )ABCD是矩形,∴∠A=∠C=90°,AB=CD,AB∥CD,∴∠ABD=∠CDB,∴∠EBD=∠FDB,∴EB∥DF,∵ED∥BF,∴四边形BFDE为平行四边形 (2)∵四边形BFDE为菱形,∴BE=ED,∠EBD=∠FBD=∠ABE,∵四边形ABCD是矩形,∴AD=BC,∠ABC=90°,∴∠ABE=30°,∵∠A=90°,AB=2,∴AE=,BF=BE=2AE=,∴菱形BFDE的面积为:×2=
第2课时 矩形的判定
对角线__相等__的平行四边形是矩形;有__三__个角是直角的四边形是矩形.
知识点一:对角线相等的平行四边形是矩形
1.四边形ABCD的对角线AC,BD相交于点O,下列各条件中,能判断四边形ABCD是矩形的是( B )
A.AO=CO,BO=DO
B.AO=BO=CO=DO
C.AC=BD,AO=CO
D.AO=CO,BO=DO,AC⊥BD
2.下列关于矩形的说法中正确的是( D )
A.对角线相等的四边形是矩形
B.对角线互相平分的四边形是矩形
C.矩形的对角线互相垂直平分
D.矩形的对角线相等且互相平分
3.如图,在 ABCD中,对角线AC,BD相交于点O,OA=2,若要使 ABCD为矩形,则OB的长应该为( C )
A.4 B.3 C.2 D.1
,第3题图) ,第4题图)
4.如图,要使平行四边形ABCD是矩形,则应添加的条件是__∠ABC=90°或AC=BD(不唯一)__.(添加一个条件即可)
5.(易错题)如图,在△ ( http: / / www.21cnjy.com )ABC中,AB=AC,将△ABC绕点C旋转180°得到△FEC,连接AE,BF.当∠ACB为__60__度时,四边形ABFE为矩形.
6.(原创题)已知,如图,在 ABCD ( http: / / www.21cnjy.com )中,对角线AC,BD相交于点O,且△OAB是等边三角形,若 ABCD的面积是16,求对角线AC的长.
解:∵△OAB是等边三角形,∴OA= ( http: / / www.21cnjy.com )OB,∠OAB=60°,又∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,∴AC=BD,∴ ABCD是矩形,∴∠ABC=90°,∵∠OAB=60°,∴∠ACB=30°,∴AC=2AB,BC=AB,∴AB·AB=16,∴AB=4,∴AC=8
知识点二:有三个角是直角的四边形是矩形
7.在数学活动课上,同学们判断一个四边形门框是否为矩形.下面是某学习小组4位同学拟定的方案,其中正确的是( C )
A.测量对角线是否互相平分
B.测量两组对边是否分别相等
C.测量其中三个角是否都为直角
D.测量对角线是否相等
8.如图,直角∠AOB内的一点P到这个角的两边的距离之和为6,则图中四边形的周长为__12__.
9.如图,点M是矩形ABCD的边A ( http: / / www.21cnjy.com )D的中点,点P为BC上一点,PE⊥MC于点E,PF⊥MB于点F,当AB,BC满足条件__BC=2AB__时,四边形PEMF为矩形.
10.已知 ABCD的对角线交于点O,分 ( http: / / www.21cnjy.com )别添加下列条件:①∠ABC=90°;②AC⊥BD;③AC=BD;④OA=OD.使 ABCD是矩形的条件的序号是__①③④__.
11.如图,点E,F分别△ABC的边BC,CA的中点,延长EF到点D,使得DF=EF,连接DA,DC,AE.
(1)求证:四边形ABED是平行四边形;
(2)若AB=AC,求证:四边形AECD是矩形.
解:(1)证明:∵AF=CF,DF ( http: / / www.21cnjy.com )=EF,∴四边形AECD是平行四边形,∴AD∥BC,AD=CE,又∵BE=CE,∴AD=BE,∴四边形ABED是平行四边形
(2)∵AB=AC,BE=CE,∴AE⊥BC,∴∠AEC=90°,∴ AECD是矩形
12.如图,四边形ABCD的对角线AC,BD交于点O,BE⊥AC于点E,DF⊥AC于点F,点O既是AC的中点,又是EF的中点.
(1)求证:△BOE≌△DOF;
(2)若OA=BD,则四边形ABCD是什么特殊四边形?请说明理由.
解:(1)证明:∵BE⊥AC,DF⊥ ( http: / / www.21cnjy.com )AC,∴∠BEO=∠DFO=90°,∵点O是EF的中点,∴OE=OF,又∵∠DOF=∠BOE,∴△BOE≌△DOF(ASA)
(2)四边形ABCD是矩形.理 ( http: / / www.21cnjy.com )由如下:∵△BOE≌△DOF,∴OB=OD,又∵OA=OC,∴四边形ABCD是平行四边形,∵OA=BD,OA=AC,∴BD=AC,∴ ABCD是矩形
13.如图,AB=AC,AD=AE,DE=BC且∠BAD=∠CAE,求证:四边形BCDE是矩形.
解:证明:∵AC=AB,AD=AE, ( http: / / www.21cnjy.com )∠BAD=∠CAE,∴∠CAD=∠BAD-∠CAB=∠CAE-∠CAB=∠BAE.∴△ADC≌△AEB.∴DC=BE,∠ABE=∠ACD.又∵DE=BC,∴四边形BCDE为平行四边形.∵AB=AC,∴∠ABC=ACB,∴∠ABC+∠ABE=∠ACB+∠ACD,即∠EBC=∠DCB=90°.∴四边形BCED为矩形
14.(教材例4变式题)如图,△ABC中, ( http: / / www.21cnjy.com )点O是边AC上一个动点,过点O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.连接AE,AF.
(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
解:(1)证明:∵CF平分 ( http: / / www.21cnjy.com )∠ACD,且MN∥BD,∴∠ACF=∠FCD=∠CFO.∴OF=OC.同理可证:OC=OE.∴OE=OF (2)由(1)知:OF=OC,OC=OE,∴∠OCF=∠OFC,∠OCE=∠OEC.∴∠OCF+∠OCE=∠OFC+∠OEC.而∠OCF+∠OCE+∠OFC+∠OEC=180°,∴∠ECF=∠OCF+∠OCE=90°,∴EF===13.∴OC=EF= (3)当点O在边AC上运动到AC中点时,四边形AECF是矩形..理由如下:由(1)知OE=OF, 当点O移动到AC中点时有OA=OC,∴四边形AECF是平行四边形, ∵∠ECF=90°, ∴平行四边形AECF是矩形
第3课时 矩形的性质与判定的综合运用
1.矩形的性质:(1)矩形具有__平行四边形__的一切性质;(2)矩形的四个角都是__直角__;(3)矩形的对角线__相等__.
2.矩形的判定:(1)有一个角是__直 ( http: / / www.21cnjy.com )角__的平行四边形是矩形;(2)有三个角是__直角__的__四边形__是矩形;(3)对角线__相等__的__平行四边形__是矩形.
知识点:矩形的性质与判定的综合运用
1.如图,四边形ABCD和四边形AEF ( http: / / www.21cnjy.com )C是两个矩形,点B在EF边上,若矩形ABCD和矩形AEFC的面积分别是S1,S2,则S1,S2的大小关系是( B )
A.S1>S2 B.S1=S2
C.S1
2.如图,在△ABC中,点D,E,F分别是AB,AC,BC的中点,AH⊥BC于点H,连接EH,若DF=10 cm,则EH等于( B )
A.8 cm B.10 cm C.16 cm D.24 cm
3.如图,矩形OBCD的顶点C的坐标为(1,3),则对角线BD的长等于( D )
A. B.2
C.2 D.
4.在四边形ABCD中,AC和BD的交点为点O,下列条件中不能判定四边形ABCD是矩形的是( C )
A.AB=CD,AD=BC,AC=BD
B.AO=CO,BO=DO,∠A=90°
C.∠A=∠C,∠B+∠C=180°,∠AOB=∠BOC
D.AB∥CD,AB=CD,∠A=90°
5.如图,矩形ABCD的对角线相交于点O,AE平分∠BAD交BC于点E,若∠CAE=15°,则∠BOE=__75__度.
,第5题图) ,第6题图)
6.如图,在矩形ABCD中,AB=2,B ( http: / / www.21cnjy.com )C=4,点A,B分别在y轴,x轴的正半轴上,点C在第一象限,如果∠OAB=30°,那么点C的坐标为__(1+2,2)__.
7.平行四边形的四个内角平分线相交,如果能构成四边形,则这个四边形是__矩形__.
8.在四边形ABCD中,对角线AC,BD交于 ( http: / / www.21cnjy.com )点O,从①AB=CD;②AB∥CD;③OA=OC;④OB=OD;⑤AC=BD;⑥∠ABC=90°.这六个条件中,可选取三个推出四边形ABCD是矩形,如①②⑤ 四边形ABCD是矩形,请再写出符合要求的两个:__①②⑥ 四边形ABCD是矩形;③④⑤ 四边形ABCD是矩形;(另外③④⑥,②③⑤ 四边形ABCD是矩形)__.
9.如图,四边形ABCD是矩形,对角线AC,BD相交于点O,BE∥AC交DC的延长线于点E.
(1)求证:BD=BE;
(2)若∠DBC=30°,BO=4,求四边形ABED的面积.
解:(1)证明:∵四边形ABCD是 ( http: / / www.21cnjy.com )矩形,∴BD=AC,AB∥CE,又∵BE∥AC,∴四边形ABEC是平行四边形,∴BE=AC,∴BD=BE (2)S四边形ABED=(AB+DE)·BC=(4+8)×4=24
10.如图,在矩形ABCD中,AB=2,BC=4,对角线AC的垂直平分线分别交AD,AC于点E,O,连接CE,则CE的长为( C )
A.3 B.3.5
C.2.5 D.2.8
11.矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,若OE∶ED=1∶3,AE=,则BD=__4或__.
12.如图,在矩形ABCD中,两条对角线AC,BD相交于点O,点E是AC上的一点,且BO=2AE,∠AOD=120°,求证:BE⊥AC.
解:证明△AOB为等边三角形,点E是OA的中点即可
13.如图,矩形ABCD中,AC,BD相交于点O,点E为矩形ABCD外一点,若AE⊥CE,求证:BE⊥DE.
解:连接OE,∵四边形ABCD是矩形 ( http: / / www.21cnjy.com ),∴OA=OC,OB=OD,AC=BD,∵AE⊥CE,∴OE=AC,∴OE=BD,∴OE=OB=OD,可证∠BED=90°,∴BE⊥DE
14.如图,四边形ABCD是菱形,点E,F,G,H分别是AD,AB,BC,CD的中点.
(1)求证:四边形EFGH是矩形;
(2)若菱形ABCD的面积是50,求四边形EFGH的面积.
解:(1)∵点E,F分别是AD,AB的 ( http: / / www.21cnjy.com )中点,∴EF綊DB,同理GH綊DB,∴EF綊GH,∴四边形EFGH是平行四边形,又∵四边形ABCD是菱形,∴AC⊥BD,∴EF⊥AC,∴FG⊥EF,∴∠GFE=90°,∴四边形EFGH是矩形 (2)由(1)知EF=DB,FG=AC,∴S矩形EFGH=EF·FG=AC·BD=·(·AC·BD)=×50=25
15.如图,点D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC.
(1)求证:CD=AN;
(2)若∠AMD=2∠MCD,求证:四边形ADCN是矩形.
解:(1)证△AMD≌△CMN得 ( http: / / www.21cnjy.com )AD=CN,又∵AD∥CN,∴四边形ADCN是平行四边形,∴CD=AN (2)∵∠AMD=2∠MCD,∠AMD=∠MCD+∠MDC,∴∠MCD=∠MDC,∴MD=MC,由(1)知四边形ADCN是平行四边形,∴MD=MN=MA=MC,∴AC=DN,∴ ADCN是矩形
16.如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.
(1)求证:CM=CN;
(2)若△CMN的面积与△CDN的面积比为3∶1,求的值.
解:(1)∵四边形ABCD是矩形, ( http: / / www.21cnjy.com )∴AD∥BC,∴∠ANM=∠CMN,由折叠知∠CNM=∠ANM,∴∠CNM=∠CMN,∴CN=CM (2)∵AD∥BC,S△CMN∶S△CDN=3∶1,∴CM∶DN=3∶1,设DN=x,则CM=3x,过点N作NK⊥BC于点K,∵DC⊥BC,∴NK∥DC,又∵AD∥BC,∴CK=DN=x,MK=2x,由(1)知CN=CM=3x,∴NK2=CN2-CK2=(3x)2-x2=8x2,∴MN===2x,∴==2
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
