2015(秋)华师大版九年级数学上册课时集训:解直角三角形
文档属性
| 名称 | 2015(秋)华师大版九年级数学上册课时集训:解直角三角形 |  | |
| 格式 | zip | ||
| 文件大小 | 522.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-16 22:20:40 | ||
图片预览




文档简介
24.4 解直角三角形
第1课时 解直角三角形及其简单应用
1.在直角三角形中,由__已知__元素求出__未知__元素的过程,叫做解直角三角形.
2.在直角三角形中,除直角外还有__五__个元素,知道__两__个元素(至少有一个是边),就可以求出另外__三__个元素.
3.解直角三角形,一般是下面两种情况:(1)已知两条边;(2)已知一条边和一个__锐角__.
知识点1:已知两边解直角三角形
1.在△ABC中,∠C=90°,AC=4,AB=7,欲求∠A的值,最适宜的做法是( C )
A.计算tanA的值求出
B.计算sinA的值求出
C.计算cosA的值求出
D.先根据sinB求出∠B,再利用90°-∠B求出
2.在Rt△ABC中,∠C=90°,a=20,c=20,则∠A=__45°__,∠B=__45°__,b=__20__.
3.如图,在Rt△ABC中,∠C=90°,已知BC=3,AC=9,解此直角三角形.
解:AB=6 ∠A=30° ∠B=60°
知识点2:已知一边一锐角解直角三角形
4.在Rt△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C的对边,下列各式错误的是( B )
A.a=csinA B.b=ccosB
C.b=atanB D.a=btanA
5.(2014·杭州)在Rt△ABC中,已知∠C=90°,∠A=40°,BC=3,则AC=( D )
A.3sin40° B.3sin50°
C.3tan40° D.3tan50°
6.(2014·来宾)如图,Rt△ABC中,∠C=90°,∠B=30°,BC=6,则AB的长为__4__.
7.在Rt△ABC中,CA=CB,AB=9,点D在BC边上,连接AD,若tan∠CAD=,则BD的长为__6__.
8.在Rt△ABC中,∠C=90°,c=8,∠A=60°,解这个直角三角形.
解:∵∠A=60°,∴∠B=90°-∠A ( http: / / www.21cnjy.com )=30°.∵sinA=,∴a=c·sinA=8×sin60°=8×=12,∴b===4
知识点3:解直角三角形的简单应用
9.如图,为了测量河两岸A,B两点的距离,在与AB垂直的方向上取点C,测得AC=m,∠ACB=α,那么AB等于( C )
A.msinα B.mcosα
C.mtanα D.
10.如图,△ABC中,∠C=90°,点D在AC上,已知∠BDC=45°,BD=10,AB=20.求∠A的度数.
解:在Rt△BDC中,∵sin∠BDC=,∴BC=BD×sin∠BDC=10×sin45°=10.在Rt△ABC中,∵sin∠A===,∴∠A=30°
11.(2014·湖州)如图,已知Rt△ABC中,∠C=90°,AC=4,tanA=,则BC的长是( A )
A.2 B.8 C.2 D.4
,第11题图) ,第12题图)
12.(2014·扬州)如图,已知∠AOB ( http: / / www.21cnjy.com )=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=( C )
A.3 B.4 C.5 D.6
13.如图,在菱形ABCD中,DE⊥AB于点E,cosA=,BE=4,则tan∠DBE的值是__2__.
,第13题图) ,第14题图)
14.如图,已知在Rt△ABC中,斜边BC上的高AD=4,cosB=,则AC=__5__.
15.根据下列条件解Rt△ABC.(∠C=90°)
(1)∠A=30°,b=;
解:∠B=90°-∠A=90°-30°=60°,∵tanA=,∴a=b·tanA=×=1,∴c=2a=2
(2)c=4,b=2.
解:由勾股定理得:a===2.∵b=2,a=2,∠C=90°,∴∠A=∠B=45°
16.(2014·济宁)如图,在△ABC中,∠A=30°,∠B=45°,AC=2,求AB的长.
解:过点C作CD⊥AB于点 ( http: / / www.21cnjy.com )D,则∠ADC=∠BDC=90°.∵∠B=45°,∴∠BCD=∠B=45°,∴CD=BD.∵∠A=30°,AC=2,∴CD=,∴BD=CD=,由勾股定理得:AD==3,∴AB=AD+BD=3+
17.一个长方体木箱沿斜面下滑,当木箱 ( http: / / www.21cnjy.com )滑至如图位置时,AB=3 m.已知木箱高BE= m,斜面坡角为30°,求木箱端点E距地面AC的高度EF.
解:连接AE,在Rt△ABE中,A ( http: / / www.21cnjy.com )B=3 m,BE= m,则AE==2 m,又∵tan∠EAB==,∴∠EAB=30°,在Rt△AEF中,∠EAF=∠EAB+∠BAC=60°,∴EF=AE×sin∠EAF=2×sin60°=2×=3 m
18.探究:如图①,在△ABC中,∠A=α(0°<α<90°),AB=c,AC=b,试用含b,c,α的式子表示△ABC的面积;
应用:如图②,在 ABCD中,对角线AC,BD相交成的锐角为α,若AC=a,BD=b,试用含b,c,α的式子表示 ABCD的面积.
解:探究:过点B作BD⊥AC,垂足 ( http: / / www.21cnjy.com )为D.∵AB=c,∠A=α,∴BD=c·sinα,∴S△ABC=AC·BD=bcsinα.应用:过点C作CE⊥DO于点E.∴sinα=.∵在 ABCD中,AC=a,BD=b,∴CO=a,DO=b,∴S△COD=CO·DO·sinα=absinα,∴S△BCD=CE×BD=×asinα×b=absinα
第2课时 仰角、俯角与解直角三角形的应用
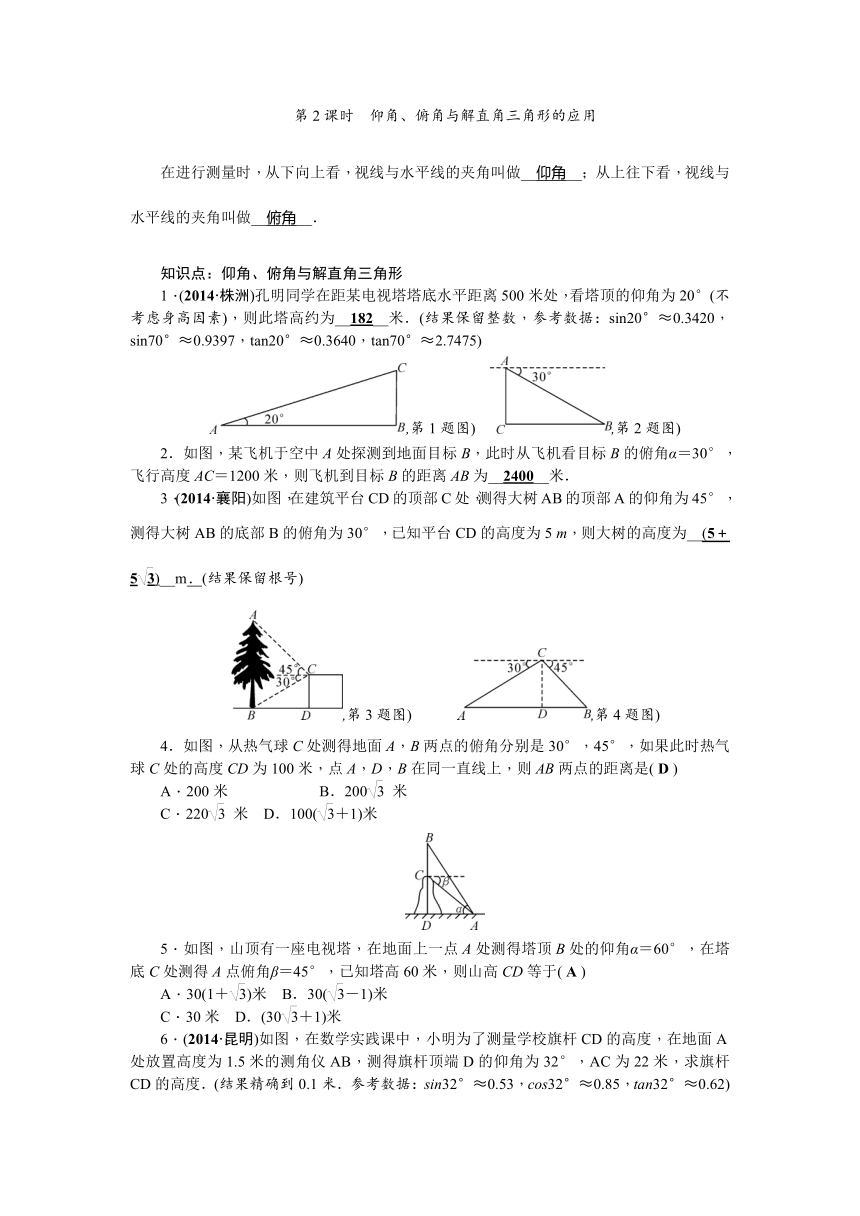
在进行测量时,从下向上看,视线与水平线的夹角叫做__仰角__;从上往下看,视线与水平线的夹角叫做__俯角__.
知识点:仰角、俯角与解直角三角形
1.(2014·株洲)孔明同学在距某电视塔塔 ( http: / / www.21cnjy.com )底水平距离500米处,看塔顶的仰角为20°(不考虑身高因素),则此塔高约为__182__米.(结果保留整数,参考数据:sin20°≈0.3420,sin70°≈0.9397,tan20°≈0.3640,tan70°≈2.7475)
,第1题图) ,第2题图)
2.如图,某飞机于空中A处 ( http: / / www.21cnjy.com )探测到地面目标B,此时从飞机看目标B的俯角α=30°,飞行高度AC=1200米,则飞机到目标B的距离AB为__2400__米.
3.(2014·襄阳)如 ( http: / / www.21cnjy.com )图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为5 m,则大树的高度为__(5+5)__m.(结果保留根号)
,第3题图) ,第4题图)
4.如图,从热气球C处测得地面A,B两 ( http: / / www.21cnjy.com )点的俯角分别是30°,45°,如果此时热气球C处的高度CD为100米,点A,D,B在同一直线上,则AB两点的距离是( D )
A.200米 B.200 米
C.220 米 D.100(+1)米
5.如图,山顶有一座电视塔,在地面上一 ( http: / / www.21cnjy.com )点A处测得塔顶B处的仰角α=60°,在塔底C处测得A点俯角β=45°,已知塔高60米,则山高CD等于( A )
A.30(1+)米 B.30(-1)米
C.30米 D.(30+1)米
6.(2014·昆明)如图,在数学 ( http: / / www.21cnjy.com )实践课中,小明为了测量学校旗杆CD的高度,在地面A处放置高度为1.5米的测角仪AB,测得旗杆顶端D的仰角为32°,AC为22米,求旗杆CD的高度.(结果精确到0.1米.参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)
解:过点B作BE⊥CD,垂足为E,在Rt ( http: / / www.21cnjy.com )△DEB中,∠DEB=90°,BE=AC=22(米),tan32°=,∴DE=BE·tan32°≈22×0.62=13.64(米).∵EC=AB=1.5,∴CD=CE+ED=1.5+13.64=15.14≈15.1(米).答:旗杆CD的高度为15.1米
7.(2014·广州)如图,某数学兴 ( http: / / www.21cnjy.com )趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10 m,到达B点,在B处测得树顶C的仰角高度为60°(A,B,D三点在同一直线上).请你根据他们测量数据计算这棵树CD的高度.(结果精确到0.1 m,参考数据:≈1.414,≈1.732)
解:∵∠CBD=∠A+∠ACB,∴∠A ( http: / / www.21cnjy.com )CB=∠CBD-∠A=60°-30°=30°,∴∠A=∠ACB,∴BC=AB=10(米).在直角△BCD中,CD=BC·sin∠CBD=10×=5≈5×1.732=8.7(米).答:这棵树CD的高度为8.7米
8.如图,小敏同学想测量一棵大 ( http: / / www.21cnjy.com )树的高度.她站在B处仰望树顶,测得仰角为30°,再往大树的方向前进4 m,测得仰角为60°,已知小敏同学身高(AB)为1.6 m,则这棵树的高度为( D )(结果精确到0.1 m,≈1.73)
A.3.5 m B.3.6 m
C.4.3 m D.5.1 m
9.(2014·自贡)如图,某学校新建 ( http: / / www.21cnjy.com )了一座吴玉章塑像,小林站在距离塑像2.7米的A处自B点看塑像头顶D的仰角为45°,看塑像底部C的仰角为30°,求塑像CD的高度.(结果精确到0.1米,参考数据:≈1.7)
解:在Rt△DEB中,DE=BE·tan4 ( http: / / www.21cnjy.com )5°=2.7米,在Rt△CEB中,CE=BE·tan30°=0.9米,则CD=DE-CE=2.7-0.9≈1.2米.故塑像CD的高度大约为1.2米
10.(2014·海南)如图 ( http: / / www.21cnjy.com ),一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行1 464米到B点处测得正前方C点处的俯角为45°.求海底C点处距离海面DF的深度.(结果精确到个位,参考数据:≈1.414,≈1.732,≈2.236)
解:作CE⊥AB于点E,依题意,AB= ( http: / / www.21cnjy.com )1 464,∠EAC=30°,∠CBE=45°,设CE=x,则BE=x,Rt△ACE中,tan30°===,整理得出:3x=1 464+x,解得x=732(+1)≈2 000米,∴x+600=2 600米.答:海底C点处距离DF的深度约为2 600米
11.(2014·哈尔滨)如图,AB, ( http: / / www.21cnjy.com )CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶部A点测建筑物CD的顶部C点的俯角∠EAC为30°.测得建筑物CD的底部D点的俯角∠EAD为45°.
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度.(结果保留根号)
解:(1)根据题意得,BD∥AE,∴∠A ( http: / / www.21cnjy.com )DB=∠EAD=45°,∵∠ABD=90°,∴∠BAD=∠ADB=45°,∴BD=AB=60,∴两建筑底部之间水平距离BD的长度为60米 (2)延长AE,DC交于点F,根据题意得四边形ABDF为正方形,∴AF=BD=DF=60,在Rt△AFC中,∠FAC=30°,∴CF=AF·tan∠FAC=60×=20,又∵FD=60,∴CD=60-20,∴建筑物CD的高度为(60-20)米
12.(2014·黔东南州)黔东南州某校九年 ( http: / / www.21cnjy.com )级某班开展数学活动,小明和小军合作用一副三角板测量学校的旗杆,小明站在B点测得旗杆顶端E点的仰角为45°,小军站在点D测得旗杆顶端E点的仰角为30°,已知小明和小军相距(BD)6米,小明的身高(AB)1.5米,小军的身高(CD)1.75米,求旗杆的高EF的长.(结果精确到0.1,参考数据:≈1.41,≈1.73)
解:过点A作AM⊥EF于点M,过点C ( http: / / www.21cnjy.com )作CN⊥EF于点N,∴MN=0.25米,∵∠EAM=45°,∴AM=ME,设AM=ME=x米,则CE=(x+6)米,EN=(x-0.25)米,∵∠ECN=30°,∴tan∠ECN===,解得x≈8.8,则EF=EN+MF≈8.8+1.5=10.3(米).答:旗杆的高EF为10.3米
第3课时 坡度与解直角三角形的应用
坡面的铅垂高度(h)和水平长度(l)的 ( http: / / www.21cnjy.com )比叫做坡面的__坡度__(或坡比),记作i,即i=____.坡度一般写成1∶m的形式.坡面与水平面的夹角叫做__坡角__,记作α,有i==__tanα__,坡度越大,坡角α就__越大__,坡面就__越陡__.
知识点1:坡度和坡角
1.(2014·怀化)如图,小明爬一土坡 ( http: / / www.21cnjy.com ),他从A处爬到B处所走的直线距离AB=4米,此时,他离地面高度为h=2米,则这个土坡的坡角∠A=__30°__.
2.某水库大坝的横断面是梯形,坝内斜坡的坡度i=1∶,坝外斜坡的坡度i=1∶1,则两个坡角的和为__75°__.
3.某人沿着有一定坡度的坡面前进了10米,此时他与水平地面的垂直距离为2 米,则这个坡面的坡度为__1∶2__.
知识点2:解有关坡度、坡角的实际问题
4.(2014·丽水)如图,河坝横 ( http: / / www.21cnjy.com )断面迎水坡AB的坡比是1∶(坡比是坡面的铅直高度BC与水平宽度AC之比),坝高BC=3 cm,则坡面AB的长度是( B )
A.9 m B.6 m C.6 m D.3 m
,第4题图) ,第5题图)
5.如图,先锋村准备在坡角为α的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为( B )
A.5cosα B.
C.5sinα D.
6.如图,斜坡AC的坡度(坡比)为1 ( http: / / www.21cnjy.com )∶,AC=10米.坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带AB相连,AB=14米.则旗杆BC的高度是__6__米.
7.(2014·巴中)如图,一水库大坝 ( http: / / www.21cnjy.com )的横断面为梯形ABCD,坝顶BC宽6米,坝高20米,斜坡AB的坡度i=1∶2.5,斜坡CD的坡角为30°,求坝底AD的长度.(精确到0.1米,参考数据:≈1.414,≈1.732.提示:坡度等于坡面的铅垂高度与水平长度之比)
解:作BE⊥AD,CF⊥AD ( http: / / www.21cnjy.com ),垂足分别为点E,F,则四边形BCFE是矩形,由题意得,BC=EF=6米,BE=CF=20米,斜坡AB的坡度i为1∶2.5,在Rt△ABE中,BE=20米,=,∴AE=50米.在Rt△CFD中,∠D=30°,∴DF=CF·cotD=20 米,∴AD=AE+EF+FD=50+6+20≈90.6(米).故坝底AD的长度约为90.6米
8.某商场为方便顾客使用购 ( http: / / www.21cnjy.com )物车,准备将滚动电梯的坡面坡度由1∶1.8改为1∶2.4(如图).如果改动后电梯的坡面长为13米,求改动后电梯水平宽度增加部分BC的长.
解:在Rt△ADC中,∵AD∶DC=1∶2 ( http: / / www.21cnjy.com ).4,AC=13,由AD2+DC2=AC2,得AD2+(2.4·AD)2=132,∴AD=5,∴DC=12米.在Rt△ABD中,∵AD∶BD=1∶1.8,∴BD=1.8·AD=9米,∴BC=DC-BD=12-9=3(米).答:改动后电梯水平宽度增加部分BC的长为3米
9.(2014·德州)如图是拦水坝的横断面,斜坡AB的水平宽度为12米,斜面坡度为1∶2,则是斜坡AB的长为( B )
A.4 米 B.6 米
C.12 米 D.24米
,第9题图) ,第10题图)
10.(2014·上海)如图,已知传送带与水 ( http: / / www.21cnjy.com )平面所成斜坡的坡度i=1∶2.4,如果它把物体送到离地面10米高的地方,那么物体所经过的路程为__26__米.
11.如图,某公园入口处原有三级台阶,每级台 ( http: / / www.21cnjy.com )阶高为18 cm,深为30 cm,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1∶5,则AC的长度是__210__cm.
12.某校教学楼后面紧邻着一 ( http: / / www.21cnjy.com )个山坡,坡上面是一块平地,如图所示,BC∥AD,BE⊥AD,斜坡AB长为 米,坡度i=9∶5.为了减缓坡面防止山体滑坡,保障安全,学校决定对该斜坡进行改造,地质人员勘测,当坡角不超过45°时,可确保山体不滑坡.
(1)求改造前坡顶到地面的距离BE的长;
(2)如果改造时保持坡脚A不动,坡顶B沿BC削进到F处,问BF至少是多少米?
解:(1)∵i==,设BE=9k,AE=5k(k为正数),则在Rt△AEB中,∠BEA=90°,AB=米,AB2=BE2+AE2,即()2=(9k)2+(5k)2,解得k=,∴BE=9×=22.5(米)(2)由(1)得AE=12.5,设BF=x,作FH⊥AD于点H,则=tan∠FAH,由题意得≤tan45°,即x≥10.所以坡顶B沿BC至少削进10米,才能确保安全
13.(2014·遵义)如图,一楼房AB后 ( http: / / www.21cnjy.com )有一假山,其坡度为i=1∶,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅垂高度与水平宽度的比)
解:过点E作EF⊥BC的延长线于点F, ( http: / / www.21cnjy.com )EH⊥AB于点H,在Rt△CEF中,∵i===tan∠ECF,∴∠ECF=30°,∴EF=CE=10米,CF=10米,∴BH=EF=10米,HE=BF=BC+CF=(25+10)米,在Rt△AHE中,∵∠HAE=45°,∴AH=HE=(25+10)米,∴AB=AH+HB=(35+10)米.答:楼房AB的高为(35+10)米
14.如图,某防洪指挥部发现长江边 ( http: / / www.21cnjy.com )一处长600米,高10米,背水坡的坡角为45°的防洪大堤(横断面为梯形ABCD)急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:背水坡面用土石进行加固,并使上底加宽3米,加固后背水坡EF的坡比i=1∶.
(1)求加固后坝底增加的宽度AF;(结果保留根号)
(2)求完成这项工程需要土石多少立方米?(结果保留根号)
解:(1)过点E,D作EM⊥BF ( http: / / www.21cnjy.com )于点M,DN⊥BF于点N,则MN=DE=2米,EM=DN=10米.在Rt△AND中,AN==10米.∵i==,∴FM=10米,∴AF=FM+MN-AN=(10-8)米 (2)∵S梯形ADEF==50-30,∴(50-30)×600≈(30000-18000)立方米.答:完成这项工程需要土石约(30000-18000)立方米
综合练习 解直角三角形的实际应用
1.如图为测量某物体AB的高度,在D点 ( http: / / www.21cnjy.com )测得A点的仰角为30°,朝物体AB方向前进20米到达点C,再次测得A点的仰角为60°,则物体的高度为( A )
A.10 米 B.10米 C.20 米 D. 米
,第1题图) ,第2题图)
2.(2014·临沂)如图,在某监 ( http: / / www.21cnjy.com )测点B处望见一艘正在作业的渔船在南偏西15°方向的A处,若渔船沿北偏西方75°方向以40海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B,C之间的距离为( C )
A.20海里 B.10 海里
C.20 海里 D.30海里
3.(2014·衡阳)如图,一河坝的 ( http: / / www.21cnjy.com )横断面为等腰梯形ABCD,坝顶宽10米,坝宽12米,斜坡AB的坡度i=1∶1.5,则坝底AD的长度为( D )
A.26米 B.28米 C.30米 D.46米
,第3题图) ,第4题图)
4.(2014·舟山)如图,在地面上的点A处测得树顶B的仰角为α度,AC=7米,则树高BC为__7tanα__米.(用含α的代数式表示)
5.如图,两建筑物的水平距离BC为18 ( http: / / www.21cnjy.com ) m,从A点测得D点的俯角α为30°,测得C点的俯角β为60°,则建筑物CD的高度为__12__m.(结果不作近似计算)
,第5题图) ,第6题图)
6.(2014·十堰)如 ( http: / / www.21cnjy.com )图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是__24__海里.(结果精确到个位,参考数据:≈1.4,≈1.7,≈2.4)
7.(2014·南京)如图,梯子斜 ( http: / / www.21cnjy.com )靠在与地面垂直(垂足为O)的墙上,当梯子位于AB位置时,它与地面所成的角∠ABO=60°;当梯子底端向右滑动1 m(即BD=1 m)到达CD的位置时,它与地面所成的角∠CDO=51°18′,求梯子的长.(参考数据:sin51°18′≈0.780,cos51°18′≈0.625,tan51°18′≈1.248)
解:设梯子的长x m.在 ( http: / / www.21cnjy.com )Rt△AOB中,cos∠ABO=,∴OB=AB·cos∠ABO=x·cos60°=x.在Rt△CDO中,cos∠CDO=,∴OD=CD·cos∠CDO=x·cos51°18′≈0.625x.∵BD=OD-OB,∴0.625x-x=1,解得x=8.故梯子的长是8米
8.(2014·烟台)小明坐于堤边 ( http: / / www.21cnjy.com )垂钓,如图,河堤AC的坡角为30°,AC的长米,钓竿AO的倾斜角是60°,其长为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离.
解:延长OA交BC于点D.∵AO ( http: / / www.21cnjy.com )的倾斜角是60°,∴∠ODB=60°.∵∠ACD=30°,∴∠CAD=180°-∠ODB-∠ODB-∠ACD=90°,在Rt△ACD中,AD=AC·tan∠ACD=·=(米),∴CD=2AD=3(米),又∵∠O=60°,∴△BOD是等边三角形,∴BD=OD=OA+AD=3+1.5=4.5(米),∴BC=BD-CD=4.5-3=1.5(米).答:浮漂B与河堤下端C之间的距离为1.5米
9.(2014·河南)在中俄“海上 ( http: / / www.21cnjy.com )联合-2014”反潜演习中,我军舰A测得潜艇C的俯角为30°.位于军舰A正上方1 000米的反潜直升机B测得潜艇C的俯角为68°.试根据以上数据求出潜艇C离开海平面的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5,≈1.7)
解:过点C作CD⊥BA的延 ( http: / / www.21cnjy.com )长线于点D.则AD即为潜艇C的下潜深度,根据题意得∠ACD=30°,∠BCD=68°.设AD=x,则BD=BA+AD=1 000+x.在Rt△ACD中,CD===x.在Rt△BCD中,BD=CD·tan68°.∴1 000+x=x·tan68°,∴x=≈≈308.∴潜艇C离开海平面的下潜深度约为308米
10.(2014·南充)马航M ( http: / / www.21cnjy.com )H370失联后,我国政府积极参与搜救.某日,我两艘专业救助船A,B同时收到有关可疑漂浮物的讯息,可疑漂浮物P在救助船A的北偏东53.5°方向上,在救助船B的西北方向上,船B在船A正东方向140海里处.(参考数据:sin36.5°≈0.6,cos36.5°≈0.8,tan36.5°≈0.75)
(1)求可疑漂浮物P到A,B两船所在直线的距离;
(2)若救助船A、救助船B分别以40海里/时,30海里/时的速度同时出发,匀速直线前往搜救,试通过计算判断哪艘船先到达P处.
解:(1)过点P作PH⊥AB于点E,由题意得 ( http: / / www.21cnjy.com ),∠PAE=36.5°,∠PBA=45°,在Rt△PAE中,=tan∠PAE=,即=0.75,解得x=60海里,∴可疑漂浮物P到A,B两船所在直线的距离为60海里 (2)在Rt△PBE中,PE=60海里,∠PBE=45°,则BP=PE=60≈84.8海里,B船需要的时间为:≈2.83小时,在Rt△PAE中,=sin∠PAE,∴AP=PE÷sin∠PAE=60÷0.6=100海里,∴A船需要的时间为:100÷40=2.5,∵2.83>2.5,∴A船先到达
11.(2014·安徽)如图,在同一 ( http: / / www.21cnjy.com )平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20 km;BC段与AB,CD段都垂直,长为10 km,CD段长为30 km,求两高速公路间的距离.(结果保留根号)
解:过B点作BE⊥l1, ( http: / / www.21cnjy.com )交l1于点E,CD于点F,l2于点G.在Rt△ABE中,BE=AB·sin30°=20×=10 km,在Rt△BCF中,BF=BC÷cos30°=10÷=km,CF=BF·sin30°=×=km,DF=CD-CF=(30-)km,在Rt△DFG中,FG=DF·sin30°=(30-)×=(15-)km,∴EG=BE+BF+FG=(25+5)km.故两高速公路间的距离为(25+5)km
12.
(2014·泸州)海中两 ( http: / / www.21cnjy.com )个灯塔A,B,其中B位于A的正东方向上,渔船跟踪鱼群由西向东航行,在点C处测得灯塔A在西北方向上,灯塔B在北偏东30°方向上,渔船不改变航向继续向东航行30海里到达点D,这是测得灯塔A在北偏西60°方向上,求灯塔A,B间的距离.(计算结果用根号表示,不取近似值)
解:
如图,由题意可得出:∠FCA=∠AC ( http: / / www.21cnjy.com )N=45°,∠NCB=30°,∠ADE=60°,过点A作AF⊥FD,垂足为F,则∠FAD=60°,∠FAC=∠FCA=45°,∠ADF=30°,∴AF=FC=AN=NC,设AF=FC=x,∴tan30°===,解得x=15(+1),∵tan30°=,∴=,解得BN=15+5,∴AB=AN+BN=15(+1)+15+5=30+20.答:灯塔A,B间的距离为(30+20)海里
第1课时 解直角三角形及其简单应用
1.在直角三角形中,由__已知__元素求出__未知__元素的过程,叫做解直角三角形.
2.在直角三角形中,除直角外还有__五__个元素,知道__两__个元素(至少有一个是边),就可以求出另外__三__个元素.
3.解直角三角形,一般是下面两种情况:(1)已知两条边;(2)已知一条边和一个__锐角__.
知识点1:已知两边解直角三角形
1.在△ABC中,∠C=90°,AC=4,AB=7,欲求∠A的值,最适宜的做法是( C )
A.计算tanA的值求出
B.计算sinA的值求出
C.计算cosA的值求出
D.先根据sinB求出∠B,再利用90°-∠B求出
2.在Rt△ABC中,∠C=90°,a=20,c=20,则∠A=__45°__,∠B=__45°__,b=__20__.
3.如图,在Rt△ABC中,∠C=90°,已知BC=3,AC=9,解此直角三角形.
解:AB=6 ∠A=30° ∠B=60°
知识点2:已知一边一锐角解直角三角形
4.在Rt△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C的对边,下列各式错误的是( B )
A.a=csinA B.b=ccosB
C.b=atanB D.a=btanA
5.(2014·杭州)在Rt△ABC中,已知∠C=90°,∠A=40°,BC=3,则AC=( D )
A.3sin40° B.3sin50°
C.3tan40° D.3tan50°
6.(2014·来宾)如图,Rt△ABC中,∠C=90°,∠B=30°,BC=6,则AB的长为__4__.
7.在Rt△ABC中,CA=CB,AB=9,点D在BC边上,连接AD,若tan∠CAD=,则BD的长为__6__.
8.在Rt△ABC中,∠C=90°,c=8,∠A=60°,解这个直角三角形.
解:∵∠A=60°,∴∠B=90°-∠A ( http: / / www.21cnjy.com )=30°.∵sinA=,∴a=c·sinA=8×sin60°=8×=12,∴b===4
知识点3:解直角三角形的简单应用
9.如图,为了测量河两岸A,B两点的距离,在与AB垂直的方向上取点C,测得AC=m,∠ACB=α,那么AB等于( C )
A.msinα B.mcosα
C.mtanα D.
10.如图,△ABC中,∠C=90°,点D在AC上,已知∠BDC=45°,BD=10,AB=20.求∠A的度数.
解:在Rt△BDC中,∵sin∠BDC=,∴BC=BD×sin∠BDC=10×sin45°=10.在Rt△ABC中,∵sin∠A===,∴∠A=30°
11.(2014·湖州)如图,已知Rt△ABC中,∠C=90°,AC=4,tanA=,则BC的长是( A )
A.2 B.8 C.2 D.4
,第11题图) ,第12题图)
12.(2014·扬州)如图,已知∠AOB ( http: / / www.21cnjy.com )=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=( C )
A.3 B.4 C.5 D.6
13.如图,在菱形ABCD中,DE⊥AB于点E,cosA=,BE=4,则tan∠DBE的值是__2__.
,第13题图) ,第14题图)
14.如图,已知在Rt△ABC中,斜边BC上的高AD=4,cosB=,则AC=__5__.
15.根据下列条件解Rt△ABC.(∠C=90°)
(1)∠A=30°,b=;
解:∠B=90°-∠A=90°-30°=60°,∵tanA=,∴a=b·tanA=×=1,∴c=2a=2
(2)c=4,b=2.
解:由勾股定理得:a===2.∵b=2,a=2,∠C=90°,∴∠A=∠B=45°
16.(2014·济宁)如图,在△ABC中,∠A=30°,∠B=45°,AC=2,求AB的长.
解:过点C作CD⊥AB于点 ( http: / / www.21cnjy.com )D,则∠ADC=∠BDC=90°.∵∠B=45°,∴∠BCD=∠B=45°,∴CD=BD.∵∠A=30°,AC=2,∴CD=,∴BD=CD=,由勾股定理得:AD==3,∴AB=AD+BD=3+
17.一个长方体木箱沿斜面下滑,当木箱 ( http: / / www.21cnjy.com )滑至如图位置时,AB=3 m.已知木箱高BE= m,斜面坡角为30°,求木箱端点E距地面AC的高度EF.
解:连接AE,在Rt△ABE中,A ( http: / / www.21cnjy.com )B=3 m,BE= m,则AE==2 m,又∵tan∠EAB==,∴∠EAB=30°,在Rt△AEF中,∠EAF=∠EAB+∠BAC=60°,∴EF=AE×sin∠EAF=2×sin60°=2×=3 m
18.探究:如图①,在△ABC中,∠A=α(0°<α<90°),AB=c,AC=b,试用含b,c,α的式子表示△ABC的面积;
应用:如图②,在 ABCD中,对角线AC,BD相交成的锐角为α,若AC=a,BD=b,试用含b,c,α的式子表示 ABCD的面积.
解:探究:过点B作BD⊥AC,垂足 ( http: / / www.21cnjy.com )为D.∵AB=c,∠A=α,∴BD=c·sinα,∴S△ABC=AC·BD=bcsinα.应用:过点C作CE⊥DO于点E.∴sinα=.∵在 ABCD中,AC=a,BD=b,∴CO=a,DO=b,∴S△COD=CO·DO·sinα=absinα,∴S△BCD=CE×BD=×asinα×b=absinα
第2课时 仰角、俯角与解直角三角形的应用
在进行测量时,从下向上看,视线与水平线的夹角叫做__仰角__;从上往下看,视线与水平线的夹角叫做__俯角__.
知识点:仰角、俯角与解直角三角形
1.(2014·株洲)孔明同学在距某电视塔塔 ( http: / / www.21cnjy.com )底水平距离500米处,看塔顶的仰角为20°(不考虑身高因素),则此塔高约为__182__米.(结果保留整数,参考数据:sin20°≈0.3420,sin70°≈0.9397,tan20°≈0.3640,tan70°≈2.7475)
,第1题图) ,第2题图)
2.如图,某飞机于空中A处 ( http: / / www.21cnjy.com )探测到地面目标B,此时从飞机看目标B的俯角α=30°,飞行高度AC=1200米,则飞机到目标B的距离AB为__2400__米.
3.(2014·襄阳)如 ( http: / / www.21cnjy.com )图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为5 m,则大树的高度为__(5+5)__m.(结果保留根号)
,第3题图) ,第4题图)
4.如图,从热气球C处测得地面A,B两 ( http: / / www.21cnjy.com )点的俯角分别是30°,45°,如果此时热气球C处的高度CD为100米,点A,D,B在同一直线上,则AB两点的距离是( D )
A.200米 B.200 米
C.220 米 D.100(+1)米
5.如图,山顶有一座电视塔,在地面上一 ( http: / / www.21cnjy.com )点A处测得塔顶B处的仰角α=60°,在塔底C处测得A点俯角β=45°,已知塔高60米,则山高CD等于( A )
A.30(1+)米 B.30(-1)米
C.30米 D.(30+1)米
6.(2014·昆明)如图,在数学 ( http: / / www.21cnjy.com )实践课中,小明为了测量学校旗杆CD的高度,在地面A处放置高度为1.5米的测角仪AB,测得旗杆顶端D的仰角为32°,AC为22米,求旗杆CD的高度.(结果精确到0.1米.参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)
解:过点B作BE⊥CD,垂足为E,在Rt ( http: / / www.21cnjy.com )△DEB中,∠DEB=90°,BE=AC=22(米),tan32°=,∴DE=BE·tan32°≈22×0.62=13.64(米).∵EC=AB=1.5,∴CD=CE+ED=1.5+13.64=15.14≈15.1(米).答:旗杆CD的高度为15.1米
7.(2014·广州)如图,某数学兴 ( http: / / www.21cnjy.com )趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10 m,到达B点,在B处测得树顶C的仰角高度为60°(A,B,D三点在同一直线上).请你根据他们测量数据计算这棵树CD的高度.(结果精确到0.1 m,参考数据:≈1.414,≈1.732)
解:∵∠CBD=∠A+∠ACB,∴∠A ( http: / / www.21cnjy.com )CB=∠CBD-∠A=60°-30°=30°,∴∠A=∠ACB,∴BC=AB=10(米).在直角△BCD中,CD=BC·sin∠CBD=10×=5≈5×1.732=8.7(米).答:这棵树CD的高度为8.7米
8.如图,小敏同学想测量一棵大 ( http: / / www.21cnjy.com )树的高度.她站在B处仰望树顶,测得仰角为30°,再往大树的方向前进4 m,测得仰角为60°,已知小敏同学身高(AB)为1.6 m,则这棵树的高度为( D )(结果精确到0.1 m,≈1.73)
A.3.5 m B.3.6 m
C.4.3 m D.5.1 m
9.(2014·自贡)如图,某学校新建 ( http: / / www.21cnjy.com )了一座吴玉章塑像,小林站在距离塑像2.7米的A处自B点看塑像头顶D的仰角为45°,看塑像底部C的仰角为30°,求塑像CD的高度.(结果精确到0.1米,参考数据:≈1.7)
解:在Rt△DEB中,DE=BE·tan4 ( http: / / www.21cnjy.com )5°=2.7米,在Rt△CEB中,CE=BE·tan30°=0.9米,则CD=DE-CE=2.7-0.9≈1.2米.故塑像CD的高度大约为1.2米
10.(2014·海南)如图 ( http: / / www.21cnjy.com ),一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行1 464米到B点处测得正前方C点处的俯角为45°.求海底C点处距离海面DF的深度.(结果精确到个位,参考数据:≈1.414,≈1.732,≈2.236)
解:作CE⊥AB于点E,依题意,AB= ( http: / / www.21cnjy.com )1 464,∠EAC=30°,∠CBE=45°,设CE=x,则BE=x,Rt△ACE中,tan30°===,整理得出:3x=1 464+x,解得x=732(+1)≈2 000米,∴x+600=2 600米.答:海底C点处距离DF的深度约为2 600米
11.(2014·哈尔滨)如图,AB, ( http: / / www.21cnjy.com )CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶部A点测建筑物CD的顶部C点的俯角∠EAC为30°.测得建筑物CD的底部D点的俯角∠EAD为45°.
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度.(结果保留根号)
解:(1)根据题意得,BD∥AE,∴∠A ( http: / / www.21cnjy.com )DB=∠EAD=45°,∵∠ABD=90°,∴∠BAD=∠ADB=45°,∴BD=AB=60,∴两建筑底部之间水平距离BD的长度为60米 (2)延长AE,DC交于点F,根据题意得四边形ABDF为正方形,∴AF=BD=DF=60,在Rt△AFC中,∠FAC=30°,∴CF=AF·tan∠FAC=60×=20,又∵FD=60,∴CD=60-20,∴建筑物CD的高度为(60-20)米
12.(2014·黔东南州)黔东南州某校九年 ( http: / / www.21cnjy.com )级某班开展数学活动,小明和小军合作用一副三角板测量学校的旗杆,小明站在B点测得旗杆顶端E点的仰角为45°,小军站在点D测得旗杆顶端E点的仰角为30°,已知小明和小军相距(BD)6米,小明的身高(AB)1.5米,小军的身高(CD)1.75米,求旗杆的高EF的长.(结果精确到0.1,参考数据:≈1.41,≈1.73)
解:过点A作AM⊥EF于点M,过点C ( http: / / www.21cnjy.com )作CN⊥EF于点N,∴MN=0.25米,∵∠EAM=45°,∴AM=ME,设AM=ME=x米,则CE=(x+6)米,EN=(x-0.25)米,∵∠ECN=30°,∴tan∠ECN===,解得x≈8.8,则EF=EN+MF≈8.8+1.5=10.3(米).答:旗杆的高EF为10.3米
第3课时 坡度与解直角三角形的应用
坡面的铅垂高度(h)和水平长度(l)的 ( http: / / www.21cnjy.com )比叫做坡面的__坡度__(或坡比),记作i,即i=____.坡度一般写成1∶m的形式.坡面与水平面的夹角叫做__坡角__,记作α,有i==__tanα__,坡度越大,坡角α就__越大__,坡面就__越陡__.
知识点1:坡度和坡角
1.(2014·怀化)如图,小明爬一土坡 ( http: / / www.21cnjy.com ),他从A处爬到B处所走的直线距离AB=4米,此时,他离地面高度为h=2米,则这个土坡的坡角∠A=__30°__.
2.某水库大坝的横断面是梯形,坝内斜坡的坡度i=1∶,坝外斜坡的坡度i=1∶1,则两个坡角的和为__75°__.
3.某人沿着有一定坡度的坡面前进了10米,此时他与水平地面的垂直距离为2 米,则这个坡面的坡度为__1∶2__.
知识点2:解有关坡度、坡角的实际问题
4.(2014·丽水)如图,河坝横 ( http: / / www.21cnjy.com )断面迎水坡AB的坡比是1∶(坡比是坡面的铅直高度BC与水平宽度AC之比),坝高BC=3 cm,则坡面AB的长度是( B )
A.9 m B.6 m C.6 m D.3 m
,第4题图) ,第5题图)
5.如图,先锋村准备在坡角为α的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为( B )
A.5cosα B.
C.5sinα D.
6.如图,斜坡AC的坡度(坡比)为1 ( http: / / www.21cnjy.com )∶,AC=10米.坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带AB相连,AB=14米.则旗杆BC的高度是__6__米.
7.(2014·巴中)如图,一水库大坝 ( http: / / www.21cnjy.com )的横断面为梯形ABCD,坝顶BC宽6米,坝高20米,斜坡AB的坡度i=1∶2.5,斜坡CD的坡角为30°,求坝底AD的长度.(精确到0.1米,参考数据:≈1.414,≈1.732.提示:坡度等于坡面的铅垂高度与水平长度之比)
解:作BE⊥AD,CF⊥AD ( http: / / www.21cnjy.com ),垂足分别为点E,F,则四边形BCFE是矩形,由题意得,BC=EF=6米,BE=CF=20米,斜坡AB的坡度i为1∶2.5,在Rt△ABE中,BE=20米,=,∴AE=50米.在Rt△CFD中,∠D=30°,∴DF=CF·cotD=20 米,∴AD=AE+EF+FD=50+6+20≈90.6(米).故坝底AD的长度约为90.6米
8.某商场为方便顾客使用购 ( http: / / www.21cnjy.com )物车,准备将滚动电梯的坡面坡度由1∶1.8改为1∶2.4(如图).如果改动后电梯的坡面长为13米,求改动后电梯水平宽度增加部分BC的长.
解:在Rt△ADC中,∵AD∶DC=1∶2 ( http: / / www.21cnjy.com ).4,AC=13,由AD2+DC2=AC2,得AD2+(2.4·AD)2=132,∴AD=5,∴DC=12米.在Rt△ABD中,∵AD∶BD=1∶1.8,∴BD=1.8·AD=9米,∴BC=DC-BD=12-9=3(米).答:改动后电梯水平宽度增加部分BC的长为3米
9.(2014·德州)如图是拦水坝的横断面,斜坡AB的水平宽度为12米,斜面坡度为1∶2,则是斜坡AB的长为( B )
A.4 米 B.6 米
C.12 米 D.24米
,第9题图) ,第10题图)
10.(2014·上海)如图,已知传送带与水 ( http: / / www.21cnjy.com )平面所成斜坡的坡度i=1∶2.4,如果它把物体送到离地面10米高的地方,那么物体所经过的路程为__26__米.
11.如图,某公园入口处原有三级台阶,每级台 ( http: / / www.21cnjy.com )阶高为18 cm,深为30 cm,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1∶5,则AC的长度是__210__cm.
12.某校教学楼后面紧邻着一 ( http: / / www.21cnjy.com )个山坡,坡上面是一块平地,如图所示,BC∥AD,BE⊥AD,斜坡AB长为 米,坡度i=9∶5.为了减缓坡面防止山体滑坡,保障安全,学校决定对该斜坡进行改造,地质人员勘测,当坡角不超过45°时,可确保山体不滑坡.
(1)求改造前坡顶到地面的距离BE的长;
(2)如果改造时保持坡脚A不动,坡顶B沿BC削进到F处,问BF至少是多少米?
解:(1)∵i==,设BE=9k,AE=5k(k为正数),则在Rt△AEB中,∠BEA=90°,AB=米,AB2=BE2+AE2,即()2=(9k)2+(5k)2,解得k=,∴BE=9×=22.5(米)(2)由(1)得AE=12.5,设BF=x,作FH⊥AD于点H,则=tan∠FAH,由题意得≤tan45°,即x≥10.所以坡顶B沿BC至少削进10米,才能确保安全
13.(2014·遵义)如图,一楼房AB后 ( http: / / www.21cnjy.com )有一假山,其坡度为i=1∶,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅垂高度与水平宽度的比)
解:过点E作EF⊥BC的延长线于点F, ( http: / / www.21cnjy.com )EH⊥AB于点H,在Rt△CEF中,∵i===tan∠ECF,∴∠ECF=30°,∴EF=CE=10米,CF=10米,∴BH=EF=10米,HE=BF=BC+CF=(25+10)米,在Rt△AHE中,∵∠HAE=45°,∴AH=HE=(25+10)米,∴AB=AH+HB=(35+10)米.答:楼房AB的高为(35+10)米
14.如图,某防洪指挥部发现长江边 ( http: / / www.21cnjy.com )一处长600米,高10米,背水坡的坡角为45°的防洪大堤(横断面为梯形ABCD)急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:背水坡面用土石进行加固,并使上底加宽3米,加固后背水坡EF的坡比i=1∶.
(1)求加固后坝底增加的宽度AF;(结果保留根号)
(2)求完成这项工程需要土石多少立方米?(结果保留根号)
解:(1)过点E,D作EM⊥BF ( http: / / www.21cnjy.com )于点M,DN⊥BF于点N,则MN=DE=2米,EM=DN=10米.在Rt△AND中,AN==10米.∵i==,∴FM=10米,∴AF=FM+MN-AN=(10-8)米 (2)∵S梯形ADEF==50-30,∴(50-30)×600≈(30000-18000)立方米.答:完成这项工程需要土石约(30000-18000)立方米
综合练习 解直角三角形的实际应用
1.如图为测量某物体AB的高度,在D点 ( http: / / www.21cnjy.com )测得A点的仰角为30°,朝物体AB方向前进20米到达点C,再次测得A点的仰角为60°,则物体的高度为( A )
A.10 米 B.10米 C.20 米 D. 米
,第1题图) ,第2题图)
2.(2014·临沂)如图,在某监 ( http: / / www.21cnjy.com )测点B处望见一艘正在作业的渔船在南偏西15°方向的A处,若渔船沿北偏西方75°方向以40海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B,C之间的距离为( C )
A.20海里 B.10 海里
C.20 海里 D.30海里
3.(2014·衡阳)如图,一河坝的 ( http: / / www.21cnjy.com )横断面为等腰梯形ABCD,坝顶宽10米,坝宽12米,斜坡AB的坡度i=1∶1.5,则坝底AD的长度为( D )
A.26米 B.28米 C.30米 D.46米
,第3题图) ,第4题图)
4.(2014·舟山)如图,在地面上的点A处测得树顶B的仰角为α度,AC=7米,则树高BC为__7tanα__米.(用含α的代数式表示)
5.如图,两建筑物的水平距离BC为18 ( http: / / www.21cnjy.com ) m,从A点测得D点的俯角α为30°,测得C点的俯角β为60°,则建筑物CD的高度为__12__m.(结果不作近似计算)
,第5题图) ,第6题图)
6.(2014·十堰)如 ( http: / / www.21cnjy.com )图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是__24__海里.(结果精确到个位,参考数据:≈1.4,≈1.7,≈2.4)
7.(2014·南京)如图,梯子斜 ( http: / / www.21cnjy.com )靠在与地面垂直(垂足为O)的墙上,当梯子位于AB位置时,它与地面所成的角∠ABO=60°;当梯子底端向右滑动1 m(即BD=1 m)到达CD的位置时,它与地面所成的角∠CDO=51°18′,求梯子的长.(参考数据:sin51°18′≈0.780,cos51°18′≈0.625,tan51°18′≈1.248)
解:设梯子的长x m.在 ( http: / / www.21cnjy.com )Rt△AOB中,cos∠ABO=,∴OB=AB·cos∠ABO=x·cos60°=x.在Rt△CDO中,cos∠CDO=,∴OD=CD·cos∠CDO=x·cos51°18′≈0.625x.∵BD=OD-OB,∴0.625x-x=1,解得x=8.故梯子的长是8米
8.(2014·烟台)小明坐于堤边 ( http: / / www.21cnjy.com )垂钓,如图,河堤AC的坡角为30°,AC的长米,钓竿AO的倾斜角是60°,其长为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离.
解:延长OA交BC于点D.∵AO ( http: / / www.21cnjy.com )的倾斜角是60°,∴∠ODB=60°.∵∠ACD=30°,∴∠CAD=180°-∠ODB-∠ODB-∠ACD=90°,在Rt△ACD中,AD=AC·tan∠ACD=·=(米),∴CD=2AD=3(米),又∵∠O=60°,∴△BOD是等边三角形,∴BD=OD=OA+AD=3+1.5=4.5(米),∴BC=BD-CD=4.5-3=1.5(米).答:浮漂B与河堤下端C之间的距离为1.5米
9.(2014·河南)在中俄“海上 ( http: / / www.21cnjy.com )联合-2014”反潜演习中,我军舰A测得潜艇C的俯角为30°.位于军舰A正上方1 000米的反潜直升机B测得潜艇C的俯角为68°.试根据以上数据求出潜艇C离开海平面的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5,≈1.7)
解:过点C作CD⊥BA的延 ( http: / / www.21cnjy.com )长线于点D.则AD即为潜艇C的下潜深度,根据题意得∠ACD=30°,∠BCD=68°.设AD=x,则BD=BA+AD=1 000+x.在Rt△ACD中,CD===x.在Rt△BCD中,BD=CD·tan68°.∴1 000+x=x·tan68°,∴x=≈≈308.∴潜艇C离开海平面的下潜深度约为308米
10.(2014·南充)马航M ( http: / / www.21cnjy.com )H370失联后,我国政府积极参与搜救.某日,我两艘专业救助船A,B同时收到有关可疑漂浮物的讯息,可疑漂浮物P在救助船A的北偏东53.5°方向上,在救助船B的西北方向上,船B在船A正东方向140海里处.(参考数据:sin36.5°≈0.6,cos36.5°≈0.8,tan36.5°≈0.75)
(1)求可疑漂浮物P到A,B两船所在直线的距离;
(2)若救助船A、救助船B分别以40海里/时,30海里/时的速度同时出发,匀速直线前往搜救,试通过计算判断哪艘船先到达P处.
解:(1)过点P作PH⊥AB于点E,由题意得 ( http: / / www.21cnjy.com ),∠PAE=36.5°,∠PBA=45°,在Rt△PAE中,=tan∠PAE=,即=0.75,解得x=60海里,∴可疑漂浮物P到A,B两船所在直线的距离为60海里 (2)在Rt△PBE中,PE=60海里,∠PBE=45°,则BP=PE=60≈84.8海里,B船需要的时间为:≈2.83小时,在Rt△PAE中,=sin∠PAE,∴AP=PE÷sin∠PAE=60÷0.6=100海里,∴A船需要的时间为:100÷40=2.5,∵2.83>2.5,∴A船先到达
11.(2014·安徽)如图,在同一 ( http: / / www.21cnjy.com )平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20 km;BC段与AB,CD段都垂直,长为10 km,CD段长为30 km,求两高速公路间的距离.(结果保留根号)
解:过B点作BE⊥l1, ( http: / / www.21cnjy.com )交l1于点E,CD于点F,l2于点G.在Rt△ABE中,BE=AB·sin30°=20×=10 km,在Rt△BCF中,BF=BC÷cos30°=10÷=km,CF=BF·sin30°=×=km,DF=CD-CF=(30-)km,在Rt△DFG中,FG=DF·sin30°=(30-)×=(15-)km,∴EG=BE+BF+FG=(25+5)km.故两高速公路间的距离为(25+5)km
12.
(2014·泸州)海中两 ( http: / / www.21cnjy.com )个灯塔A,B,其中B位于A的正东方向上,渔船跟踪鱼群由西向东航行,在点C处测得灯塔A在西北方向上,灯塔B在北偏东30°方向上,渔船不改变航向继续向东航行30海里到达点D,这是测得灯塔A在北偏西60°方向上,求灯塔A,B间的距离.(计算结果用根号表示,不取近似值)
解:
如图,由题意可得出:∠FCA=∠AC ( http: / / www.21cnjy.com )N=45°,∠NCB=30°,∠ADE=60°,过点A作AF⊥FD,垂足为F,则∠FAD=60°,∠FAC=∠FCA=45°,∠ADF=30°,∴AF=FC=AN=NC,设AF=FC=x,∴tan30°===,解得x=15(+1),∵tan30°=,∴=,解得BN=15+5,∴AB=AN+BN=15(+1)+15+5=30+20.答:灯塔A,B间的距离为(30+20)海里
