青岛版数学八年级上册2.6 等腰三角形 第3课时 课件(共15张PPT)
文档属性
| 名称 | 青岛版数学八年级上册2.6 等腰三角形 第3课时 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 150.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 17:24:23 | ||
图片预览





文档简介
(共15张PPT)
第二章 图形的轴对称
2.6 等腰三角形
第3课时
1.掌握等边三角形的性质与判定(重点)
2.能运用等边三角形的性质与判定解决相关问题
在等腰三角形中,有一种特殊的情况,就是底与腰相等,这时三角形三边相等,我们把三条边都相等的三角形叫做等边三角形,也叫正三角形.
思考:把等腰三角形的性质用于等边三角形,能得到什么结论?
由等腰三角形的性质两个底角相等,我们可以推测等边三角形三个角都相等.
(一)等边三角形的性质
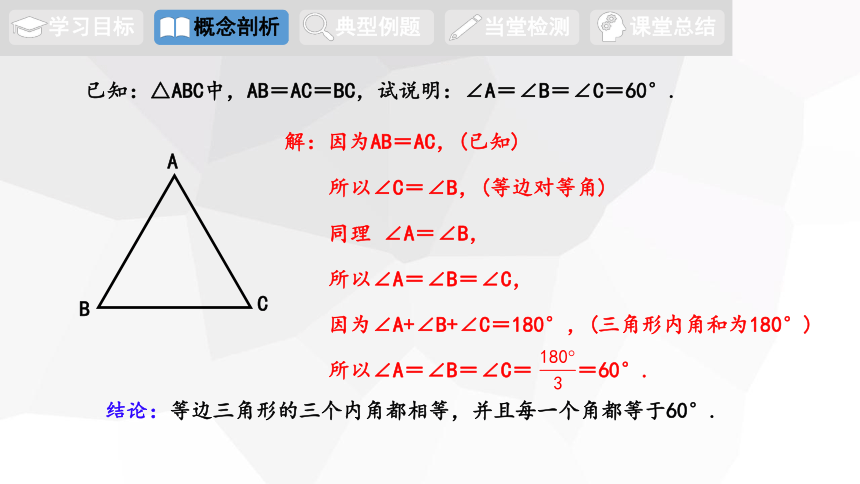
已知:△ABC中,AB=AC=BC,试说明:∠A=∠B=∠C=60°.
A
B
C
解:因为AB=AC,(已知)
因为∠A+∠B+∠C=180°,(三角形内角和为180°)
所以∠A=∠B=∠C= =60°.
所以∠C=∠B,(等边对等角)
同理 ∠A=∠B,
所以∠A=∠B=∠C,
结论:等边三角形的三个内角都相等,并且每一个角都等于60°.
等腰三角形有“三线合一”的性质,等边三角形有“三线合一”的性质吗?
等边三角形是特殊的等腰三角形,三条边的长度相等,故而等腰三角形“三线合一”的性质在等边三角形中适用,且“三线合一”的性质对每条边都适用,
所以等边三角形“三线合一”的性质可以进一步表述为:
每一边上的中线、高和这一边所对的角的平分线互相重合.
同理,等边三角形有3条对称轴.
解:因为△ABC是等边三角形,BD是中线,
所以∠CDE=∠CED,
所以∠CDE=∠CED= ∠BCD=30°,
例1.如图,△ABC是等边三角形,BD是中线,延长BC至E,CE=CD,试说明:DB=DE.
所以∠ABC=∠ACB=60°,∠DBC=30°.
又因为CE=CD,
又因为∠BCD=∠CDE+∠CED,
所以∠DBC=∠DEC.
所以DB=DE(等角对等边).
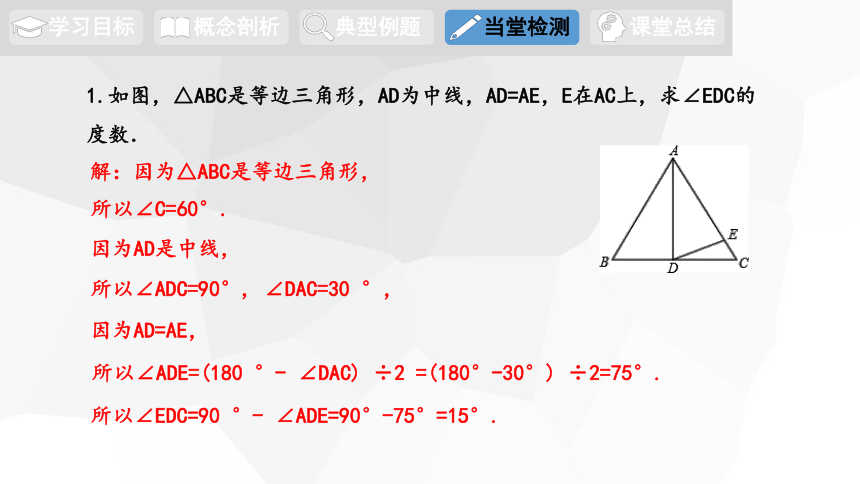
1.如图,△ABC是等边三角形,AD为中线,AD=AE,E在AC上,求∠EDC的度数.
解:因为△ABC是等边三角形,
所以∠C=60°.
因为AD是中线,
所以∠ADC=90°, ∠DAC=30 °,
因为AD=AE,
所以∠ADE=(180 °- ∠DAC) ÷2 =(180°-30°) ÷2=75°.
所以∠EDC=90 °- ∠ADE=90°-75°=15°.
A
B
C
已知:△ABC中,∠A=∠B=∠C = 60°,求证:AB=AC=BC.
所以AC=BC,(等边对等角)
解:因为∠A=∠B,(已知)
同理 AB=AC,
所以AB=BC=AC,
所以△ABC是等边三角形.
结论:三个角都相等的三角形是等边三角形.
一个三角形的三个内角满足什么条件才是等边三角形?
①三条边相等的三角形是等边三角形,那三个角都相等的三角形是等边三角形吗?
(二)等边三角形的判定
②有一个角是60°的等腰三角形是等边三角形吗?
已知:等腰三角形ABC中,存在一个角为60°,试说明:△ABC是等边三角形.
A
B
C
解:当60°角为底角时,
因为等腰三角形两个底角相等,
所以三角形的顶角为180°-60°×2=60°,
所以该三角形是等边三角形(三个角都相等的三角形是等边三角形),
同理:当60°角是顶角时,三个内角相等均为60°,
所以有一个角是60°的等腰三角形是等边三角形.
性质1:等边三角形的三个内角都相等,并且每一个角都等于60°.
判定1:三个角都相等的三角形是等边三角形.
归纳:
性质2:等边三角形每一边上的中线、高和这一边所对的角的平分线互相重合.
判定2:有一个角是60°的等腰三角形是等边三角形.
性质3:等边三角形有3条对称轴.
例2.如图,在等边三角形ABC中,DE∥BC,试说明:△ADE是等边三角形.
分析:结合平行线的性质,说明三个角相等即可说明三角形为等边三角形.
A
C
B
D
E
解:
因为△ABC是等边三角形,
所以∠A=∠B=∠C.
因为DE//BC,
所以∠ADE=∠B, ∠AED=∠C.
所以∠A=∠ADE=∠AED.
所以△ADE是等边三角形.
2.已知:如图,△ABO是等边三角形,CD∥AB,分别交AO、BO的延长线于点C、D.试说明:△OCD是等边三角形.
解:因为△ABO是等边三角形,
所以∠A=∠B=∠AOB=60°,
因为AB∥CD,
所以∠C=∠A=60°,∠D=∠B=60°,
因为∠COD=∠AOB=60°,
所以∠C=∠D=∠COD,
所以△OCD是等边三角形.
例3.如图,△ABC是等边三角形,AD是高,并且AB恰好是DE的垂直平分线,试说明:△ADE是等边三角形.
解:因为AB是DE的垂直平分线,
所以AE=AD,
所以△ADE是等腰三角形,
因为AB⊥DE,
所以∠ADE=90°-∠BAD,
因为AD⊥BD,
所以∠B=90°-∠BAD,
所以∠ADE=∠B=60°,
所以△ADE是等边三角形.
(有一个角是60°的等腰三角形是等边三角形)
3.已知:如图,AB=BC,∠CDE=120°,DF∥BA,且DF平分∠CDE,试说明:△ABC是等边三角形.
因为DF∥BA,
所以∠ABC=∠CDF=60°,
因为AB=BC,
所以△ABC是等边三角形.(有一个角是60°的等腰三角形是等边三角形)
解:因为DF平分∠CDE,∠CDE=120°,
所以∠CDF=∠EDF=60°,
等边三角形的性质
等边三角形的判定
第二章 图形的轴对称
2.6 等腰三角形
第3课时
1.掌握等边三角形的性质与判定(重点)
2.能运用等边三角形的性质与判定解决相关问题
在等腰三角形中,有一种特殊的情况,就是底与腰相等,这时三角形三边相等,我们把三条边都相等的三角形叫做等边三角形,也叫正三角形.
思考:把等腰三角形的性质用于等边三角形,能得到什么结论?
由等腰三角形的性质两个底角相等,我们可以推测等边三角形三个角都相等.
(一)等边三角形的性质
已知:△ABC中,AB=AC=BC,试说明:∠A=∠B=∠C=60°.
A
B
C
解:因为AB=AC,(已知)
因为∠A+∠B+∠C=180°,(三角形内角和为180°)
所以∠A=∠B=∠C= =60°.
所以∠C=∠B,(等边对等角)
同理 ∠A=∠B,
所以∠A=∠B=∠C,
结论:等边三角形的三个内角都相等,并且每一个角都等于60°.
等腰三角形有“三线合一”的性质,等边三角形有“三线合一”的性质吗?
等边三角形是特殊的等腰三角形,三条边的长度相等,故而等腰三角形“三线合一”的性质在等边三角形中适用,且“三线合一”的性质对每条边都适用,
所以等边三角形“三线合一”的性质可以进一步表述为:
每一边上的中线、高和这一边所对的角的平分线互相重合.
同理,等边三角形有3条对称轴.
解:因为△ABC是等边三角形,BD是中线,
所以∠CDE=∠CED,
所以∠CDE=∠CED= ∠BCD=30°,
例1.如图,△ABC是等边三角形,BD是中线,延长BC至E,CE=CD,试说明:DB=DE.
所以∠ABC=∠ACB=60°,∠DBC=30°.
又因为CE=CD,
又因为∠BCD=∠CDE+∠CED,
所以∠DBC=∠DEC.
所以DB=DE(等角对等边).
1.如图,△ABC是等边三角形,AD为中线,AD=AE,E在AC上,求∠EDC的度数.
解:因为△ABC是等边三角形,
所以∠C=60°.
因为AD是中线,
所以∠ADC=90°, ∠DAC=30 °,
因为AD=AE,
所以∠ADE=(180 °- ∠DAC) ÷2 =(180°-30°) ÷2=75°.
所以∠EDC=90 °- ∠ADE=90°-75°=15°.
A
B
C
已知:△ABC中,∠A=∠B=∠C = 60°,求证:AB=AC=BC.
所以AC=BC,(等边对等角)
解:因为∠A=∠B,(已知)
同理 AB=AC,
所以AB=BC=AC,
所以△ABC是等边三角形.
结论:三个角都相等的三角形是等边三角形.
一个三角形的三个内角满足什么条件才是等边三角形?
①三条边相等的三角形是等边三角形,那三个角都相等的三角形是等边三角形吗?
(二)等边三角形的判定
②有一个角是60°的等腰三角形是等边三角形吗?
已知:等腰三角形ABC中,存在一个角为60°,试说明:△ABC是等边三角形.
A
B
C
解:当60°角为底角时,
因为等腰三角形两个底角相等,
所以三角形的顶角为180°-60°×2=60°,
所以该三角形是等边三角形(三个角都相等的三角形是等边三角形),
同理:当60°角是顶角时,三个内角相等均为60°,
所以有一个角是60°的等腰三角形是等边三角形.
性质1:等边三角形的三个内角都相等,并且每一个角都等于60°.
判定1:三个角都相等的三角形是等边三角形.
归纳:
性质2:等边三角形每一边上的中线、高和这一边所对的角的平分线互相重合.
判定2:有一个角是60°的等腰三角形是等边三角形.
性质3:等边三角形有3条对称轴.
例2.如图,在等边三角形ABC中,DE∥BC,试说明:△ADE是等边三角形.
分析:结合平行线的性质,说明三个角相等即可说明三角形为等边三角形.
A
C
B
D
E
解:
因为△ABC是等边三角形,
所以∠A=∠B=∠C.
因为DE//BC,
所以∠ADE=∠B, ∠AED=∠C.
所以∠A=∠ADE=∠AED.
所以△ADE是等边三角形.
2.已知:如图,△ABO是等边三角形,CD∥AB,分别交AO、BO的延长线于点C、D.试说明:△OCD是等边三角形.
解:因为△ABO是等边三角形,
所以∠A=∠B=∠AOB=60°,
因为AB∥CD,
所以∠C=∠A=60°,∠D=∠B=60°,
因为∠COD=∠AOB=60°,
所以∠C=∠D=∠COD,
所以△OCD是等边三角形.
例3.如图,△ABC是等边三角形,AD是高,并且AB恰好是DE的垂直平分线,试说明:△ADE是等边三角形.
解:因为AB是DE的垂直平分线,
所以AE=AD,
所以△ADE是等腰三角形,
因为AB⊥DE,
所以∠ADE=90°-∠BAD,
因为AD⊥BD,
所以∠B=90°-∠BAD,
所以∠ADE=∠B=60°,
所以△ADE是等边三角形.
(有一个角是60°的等腰三角形是等边三角形)
3.已知:如图,AB=BC,∠CDE=120°,DF∥BA,且DF平分∠CDE,试说明:△ABC是等边三角形.
因为DF∥BA,
所以∠ABC=∠CDF=60°,
因为AB=BC,
所以△ABC是等边三角形.(有一个角是60°的等腰三角形是等边三角形)
解:因为DF平分∠CDE,∠CDE=120°,
所以∠CDF=∠EDF=60°,
等边三角形的性质
等边三角形的判定
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
