青岛版七年级数学下册14.3 直角坐标系中的图形 第2课时 课件 (共17张PPT)
文档属性
| 名称 | 青岛版七年级数学下册14.3 直角坐标系中的图形 第2课时 课件 (共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1003.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 17:30:36 | ||
图片预览





文档简介
(共17张PPT)
第2课时
14.3 直角坐标系中的图形
第十四章 位置与坐标
1.对于一个图形,能建立合适的坐标系表示图形上各点的坐标;
2.经历探索图形的平移与图形各个点的坐标变化之间关系的过程,能应用二者关系解决图形的平移问题.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
知识点一:建合适的坐标系
如图,有一个长方形的游泳池,南北长50米,东西宽20米.小亮站在游泳池的西北角上,小莹位于游泳池的中心位置.你能利用坐标确定小亮和小莹的位置吗?
小亮
小莹
50米
20米
北
典型例题
当堂检测
学习目标
课堂总结
概念剖析
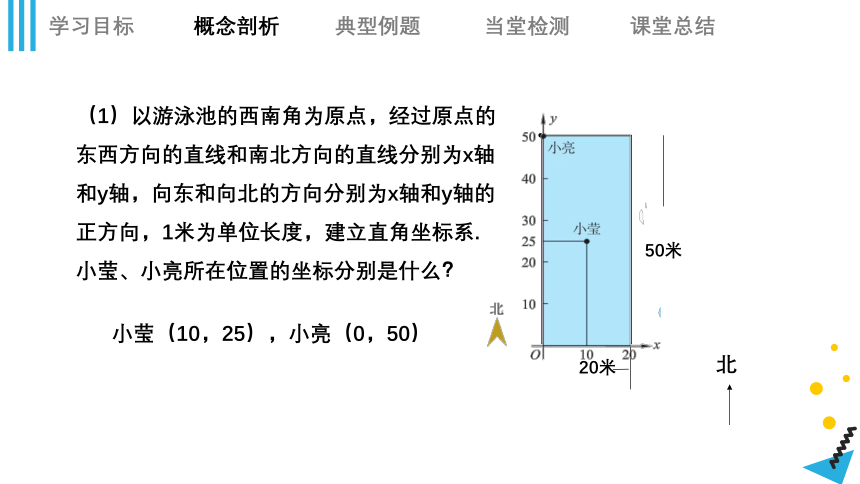
(1)以游泳池的西南角为原点,经过原点的东西方向的直线和南北方向的直线分别为x轴和y轴,向东和向北的方向分别为x轴和y轴的正方向,1米为单位长度,建立直角坐标系.小莹、小亮所在位置的坐标分别是什么?
小亮
小莹
50米
20米
北
小莹(10,25),小亮(0,50)
典型例题
当堂检测
学习目标
课堂总结
概念剖析
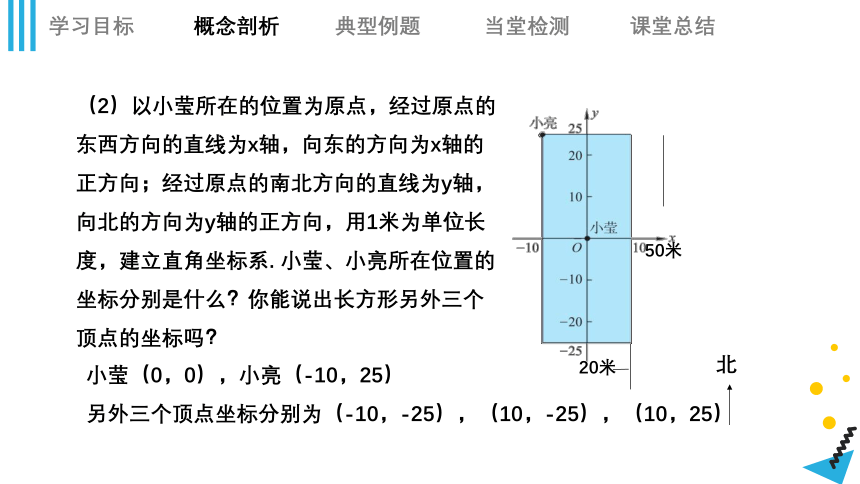
(2)以小莹所在的位置为原点,经过原点的东西方向的直线为x轴,向东的方向为x轴的正方向;经过原点的南北方向的直线为y轴,向北的方向为y轴的正方向,用1米为单位长度,建立直角坐标系. 小莹、小亮所在位置的坐标分别是什么?你能说出长方形另外三个顶点的坐标吗?
小亮
小莹
50米
20米
北
小莹(0,0),小亮(-10,25)
另外三个顶点坐标分别为(-10,-25),(10,-25),(10,25)
典型例题
当堂检测
学习目标
课堂总结
概念剖析
归纳总结:
建立平面直角坐标系,一般要使图形上的点的坐标容易确定,例如以长方形的两条边所在的直线为坐标轴,建立平面直角坐标系,又如以长方形的中心为原点建立平面直角坐标系.需要说明的是,虽然建立不同的平面直角坐标系,同一个点会有不同的坐标,但长方形的形状和性质不会改变.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
知识点二:图形的平移
将正方形四个顶点的横坐标都加上5,纵坐标不变,分别得到点A1、B1、C1、D1,依次连接A1、B1、C1、D1各点,所得的正方形A1B1C1D1与原正方形的大小、形状、位置有什么关系?
大小、形状完全相同
1
3
5
2
4
-1
-2
-3
-4
-5
O
3
4
2
-1
5
-2
-3
-4
-5
1
y
x
B
C
D
B1
C1
D1
A1
A
1
2
正方形A1B1C1D1可以看作将正方形ABCD向右平移5个单位长度得到.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1
3
5
2
4
-1
-2
-3
-4
-5
O
3
4
2
-1
5
-2
-3
-4
-5
1
y
x
B
C
D
A2
B2
C2
D2
A
1
3
大小、形状完全相同
正方形A2B2C2D2可以看作将正方形ABCD向上平移6个单位长度得到.
将正方形四个顶点的纵坐标都加上5,横坐标不变,分别得到点A2、B2、C2、D2,依次连接A2、B2、C2、D2各点,所得的正方形A2B2C2D2与原正方形的大小、形状、位置有什么关系?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
归纳总结:
一般地,在平面直角坐标系中,
如果把一个图形各个点的横坐标都加(或减去)一个正数a,相应的图形就是把原图形向右(或向左)平移a个单位长度;
如果把一个图形各个点的纵坐标都加(或减去)一个正数a,相应的图形就是把原图形向上(或向下)平移a个单位长度.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例1.某地为了发展城市群,在现有的四个中小城市A,B,C,D附近新建机场E,试建立适当的直角坐标系,并写出各点的坐标.
E
D
C
B
A
y
解:答案不唯一,
x
可以以点A为坐标原点,建立平面直角坐标系.
此时:A(0,0),
B(11,2),
C(11,9),
D(6,7),
E(2,10).
o
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.右图是一个围棋棋盘(局部),把这个围棋棋盘放置在一个平面直角坐标系中,白棋①的坐标是(-2,-1),求黑棋 、白棋③的坐标.
解:由已知白棋①的坐标是(-2,-1)构建平面直角坐标系,如图:
y
x
y轴应在从左往右数的第四条格线上,且向上为正方向,
x轴在从上往下数第二条格线上,且向右为正方向,
这两条直线的交点为坐标原点,
由此可得黑棋 (1,-2)、
白棋③(-1,-3).
o
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例2.在平面直角坐标系中,△ABC三个顶点的位置如图(每个小正方形的边长均为1).请画出△ABC沿x轴向右平移3个单位长度,再沿y轴向下平移2个单位长度后的△A'B'C'(其中A'、B'、C'分别是A、B、C的对应点,不写作法),写出A'、B'、C'三点的坐标.
A'
B'
C'
解:A'(0,1);
B'(-1,-1);
C'(4,-4).
典型例题
当堂检测
学习目标
课堂总结
概念剖析
总结:
(1)平移作图一般是根据题目条件作出图形中某些特殊点平移后的点,再连接得到平移后的图形;
(2)在平面直角坐标系内,图形的平移变换规律:图形上任意一点(x,y)沿x轴向右(左)平移a个单位,同时沿y轴向上(下)平移b个单位,得到对应点的坐标为(x±a,y±b).
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.如图,三角形ABC三个顶点的坐标分别是A(4,3),B(3,1),C(1,2).
(1)把三角形ABC向左平移6个单位长度,则点A的对应点A1的坐标是( , ),点B的对应点B1的坐标是( , ),点C的对应点C1的坐标是( , ),在图中画出平移后的三角形A1B1C1;
-2
3
-3
1
-5
2
A1
B1
C1
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.如图,三角形ABC三个顶点的坐标分别是A(4,3),B(3,1),C(1,2).
(2)把三角形ABC向下平移5个单位长度,则点A的对应点A2的坐标是( ,-2),点B的对应点B2的坐标是( , ),点C的对应点C2的坐标是( , ),在图中画出平移后的三角形A2B2C2.
4
3
-4
1
-3
A2
B2
C2
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3.如图,在△AOB中,A、B两点的坐标分别为(2,5)、(6,2),把△AOB向下平移3个单位,再向左平移2个单位,得到△CDE.写出C、D、E三点的坐标,并在图中画出△CDE.
C
D
E
解:C(0,2)、
E(4,-1).
D(-2,-3)、
典型例题
当堂检测
学习目标
课堂总结
概念剖析
平面直角坐标系
建立合适的平面直角坐标系
图形的平移
第2课时
14.3 直角坐标系中的图形
第十四章 位置与坐标
1.对于一个图形,能建立合适的坐标系表示图形上各点的坐标;
2.经历探索图形的平移与图形各个点的坐标变化之间关系的过程,能应用二者关系解决图形的平移问题.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
知识点一:建合适的坐标系
如图,有一个长方形的游泳池,南北长50米,东西宽20米.小亮站在游泳池的西北角上,小莹位于游泳池的中心位置.你能利用坐标确定小亮和小莹的位置吗?
小亮
小莹
50米
20米
北
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(1)以游泳池的西南角为原点,经过原点的东西方向的直线和南北方向的直线分别为x轴和y轴,向东和向北的方向分别为x轴和y轴的正方向,1米为单位长度,建立直角坐标系.小莹、小亮所在位置的坐标分别是什么?
小亮
小莹
50米
20米
北
小莹(10,25),小亮(0,50)
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(2)以小莹所在的位置为原点,经过原点的东西方向的直线为x轴,向东的方向为x轴的正方向;经过原点的南北方向的直线为y轴,向北的方向为y轴的正方向,用1米为单位长度,建立直角坐标系. 小莹、小亮所在位置的坐标分别是什么?你能说出长方形另外三个顶点的坐标吗?
小亮
小莹
50米
20米
北
小莹(0,0),小亮(-10,25)
另外三个顶点坐标分别为(-10,-25),(10,-25),(10,25)
典型例题
当堂检测
学习目标
课堂总结
概念剖析
归纳总结:
建立平面直角坐标系,一般要使图形上的点的坐标容易确定,例如以长方形的两条边所在的直线为坐标轴,建立平面直角坐标系,又如以长方形的中心为原点建立平面直角坐标系.需要说明的是,虽然建立不同的平面直角坐标系,同一个点会有不同的坐标,但长方形的形状和性质不会改变.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
知识点二:图形的平移
将正方形四个顶点的横坐标都加上5,纵坐标不变,分别得到点A1、B1、C1、D1,依次连接A1、B1、C1、D1各点,所得的正方形A1B1C1D1与原正方形的大小、形状、位置有什么关系?
大小、形状完全相同
1
3
5
2
4
-1
-2
-3
-4
-5
O
3
4
2
-1
5
-2
-3
-4
-5
1
y
x
B
C
D
B1
C1
D1
A1
A
1
2
正方形A1B1C1D1可以看作将正方形ABCD向右平移5个单位长度得到.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1
3
5
2
4
-1
-2
-3
-4
-5
O
3
4
2
-1
5
-2
-3
-4
-5
1
y
x
B
C
D
A2
B2
C2
D2
A
1
3
大小、形状完全相同
正方形A2B2C2D2可以看作将正方形ABCD向上平移6个单位长度得到.
将正方形四个顶点的纵坐标都加上5,横坐标不变,分别得到点A2、B2、C2、D2,依次连接A2、B2、C2、D2各点,所得的正方形A2B2C2D2与原正方形的大小、形状、位置有什么关系?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
归纳总结:
一般地,在平面直角坐标系中,
如果把一个图形各个点的横坐标都加(或减去)一个正数a,相应的图形就是把原图形向右(或向左)平移a个单位长度;
如果把一个图形各个点的纵坐标都加(或减去)一个正数a,相应的图形就是把原图形向上(或向下)平移a个单位长度.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例1.某地为了发展城市群,在现有的四个中小城市A,B,C,D附近新建机场E,试建立适当的直角坐标系,并写出各点的坐标.
E
D
C
B
A
y
解:答案不唯一,
x
可以以点A为坐标原点,建立平面直角坐标系.
此时:A(0,0),
B(11,2),
C(11,9),
D(6,7),
E(2,10).
o
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.右图是一个围棋棋盘(局部),把这个围棋棋盘放置在一个平面直角坐标系中,白棋①的坐标是(-2,-1),求黑棋 、白棋③的坐标.
解:由已知白棋①的坐标是(-2,-1)构建平面直角坐标系,如图:
y
x
y轴应在从左往右数的第四条格线上,且向上为正方向,
x轴在从上往下数第二条格线上,且向右为正方向,
这两条直线的交点为坐标原点,
由此可得黑棋 (1,-2)、
白棋③(-1,-3).
o
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例2.在平面直角坐标系中,△ABC三个顶点的位置如图(每个小正方形的边长均为1).请画出△ABC沿x轴向右平移3个单位长度,再沿y轴向下平移2个单位长度后的△A'B'C'(其中A'、B'、C'分别是A、B、C的对应点,不写作法),写出A'、B'、C'三点的坐标.
A'
B'
C'
解:A'(0,1);
B'(-1,-1);
C'(4,-4).
典型例题
当堂检测
学习目标
课堂总结
概念剖析
总结:
(1)平移作图一般是根据题目条件作出图形中某些特殊点平移后的点,再连接得到平移后的图形;
(2)在平面直角坐标系内,图形的平移变换规律:图形上任意一点(x,y)沿x轴向右(左)平移a个单位,同时沿y轴向上(下)平移b个单位,得到对应点的坐标为(x±a,y±b).
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.如图,三角形ABC三个顶点的坐标分别是A(4,3),B(3,1),C(1,2).
(1)把三角形ABC向左平移6个单位长度,则点A的对应点A1的坐标是( , ),点B的对应点B1的坐标是( , ),点C的对应点C1的坐标是( , ),在图中画出平移后的三角形A1B1C1;
-2
3
-3
1
-5
2
A1
B1
C1
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.如图,三角形ABC三个顶点的坐标分别是A(4,3),B(3,1),C(1,2).
(2)把三角形ABC向下平移5个单位长度,则点A的对应点A2的坐标是( ,-2),点B的对应点B2的坐标是( , ),点C的对应点C2的坐标是( , ),在图中画出平移后的三角形A2B2C2.
4
3
-4
1
-3
A2
B2
C2
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3.如图,在△AOB中,A、B两点的坐标分别为(2,5)、(6,2),把△AOB向下平移3个单位,再向左平移2个单位,得到△CDE.写出C、D、E三点的坐标,并在图中画出△CDE.
C
D
E
解:C(0,2)、
E(4,-1).
D(-2,-3)、
典型例题
当堂检测
学习目标
课堂总结
概念剖析
平面直角坐标系
建立合适的平面直角坐标系
图形的平移
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
