青岛版数学八年级上册2.2 轴对称的基本性质 第1课时 课件(共15张PPT)
文档属性
| 名称 | 青岛版数学八年级上册2.2 轴对称的基本性质 第1课时 课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 17:34:59 | ||
图片预览



文档简介
(共15张PPT)
第二章 图形的轴对称
2.2 轴对称的基本性质
1.能掌握对应点、对应线段、对应角等概念
2.能作出简单平面图形经过轴对称后的图形
3.能掌握轴对称图形或两个成轴对称的图形的对应性质
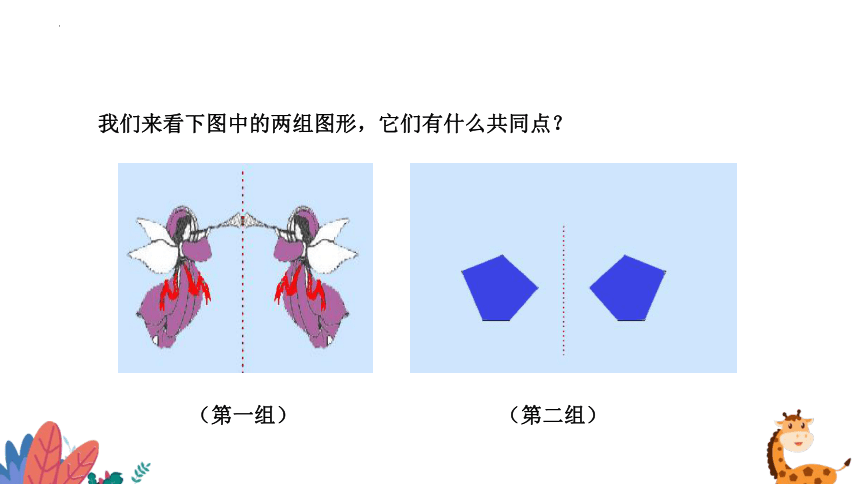
我们来看下图中的两组图形,它们有什么共同点?
(第一组)
(第二组)
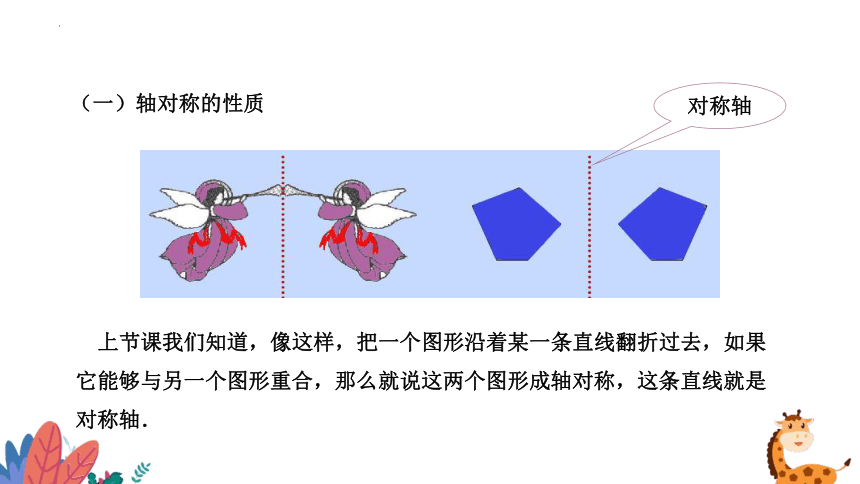
(一)轴对称的性质
上节课我们知道,像这样,把一个图形沿着某一条直线翻折过去,如果它能够与另一个图形重合,那么就说这两个图形成轴对称,这条直线就是对称轴.
对称轴
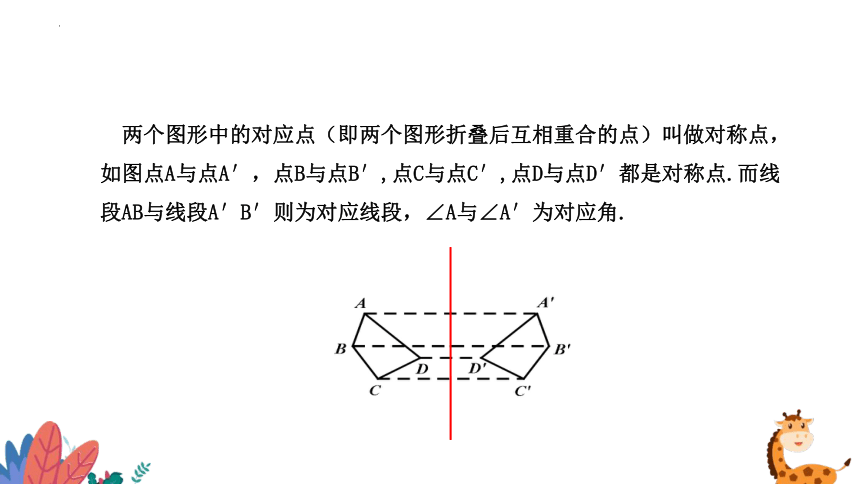
两个图形中的对应点(即两个图形折叠后互相重合的点)叫做对称点,如图点A与点A′,点B与点B′,点C与点C′,点D与点D′都是对称点.而线段AB与线段A′B′则为对应线段,∠A与∠A′为对应角.
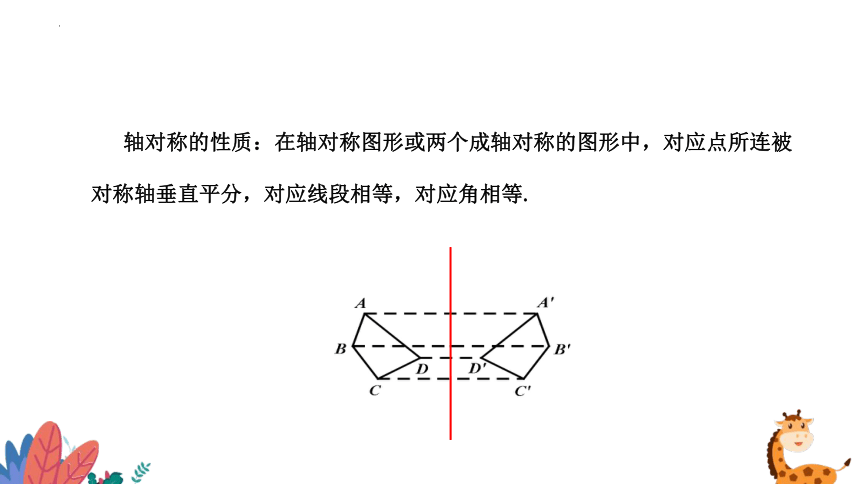
轴对称的性质:在轴对称图形或两个成轴对称的图形中,对应点所连被对称轴垂直平分,对应线段相等,对应角相等.
解:EM=DM,理由如下:
因为△ABM和△ACM关于直线AM对称,
所以∠B=∠C,BM=CM,
在△BME与△CMD中
所以△BME≌△CMD(ASA),
所以EM=DM.
技巧:利用轴对称图形的性质成轴对称的两个图形全等,对称轴垂直平分对称点的连线,进而推导对应的线段、角相等.
例1.如图,已知△ABM和△ACM关于直线AM对称,延长BM、CM,分别交AC、AB于点D、E.请找出图中与DM一定相等的线段,并说明理由.
1.如图,一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,则∠BCD的度数是( )
A.130° B.150°
C.40° D.65°
A
2.如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为 .
解析:根据正方形的轴对称性可得,阴影部分的面积等于正方形ABCD面积的一半.
因为正方形ABCD的边长为4cm,
所以S阴影=4 ÷2=8(cm ).
8cm
(二)作轴对称图形
几何图形都可以看作由点组成.对于某些图形,只要作出图形中一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.
O1
A1
B1
C1
A
B
C
例2.如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形.
分析:△ABC可以由三个顶点的位置确定,只要能分别画出这三个顶点关于直线l的对称点,连接这些对称点,就能得到要画的图形.
作法:(1)过点A画直线l的垂线,垂足为点O,在垂线上截取OA′=OA,A′就是点A关于直线l的对称点.
(2)同理,分别画出点B,C关于直线l的对称点B′,C′ .
(3)连接A′B′,B′C′,C′A′,得到△ A′B′C′即为所求.
A
B
C
A′
B′
C′
O
例2.如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形.
方法归纳:作一个图形关于一条已知直线的对称图形,关键是作出图形上一些点关于这条直线的对称点,然后再根据已知图形将这些点连接起来.
3.如图,把下列图形补成关于直线l的对称图形.
4.在3×3的正方形格点图中,有格点△ABC和△DEF,且△ABC和△DEF关于某直线成轴对称,请在下面给出的图中画出4个这样的△DEF.
A
B
C
A
B
C
A
B
C
A
B
C
(F)
(D)
E
(E)
F
D
(F)
D
E
(D)
(E)
F
2.作轴对称图形
方法:(1)找特征点;(2)作垂线;(3)截取等长;(4)依次连线.
1.轴对称的性质
在轴对称图形或两个成轴对称的图形中,对应点的连线被对称轴垂直平分,对应线段相等,对应角相等.
第二章 图形的轴对称
2.2 轴对称的基本性质
1.能掌握对应点、对应线段、对应角等概念
2.能作出简单平面图形经过轴对称后的图形
3.能掌握轴对称图形或两个成轴对称的图形的对应性质
我们来看下图中的两组图形,它们有什么共同点?
(第一组)
(第二组)
(一)轴对称的性质
上节课我们知道,像这样,把一个图形沿着某一条直线翻折过去,如果它能够与另一个图形重合,那么就说这两个图形成轴对称,这条直线就是对称轴.
对称轴
两个图形中的对应点(即两个图形折叠后互相重合的点)叫做对称点,如图点A与点A′,点B与点B′,点C与点C′,点D与点D′都是对称点.而线段AB与线段A′B′则为对应线段,∠A与∠A′为对应角.
轴对称的性质:在轴对称图形或两个成轴对称的图形中,对应点所连被对称轴垂直平分,对应线段相等,对应角相等.
解:EM=DM,理由如下:
因为△ABM和△ACM关于直线AM对称,
所以∠B=∠C,BM=CM,
在△BME与△CMD中
所以△BME≌△CMD(ASA),
所以EM=DM.
技巧:利用轴对称图形的性质成轴对称的两个图形全等,对称轴垂直平分对称点的连线,进而推导对应的线段、角相等.
例1.如图,已知△ABM和△ACM关于直线AM对称,延长BM、CM,分别交AC、AB于点D、E.请找出图中与DM一定相等的线段,并说明理由.
1.如图,一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,则∠BCD的度数是( )
A.130° B.150°
C.40° D.65°
A
2.如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为 .
解析:根据正方形的轴对称性可得,阴影部分的面积等于正方形ABCD面积的一半.
因为正方形ABCD的边长为4cm,
所以S阴影=4 ÷2=8(cm ).
8cm
(二)作轴对称图形
几何图形都可以看作由点组成.对于某些图形,只要作出图形中一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.
O1
A1
B1
C1
A
B
C
例2.如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形.
分析:△ABC可以由三个顶点的位置确定,只要能分别画出这三个顶点关于直线l的对称点,连接这些对称点,就能得到要画的图形.
作法:(1)过点A画直线l的垂线,垂足为点O,在垂线上截取OA′=OA,A′就是点A关于直线l的对称点.
(2)同理,分别画出点B,C关于直线l的对称点B′,C′ .
(3)连接A′B′,B′C′,C′A′,得到△ A′B′C′即为所求.
A
B
C
A′
B′
C′
O
例2.如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形.
方法归纳:作一个图形关于一条已知直线的对称图形,关键是作出图形上一些点关于这条直线的对称点,然后再根据已知图形将这些点连接起来.
3.如图,把下列图形补成关于直线l的对称图形.
4.在3×3的正方形格点图中,有格点△ABC和△DEF,且△ABC和△DEF关于某直线成轴对称,请在下面给出的图中画出4个这样的△DEF.
A
B
C
A
B
C
A
B
C
A
B
C
(F)
(D)
E
(E)
F
D
(F)
D
E
(D)
(E)
F
2.作轴对称图形
方法:(1)找特征点;(2)作垂线;(3)截取等长;(4)依次连线.
1.轴对称的性质
在轴对称图形或两个成轴对称的图形中,对应点的连线被对称轴垂直平分,对应线段相等,对应角相等.
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
