青岛版八年级数学上册1.2 怎样判定三角形全等 第2课时课件 (共14张PPT)
文档属性
| 名称 | 青岛版八年级数学上册1.2 怎样判定三角形全等 第2课时课件 (共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 145.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 00:00:00 | ||
图片预览




文档简介
(共14张PPT)
第一章 全等三角形
1.2 怎样判定三角形全等
第2课时
1.掌握判定三角形全等的方式——角边角、角角边
2.会通过三角形全等来说明线段相等或角相等
本节课探究一个三角形的两个角和一条边的情形,存在以下两种情况.
如图1,两个角和它们的夹边.
如图2,两个角及其中一角的对边.
A
B
C
图1
A
B
C
图2
(一)两个角和它们的夹边
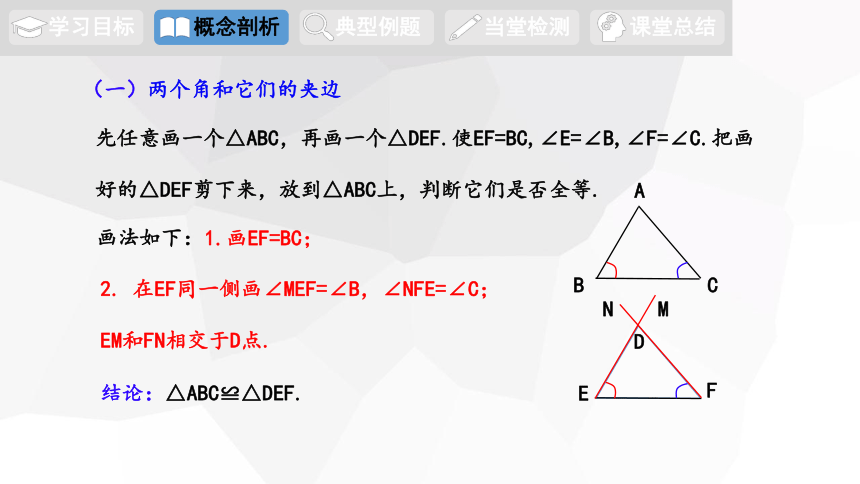
先任意画一个△ABC,再画一个△DEF.使EF=BC,∠E=∠B,∠F=∠C.把画好的△DEF剪下来,放到△ABC上,判断它们是否全等.
画法如下:
A
B
C
1.画EF=BC;
2. 在EF同一侧画∠MEF=∠B,∠NFE=∠C;
EM和FN相交于D点.
D
E
F
结论:△ABC≌△DEF.
M
N
通过探究过程我们就可以得出以下结论,用它可以判定两个三角形全等.
也就是说,三角形两个角的大小和它们夹边的长度确定了,
那么这个三角形大小、形状就确定了.
两角和它们的夹边分别相等的两个三角形全等.
(可以简写为“角边角”或“ASA”)
角边角定理
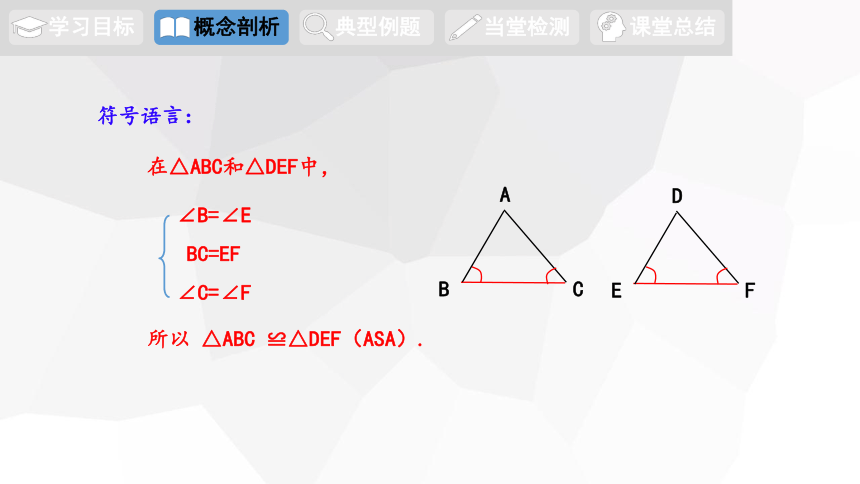
符号语言:
在△ABC和△DEF中,
所以 △ABC ≌△DEF(ASA).
∠B=∠E
BC=EF
∠C=∠F
A
B
C
D
E
F
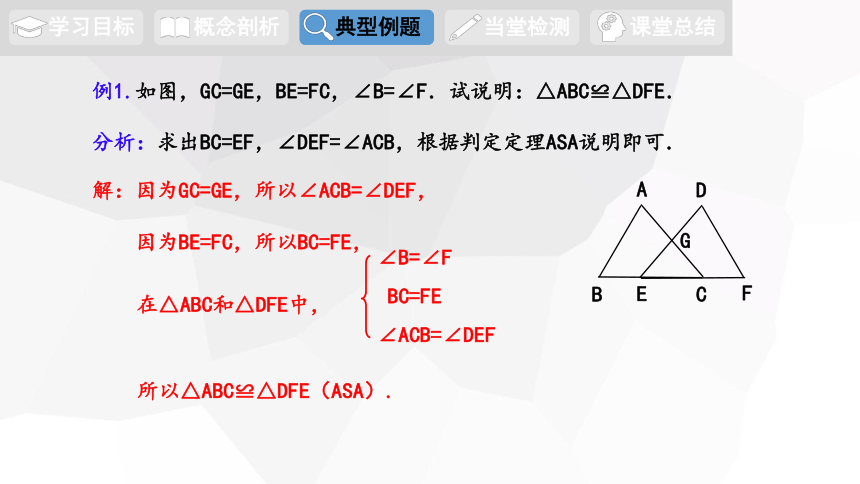
例1.如图,GC=GE,BE=FC,∠B=∠F.试说明:△ABC≌△DFE.
解:因为GC=GE,所以∠ACB=∠DEF,
因为BE=FC,所以BC=FE,
分析:求出BC=EF,∠DEF=∠ACB,根据判定定理ASA说明即可.
∠B=∠F
BC=FE
∠ACB=∠DEF
所以△ABC≌△DFE(ASA).
在△ABC和△DFE中,
A
B
C
G
E
D
F
1.如图,D是△ABC的边AB的中点,BD=CE,CE∥AB,AC与DE相交于F.试说明DF与EF的关系.
解:DF=EF
因为D是AB的中点,所以AD=BD,
又因为BD=CE,所以AD=CE,
因为CE∥AD,所以∠A=∠ECF,∠ADF=∠E,
因为BD=CE,
所以△ADF≌△CEF(ASA).
所以DF=EF.
D
B
A
C
F
E
如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF;试判断△ABC和△DEF是否全等.
A
B
C
D
E
F
根据三角形内角和等于180°.
不难发现,∠C=∠F.
那么,在△ABC和△DEF中,
∠B=∠E
BC=EF
∠C=∠F
所以△ABC ≌△DEF(ASA).
(二)两个角及其中一角的对边
通过上述的探究过程我们可以得出以下结论,
也就是说,三角形两个角的大小和其中一个角的对边的长度确定了,
那么这个三角形大小、形状就确定了.
两角和其中一个角的对边分别相等的两个三角形全等.
(可以简写为“角角边”或“AAS”)
符号语言:
在△ABC和△DEF中,
所以△ABC≌△DEF(AAS).
∠A=∠D
∠B=∠E
BC=EF
A
B
C
D
E
F
例2.如图AC,BD相交于点O,∠A=∠D,AB=CD,试说明:△AOB≌△DOC.
解:
分析:根据对顶角相等可得∠AOB=∠DOC,利用“角角边”说明即可.
∠A=∠D
∠AOB=∠DOC
AB=DC
所以△A0B≌△DOC(AAS).
在△AOB和△DOC中,
O
B
C
D
A
2.已知,如图,AB=AE,AB∥DE,∠ECB=70°,∠D=110°,试说明AC与ED的关系.
解:由∠ECB=70°得∠ACB=110°,
又因为∠D=110°,所以∠ACB=∠D.
因为AB∥DE, 所以∠CAB=∠E.
∠ACB=∠D
∠CAB=∠E
AB=EA
在△BCA和△ADE中,
所以△BCA≌△ADE(AAS),
所以AC=ED.
C
A
B
D
E
1.两角和它们的夹边对应相等的两个三角形全等.
2.两角和其中一角的对边对应相等的两个三角形全等.
3.证明三角形全等是说明线段相等(对应边相等),
角相等(对应角相等)等问题的基本途径.
(可以简写为“角角边”或“AAS”)
(可以简写为“角边角”或“ASA”)
第一章 全等三角形
1.2 怎样判定三角形全等
第2课时
1.掌握判定三角形全等的方式——角边角、角角边
2.会通过三角形全等来说明线段相等或角相等
本节课探究一个三角形的两个角和一条边的情形,存在以下两种情况.
如图1,两个角和它们的夹边.
如图2,两个角及其中一角的对边.
A
B
C
图1
A
B
C
图2
(一)两个角和它们的夹边
先任意画一个△ABC,再画一个△DEF.使EF=BC,∠E=∠B,∠F=∠C.把画好的△DEF剪下来,放到△ABC上,判断它们是否全等.
画法如下:
A
B
C
1.画EF=BC;
2. 在EF同一侧画∠MEF=∠B,∠NFE=∠C;
EM和FN相交于D点.
D
E
F
结论:△ABC≌△DEF.
M
N
通过探究过程我们就可以得出以下结论,用它可以判定两个三角形全等.
也就是说,三角形两个角的大小和它们夹边的长度确定了,
那么这个三角形大小、形状就确定了.
两角和它们的夹边分别相等的两个三角形全等.
(可以简写为“角边角”或“ASA”)
角边角定理
符号语言:
在△ABC和△DEF中,
所以 △ABC ≌△DEF(ASA).
∠B=∠E
BC=EF
∠C=∠F
A
B
C
D
E
F
例1.如图,GC=GE,BE=FC,∠B=∠F.试说明:△ABC≌△DFE.
解:因为GC=GE,所以∠ACB=∠DEF,
因为BE=FC,所以BC=FE,
分析:求出BC=EF,∠DEF=∠ACB,根据判定定理ASA说明即可.
∠B=∠F
BC=FE
∠ACB=∠DEF
所以△ABC≌△DFE(ASA).
在△ABC和△DFE中,
A
B
C
G
E
D
F
1.如图,D是△ABC的边AB的中点,BD=CE,CE∥AB,AC与DE相交于F.试说明DF与EF的关系.
解:DF=EF
因为D是AB的中点,所以AD=BD,
又因为BD=CE,所以AD=CE,
因为CE∥AD,所以∠A=∠ECF,∠ADF=∠E,
因为BD=CE,
所以△ADF≌△CEF(ASA).
所以DF=EF.
D
B
A
C
F
E
如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF;试判断△ABC和△DEF是否全等.
A
B
C
D
E
F
根据三角形内角和等于180°.
不难发现,∠C=∠F.
那么,在△ABC和△DEF中,
∠B=∠E
BC=EF
∠C=∠F
所以△ABC ≌△DEF(ASA).
(二)两个角及其中一角的对边
通过上述的探究过程我们可以得出以下结论,
也就是说,三角形两个角的大小和其中一个角的对边的长度确定了,
那么这个三角形大小、形状就确定了.
两角和其中一个角的对边分别相等的两个三角形全等.
(可以简写为“角角边”或“AAS”)
符号语言:
在△ABC和△DEF中,
所以△ABC≌△DEF(AAS).
∠A=∠D
∠B=∠E
BC=EF
A
B
C
D
E
F
例2.如图AC,BD相交于点O,∠A=∠D,AB=CD,试说明:△AOB≌△DOC.
解:
分析:根据对顶角相等可得∠AOB=∠DOC,利用“角角边”说明即可.
∠A=∠D
∠AOB=∠DOC
AB=DC
所以△A0B≌△DOC(AAS).
在△AOB和△DOC中,
O
B
C
D
A
2.已知,如图,AB=AE,AB∥DE,∠ECB=70°,∠D=110°,试说明AC与ED的关系.
解:由∠ECB=70°得∠ACB=110°,
又因为∠D=110°,所以∠ACB=∠D.
因为AB∥DE, 所以∠CAB=∠E.
∠ACB=∠D
∠CAB=∠E
AB=EA
在△BCA和△ADE中,
所以△BCA≌△ADE(AAS),
所以AC=ED.
C
A
B
D
E
1.两角和它们的夹边对应相等的两个三角形全等.
2.两角和其中一角的对边对应相等的两个三角形全等.
3.证明三角形全等是说明线段相等(对应边相等),
角相等(对应角相等)等问题的基本途径.
(可以简写为“角角边”或“AAS”)
(可以简写为“角边角”或“ASA”)
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
