青岛版八年级上册数学1.2 怎样判定三角形全等 第3课时 课件(共16张PPT)
文档属性
| 名称 | 青岛版八年级上册数学1.2 怎样判定三角形全等 第3课时 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 914.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 17:38:30 | ||
图片预览



文档简介
(共16张PPT)
第3课时
第一章 全等三角形
1.2 怎样判定三角形全等
1.探究判定三角形全等的方式——边边边(重点)
2.知道三角形具有稳定性
3.能知道两边分别相等且其中一组等边的对角相等的两个三角形不一定全等
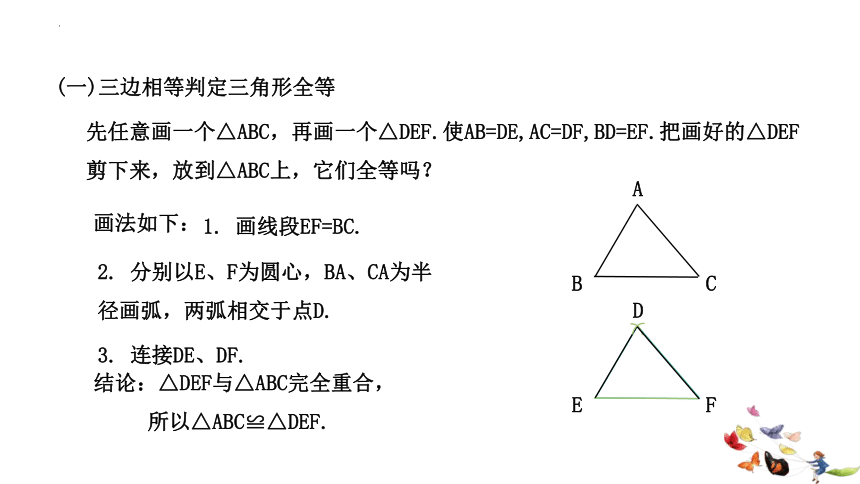
先任意画一个△ABC,再画一个△DEF.使AB=DE,AC=DF,BD=EF.把画好的△DEF剪下来,放到△ABC上,它们全等吗?
画法如下:
A
B
C
1. 画线段EF=BC.
2. 分别以E、F为圆心,BA、CA为半
径画弧,两弧相交于点D.
3. 连接DE、DF.
D
E
F
结论:△DEF与△ABC完全重合,
所以△ABC≌△DEF.
(一)三边相等判定三角形全等
A
B
C
D
E
F
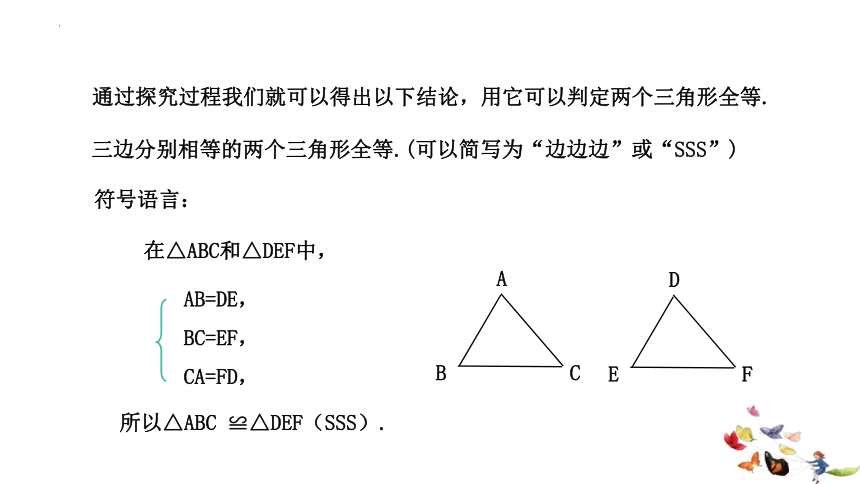
符号语言:
在△ABC和△DEF中,
所以△ABC ≌△DEF(SSS).
AB=DE,
BC=EF,
CA=FD,
通过探究过程我们就可以得出以下结论,用它可以判定两个三角形全等.
三边分别相等的两个三角形全等.(可以简写为“边边边”或“SSS”)
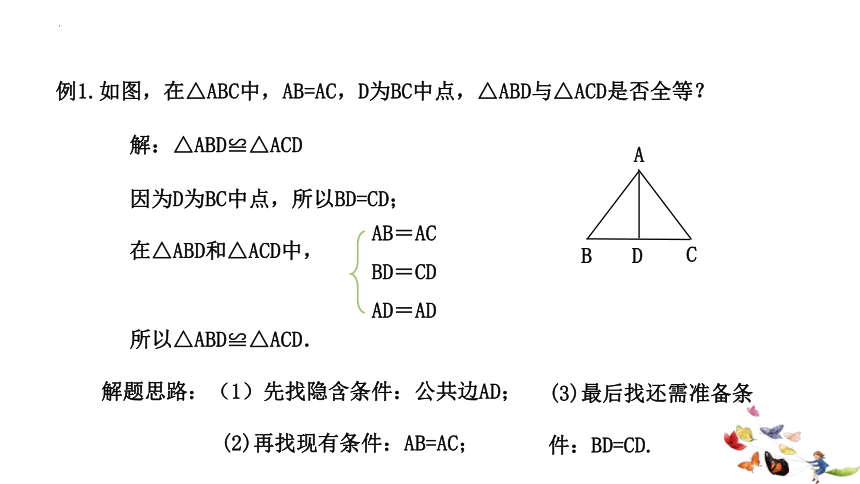
例1.如图,在△ABC中,AB=AC,D为BC中点,△ABD与△ACD是否全等?
因为D为BC中点,所以BD=CD;
在△ABD和△ACD中,
A
B
C
D
AB=AC
BD=CD
AD=AD
所以△ABD≌△ACD.
解题思路:(1)先找隐含条件:公共边AD;
(2)再找现有条件:AB=AC;
(3)最后找还需准备条件:BD=CD.
解:△ABD≌△ACD
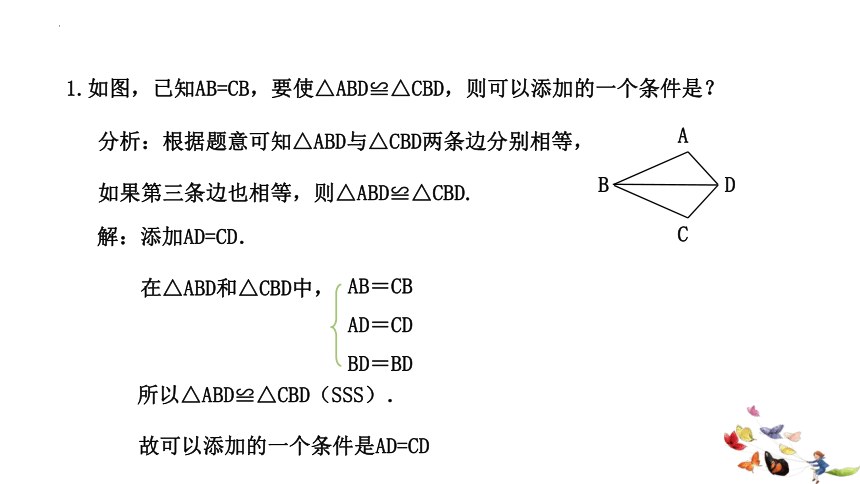
AB=CB
AD=CD
BD=BD
分析:根据题意可知△ABD与△CBD两条边分别相等,如果第三条边也相等,则△ABD≌△CBD.
解:添加AD=CD.
在△ABD和△CBD中,
所以△ABD≌△CBD(SSS).
故可以添加的一个条件是AD=CD
A
B
D
C
1.如图,已知AB=CB,要使△ABD≌△CBD,则可以添加的一个条件是?
试一试:盖房子时,在窗框安装好之前,木工师傅常常先在窗框上斜钉
一根木条,为什么要这样做呢?我们来进行下面的操作.
(1)如图,将三根木条用钉子钉成一个三角形木架,然后扭动它,它的
形状会改变吗?
形状不会改变
(二)三角形的稳定性
(2)如图,将四根木条用钉子钉成一个四边形木架,然后扭动它,它的
形状会改变吗?
形状会发生改变
(3)如图,如图,在四边形木架上再钉一根木条,将它的一对不相邻的
顶点连接起来,然后再扭动它,这时木架的形状还会改变吗?
这时,形状不会发生改变
思考:通过以上的操作你能得出什么结论?
结论:通过以上操作可以发现,三角形木架的形状不会改变,而四边形木架的形状会改变.这就是说,三角形是具有稳定性的图形,而四边形没有稳定性.
例2.人站在晃动的公共汽车上,若你分开两腿站立,还需伸出一只手抓住
栏杆才能站稳,这是利用了 .
分析:分开站立,再伸出一只手抓住栏杆,这时,两脚以及抓住栏杆的手可看作三个点,这三个点的连线恰好组成一个三角形,而三角形具有稳定性,这样人就能站稳了.
三角形的稳定性
2.如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变
形,这种做法的根据是( )
A.两点之间,线段最短
B.长方形的对称性
C.长方形的四个角都是直角
D.三角形的稳定性
D
3.下列物品中利用四边形不稳定性的是( )
A.活动的四边形衣架 B.自行车车架
C.屋顶三角形钢架 D.起重机
A
1.画出一个和图中三角形模样大致相同的三角形△ABC
2.以A点圆心,AC为半径画圆,交BC于点D.
3.连接AD.
D
A
B
C
在△ABC和△ABD中,AB=AB,AC=AD,∠B=∠B;但△ABC和△ABD不全等.
结论:两边和其中一边的对角相等(边边角)不能判定两个三角形全等.
(三)“两边和其中一边的对角”是否判定三角形全等
例3.下列条件中,不能说明△ABC≌△DEF的是( )
A.AB=DE,∠B=∠E,BC=EF
B.AB=DE,∠A=∠D,AC=DF
C.BC=EF,∠B=∠E,AC=DF
D.BC=EF,∠C=∠F,AC=DF
解析:要判断能不能使△ABC≌△DEF,应看所给出的条件是不是两边和这两边的夹角,只有选项C的条件不符合,故选C.
C
方法总结:判断三角形全等时,注意两边与其中一边的对角相等的两个三角形不一定全等.解题时要根据已知条件的位置来考虑,只具备SSA时是不能判定三角形全等的.
4.如图,把一长一短的两根木棍的一端固定在一起,摆出△ABC.固定住
长木棍,转动短木棍,得到△ABD.这个说明了什么?
A
D
C
B
解:说明了有两边和其中一边的对角分别相等的
两个三角形不一定全等.
三角形全等的“SSS”判定:三边分别相等的两个三角形全等.
三角形具有稳定性,四边形不具有稳定性.
两边和其中一边的对角相等(边边角)不能判定两个三角形全等.
第3课时
第一章 全等三角形
1.2 怎样判定三角形全等
1.探究判定三角形全等的方式——边边边(重点)
2.知道三角形具有稳定性
3.能知道两边分别相等且其中一组等边的对角相等的两个三角形不一定全等
先任意画一个△ABC,再画一个△DEF.使AB=DE,AC=DF,BD=EF.把画好的△DEF剪下来,放到△ABC上,它们全等吗?
画法如下:
A
B
C
1. 画线段EF=BC.
2. 分别以E、F为圆心,BA、CA为半
径画弧,两弧相交于点D.
3. 连接DE、DF.
D
E
F
结论:△DEF与△ABC完全重合,
所以△ABC≌△DEF.
(一)三边相等判定三角形全等
A
B
C
D
E
F
符号语言:
在△ABC和△DEF中,
所以△ABC ≌△DEF(SSS).
AB=DE,
BC=EF,
CA=FD,
通过探究过程我们就可以得出以下结论,用它可以判定两个三角形全等.
三边分别相等的两个三角形全等.(可以简写为“边边边”或“SSS”)
例1.如图,在△ABC中,AB=AC,D为BC中点,△ABD与△ACD是否全等?
因为D为BC中点,所以BD=CD;
在△ABD和△ACD中,
A
B
C
D
AB=AC
BD=CD
AD=AD
所以△ABD≌△ACD.
解题思路:(1)先找隐含条件:公共边AD;
(2)再找现有条件:AB=AC;
(3)最后找还需准备条件:BD=CD.
解:△ABD≌△ACD
AB=CB
AD=CD
BD=BD
分析:根据题意可知△ABD与△CBD两条边分别相等,如果第三条边也相等,则△ABD≌△CBD.
解:添加AD=CD.
在△ABD和△CBD中,
所以△ABD≌△CBD(SSS).
故可以添加的一个条件是AD=CD
A
B
D
C
1.如图,已知AB=CB,要使△ABD≌△CBD,则可以添加的一个条件是?
试一试:盖房子时,在窗框安装好之前,木工师傅常常先在窗框上斜钉
一根木条,为什么要这样做呢?我们来进行下面的操作.
(1)如图,将三根木条用钉子钉成一个三角形木架,然后扭动它,它的
形状会改变吗?
形状不会改变
(二)三角形的稳定性
(2)如图,将四根木条用钉子钉成一个四边形木架,然后扭动它,它的
形状会改变吗?
形状会发生改变
(3)如图,如图,在四边形木架上再钉一根木条,将它的一对不相邻的
顶点连接起来,然后再扭动它,这时木架的形状还会改变吗?
这时,形状不会发生改变
思考:通过以上的操作你能得出什么结论?
结论:通过以上操作可以发现,三角形木架的形状不会改变,而四边形木架的形状会改变.这就是说,三角形是具有稳定性的图形,而四边形没有稳定性.
例2.人站在晃动的公共汽车上,若你分开两腿站立,还需伸出一只手抓住
栏杆才能站稳,这是利用了 .
分析:分开站立,再伸出一只手抓住栏杆,这时,两脚以及抓住栏杆的手可看作三个点,这三个点的连线恰好组成一个三角形,而三角形具有稳定性,这样人就能站稳了.
三角形的稳定性
2.如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变
形,这种做法的根据是( )
A.两点之间,线段最短
B.长方形的对称性
C.长方形的四个角都是直角
D.三角形的稳定性
D
3.下列物品中利用四边形不稳定性的是( )
A.活动的四边形衣架 B.自行车车架
C.屋顶三角形钢架 D.起重机
A
1.画出一个和图中三角形模样大致相同的三角形△ABC
2.以A点圆心,AC为半径画圆,交BC于点D.
3.连接AD.
D
A
B
C
在△ABC和△ABD中,AB=AB,AC=AD,∠B=∠B;但△ABC和△ABD不全等.
结论:两边和其中一边的对角相等(边边角)不能判定两个三角形全等.
(三)“两边和其中一边的对角”是否判定三角形全等
例3.下列条件中,不能说明△ABC≌△DEF的是( )
A.AB=DE,∠B=∠E,BC=EF
B.AB=DE,∠A=∠D,AC=DF
C.BC=EF,∠B=∠E,AC=DF
D.BC=EF,∠C=∠F,AC=DF
解析:要判断能不能使△ABC≌△DEF,应看所给出的条件是不是两边和这两边的夹角,只有选项C的条件不符合,故选C.
C
方法总结:判断三角形全等时,注意两边与其中一边的对角相等的两个三角形不一定全等.解题时要根据已知条件的位置来考虑,只具备SSA时是不能判定三角形全等的.
4.如图,把一长一短的两根木棍的一端固定在一起,摆出△ABC.固定住
长木棍,转动短木棍,得到△ABD.这个说明了什么?
A
D
C
B
解:说明了有两边和其中一边的对角分别相等的
两个三角形不一定全等.
三角形全等的“SSS”判定:三边分别相等的两个三角形全等.
三角形具有稳定性,四边形不具有稳定性.
两边和其中一边的对角相等(边边角)不能判定两个三角形全等.
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
