13.2 多边形 第1课时 课件(共16张PPT) 青岛版七年级数学下册
文档属性
| 名称 | 13.2 多边形 第1课时 课件(共16张PPT) 青岛版七年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 18:40:29 | ||
图片预览





文档简介
(共16张PPT)
第十三章 平面图形的认识
13.2 多边形
第1课时
1.掌握多边形的定义及有关概念,能区分凹凸多边形.
2.掌握正多边形的概念.
3.会求多边形的对角线的条数.
下面的图片中有哪些熟悉的平面图形?
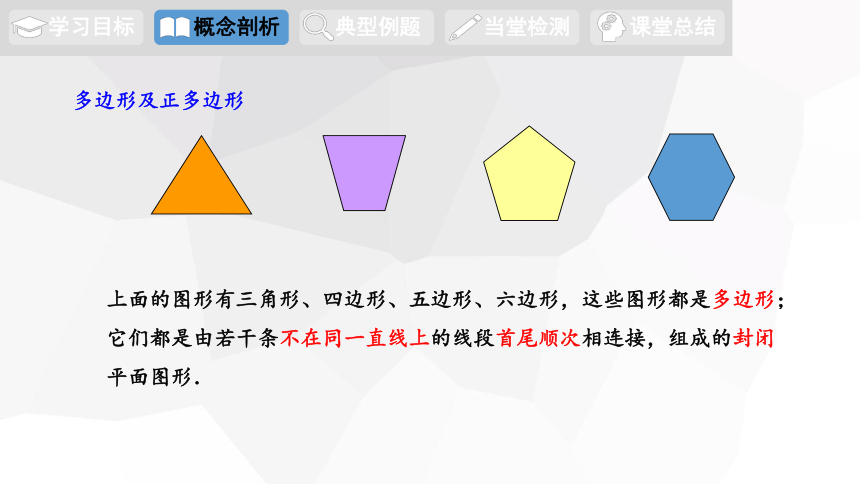
上面的图形有三角形、四边形、五边形、六边形,这些图形都是多边形;
它们都是由若干条不在同一直线上的线段首尾顺次相连接,组成的封闭
平面图形.
多边形及正多边形
组成多边形的各条线段叫做多边形的边.
每相邻两条边的公共端点叫做多边形的顶点.
在多边形中,连接不相邻两个顶点的线段叫做多边形的对角线.
每相邻两条边的形成的夹角叫做多边形的内角.
边
内角
顶点
对角线
提示:我们平常所说的多边形都是指凸多边形,即多边形总在任何一
条边所在直线的同一侧.
凸多边形
凹多边形
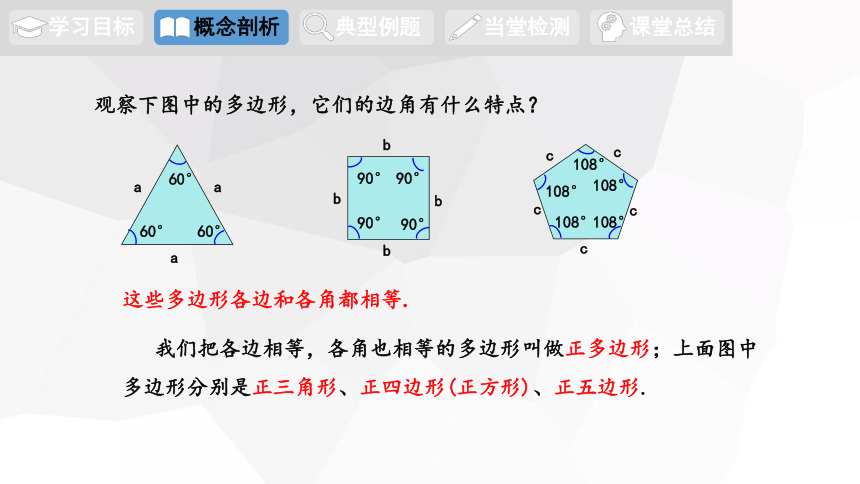
观察下图中的多边形,它们的边角有什么特点?
这些多边形各边和各角都相等.
我们把各边相等,各角也相等的多边形叫做正多边形;上面图中
多边形分别是正三角形、正四边形(正方形)、正五边形.
60°
a
a
a
60°
60°
b
b
b
b
90°
90°
90°
90°
108°
c
c
c
c
c
108°
108°
108°
108°
例1.观察并填空.
(1)数一数:一个四边形有 条对角线;一个五边形有 条对角线;
(2)画一画:一个六边形有____条对角线.
9
5
2
1.下列图形是多边形的有: .(只填序号)
(1)(4)
(1)
(2)
(4)
(3)
(5)
(6)
2.刘师傅把一个四边形的木板锯掉一个角,那么剩下的木板的形
状不可能是( )
A.三角形 B.四边形
C.五边形 D.六边形
D
分析:有三种结果,如图所示:
总结:一个多边形截去一个角后,多边形的边数可能增加了一条,也可
能不变或减少了一条.
问题1:过n边形的每一个顶点有几条对角线?
问题2:n边形一共有多少条对角线?
例2.探索:
任务分配:
1.每人分配一个图形,先过一个顶点画出所有对角线;再在表格中填
出相应的数据;
2.小组交流并汇总完成全部表格.
多边形的边数 4 5 6 7 …… n
从一个顶点出发的对角线的条数 ……
对角线的总条数 ……
1
2
3
4
2
5
9
14
n-3
总结:过n边形的一个顶点可以引入(n-3)条对角线,n边形一共有
条对角线.
3.在六边形的一边上取一点与顶点连接,将六边形分割成三角形的个数为( )
A.3 B.4 C.5 D.6
C
分析:根据题意,分割后图形如右图:
由图可知,六边形被分割成5个三角形,故C选项正确.
4.(1)一个凸十二边形有______条对角线.
(2)若一个多边形对角线的条数恰好为边数的3倍,则这个多边形的边
数为 .
(3)若过m边形的一个顶点有7条对角线,n边形没有对角线,k边形对
角线共有k条,则m+n+k= .
9
18
54
多边形
定义
对角线
正多
边形
n(n≥3)边形共有对角线 条.
第十三章 平面图形的认识
13.2 多边形
第1课时
1.掌握多边形的定义及有关概念,能区分凹凸多边形.
2.掌握正多边形的概念.
3.会求多边形的对角线的条数.
下面的图片中有哪些熟悉的平面图形?
上面的图形有三角形、四边形、五边形、六边形,这些图形都是多边形;
它们都是由若干条不在同一直线上的线段首尾顺次相连接,组成的封闭
平面图形.
多边形及正多边形
组成多边形的各条线段叫做多边形的边.
每相邻两条边的公共端点叫做多边形的顶点.
在多边形中,连接不相邻两个顶点的线段叫做多边形的对角线.
每相邻两条边的形成的夹角叫做多边形的内角.
边
内角
顶点
对角线
提示:我们平常所说的多边形都是指凸多边形,即多边形总在任何一
条边所在直线的同一侧.
凸多边形
凹多边形
观察下图中的多边形,它们的边角有什么特点?
这些多边形各边和各角都相等.
我们把各边相等,各角也相等的多边形叫做正多边形;上面图中
多边形分别是正三角形、正四边形(正方形)、正五边形.
60°
a
a
a
60°
60°
b
b
b
b
90°
90°
90°
90°
108°
c
c
c
c
c
108°
108°
108°
108°
例1.观察并填空.
(1)数一数:一个四边形有 条对角线;一个五边形有 条对角线;
(2)画一画:一个六边形有____条对角线.
9
5
2
1.下列图形是多边形的有: .(只填序号)
(1)(4)
(1)
(2)
(4)
(3)
(5)
(6)
2.刘师傅把一个四边形的木板锯掉一个角,那么剩下的木板的形
状不可能是( )
A.三角形 B.四边形
C.五边形 D.六边形
D
分析:有三种结果,如图所示:
总结:一个多边形截去一个角后,多边形的边数可能增加了一条,也可
能不变或减少了一条.
问题1:过n边形的每一个顶点有几条对角线?
问题2:n边形一共有多少条对角线?
例2.探索:
任务分配:
1.每人分配一个图形,先过一个顶点画出所有对角线;再在表格中填
出相应的数据;
2.小组交流并汇总完成全部表格.
多边形的边数 4 5 6 7 …… n
从一个顶点出发的对角线的条数 ……
对角线的总条数 ……
1
2
3
4
2
5
9
14
n-3
总结:过n边形的一个顶点可以引入(n-3)条对角线,n边形一共有
条对角线.
3.在六边形的一边上取一点与顶点连接,将六边形分割成三角形的个数为( )
A.3 B.4 C.5 D.6
C
分析:根据题意,分割后图形如右图:
由图可知,六边形被分割成5个三角形,故C选项正确.
4.(1)一个凸十二边形有______条对角线.
(2)若一个多边形对角线的条数恰好为边数的3倍,则这个多边形的边
数为 .
(3)若过m边形的一个顶点有7条对角线,n边形没有对角线,k边形对
角线共有k条,则m+n+k= .
9
18
54
多边形
定义
对角线
正多
边形
n(n≥3)边形共有对角线 条.
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
