青岛版七年级下册数学12.2 完全平方公式 第1课时 课件 (共14张PPT)
文档属性
| 名称 | 青岛版七年级下册数学12.2 完全平方公式 第1课时 课件 (共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 359.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 00:00:00 | ||
图片预览





文档简介
(共14张PPT)
第12章 乘法公式与因式分解
12.2 完全平方公式 第1课时
1.会推导完全平方公式,会用几何图形验证公式;(重点)
2.能运用完全平方公式进行简单的计算.(难点)
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
一位老人非常喜欢孩子,每当有孩子到他家做客时,老人都要拿出糖果招待他们.来一个孩子老人就给孩子一块糖;来两个孩子,老人就给每个孩子两块糖…
(1)第一天,来了a个男孩子,老人一共给了a2块糖;
(2)第二天,来了b个女孩子,老人一共给了b2块糖;
(3)第三天,这(a+b)个孩子都来了,老人一共给了(a+b)2个糖.
思考:老人前两天加起来给的糖果多,还是第三天给的糖果多?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
上面的几个运算都是形如(a±b)2的多项式相乘,结果一共有 项,第一项为 ,最后一项为 .
a2
m2-4m+4
3
做一做:计算下列多项式的积,你能发现什么规律?
(1)(p+1)2=(p+1)(p+1) = .
(2)(m+2)2=(m+2)(m+2)= .
(3)(p-1)2=(p-1)(p-1)= .
(4) (m-2)2 =(m-2)(m-2)= .
p2+2p+1
m2+4m+4
p2-2p+1
b2
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(a+b)(a+b)
=a2+ab+ab+b2
=a2+2ab+b2
(a-b)(a-b)
=a2-ab-ab+b2
=a2-2ab+b2
由于(a+b)2=
所以,对于这种形式的多项式相乘,我们可以直接写出运算结果,即
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
(a-b)2=
典型例题
当堂检测
学习目标
课堂总结
概念剖析
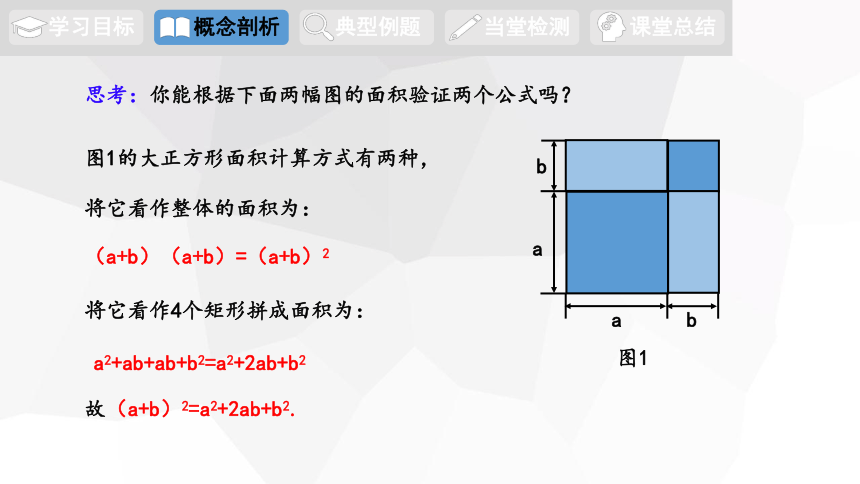
思考:你能根据下面两幅图的面积验证两个公式吗?
a
a
b
b
图1
图1的大正方形面积计算方式有两种,
将它看作整体的面积为:
(a+b)(a+b)=(a+b)2
将它看作4个矩形拼成面积为:
a2+ab+ab+b2=a2+2ab+b2
故(a+b)2=a2+2ab+b2.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
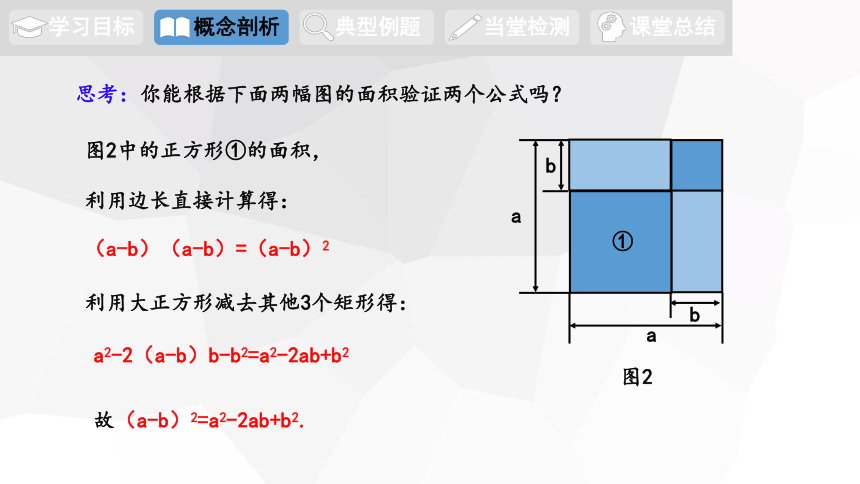
思考:你能根据下面两幅图的面积验证两个公式吗?
a
a
b
b
图2
图2中的正方形①的面积,
利用边长直接计算得:
(a-b)(a-b)=(a-b)2
利用大正方形减去其他3个矩形得:
故(a-b)2=a2-2ab+b2.
①
a2-2(a-b)b-b2=a2-2ab+b2
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2
上面两个公式今后可以直接应用于计算,称为完全平方公式.
文字叙述:两数和(差)的平方,等于它们的平方和,加上(减去)它们的积的2倍.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
解:(1)原式=
归纳:先和公式对照,分清楚a和b,公式中2ab前面的2不要遗漏.
(2)原式=
y2-2·y· +( )2
=y2-y+ .
例1.利用完全平方公式计算.
(1)(4m+n)2 ; (2)(y- )2
分析:对比公式,分清a和b,直接套用公式即可.
(1)式可套用公式(a+b)2=a2+2ab+b2,这里a是4m,b是n;
(2)式可套用公式(a-b)2=a2-2ab+b2,这里a是y,b是 .
(4m)2 +2×4m·n+n2
=16m2+8mn+n2;
典型例题
当堂检测
学习目标
课堂总结
概念剖析
解:(1)计算结果有三项,这里很明显漏项了.
改正:(a+b)2=a2+2ab+b2
1.下面各式的计算错在哪里?应当怎样改正.
(1)(a+b)2=a2+b2; (2)(a-b)2=a2-ab+b2;
(3)(a-2)2=a2+4a+4.
(2)对比公式发现结果中“-ab”错误.
改正:(a-b)2=a2-2ab+b2.
(3)这里混淆了两种公式(a+b)2和(a-b)2的结果.
改正:(a-2)2=a2-4a+4.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.利用完全平方公式计算:
(1)(x+3)2 ;(2)(2x-5)2 ;(3) .
解:(1)原式=x2+2·x·3+32=x2+6x+9;
(2)原式=(2x)2-2×(2x)×5+52=4x2-20x+25;
(3)原式=
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例2.利用完全平方公式计算:
(1)1022 ; (2)992 .
分析:为方便计算,这里的102可看作100+2,99可看作100-1.
解:
(1)原式=(100+2)2
=1002+2×100×2+22
=10000+400+4
=10404;
(2)原式=(100-1)2
=1002-2×100×1+12
=10000-200+1
=9801.
【当堂检】
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3.利用平方差公式计算:
(1)512; (2)982.
解:(1)原式=(50+1)2
=2500+100+1
=2601;
(2)原式=(100-2)2
=10000-400+4
=9604.
文字描述:
典型例题
当堂检测
学习目标
课堂总结
概念剖析
符号描述:
完全平方公式
(a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2
两数和(差)的平方,等于它们的平方和,加上(减去)它们的积的2倍.
第12章 乘法公式与因式分解
12.2 完全平方公式 第1课时
1.会推导完全平方公式,会用几何图形验证公式;(重点)
2.能运用完全平方公式进行简单的计算.(难点)
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
一位老人非常喜欢孩子,每当有孩子到他家做客时,老人都要拿出糖果招待他们.来一个孩子老人就给孩子一块糖;来两个孩子,老人就给每个孩子两块糖…
(1)第一天,来了a个男孩子,老人一共给了a2块糖;
(2)第二天,来了b个女孩子,老人一共给了b2块糖;
(3)第三天,这(a+b)个孩子都来了,老人一共给了(a+b)2个糖.
思考:老人前两天加起来给的糖果多,还是第三天给的糖果多?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
上面的几个运算都是形如(a±b)2的多项式相乘,结果一共有 项,第一项为 ,最后一项为 .
a2
m2-4m+4
3
做一做:计算下列多项式的积,你能发现什么规律?
(1)(p+1)2=(p+1)(p+1) = .
(2)(m+2)2=(m+2)(m+2)= .
(3)(p-1)2=(p-1)(p-1)= .
(4) (m-2)2 =(m-2)(m-2)= .
p2+2p+1
m2+4m+4
p2-2p+1
b2
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(a+b)(a+b)
=a2+ab+ab+b2
=a2+2ab+b2
(a-b)(a-b)
=a2-ab-ab+b2
=a2-2ab+b2
由于(a+b)2=
所以,对于这种形式的多项式相乘,我们可以直接写出运算结果,即
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
(a-b)2=
典型例题
当堂检测
学习目标
课堂总结
概念剖析
思考:你能根据下面两幅图的面积验证两个公式吗?
a
a
b
b
图1
图1的大正方形面积计算方式有两种,
将它看作整体的面积为:
(a+b)(a+b)=(a+b)2
将它看作4个矩形拼成面积为:
a2+ab+ab+b2=a2+2ab+b2
故(a+b)2=a2+2ab+b2.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
思考:你能根据下面两幅图的面积验证两个公式吗?
a
a
b
b
图2
图2中的正方形①的面积,
利用边长直接计算得:
(a-b)(a-b)=(a-b)2
利用大正方形减去其他3个矩形得:
故(a-b)2=a2-2ab+b2.
①
a2-2(a-b)b-b2=a2-2ab+b2
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2
上面两个公式今后可以直接应用于计算,称为完全平方公式.
文字叙述:两数和(差)的平方,等于它们的平方和,加上(减去)它们的积的2倍.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
解:(1)原式=
归纳:先和公式对照,分清楚a和b,公式中2ab前面的2不要遗漏.
(2)原式=
y2-2·y· +( )2
=y2-y+ .
例1.利用完全平方公式计算.
(1)(4m+n)2 ; (2)(y- )2
分析:对比公式,分清a和b,直接套用公式即可.
(1)式可套用公式(a+b)2=a2+2ab+b2,这里a是4m,b是n;
(2)式可套用公式(a-b)2=a2-2ab+b2,这里a是y,b是 .
(4m)2 +2×4m·n+n2
=16m2+8mn+n2;
典型例题
当堂检测
学习目标
课堂总结
概念剖析
解:(1)计算结果有三项,这里很明显漏项了.
改正:(a+b)2=a2+2ab+b2
1.下面各式的计算错在哪里?应当怎样改正.
(1)(a+b)2=a2+b2; (2)(a-b)2=a2-ab+b2;
(3)(a-2)2=a2+4a+4.
(2)对比公式发现结果中“-ab”错误.
改正:(a-b)2=a2-2ab+b2.
(3)这里混淆了两种公式(a+b)2和(a-b)2的结果.
改正:(a-2)2=a2-4a+4.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.利用完全平方公式计算:
(1)(x+3)2 ;(2)(2x-5)2 ;(3) .
解:(1)原式=x2+2·x·3+32=x2+6x+9;
(2)原式=(2x)2-2×(2x)×5+52=4x2-20x+25;
(3)原式=
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例2.利用完全平方公式计算:
(1)1022 ; (2)992 .
分析:为方便计算,这里的102可看作100+2,99可看作100-1.
解:
(1)原式=(100+2)2
=1002+2×100×2+22
=10000+400+4
=10404;
(2)原式=(100-1)2
=1002-2×100×1+12
=10000-200+1
=9801.
【当堂检】
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3.利用平方差公式计算:
(1)512; (2)982.
解:(1)原式=(50+1)2
=2500+100+1
=2601;
(2)原式=(100-2)2
=10000-400+4
=9604.
文字描述:
典型例题
当堂检测
学习目标
课堂总结
概念剖析
符号描述:
完全平方公式
(a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2
两数和(差)的平方,等于它们的平方和,加上(减去)它们的积的2倍.
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
