青岛版七年级下册数学11.3 单项式的乘法 第2课时 课件(共14张PPT)
文档属性
| 名称 | 青岛版七年级下册数学11.3 单项式的乘法 第2课时 课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 202.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
第十一章 整式的乘除
第2课时
11.3 单项式的乘法
1.能推导及掌握单项式乘以多项式法则;
2.能进行单项式与多项式相乘的相关运算.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
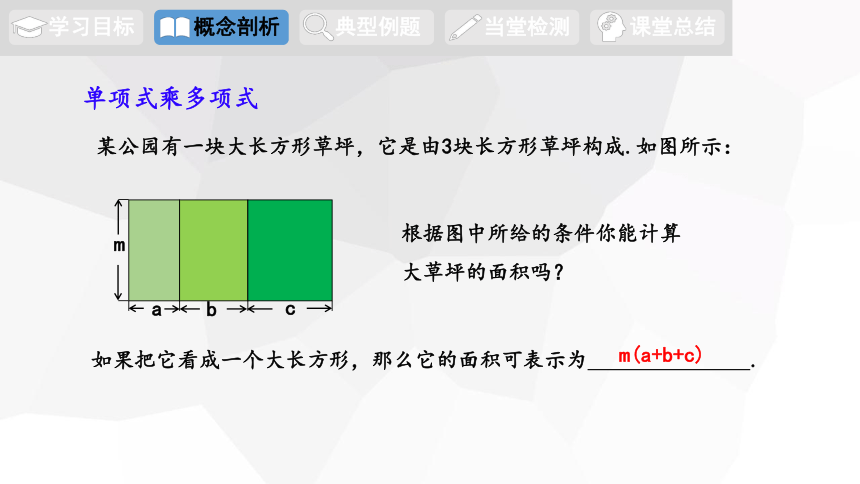
某公园有一块大长方形草坪,它是由3块长方形草坪构成.如图所示:
单项式乘多项式
a
c
b
m
根据图中所给的条件你能计算
大草坪的面积吗?
如果把它看成一个大长方形,那么它的面积可表示为 .
m(a+b+c)
典型例题
当堂检测
学习目标
课堂总结
概念剖析
a
c
b
m
还可以把它看成三个小长方形,小长方形的面积可分别表示为 、
、 ;大草坪的面积为 .
思考:还有其它方法计算吗?
=
ma+mb+mc
ma
mb
mc
ma+mb+mc
m(a+b+c)
计算1
计算2
典型例题
当堂检测
学习目标
课堂总结
概念剖析
m(a+b+c)=ma+mb+mc
利用乘法分配律也能得出这个等式
类似地单项式3a2与多项式a3-4b+c相乘,
3a2(a3-4b+c)=
3a2·a3 + [3a2·(-4b)] + 3a2·c
这些式子是什么形式?
单项式乘单项式
典型例题
当堂检测
学习目标
课堂总结
概念剖析
单项式与多项式相乘,就是用单项式去乘多项式的每一项,转化成单项式乘单项式,再把所得的积相加.
单项式与多项式相乘的法则:
归纳:
2c5 2b2+ 2c5 3c2
例如2c5(2b2+3c2)
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例1.计算.
(1)(-4x2)(3x+1) (2)(0.5ab2-2ab)·2ab
解:(1)原式=(-4x2)(3x)+(-4x2)
=(-4×3)(x2·x)+(-4x2)
=-12x3-4x2
(2)原式=0.5ab2·2ab+(-2ab)·2ab
=a2b3-4a2b2
典型例题
当堂检测
学习目标
课堂总结
概念剖析
注意:
1.单项式乘多项式的结果是多项式,积的项数与原多项式的
项数相同.
3.不要出现漏乘现象,运算要有顺序.
2.单项式分别与多项式的每一项相乘时,要注意积的符号的确定.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.计算.
(1)3a(5a-2b) (2)(x-3y)(-6x)
(3)2a2(2ab+3a4) (4)2(x2)3(y2+x2y)
解:(1)原式=3a·5a+3a(-2b)
=15a2-6ab
(2)原式=x(-6x)+(-3y)(-6x)
=-6x2+18xy
(3)原式=2a2·2ab+2a2·3a4
=4a3b+6a6
(4)原式=2x6(y2+x2y)
=2x6·y2+2x6·x2y
=2x6y2+2x8y
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例2.已知 ab2=-6,求-ab(a2b5-ab3-b).
解:原式=-a3b6+a2b4+ab2
当ab2=-6时,原式=-(-6)3 +(-6)2 -6=246
=-(ab2)3 +(ab2)2+ab2
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例3.一个长方体的长为3x+1,宽为2x,高为3x,求它的表面积.
【分析】接利用长方体表面积求法以及结合单项式乘以单项式以及单项式乘以多项式运算法则分别计算得出即可.
解:因为一个长方体的长为3x+1,宽为2x,高为3x,
所以它的表面积为:2(3x+1) 2x+2 2x 3x+2 3x (3x+1)
=12x2+4x+12x2+18x2+6x
=42x2+10x,
答:此长方体的表面积为42x2+10x.
单项式与多项式相乘的结果中,
应将同类项合并.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.通过计算几何图形的面积可表示一些代数恒等式,如图可表示的代数恒等式是( )
A.(a-b)2=a2-2ab+b2 B.(a+b)2=a2+2ab+b2
C.2a(a+b)=2a2+2ab D.(a+b)(a-b)=a2-b2
C
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3.(1)计算:-2a2·(ab+b2)-5a(a2b-ab2);
(2)化简求值:x(x-1)+2x(x+1)-3x(x-2),其中x=2.
解:(1)原式= -2a3b-2a2b2-5a3b+5a2b2
=(-2a3b-5a3b)+(-2a2b2+5a2b2)
= -7a3b+3a2b2
(2)原式=x2-x+2x2+2x-3x2+6x
当x=2时,原式=14.
=7x
典型例题
当堂检测
学习目标
课堂总结
概念剖析
实质是把单项式乘以多项式转化为单项式乘以单项式.
单项式与多项式相乘的法则:
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把
所得的积相加.
第十一章 整式的乘除
第2课时
11.3 单项式的乘法
1.能推导及掌握单项式乘以多项式法则;
2.能进行单项式与多项式相乘的相关运算.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
某公园有一块大长方形草坪,它是由3块长方形草坪构成.如图所示:
单项式乘多项式
a
c
b
m
根据图中所给的条件你能计算
大草坪的面积吗?
如果把它看成一个大长方形,那么它的面积可表示为 .
m(a+b+c)
典型例题
当堂检测
学习目标
课堂总结
概念剖析
a
c
b
m
还可以把它看成三个小长方形,小长方形的面积可分别表示为 、
、 ;大草坪的面积为 .
思考:还有其它方法计算吗?
=
ma+mb+mc
ma
mb
mc
ma+mb+mc
m(a+b+c)
计算1
计算2
典型例题
当堂检测
学习目标
课堂总结
概念剖析
m(a+b+c)=ma+mb+mc
利用乘法分配律也能得出这个等式
类似地单项式3a2与多项式a3-4b+c相乘,
3a2(a3-4b+c)=
3a2·a3 + [3a2·(-4b)] + 3a2·c
这些式子是什么形式?
单项式乘单项式
典型例题
当堂检测
学习目标
课堂总结
概念剖析
单项式与多项式相乘,就是用单项式去乘多项式的每一项,转化成单项式乘单项式,再把所得的积相加.
单项式与多项式相乘的法则:
归纳:
2c5 2b2+ 2c5 3c2
例如2c5(2b2+3c2)
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例1.计算.
(1)(-4x2)(3x+1) (2)(0.5ab2-2ab)·2ab
解:(1)原式=(-4x2)(3x)+(-4x2)
=(-4×3)(x2·x)+(-4x2)
=-12x3-4x2
(2)原式=0.5ab2·2ab+(-2ab)·2ab
=a2b3-4a2b2
典型例题
当堂检测
学习目标
课堂总结
概念剖析
注意:
1.单项式乘多项式的结果是多项式,积的项数与原多项式的
项数相同.
3.不要出现漏乘现象,运算要有顺序.
2.单项式分别与多项式的每一项相乘时,要注意积的符号的确定.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.计算.
(1)3a(5a-2b) (2)(x-3y)(-6x)
(3)2a2(2ab+3a4) (4)2(x2)3(y2+x2y)
解:(1)原式=3a·5a+3a(-2b)
=15a2-6ab
(2)原式=x(-6x)+(-3y)(-6x)
=-6x2+18xy
(3)原式=2a2·2ab+2a2·3a4
=4a3b+6a6
(4)原式=2x6(y2+x2y)
=2x6·y2+2x6·x2y
=2x6y2+2x8y
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例2.已知 ab2=-6,求-ab(a2b5-ab3-b).
解:原式=-a3b6+a2b4+ab2
当ab2=-6时,原式=-(-6)3 +(-6)2 -6=246
=-(ab2)3 +(ab2)2+ab2
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例3.一个长方体的长为3x+1,宽为2x,高为3x,求它的表面积.
【分析】接利用长方体表面积求法以及结合单项式乘以单项式以及单项式乘以多项式运算法则分别计算得出即可.
解:因为一个长方体的长为3x+1,宽为2x,高为3x,
所以它的表面积为:2(3x+1) 2x+2 2x 3x+2 3x (3x+1)
=12x2+4x+12x2+18x2+6x
=42x2+10x,
答:此长方体的表面积为42x2+10x.
单项式与多项式相乘的结果中,
应将同类项合并.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.通过计算几何图形的面积可表示一些代数恒等式,如图可表示的代数恒等式是( )
A.(a-b)2=a2-2ab+b2 B.(a+b)2=a2+2ab+b2
C.2a(a+b)=2a2+2ab D.(a+b)(a-b)=a2-b2
C
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3.(1)计算:-2a2·(ab+b2)-5a(a2b-ab2);
(2)化简求值:x(x-1)+2x(x+1)-3x(x-2),其中x=2.
解:(1)原式= -2a3b-2a2b2-5a3b+5a2b2
=(-2a3b-5a3b)+(-2a2b2+5a2b2)
= -7a3b+3a2b2
(2)原式=x2-x+2x2+2x-3x2+6x
当x=2时,原式=14.
=7x
典型例题
当堂检测
学习目标
课堂总结
概念剖析
实质是把单项式乘以多项式转化为单项式乘以单项式.
单项式与多项式相乘的法则:
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把
所得的积相加.
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
