人教版数学七年级上册 2.2 整式的加减1 课件 (共15张PPT)
文档属性
| 名称 | 人教版数学七年级上册 2.2 整式的加减1 课件 (共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 32.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 19:43:30 | ||
图片预览






文档简介
(共15张PPT)
2.2 整式的加减
合并同类项
观察超市货物的摆放
情境引入
观察书店书籍的摆放
情境引入
情境引入
如果有一罐硬币(分别有一角,五角,一元), 你会如何去数?
把相同的分别放在一起 再去数!
情境引入
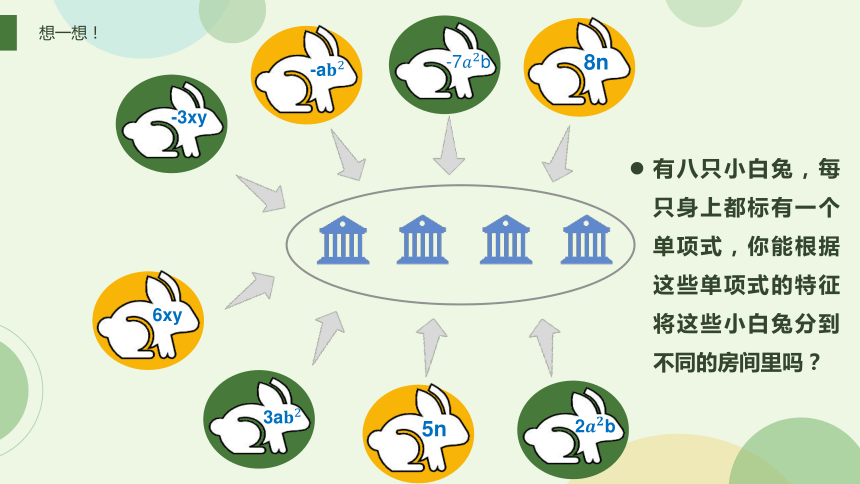
想一想!
有八只小白兔,每只身上都标有一个单项式,你能根据这些单项式的特征将这些小白兔分到不同的房间里吗?
8n
-7b
-a
-3xy
6xy
3a
5n
2b
所含字母相同
知识要点
(4)-7b与2b
(3)3a与-a
(1)5n与8n
(2)6xy与-3xy
2.相同字母指数也相同
我们把具有以上两个特征的单项式称为同类项。
注:所有的常数项也看作同类项
8n 6xy 3a -7b -a -3xy 5n 2b
总结归纳
同类项只与字母及其指数有关,与系数无关,与字母在单项式中的排列顺序无关;
一:
抓住“两个相同”:一是所含字母要完全相同,二是相同字母的指数要相同,这两个条件缺一不可。
二:
不要忘记几个单独的数也是同类型。
三:
同类项的判别
典例精析
例1
(2)在 6y -3 -4y -5y 中没有同类项的项是( )。
6
( 1 ) 判断 5a 与8a是否为同类项( )
是
合并同类项及应用
小明一家要外出游玩,爸爸、妈妈和小明各选他们要吃的东西:
小明买的时候,应该怎样说?
数量
4
3
8
3
(4)个面包 (3)个苹果
(8)颗糖 (3)瓶饮料
奇妙替换
2
+
3
=
5
3
-
2
=
1
y
y
y
你还有其他方法解释吗?
利用乘法分配律可得:
2+3=
(2+3)
=5
3y- 2y=
(3-2)y
=y
替换成
替换成y
知识要点
(1)把多项式中的同类项合并成一项叫做合并同类项。
(2)合并同类项法则:
同类项的系数相加,所得结果作为系数。
字母和字母的指数不变。
3y + 2y= 5y
相加
不变
实际应用
例2
(1)6+2-3++1
=(6-3)+(2+)+1
=(6-3) +(2+1)+1
=3+3+1
(2)如果 2 与 是同类项,则m=( ),n=( )。
2
2
一 找,找出多项式中的同类项,
1
二 移,利用加法交换律,将同类项移动 到同一个括号中。
2
三 并,将同一括号内的同类项相加(系数相加 字母及其指数不变)。
3
小结
感谢观看
THANK YOU
2023.10.25
2.2 整式的加减
合并同类项
观察超市货物的摆放
情境引入
观察书店书籍的摆放
情境引入
情境引入
如果有一罐硬币(分别有一角,五角,一元), 你会如何去数?
把相同的分别放在一起 再去数!
情境引入
想一想!
有八只小白兔,每只身上都标有一个单项式,你能根据这些单项式的特征将这些小白兔分到不同的房间里吗?
8n
-7b
-a
-3xy
6xy
3a
5n
2b
所含字母相同
知识要点
(4)-7b与2b
(3)3a与-a
(1)5n与8n
(2)6xy与-3xy
2.相同字母指数也相同
我们把具有以上两个特征的单项式称为同类项。
注:所有的常数项也看作同类项
8n 6xy 3a -7b -a -3xy 5n 2b
总结归纳
同类项只与字母及其指数有关,与系数无关,与字母在单项式中的排列顺序无关;
一:
抓住“两个相同”:一是所含字母要完全相同,二是相同字母的指数要相同,这两个条件缺一不可。
二:
不要忘记几个单独的数也是同类型。
三:
同类项的判别
典例精析
例1
(2)在 6y -3 -4y -5y 中没有同类项的项是( )。
6
( 1 ) 判断 5a 与8a是否为同类项( )
是
合并同类项及应用
小明一家要外出游玩,爸爸、妈妈和小明各选他们要吃的东西:
小明买的时候,应该怎样说?
数量
4
3
8
3
(4)个面包 (3)个苹果
(8)颗糖 (3)瓶饮料
奇妙替换
2
+
3
=
5
3
-
2
=
1
y
y
y
你还有其他方法解释吗?
利用乘法分配律可得:
2+3=
(2+3)
=5
3y- 2y=
(3-2)y
=y
替换成
替换成y
知识要点
(1)把多项式中的同类项合并成一项叫做合并同类项。
(2)合并同类项法则:
同类项的系数相加,所得结果作为系数。
字母和字母的指数不变。
3y + 2y= 5y
相加
不变
实际应用
例2
(1)6+2-3++1
=(6-3)+(2+)+1
=(6-3) +(2+1)+1
=3+3+1
(2)如果 2 与 是同类项,则m=( ),n=( )。
2
2
一 找,找出多项式中的同类项,
1
二 移,利用加法交换律,将同类项移动 到同一个括号中。
2
三 并,将同一括号内的同类项相加(系数相加 字母及其指数不变)。
3
小结
感谢观看
THANK YOU
2023.10.25
