数学人教A版(2019)必修第一册5.2.1三角函数的概念(共23张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册5.2.1三角函数的概念(共23张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 18:40:23 | ||
图片预览







文档简介
(共23张PPT)
5.2 三角函数的概念
第五章 三角函数
5.2.1 三角函数的概念
探索新知
停顿
问题1 如何研究具体的函数类型,我们研究对数函数的路径是什么
背景
概念
图象和性质
应用
回顾:在初中我们是如何定义锐角三角函数的?
A
C
B
在Rt△ABC中,
它们是以锐角为自变量,边的比值为函数值的三角函数.
对边
邻边
斜边
特殊角的三角函数值
探索新知
上述定义只限于直角三角形中的锐角,而现在角的定义已经拓广到任意角,如:
停顿
师生互动,探索新知
问题2 如图:圆O上的点P以A为起点做逆时针方向旋转。如何借助角α的大小变化刻画点P的位置变化呢?
先研究单位圆上点P的变化情况。
﹒
探索新知
一般地,任意给定一个角 ∈R,它的终边OP与单位圆交点P的坐标,无论是横坐标x还是纵坐标y,都是唯一确定的.
所以,点P的横坐标x、纵坐标y都是角 的函数.
以原点O为圆心,以单位长度(r=1)为半径的圆称为单位圆。
y
o
x
1
M
探索新知
探索新知
任意角三角函数的定义
注意:正弦,余弦,正切都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数,我们将他们称为三角函数.
设 是一个任意角, ∈R ,它的终边OP与单位圆相交于点P(x,y).
(1)把点P的纵坐标y叫做 的正弦函数,记作sin , 即y=sin ;
(2)把点P的横坐标x叫做 的余弦函数,记作cos ,即x= cos ;
(3)把点P的纵坐标与横坐标的比值叫做 的正切,记作tan ,即=tan (x≠0).
﹒
我们将正弦函数、余弦函数和正切函数统称为三角函数,通常将它们记为:
正弦函数
余弦函数
正切函数
点P的纵坐标和横坐标的比值为函数值α的函数,称为正切函数.
思考:其中也是关于α的函数吗?为什么? α也可以取全体实数吗?
探索新知
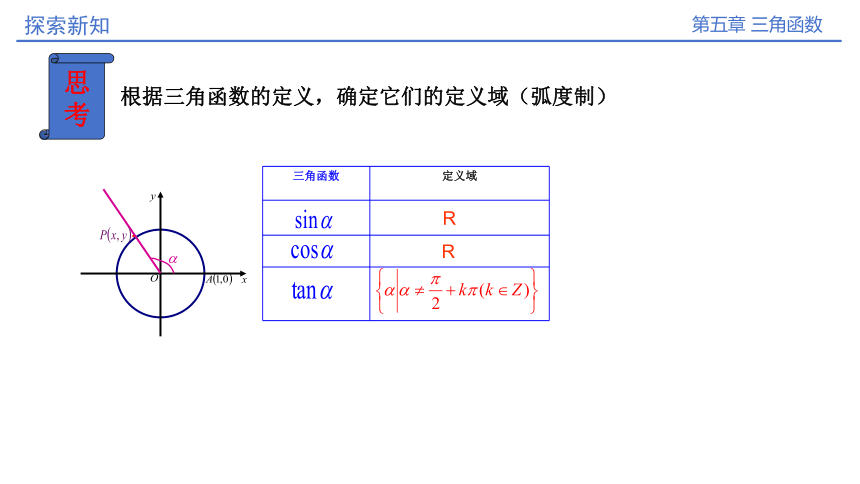
根据三角函数的定义,确定它们的定义域(弧度制)
思
考
三角函数 定义域
R
R
﹒
探索新知
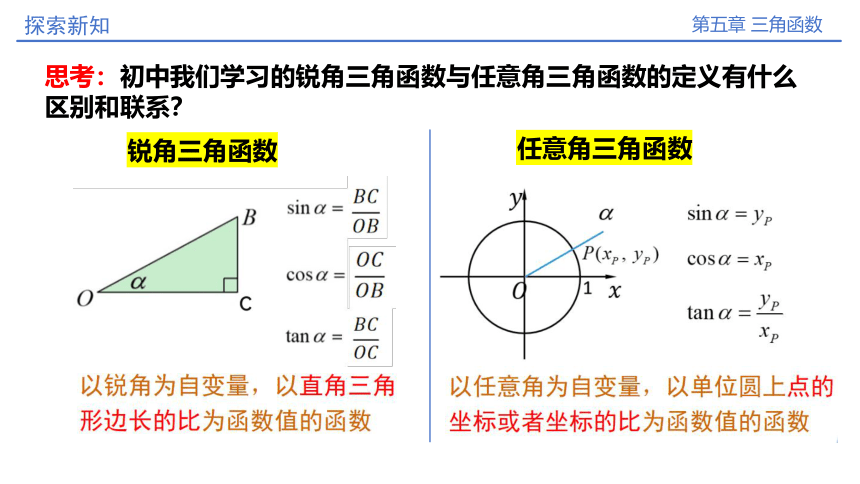
思考:初中我们学习的锐角三角函数与任意角三角函数的定义有什么区别和联系?
锐角三角函数
任意角三角函数
探索新知
P
解:如图,在直角坐标系中,作 ,
易知∠AOB的终边与单位圆的交点
坐标为 ,
所以
完成课本P180练习2.求的正弦、余弦和正切值.
典型例题
例2 如图,设α是一个任意角,它的终边上任意一点P(不与原点O重合)的坐标为(x,y),点P与原点的距离为r.求证:
α
结论:任意角α的三角函数值仅与α有关,与点P在角的终边上的位置无关.
∽
证明:设角的终边与单位圆交于点( ).分别过P, 作x轴的垂线PM,垂足分别为M,,则
典型例题
③ 叫做 的正切,即
任意角的三角函数第二定义
x
y
M
P (x,y)
课本P180练习3.已知角的终边过点P(-12,5),求角的三角函数值。
变式:已知角α的终边过点P(-12a,5a)(a≠0),求角α的三角函数值。
那么① 叫做 的正弦,即
② 叫做 的余弦,即
探索新知
设角 是一个任意角, 是终边上的任意一点,点 与原点的距离
α 0° 30° 45° 60° 90° 120° 135° 150° 180° 270° 360°
α的弧度
sin α
cos α
tan α
特殊角的三角函数值
-
-
-
-
-
探索新知
-
前面我们学习了三角函数的定义,根据已有的学习经验,你认为接下来应研究三角函数的哪些问题?
由三角函数的定义以及任意角α是的终边与单位圆交点所在的象限,你能发现三角函数值的符号有什么规律吗?
探索新知
三角函数 y=sinx y=cosx y=tanx
定义域
象限角三角函数值 符号
探究:根据任意角的三角函数的定义,确定正弦、余弦、正切函数在弧度制下的定义域,再确定这三种三角函数的值在各个象限的符号.
象限角函数值取正:一全二正弦,三切四余弦.
辨析1:判断正误.
(1)已知是三角形的内角,则必有( )
(2)若,则是第一或第二象限角.( )
(3)对于任意角,都有意义.( )
答案:√,×,×.
辨析2:若则在( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
答案:C.
典型例题
证明:先证充分性.
因为①式 sinθ<0成立,
所以θ角的终边可能位于第三或第四象限,
也可能与y轴的负半轴重合;
又因为②式tan θ>0成立,
所以θ角的终边可能位于第一或第三象限.
例3.求证:角θ为第三象限角的充要条件是
因为①②式都成立,
所以θ角的终边只能位于第三象限.
于是角θ为第三象限角.
典型例题
再证必要性.
因为①式sin θ<0成立,
由定义①②式都成立.
例3求证:角θ为第三象限角的充要条件是
典型例题
练习:
(1)若 ,试指出 所在的象限;
(2)若 在第三象限,判断 的符号.
第三象限
典型例题
探究2:现在我们尝试从三角函数的定义出发,讨论一下什么时候三角函数取值相等?
由三角函数的定义,可以知道:终边相同的角的同一三角函数的值相等.
由此,我们可以得到一组公式:
公式一
其中
探索新知
(1)诱导公式一体现了三角函数周期性取值的规律,这是“单位圆上的点绕圆周旋转整数周仍然回到原来位置”的特征的反映.
(2)利用公式一可以把求任意角的三角函数值,转化为求0~2π角的三角函数值.同时,由公式一可以发现,只要讨论清楚三角函数在区间[0,2π]上的性质,那么三角函数在整个定义域上的性质就清楚了.
(2)你认为诱导公式一有什么作用?
追问:(1)观察诱导公式一,对三角函数的取值规律你有什么进一步的发现?它反映了圆的什么特性?
探索新知
【例3】计算下列各式的值.
(1)sin(-1 395°)cos 1 110°+cos(-1 020°) sin 750°;
(4)sin 810°+cos 360°-tan 1 125°.
典型例题
课堂小结:
(1)任意角的三角函数的定义;
(2)三角函数值的符号;
(3)诱导公式一.
作业:
(1)整理本节课的题型;
(2)课本P182的练习15题.
课堂小结:
5.2 三角函数的概念
第五章 三角函数
5.2.1 三角函数的概念
探索新知
停顿
问题1 如何研究具体的函数类型,我们研究对数函数的路径是什么
背景
概念
图象和性质
应用
回顾:在初中我们是如何定义锐角三角函数的?
A
C
B
在Rt△ABC中,
它们是以锐角为自变量,边的比值为函数值的三角函数.
对边
邻边
斜边
特殊角的三角函数值
探索新知
上述定义只限于直角三角形中的锐角,而现在角的定义已经拓广到任意角,如:
停顿
师生互动,探索新知
问题2 如图:圆O上的点P以A为起点做逆时针方向旋转。如何借助角α的大小变化刻画点P的位置变化呢?
先研究单位圆上点P的变化情况。
﹒
探索新知
一般地,任意给定一个角 ∈R,它的终边OP与单位圆交点P的坐标,无论是横坐标x还是纵坐标y,都是唯一确定的.
所以,点P的横坐标x、纵坐标y都是角 的函数.
以原点O为圆心,以单位长度(r=1)为半径的圆称为单位圆。
y
o
x
1
M
探索新知
探索新知
任意角三角函数的定义
注意:正弦,余弦,正切都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数,我们将他们称为三角函数.
设 是一个任意角, ∈R ,它的终边OP与单位圆相交于点P(x,y).
(1)把点P的纵坐标y叫做 的正弦函数,记作sin , 即y=sin ;
(2)把点P的横坐标x叫做 的余弦函数,记作cos ,即x= cos ;
(3)把点P的纵坐标与横坐标的比值叫做 的正切,记作tan ,即=tan (x≠0).
﹒
我们将正弦函数、余弦函数和正切函数统称为三角函数,通常将它们记为:
正弦函数
余弦函数
正切函数
点P的纵坐标和横坐标的比值为函数值α的函数,称为正切函数.
思考:其中也是关于α的函数吗?为什么? α也可以取全体实数吗?
探索新知
根据三角函数的定义,确定它们的定义域(弧度制)
思
考
三角函数 定义域
R
R
﹒
探索新知
思考:初中我们学习的锐角三角函数与任意角三角函数的定义有什么区别和联系?
锐角三角函数
任意角三角函数
探索新知
P
解:如图,在直角坐标系中,作 ,
易知∠AOB的终边与单位圆的交点
坐标为 ,
所以
完成课本P180练习2.求的正弦、余弦和正切值.
典型例题
例2 如图,设α是一个任意角,它的终边上任意一点P(不与原点O重合)的坐标为(x,y),点P与原点的距离为r.求证:
α
结论:任意角α的三角函数值仅与α有关,与点P在角的终边上的位置无关.
∽
证明:设角的终边与单位圆交于点( ).分别过P, 作x轴的垂线PM,垂足分别为M,,则
典型例题
③ 叫做 的正切,即
任意角的三角函数第二定义
x
y
M
P (x,y)
课本P180练习3.已知角的终边过点P(-12,5),求角的三角函数值。
变式:已知角α的终边过点P(-12a,5a)(a≠0),求角α的三角函数值。
那么① 叫做 的正弦,即
② 叫做 的余弦,即
探索新知
设角 是一个任意角, 是终边上的任意一点,点 与原点的距离
α 0° 30° 45° 60° 90° 120° 135° 150° 180° 270° 360°
α的弧度
sin α
cos α
tan α
特殊角的三角函数值
-
-
-
-
-
探索新知
-
前面我们学习了三角函数的定义,根据已有的学习经验,你认为接下来应研究三角函数的哪些问题?
由三角函数的定义以及任意角α是的终边与单位圆交点所在的象限,你能发现三角函数值的符号有什么规律吗?
探索新知
三角函数 y=sinx y=cosx y=tanx
定义域
象限角三角函数值 符号
探究:根据任意角的三角函数的定义,确定正弦、余弦、正切函数在弧度制下的定义域,再确定这三种三角函数的值在各个象限的符号.
象限角函数值取正:一全二正弦,三切四余弦.
辨析1:判断正误.
(1)已知是三角形的内角,则必有( )
(2)若,则是第一或第二象限角.( )
(3)对于任意角,都有意义.( )
答案:√,×,×.
辨析2:若则在( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
答案:C.
典型例题
证明:先证充分性.
因为①式 sinθ<0成立,
所以θ角的终边可能位于第三或第四象限,
也可能与y轴的负半轴重合;
又因为②式tan θ>0成立,
所以θ角的终边可能位于第一或第三象限.
例3.求证:角θ为第三象限角的充要条件是
因为①②式都成立,
所以θ角的终边只能位于第三象限.
于是角θ为第三象限角.
典型例题
再证必要性.
因为①式sin θ<0成立,
由定义①②式都成立.
例3求证:角θ为第三象限角的充要条件是
典型例题
练习:
(1)若 ,试指出 所在的象限;
(2)若 在第三象限,判断 的符号.
第三象限
典型例题
探究2:现在我们尝试从三角函数的定义出发,讨论一下什么时候三角函数取值相等?
由三角函数的定义,可以知道:终边相同的角的同一三角函数的值相等.
由此,我们可以得到一组公式:
公式一
其中
探索新知
(1)诱导公式一体现了三角函数周期性取值的规律,这是“单位圆上的点绕圆周旋转整数周仍然回到原来位置”的特征的反映.
(2)利用公式一可以把求任意角的三角函数值,转化为求0~2π角的三角函数值.同时,由公式一可以发现,只要讨论清楚三角函数在区间[0,2π]上的性质,那么三角函数在整个定义域上的性质就清楚了.
(2)你认为诱导公式一有什么作用?
追问:(1)观察诱导公式一,对三角函数的取值规律你有什么进一步的发现?它反映了圆的什么特性?
探索新知
【例3】计算下列各式的值.
(1)sin(-1 395°)cos 1 110°+cos(-1 020°) sin 750°;
(4)sin 810°+cos 360°-tan 1 125°.
典型例题
课堂小结:
(1)任意角的三角函数的定义;
(2)三角函数值的符号;
(3)诱导公式一.
作业:
(1)整理本节课的题型;
(2)课本P182的练习15题.
课堂小结:
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
