河北省秦皇岛市青龙满族自治县部分学校2023-2024学年高一上学期12月月考数学试题(含解析)
文档属性
| 名称 | 河北省秦皇岛市青龙满族自治县部分学校2023-2024学年高一上学期12月月考数学试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 739.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 18:42:57 | ||
图片预览




文档简介
青龙满族自治县部分学校2023-2024学年高一上学期12月月考
数学试卷
本试卷共22题.全卷满分150分。考试用时120分钟。
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合,则( )
A. B. C. D.
2.若集合,,则
A. B. C. D.
3.命题“对任意的,”的否定是( ).
A.对任意的, B.对任意的,
C.存在, D.存在,
4.已知集合,,,则该函数的值域为( )
A. B. C. D.
5.函数的定义域是( ).
A.或 B. C. D.
6.已知为实数,且,则下列关系正确的是( )
A. B. C. D.
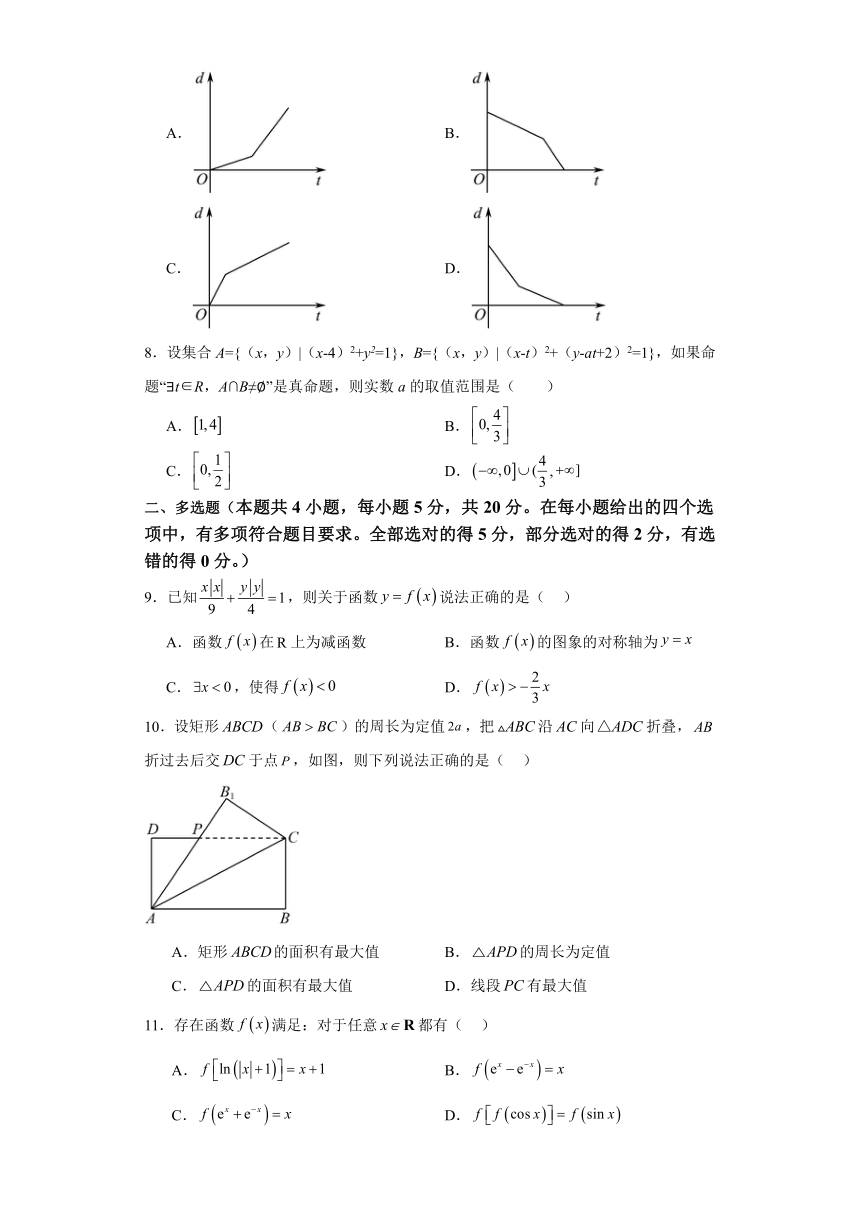
7.某学生从家出发去学校,为了保证不迟到,他先跑了一段路,然后一直走到学校.下列图中,纵轴表示该生离学校的距离d,横轴表示出发后的时间t,较符合该生走法的图像是( )
A. B.
C. D.
8.设集合A={(x,y)|(x-4)2+y2=1},B={(x,y)|(x-t)2+(y-at+2)2=1},如果命题“ t∈R,A∩B≠ ”是真命题,则实数a的取值范围是( )
A. B.
C. D.,
二、多选题(本题共4小题,每小题5分,共20分。在每小题给出的四个选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。)
9.已知,则关于函数说法正确的是( )
A.函数在上为减函数 B.函数的图象的对称轴为
C.,使得 D.
10.设矩形()的周长为定值,把沿向折叠,折过去后交于点,如图,则下列说法正确的是( )
A.矩形的面积有最大值 B.的周长为定值
C.的面积有最大值 D.线段有最大值
11.存在函数满足:对于任意都有( )
A. B.
C. D.
12.下列命题是真命题的是( )
A.若函数的定义域为,则函数的定义域为
B.函数(其中且)的图象过定点
C.函数的单调递减区间为
D.已知在上是增函数,则实数的取值范围是
第II卷(非选择题)
三、填空题:本题共4小题,每小题5分,共20分。
13.已知,则“”是“”的 条件.
14.已知函数是定义在上的奇函数,若时,,则 .
15.函数在区间上单调递减,则实数的取值范围为 .
16.已知幂函数的图象关于原点对称且与轴、轴均无交点,则整数的值为 .
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。17.设全集,,且.
(1)若,求.
(2)若,求实数a的取值范围.
18.已知幂函数在上单调递减.
(1)求的值;
(2)若函数的图象与轴交于,两点,求在上的值域.
19.设函数.
(1)若时,的值域为,求的值;
(2)若,求不等式的解集.
20.已知函数是定义在上的奇函数,且.
(1)求函数的解析式;
(2)判断并证明在上的单调性;
(3)若存在实数,使得不等式有解,求实数m的取值范围.
21.新型冠状病毒感染的肺炎治疗过程中,需要某医药公司生产的某种药品.此药品的年固定成本为250万元,每生产千件需另投入成本为.当年产量不足80千件时,(万元).当年产量不小于80千件时,(万元).每件商品售价为0.05万元,在疫情期间,该公司生产的药品能全部售完.
(Ⅰ)写出年利润(万元)关于年产量(千件)的函数解析式;
(Ⅱ)该公司决定将此药品所获利润的用来捐赠防疫物资.当年产量为多少千件时,在这一药品的生产中所获利润最大?此时可捐赠多少万元的物资款?
22.已知函数.
(1)求,的值;
(2)求证:是定值;
(3)求的值.
参考答案:
1.B
【详解】因为,所以,所以,
所以,
故选:B
2.C
【详解】由集合A得:(x-5)(x+1)=0,解得:x=5或x=-1,∴集合A={-1,5},
由集合B解得:x=1或x=-1,∴集合B={-1,1},
则A∩B={-1}.
故选C.3.D
【详解】原命题是全称量词命题,其否定是存在量词命题,
注意到要否定结论,所以D选项正确.
故选:D
4.A
【详解】由题意记,则,值域为.
故选:A.
5.A
【详解】分析:由真数大于0,利用分式不等式的解法即可得到答案.
详解:要使函数有意义,则,即,解得或,
∴函数的定义域是或.
故选.
点睛:本题考查函数的定义域及其求法.
6.C
【详解】由可知,,所以,则,即,A错误;
所以,B错误;
因,所以,所以,C正确;
当时,,D错误.
故选:C.
7.D
【详解】随着时间的增加,距学校的距离在减小,即函数图象应为减函数,排除A、C;
曲线的斜率反映行进的速度,斜率的绝对值越大速度越大,步行后速度变小,故排除B,所以较符合该生走法的图像是选项D所给的图形.
故选:D
8.B
【详解】∵A={(x,y)|(x-4)2+y2=1},表示平面坐标系中以M(4,0)为圆心,半径为1的圆,
B={(x,y)|(x-t)2+(y-at+2)2=1},表示以N(t,at-2)为圆心,半径为1的圆,且其圆心N在直线ax-y-2=0上,如图.
如果命题“ t∈R,A∩B≠ ”是真命题,即两圆有公共点,则圆心M到直线ax-y-2=0的距离不大于2,
即≤2,解得0≤a≤.
∴实数a的取值范围是[0,];
故选B.
9.AD
【分析】利用不同象限表示不同的圆锥曲线图象可求解.
【详解】当时,原等式化为,
当时,原等式化为,
当时,原等式化为,
当时,原等式化为,此方程无解,
结合椭圆、双曲线的图象作出图象如下:
由图象可知,函数在上为减函数,所以A正确;
第一象限的图象为椭圆的部分,不关于,所以B错误;
函数图象不出现在第三象限,所以不存在,使得,
所以C错误;
因为第四象限部分双曲线的渐近线与第二象限的双曲线部分的渐近线都为,所以结合函数图象恒成立,所以D正确.
故选:AD.
10.BC
【详解】设,则,因为,所以.
矩形的面积,
因为,所以无最大值.故A错.
根据图形折叠可知与全等,
所以周长为.故B正确.
设,则,有,即,得,,当时,取最大值.故C正确.,
因为函数在上单调递减,在上单调递增,
所以当,当时函数有最小值,无最大值.故D错误.
故选:BC.
11.BD
【分析】AC可举出反例,BD可写出符合要求的函数.
【详解】A选项,时得,2,函数值不唯一,A错误;
C选项,时得函数值不唯一,C错误;
B选项,满足要求;
D选项,满足要求.
故选:BD
12.BD
【详解】对于A,的定义域为,即,,
的定义域为,A错误;
对于B,,图象过定点,B正确;
对于C,令,由知:,
在上单调递增,在上单调递减,
又在上单调递增,的单调递减区间为,C错误;
对于D,在上是增函数,,解得:,
即实数的取值范围为,D正确.
故选:BD.
13.充分非必要
【详解】若,即,
解得:或,
集合 或,
所以“”是“”的充分非必要条件.
故答案为:充分非必要
14.
【详解】根据函数的奇偶性的性质可得
.
故答案为.
【点睛】本题主要考查函数值的计算,结合函数奇偶性的性质进行转化是解决本题的关键.
15.
【详解】因为函数在区间上单调递减,
所以,
即,
则实数的取值范围为;
故答案为:.
16.
【详解】因为函数为幂函数,所以解得或,
当时,幂函数为,不满足题意,舍去;
当时,幂函数为,满足关于原点对称且与轴、轴均无交点,
故答案为:.
17.(1),;(2).
(2)根据集合的包含关系求参数的取值范围.
【详解】(1)因为,所以,所以或
又因为且,
所以;
(2)因为且,
所以当时,则;当,则;
综上实数a的取值范围为.
18.(1)
(2)
【详解】(1)由题意得,
解得或,且,即,
所以
故.
(2)由(1)得,
由题意得,6是方程的两个根,
则
解得,,
因为为开口向上的二次函数,且对称轴为,
因此在上单调递减,在上单调递增,
所以,,
故在上的值域为.
19.(1)1;(2)见解析
【详解】(1)由题意,,且,即.
又,故
1°当时,,不合题意,舍;
2°当时,,得;
3°当时,,得.
综上得,;
(2)由,得,从而得,
故等价于,即,
∴,令.
注意到,若,则的两根同号.且两根为:;
由得或.
①当时,,∵,∴,
这时,
所以解集为或;
②当时,,∵,∴,
这时,,
所以解集为或;
③当时,,∵,∴,
这时,
所以解集为且;
④当时,,∵,∴,这时,所以解集为且;
⑤当时,,∵,∴,这时恒成立,所以解集为;
20.(1)
(2)在上单调递增,证明见解析
(3)
【详解】(1)∵为定义在上的奇函数,∴,则有
由得,∴,
又,∴,,;
(2)任取,,
∵,∴,,且,,
∴,∴,在上单调递增;
(3)由(2)知在上单调递增,∴,
.
令,则有
令,,,∴.
21.(Ⅰ);(Ⅱ)当年产量为100千件时,该厂在这一药品生产中所获利润最大,可捐赠10万元物资款.
【解析】(Ⅰ)根据题意得千件药品销售额为万元,进而得;
(Ⅱ)当时,由二次函数性质得当时,取得最大值万元,当时,由基本不等式得当时,取得最大值1000万元,进而得年产量为100千件时,该厂在这一药品生产中所获利润最大,可捐赠10万元物资款.
【详解】(Ⅰ)因为每件药品售价为0.05万元,则千件药品销售额为万元,
依题意得:
当时,.
当时,.
所以.
(Ⅱ)当时,.
此时,当时,取得最大值万元.
当时,.
此时,即时,取得最大值1000万元.
由于,所以当年产量为100千件时,该厂在这一药品生产中所获利润最大,
此时可捐赠10万元物资款.
22.(1)2,2;(2)见证明;(3).
【分析】(1)利用函数的解析式,通过,分别求解,的值;(2)利用函数的解析式化简,即可证明是定值;(3)利用(2)的结论分组,即可求解的值.
【详解】(1)函数.
时,,.
(2)因为,
所以.
(3)
.
数学试卷
本试卷共22题.全卷满分150分。考试用时120分钟。
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合,则( )
A. B. C. D.
2.若集合,,则
A. B. C. D.
3.命题“对任意的,”的否定是( ).
A.对任意的, B.对任意的,
C.存在, D.存在,
4.已知集合,,,则该函数的值域为( )
A. B. C. D.
5.函数的定义域是( ).
A.或 B. C. D.
6.已知为实数,且,则下列关系正确的是( )
A. B. C. D.
7.某学生从家出发去学校,为了保证不迟到,他先跑了一段路,然后一直走到学校.下列图中,纵轴表示该生离学校的距离d,横轴表示出发后的时间t,较符合该生走法的图像是( )
A. B.
C. D.
8.设集合A={(x,y)|(x-4)2+y2=1},B={(x,y)|(x-t)2+(y-at+2)2=1},如果命题“ t∈R,A∩B≠ ”是真命题,则实数a的取值范围是( )
A. B.
C. D.,
二、多选题(本题共4小题,每小题5分,共20分。在每小题给出的四个选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。)
9.已知,则关于函数说法正确的是( )
A.函数在上为减函数 B.函数的图象的对称轴为
C.,使得 D.
10.设矩形()的周长为定值,把沿向折叠,折过去后交于点,如图,则下列说法正确的是( )
A.矩形的面积有最大值 B.的周长为定值
C.的面积有最大值 D.线段有最大值
11.存在函数满足:对于任意都有( )
A. B.
C. D.
12.下列命题是真命题的是( )
A.若函数的定义域为,则函数的定义域为
B.函数(其中且)的图象过定点
C.函数的单调递减区间为
D.已知在上是增函数,则实数的取值范围是
第II卷(非选择题)
三、填空题:本题共4小题,每小题5分,共20分。
13.已知,则“”是“”的 条件.
14.已知函数是定义在上的奇函数,若时,,则 .
15.函数在区间上单调递减,则实数的取值范围为 .
16.已知幂函数的图象关于原点对称且与轴、轴均无交点,则整数的值为 .
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。17.设全集,,且.
(1)若,求.
(2)若,求实数a的取值范围.
18.已知幂函数在上单调递减.
(1)求的值;
(2)若函数的图象与轴交于,两点,求在上的值域.
19.设函数.
(1)若时,的值域为,求的值;
(2)若,求不等式的解集.
20.已知函数是定义在上的奇函数,且.
(1)求函数的解析式;
(2)判断并证明在上的单调性;
(3)若存在实数,使得不等式有解,求实数m的取值范围.
21.新型冠状病毒感染的肺炎治疗过程中,需要某医药公司生产的某种药品.此药品的年固定成本为250万元,每生产千件需另投入成本为.当年产量不足80千件时,(万元).当年产量不小于80千件时,(万元).每件商品售价为0.05万元,在疫情期间,该公司生产的药品能全部售完.
(Ⅰ)写出年利润(万元)关于年产量(千件)的函数解析式;
(Ⅱ)该公司决定将此药品所获利润的用来捐赠防疫物资.当年产量为多少千件时,在这一药品的生产中所获利润最大?此时可捐赠多少万元的物资款?
22.已知函数.
(1)求,的值;
(2)求证:是定值;
(3)求的值.
参考答案:
1.B
【详解】因为,所以,所以,
所以,
故选:B
2.C
【详解】由集合A得:(x-5)(x+1)=0,解得:x=5或x=-1,∴集合A={-1,5},
由集合B解得:x=1或x=-1,∴集合B={-1,1},
则A∩B={-1}.
故选C.3.D
【详解】原命题是全称量词命题,其否定是存在量词命题,
注意到要否定结论,所以D选项正确.
故选:D
4.A
【详解】由题意记,则,值域为.
故选:A.
5.A
【详解】分析:由真数大于0,利用分式不等式的解法即可得到答案.
详解:要使函数有意义,则,即,解得或,
∴函数的定义域是或.
故选.
点睛:本题考查函数的定义域及其求法.
6.C
【详解】由可知,,所以,则,即,A错误;
所以,B错误;
因,所以,所以,C正确;
当时,,D错误.
故选:C.
7.D
【详解】随着时间的增加,距学校的距离在减小,即函数图象应为减函数,排除A、C;
曲线的斜率反映行进的速度,斜率的绝对值越大速度越大,步行后速度变小,故排除B,所以较符合该生走法的图像是选项D所给的图形.
故选:D
8.B
【详解】∵A={(x,y)|(x-4)2+y2=1},表示平面坐标系中以M(4,0)为圆心,半径为1的圆,
B={(x,y)|(x-t)2+(y-at+2)2=1},表示以N(t,at-2)为圆心,半径为1的圆,且其圆心N在直线ax-y-2=0上,如图.
如果命题“ t∈R,A∩B≠ ”是真命题,即两圆有公共点,则圆心M到直线ax-y-2=0的距离不大于2,
即≤2,解得0≤a≤.
∴实数a的取值范围是[0,];
故选B.
9.AD
【分析】利用不同象限表示不同的圆锥曲线图象可求解.
【详解】当时,原等式化为,
当时,原等式化为,
当时,原等式化为,
当时,原等式化为,此方程无解,
结合椭圆、双曲线的图象作出图象如下:
由图象可知,函数在上为减函数,所以A正确;
第一象限的图象为椭圆的部分,不关于,所以B错误;
函数图象不出现在第三象限,所以不存在,使得,
所以C错误;
因为第四象限部分双曲线的渐近线与第二象限的双曲线部分的渐近线都为,所以结合函数图象恒成立,所以D正确.
故选:AD.
10.BC
【详解】设,则,因为,所以.
矩形的面积,
因为,所以无最大值.故A错.
根据图形折叠可知与全等,
所以周长为.故B正确.
设,则,有,即,得,,当时,取最大值.故C正确.,
因为函数在上单调递减,在上单调递增,
所以当,当时函数有最小值,无最大值.故D错误.
故选:BC.
11.BD
【分析】AC可举出反例,BD可写出符合要求的函数.
【详解】A选项,时得,2,函数值不唯一,A错误;
C选项,时得函数值不唯一,C错误;
B选项,满足要求;
D选项,满足要求.
故选:BD
12.BD
【详解】对于A,的定义域为,即,,
的定义域为,A错误;
对于B,,图象过定点,B正确;
对于C,令,由知:,
在上单调递增,在上单调递减,
又在上单调递增,的单调递减区间为,C错误;
对于D,在上是增函数,,解得:,
即实数的取值范围为,D正确.
故选:BD.
13.充分非必要
【详解】若,即,
解得:或,
集合 或,
所以“”是“”的充分非必要条件.
故答案为:充分非必要
14.
【详解】根据函数的奇偶性的性质可得
.
故答案为.
【点睛】本题主要考查函数值的计算,结合函数奇偶性的性质进行转化是解决本题的关键.
15.
【详解】因为函数在区间上单调递减,
所以,
即,
则实数的取值范围为;
故答案为:.
16.
【详解】因为函数为幂函数,所以解得或,
当时,幂函数为,不满足题意,舍去;
当时,幂函数为,满足关于原点对称且与轴、轴均无交点,
故答案为:.
17.(1),;(2).
(2)根据集合的包含关系求参数的取值范围.
【详解】(1)因为,所以,所以或
又因为且,
所以;
(2)因为且,
所以当时,则;当,则;
综上实数a的取值范围为.
18.(1)
(2)
【详解】(1)由题意得,
解得或,且,即,
所以
故.
(2)由(1)得,
由题意得,6是方程的两个根,
则
解得,,
因为为开口向上的二次函数,且对称轴为,
因此在上单调递减,在上单调递增,
所以,,
故在上的值域为.
19.(1)1;(2)见解析
【详解】(1)由题意,,且,即.
又,故
1°当时,,不合题意,舍;
2°当时,,得;
3°当时,,得.
综上得,;
(2)由,得,从而得,
故等价于,即,
∴,令.
注意到,若,则的两根同号.且两根为:;
由得或.
①当时,,∵,∴,
这时,
所以解集为或;
②当时,,∵,∴,
这时,,
所以解集为或;
③当时,,∵,∴,
这时,
所以解集为且;
④当时,,∵,∴,这时,所以解集为且;
⑤当时,,∵,∴,这时恒成立,所以解集为;
20.(1)
(2)在上单调递增,证明见解析
(3)
【详解】(1)∵为定义在上的奇函数,∴,则有
由得,∴,
又,∴,,;
(2)任取,,
∵,∴,,且,,
∴,∴,在上单调递增;
(3)由(2)知在上单调递增,∴,
.
令,则有
令,,,∴.
21.(Ⅰ);(Ⅱ)当年产量为100千件时,该厂在这一药品生产中所获利润最大,可捐赠10万元物资款.
【解析】(Ⅰ)根据题意得千件药品销售额为万元,进而得;
(Ⅱ)当时,由二次函数性质得当时,取得最大值万元,当时,由基本不等式得当时,取得最大值1000万元,进而得年产量为100千件时,该厂在这一药品生产中所获利润最大,可捐赠10万元物资款.
【详解】(Ⅰ)因为每件药品售价为0.05万元,则千件药品销售额为万元,
依题意得:
当时,.
当时,.
所以.
(Ⅱ)当时,.
此时,当时,取得最大值万元.
当时,.
此时,即时,取得最大值1000万元.
由于,所以当年产量为100千件时,该厂在这一药品生产中所获利润最大,
此时可捐赠10万元物资款.
22.(1)2,2;(2)见证明;(3).
【分析】(1)利用函数的解析式,通过,分别求解,的值;(2)利用函数的解析式化简,即可证明是定值;(3)利用(2)的结论分组,即可求解的值.
【详解】(1)函数.
时,,.
(2)因为,
所以.
(3)
.
同课章节目录
