苏教版六年级年级下册数学总复习 数与代数 数的四则混合运算(课件)(共38张PPT)
文档属性
| 名称 | 苏教版六年级年级下册数学总复习 数与代数 数的四则混合运算(课件)(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 18:09:24 | ||
图片预览











文档简介
(共38张PPT)
总复习
1.数与代数
数的四则混合运算
七
你能说说四则混合运算的运算顺序吗?
(教材第76页)
算式里有括号
算式里没有括号
只有小括号
有小括号和中括号
只有加、减法或只有乘、除法(同级运算)
既有乘、除法,又有加、减法(两级运算)
先算小括号里面的,再算小括号外面的
先算小括号里面的,再算中括号里面的,最后算中括号外面的
从左往右按顺序计算
先算乘、除法,再算加、减法
四则混合运算
名称 举例
用字母表示
加法交换律 18+25=25+18
加法结合律
乘法交换律
乘法结合律
乘法分配律
65+75+25
=65+(75+25)
23×4=4×23
78×125×8
=78×(125×8)
8×(125+2)
=8×125+8×2
整理已经学过的运算律,并填写下表。
运算性质
一个加数不变,另一个加数增加或减少一个数,和也增加或减少同一个数。
一个加数增加一个数,另一个加数减少同一个数,和不变。
和的变化规律
减数不变,被减数增加或减少一个数,差也增加或减少同一个数。
被减数不变,减数增加或减少一个数,差减少或增加同一个数。
差的变化规律
被减数和减数都增加或减少同一个数,差不变。
一个因数不变,另一个因数乘几或除以几(0除外),积也乘几或除以几。
一个因数乘几,另一个因数除以相同的数(0除外),积不变。
积的变化规律
除数不变,被除数乘几或除以几(0除外),商也乘几或除以几。
被除数不变,除数乘几或除以几(0除外),商除以几或乘几。
商的变化规律
被除数和除数都乘或除以一个相同的数(0除外),商不变。
(教材第76页)
1. 260 - 49 - 156 ( 5.9 + 1.65) ÷ 0.25
18 ÷ 1.5 - 0.15 (1.5- 0.6)×(3-1.8)
= 211 - 156
= 55
= 7.55 ÷ 0.25
= 30.2
= 12 - 0.15
= 11.85
= 0.9 × 1.2
= 1.08
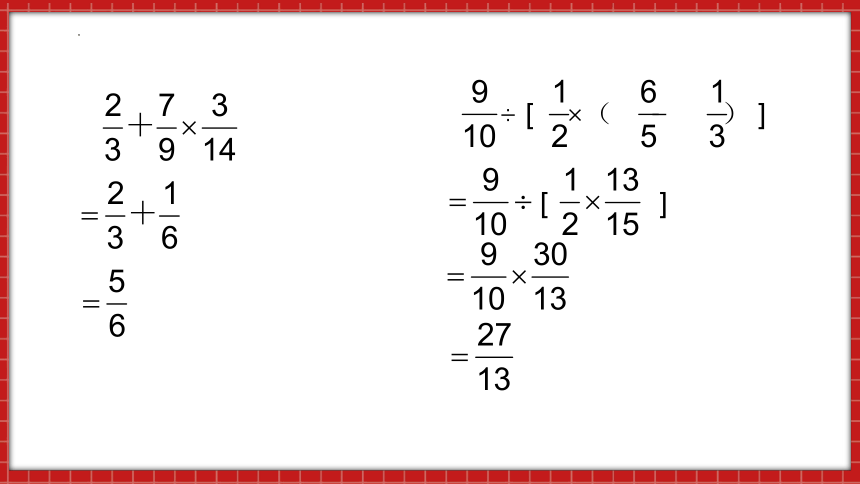
÷ [ ×( - ) ]
[ ]
2. 下面各题, 怎样算简便就怎样算。
4×0.27×25 3.8×99+3.8 560÷16÷5
= 4×25×0.27
= 100×0.27
= 27
= 3.8×(99+1)
= 3.8 × 100
= 380
= 560÷(16 × 5)
= 560÷ 90
= 7
2. 下面各题, 怎样算简便就怎样算。
(8+ )÷4
( ) ( )
( )
今天要栽50棵杨树和46棵柳树。
共有6个小组。
平均每个小组要栽多少棵?
3.
(50+46)÷6
= 96÷6
= 16(棵)
答:平均每个小组要栽16棵。
20-4.5×3
= 20 - 13.5
= 6.5(吨)
答:仓库里还有6.5吨大豆。
4.仓库里原来有20 吨大豆,运走了3 车,每车4.5 吨。仓库里还有多少吨大豆?
25×24×14
= 600×14
= 8400(个)
答:这篇文章一共有8400个字。
5.一篇文章原稿有14页,每页24行,每行25个字。这篇文章一共有多少个字?如果改排成每行28个字,每页30 行,这篇文章要排多少页?
8400÷28÷30
= 300÷30
= 10(页)
答:这篇文章要排10页。
6.先观察前两题的计算过程,再照样子计算后三题。
9×9-1=9×(10-1)-1=9×10-9-1=80
98×9-2=98×(10-1)-2=980-98-2=880
987×9-3=
9876×9-4=
98765×9-5=
987×(10-1)-3=9870-987-3=8880
9876×(10-1)-4=98760-9876-4=88880
98765×(10-1)-5=987650-98765-5=
888880
7.小华家七、八、九月三个月的用电量如下表:
(1)八月份的用电量比七月份增加了百分之几?
方法一
84-70 =14(千瓦·时)
14÷70= 0.2=20%
方法二
84÷70 =120%
120%-100% =20%
答:八月份的用电量比七月份增加了20%。
7.小华家七、八、九月三个月的用电量如下表:
(2)九月份的用电量比七月份节约了百分之几?比八月份呢?
方法一 70-60 =10(千瓦·时) 10÷70 ≈ 0.14=14%
答:九月份的用电量比七月份节约了14%,比八月份大约节约了29%。
84-60 =24(千瓦·时) 24÷84 ≈ 0.29=29%
7.小华家七、八、九月三个月的用电量如下表:
(2)九月份的用电量比七月份节约了百分之几?比八月份呢?
方法二 60÷70 ≈ 0.86=86% 100%-86% =14%
答:九月份的用电量比七月份节约了14%,比八月份大约节约了29%。
60÷84 ≈ 0.71=71% 100%-71% =29%
8.某商场有奖销售活动设置了10000 张奖券,其中一、 二、 三等奖的中奖率分别是5%、10%和30%。
(1) 一等奖和二等奖的奖券一共有多少张?
10000×5%=500(张)10000×10%=1000(张)
500+1000=1500(张)
答:一等奖和二等奖的奖券一共有1500张。
(2)你还能提出什么问题?
9.(1)三信小学美术组有63人,舞蹈组有56人。美术组的人数比舞蹈组多几分之几?
(63-56) ÷ 56
=7÷56
=0.125
=12.5%
答:美术组的人数比舞蹈组多12.5%。
答:舞蹈组有56人。
(2)三信小学美术组有63 人,舞蹈组的人数比美术组少 。舞蹈组有多少人?
63-63×
= 63 - 7
= 56(人)
9.(1)三信小学美术组有63人,舞蹈组有56人。美术组的人数比舞蹈组多几分之几?
(2)三信小学美术组有63 人,舞蹈组的人数比美术组少 。舞蹈组有多少人?
9.(1)三信小学美术组有63人,舞蹈组有56人。美术组的人数比舞蹈组多几分之几?
(3)三信小学美术组有63人, 比舞蹈组的人数多。舞蹈组有多少人?
9.(3)三信小学美术组有63人, 比舞蹈组的人数多。舞蹈组有多少人?
解:设舞蹈组有x 人。
x + x = 63
x = 63
x = 56
答:舞蹈组有56人。
10.(1)一袋大米,先用去 ,又用去,两次一共用去 6千克。这袋大米原来有多少千克?
解:设这袋大米原来有x 千克。
(+ )x = 6
x = 10
x = 6
答:这袋大米原来有10千克。
10.(2)一袋大米,先用去,又用去千克,两次一共用去千克。这袋大米原来有多少千克?
解:设这袋大米原来有x千克。
x+ =
x = 10
x = 2
答:这袋大米原来有10千克。
1.计算,能简算的要简算。
(1) ÷ 8× ÷
1
4
8
9
8
9
9
8
1
8
1
4
= × × ×
8
9
9
8
8
9
1
8
1
4
=( × )×( × )
=
1
32
除以一个不为0的数,等于乘这个数的倒数。
乘法结合律
巩固练习
3
4
(2)12.7×7.5-26× -75%
=12.7×7.5-26×0.75-1×0.75
把分数(百分数)改写成小数,并把最后一个数看作这个数乘1。
一个因数乘10,另一个因数除以10,积不变。
=127×0.75-26×0.75-1×0.75
=(127-26-1)×0.75
有公有的因数0.75,逆用乘法分配律。
=100×0.75
=75
2
19
(3)( + )×19×23
运用乘法分配律
有括号先算括号里面的
=46+57
(4)(1.5+0.6)×(3-1.8)
=2.1×1.2
=2.52
3
23
3
23
2
19
= ×19×23+ ×19×23
=2×23+3×19
=103
(5) + + +…+
逆用乘法分配律
1
1×4
1
4×7
1
7×10
1
97×100
= ×(1- )+ ×( - )
+ ×( - )+…+ ×( - )
1
3
1
4
1
3
1
4
1
7
1
3
1
7
1
10
1
3
1
97
1
100
= ×(1- + - + - +…+ - )
1
3
1
4
1
4
1
7
1
7
1
10
1
97
1
100
= ×(1- )
1
3
1
100
=
33
100
……
= -
1
7
1
4
3
4×7
= -
1
4
1
1
3
1×4
2.填一填。
现价÷原价=折扣
(1)一本书现价6.4元,比原价便宜1.6元。这本书是打( )折出售的。
八
6.4÷(6.4+1.6)=80%=八折
(2)用50粒种子做发芽试验,有7粒种子未发芽。这些种子的发芽率是( )。
发芽率=发芽粒数÷总粒数
(50-7)÷50=86%
86%
(3)某玩具厂上午卖出玩具1.5万个,下午卖出同样的玩具2.3万个。下午卖出的比上午卖出的多收入10.8万元,平均每个玩具卖( )元。
总数量÷总份数=平均数;
多收入的总价对应多卖出的数量。
10.8÷(2.3-1.5)
=10.8÷0.8
=13.5(元)
13.5
(4)张阿姨开着车以80千米/时的速度在一条路上行驶,前方出现限速60千米/时的标志。如果张阿姨继续保持原来的速度,那么她将受到扣( )分的处罚。
超速50%及以上,扣12分;超速20%及以上未达到50%,扣6分;超速未达到20%,扣3分。
(80-60)÷60 ≈ 33.3%
20%<33.3%<50%
要求超速百分之几就用“超过限速的部分÷限速”
6
(5)有一条3米长的彩带,先剪去全长的-,又剪去-米,这时还剩下( )米。
1
3
1
3
53
-
第一次剪去的是全长的-,
第二次剪去的是-米,不一样长。
13
13
3-3×---=-(米)
13
13
53
两次剪去的一样长吗?
3.学生夏令营组织远足,原计划3小时走完11.25 km。实际2.5小时就走完了全程。实际比原计划每小时多走多少千米?
速度=路程÷时间,分别求出实际和原计划的速度就可以求出实际比原计划每小时多走多少千米。
11.25÷2.5-11.25÷3
=4.5-3.75
=0.75(km)
答:实际比原计划每小时多走0.75 km。
4.六年级办公室买进一包白纸,计划每天用25张,可以用20天。由于注意了节约用纸,实际每天只用了20张,实际比计划多用多少天?
实际比计划多用多少天
实际用的天数
计划用的天数
-
总张数
实际每天用的张数
÷
计划每天用的张数
计划用的天数
×
25×20÷20-20
=500÷20-20
=25-20
=5(天)
答:实际比计划多用了5天。
4.六年级办公室买进一包白纸,计划每天用25张,可以用20天。由于注意了节约用纸,实际每天只用了20张,实际比计划多用多少天?
分析法:从应用题的问题出发,去寻找解答这个问题所必须的条件。
5.一个旅游景点去年全年接待游客约196万人,上半年接待游客数是全年的-。第三季度接待游客数是上半年的-,第三季度接待游客多少人?
3
7
3
4
上半年游客数=全年游客数×-
3
7
第三季度游客数=上半年游客数×-
3
4
196×-×-
3
7
3
4
=63(万人)
=630000(人)
答:第三季度接待游客630000人。
解决分数应用题的关键是找准单位“1”。
1.一种食用油,原来每升售价为12元,现在由于成本提高,单价提高了25%。原来买10 L的钱,现在能买多少升?
12×(1+25%)=15(元)
12×10÷15=8(L)
答:现在能买8 L。
现在单价=原来单价×(1+25%)
数量=总价÷单价
拓展提升
2.假设规定“*”为一种新的运算,符合a * b=(a×b)÷(a+b),如:3 * 7=(3×7)÷(3+7)=2.1,请依照例子计算:(4 * 2)* 3。
(4 * 2)* 3
=[(4×2)÷(4+2)]* 3
=- * 3
=(-×3)÷(-+3)
=—
先代入小括号里面的
4
3
4
3
4
3
12
13
要正确理解新定义的算式含义,严格按照新定义的计算顺序,将数值代入算式中,再把它转化为一般的四则运算进行计算。
总复习
1.数与代数
数的四则混合运算
七
你能说说四则混合运算的运算顺序吗?
(教材第76页)
算式里有括号
算式里没有括号
只有小括号
有小括号和中括号
只有加、减法或只有乘、除法(同级运算)
既有乘、除法,又有加、减法(两级运算)
先算小括号里面的,再算小括号外面的
先算小括号里面的,再算中括号里面的,最后算中括号外面的
从左往右按顺序计算
先算乘、除法,再算加、减法
四则混合运算
名称 举例
用字母表示
加法交换律 18+25=25+18
加法结合律
乘法交换律
乘法结合律
乘法分配律
65+75+25
=65+(75+25)
23×4=4×23
78×125×8
=78×(125×8)
8×(125+2)
=8×125+8×2
整理已经学过的运算律,并填写下表。
运算性质
一个加数不变,另一个加数增加或减少一个数,和也增加或减少同一个数。
一个加数增加一个数,另一个加数减少同一个数,和不变。
和的变化规律
减数不变,被减数增加或减少一个数,差也增加或减少同一个数。
被减数不变,减数增加或减少一个数,差减少或增加同一个数。
差的变化规律
被减数和减数都增加或减少同一个数,差不变。
一个因数不变,另一个因数乘几或除以几(0除外),积也乘几或除以几。
一个因数乘几,另一个因数除以相同的数(0除外),积不变。
积的变化规律
除数不变,被除数乘几或除以几(0除外),商也乘几或除以几。
被除数不变,除数乘几或除以几(0除外),商除以几或乘几。
商的变化规律
被除数和除数都乘或除以一个相同的数(0除外),商不变。
(教材第76页)
1. 260 - 49 - 156 ( 5.9 + 1.65) ÷ 0.25
18 ÷ 1.5 - 0.15 (1.5- 0.6)×(3-1.8)
= 211 - 156
= 55
= 7.55 ÷ 0.25
= 30.2
= 12 - 0.15
= 11.85
= 0.9 × 1.2
= 1.08
÷ [ ×( - ) ]
[ ]
2. 下面各题, 怎样算简便就怎样算。
4×0.27×25 3.8×99+3.8 560÷16÷5
= 4×25×0.27
= 100×0.27
= 27
= 3.8×(99+1)
= 3.8 × 100
= 380
= 560÷(16 × 5)
= 560÷ 90
= 7
2. 下面各题, 怎样算简便就怎样算。
(8+ )÷4
( ) ( )
( )
今天要栽50棵杨树和46棵柳树。
共有6个小组。
平均每个小组要栽多少棵?
3.
(50+46)÷6
= 96÷6
= 16(棵)
答:平均每个小组要栽16棵。
20-4.5×3
= 20 - 13.5
= 6.5(吨)
答:仓库里还有6.5吨大豆。
4.仓库里原来有20 吨大豆,运走了3 车,每车4.5 吨。仓库里还有多少吨大豆?
25×24×14
= 600×14
= 8400(个)
答:这篇文章一共有8400个字。
5.一篇文章原稿有14页,每页24行,每行25个字。这篇文章一共有多少个字?如果改排成每行28个字,每页30 行,这篇文章要排多少页?
8400÷28÷30
= 300÷30
= 10(页)
答:这篇文章要排10页。
6.先观察前两题的计算过程,再照样子计算后三题。
9×9-1=9×(10-1)-1=9×10-9-1=80
98×9-2=98×(10-1)-2=980-98-2=880
987×9-3=
9876×9-4=
98765×9-5=
987×(10-1)-3=9870-987-3=8880
9876×(10-1)-4=98760-9876-4=88880
98765×(10-1)-5=987650-98765-5=
888880
7.小华家七、八、九月三个月的用电量如下表:
(1)八月份的用电量比七月份增加了百分之几?
方法一
84-70 =14(千瓦·时)
14÷70= 0.2=20%
方法二
84÷70 =120%
120%-100% =20%
答:八月份的用电量比七月份增加了20%。
7.小华家七、八、九月三个月的用电量如下表:
(2)九月份的用电量比七月份节约了百分之几?比八月份呢?
方法一 70-60 =10(千瓦·时) 10÷70 ≈ 0.14=14%
答:九月份的用电量比七月份节约了14%,比八月份大约节约了29%。
84-60 =24(千瓦·时) 24÷84 ≈ 0.29=29%
7.小华家七、八、九月三个月的用电量如下表:
(2)九月份的用电量比七月份节约了百分之几?比八月份呢?
方法二 60÷70 ≈ 0.86=86% 100%-86% =14%
答:九月份的用电量比七月份节约了14%,比八月份大约节约了29%。
60÷84 ≈ 0.71=71% 100%-71% =29%
8.某商场有奖销售活动设置了10000 张奖券,其中一、 二、 三等奖的中奖率分别是5%、10%和30%。
(1) 一等奖和二等奖的奖券一共有多少张?
10000×5%=500(张)10000×10%=1000(张)
500+1000=1500(张)
答:一等奖和二等奖的奖券一共有1500张。
(2)你还能提出什么问题?
9.(1)三信小学美术组有63人,舞蹈组有56人。美术组的人数比舞蹈组多几分之几?
(63-56) ÷ 56
=7÷56
=0.125
=12.5%
答:美术组的人数比舞蹈组多12.5%。
答:舞蹈组有56人。
(2)三信小学美术组有63 人,舞蹈组的人数比美术组少 。舞蹈组有多少人?
63-63×
= 63 - 7
= 56(人)
9.(1)三信小学美术组有63人,舞蹈组有56人。美术组的人数比舞蹈组多几分之几?
(2)三信小学美术组有63 人,舞蹈组的人数比美术组少 。舞蹈组有多少人?
9.(1)三信小学美术组有63人,舞蹈组有56人。美术组的人数比舞蹈组多几分之几?
(3)三信小学美术组有63人, 比舞蹈组的人数多。舞蹈组有多少人?
9.(3)三信小学美术组有63人, 比舞蹈组的人数多。舞蹈组有多少人?
解:设舞蹈组有x 人。
x + x = 63
x = 63
x = 56
答:舞蹈组有56人。
10.(1)一袋大米,先用去 ,又用去,两次一共用去 6千克。这袋大米原来有多少千克?
解:设这袋大米原来有x 千克。
(+ )x = 6
x = 10
x = 6
答:这袋大米原来有10千克。
10.(2)一袋大米,先用去,又用去千克,两次一共用去千克。这袋大米原来有多少千克?
解:设这袋大米原来有x千克。
x+ =
x = 10
x = 2
答:这袋大米原来有10千克。
1.计算,能简算的要简算。
(1) ÷ 8× ÷
1
4
8
9
8
9
9
8
1
8
1
4
= × × ×
8
9
9
8
8
9
1
8
1
4
=( × )×( × )
=
1
32
除以一个不为0的数,等于乘这个数的倒数。
乘法结合律
巩固练习
3
4
(2)12.7×7.5-26× -75%
=12.7×7.5-26×0.75-1×0.75
把分数(百分数)改写成小数,并把最后一个数看作这个数乘1。
一个因数乘10,另一个因数除以10,积不变。
=127×0.75-26×0.75-1×0.75
=(127-26-1)×0.75
有公有的因数0.75,逆用乘法分配律。
=100×0.75
=75
2
19
(3)( + )×19×23
运用乘法分配律
有括号先算括号里面的
=46+57
(4)(1.5+0.6)×(3-1.8)
=2.1×1.2
=2.52
3
23
3
23
2
19
= ×19×23+ ×19×23
=2×23+3×19
=103
(5) + + +…+
逆用乘法分配律
1
1×4
1
4×7
1
7×10
1
97×100
= ×(1- )+ ×( - )
+ ×( - )+…+ ×( - )
1
3
1
4
1
3
1
4
1
7
1
3
1
7
1
10
1
3
1
97
1
100
= ×(1- + - + - +…+ - )
1
3
1
4
1
4
1
7
1
7
1
10
1
97
1
100
= ×(1- )
1
3
1
100
=
33
100
……
= -
1
7
1
4
3
4×7
= -
1
4
1
1
3
1×4
2.填一填。
现价÷原价=折扣
(1)一本书现价6.4元,比原价便宜1.6元。这本书是打( )折出售的。
八
6.4÷(6.4+1.6)=80%=八折
(2)用50粒种子做发芽试验,有7粒种子未发芽。这些种子的发芽率是( )。
发芽率=发芽粒数÷总粒数
(50-7)÷50=86%
86%
(3)某玩具厂上午卖出玩具1.5万个,下午卖出同样的玩具2.3万个。下午卖出的比上午卖出的多收入10.8万元,平均每个玩具卖( )元。
总数量÷总份数=平均数;
多收入的总价对应多卖出的数量。
10.8÷(2.3-1.5)
=10.8÷0.8
=13.5(元)
13.5
(4)张阿姨开着车以80千米/时的速度在一条路上行驶,前方出现限速60千米/时的标志。如果张阿姨继续保持原来的速度,那么她将受到扣( )分的处罚。
超速50%及以上,扣12分;超速20%及以上未达到50%,扣6分;超速未达到20%,扣3分。
(80-60)÷60 ≈ 33.3%
20%<33.3%<50%
要求超速百分之几就用“超过限速的部分÷限速”
6
(5)有一条3米长的彩带,先剪去全长的-,又剪去-米,这时还剩下( )米。
1
3
1
3
53
-
第一次剪去的是全长的-,
第二次剪去的是-米,不一样长。
13
13
3-3×---=-(米)
13
13
53
两次剪去的一样长吗?
3.学生夏令营组织远足,原计划3小时走完11.25 km。实际2.5小时就走完了全程。实际比原计划每小时多走多少千米?
速度=路程÷时间,分别求出实际和原计划的速度就可以求出实际比原计划每小时多走多少千米。
11.25÷2.5-11.25÷3
=4.5-3.75
=0.75(km)
答:实际比原计划每小时多走0.75 km。
4.六年级办公室买进一包白纸,计划每天用25张,可以用20天。由于注意了节约用纸,实际每天只用了20张,实际比计划多用多少天?
实际比计划多用多少天
实际用的天数
计划用的天数
-
总张数
实际每天用的张数
÷
计划每天用的张数
计划用的天数
×
25×20÷20-20
=500÷20-20
=25-20
=5(天)
答:实际比计划多用了5天。
4.六年级办公室买进一包白纸,计划每天用25张,可以用20天。由于注意了节约用纸,实际每天只用了20张,实际比计划多用多少天?
分析法:从应用题的问题出发,去寻找解答这个问题所必须的条件。
5.一个旅游景点去年全年接待游客约196万人,上半年接待游客数是全年的-。第三季度接待游客数是上半年的-,第三季度接待游客多少人?
3
7
3
4
上半年游客数=全年游客数×-
3
7
第三季度游客数=上半年游客数×-
3
4
196×-×-
3
7
3
4
=63(万人)
=630000(人)
答:第三季度接待游客630000人。
解决分数应用题的关键是找准单位“1”。
1.一种食用油,原来每升售价为12元,现在由于成本提高,单价提高了25%。原来买10 L的钱,现在能买多少升?
12×(1+25%)=15(元)
12×10÷15=8(L)
答:现在能买8 L。
现在单价=原来单价×(1+25%)
数量=总价÷单价
拓展提升
2.假设规定“*”为一种新的运算,符合a * b=(a×b)÷(a+b),如:3 * 7=(3×7)÷(3+7)=2.1,请依照例子计算:(4 * 2)* 3。
(4 * 2)* 3
=[(4×2)÷(4+2)]* 3
=- * 3
=(-×3)÷(-+3)
=—
先代入小括号里面的
4
3
4
3
4
3
12
13
要正确理解新定义的算式含义,严格按照新定义的计算顺序,将数值代入算式中,再把它转化为一般的四则运算进行计算。
