3.1 用表格表示的变量间关系 同步课件(共28张PPT)
文档属性
| 名称 | 3.1 用表格表示的变量间关系 同步课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:36:40 | ||
图片预览








文档简介
(共28张PPT)
3.1 用表格表示
的变量间关系
学习目标
1)在具体情境中理解什么是变量、自变量、因变量,并能举出反映变量之间关系的例子。
2)学会用表格整理试验得出的数据,能从表格中获得变量之间关系的信息,并根据表格中的资料尝试对变化趋势进行初步的预测。
重点:理解变量、自变量、因变量的概念。
难点:从表格中获取变量间关系的信息,能分析变量之间的变化趋势,进行初步预测。
春天
夏天
秋天
冬天
观察下列图片,你发现了什么?
春
夏
秋
万物都在悄悄地发生着变化,从数学的角度研究它们之间的关系,将有助于我们更好地认识世界,预测未来,那就让我们一起来揭开变化的新篇章吧…
观察小车从不同的高度上滑落相同的距离,你发现了什么?
3次小车从不同的高度上滑落的时间为3s,1s,0.5s
支撑物越高,下滑时间越短。
根据上表回答下列问题:
问题一 支撑物高度为70厘米时,小车下滑时间是多少?
问题二 如果用h表示支撑物高度,t表示小车下滑时间,随着h逐渐
变大,t的变化趋势是什么?
支撑物高度/cm 10 20 30 40 50 60 70 80 90 100
小车下滑时间/s 4.23 3.00 2.45 2.13 1.89 1.71 1.59 1.50 1.41 1.35
1.59秒
由表格信息可知,随着h的增加,t逐渐减小。
根据上表回答下列问题:
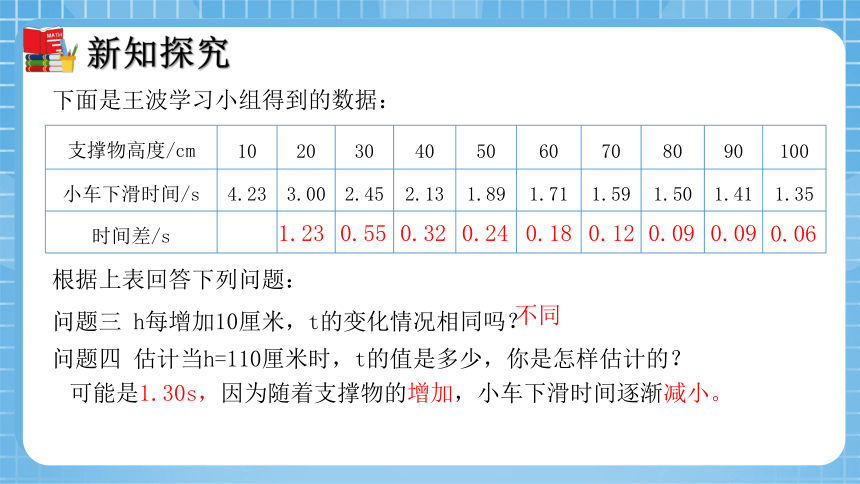
问题三 h每增加10厘米,t的变化情况相同吗?
问题四 估计当h=110厘米时,t的值是多少,你是怎样估计的?
下面是王波学习小组得到的数据:
支撑物高度/cm 10 20 30 40 50 60 70 80 90 100
小车下滑时间/s 4.23 3.00 2.45 2.13 1.89 1.71 1.59 1.50 1.41 1.35
时间差/s
1.23
0.55
0.32
0.24
0.18
0.12
0.09
0.09
0.06
不同
可能是1.30s,因为随着支撑物的增加,小车下滑时间逐渐减小。
根据上表回答下列问题:
问题五 随着支撑物高度h的变化,还有哪些量发生变化?哪些量
始终不发生变化?
下面是王波学习小组得到的数据:
支撑物高度/cm 10 20 30 40 50 60 70 80 90 100
小车下滑时间/s 4.23 3.00 2.45 2.13 1.89 1.71 1.59 1.50 1.41 1.35
时间差/s
1.23
0.55
0.32
0.24
0.18
0.12
0.09
0.09
0.06
小车下滑时间发生了变化,木板的长度没变化。
在“小车下滑的时间”中,支撑物的高度h和小车下滑的时间t都在变化,它们都是变量(variable).其中小车下滑的时间t随支撑物的高度h的变化而变化.支撑物的高度h是自变量(independent variale),小车下滑的时间t是因变量(dependent variale).
在这一变化过程中,小车下滑的距离(木板的长度)一直没有变化.像这种在变化过程中数值始终不变的量叫作常量(constant).
我国从1949年到2009年的人口统计数据如下(精确到0.01亿):
时间/年 1949 1959 1969 1979 1989 1999 2009
人口/亿 5.42 6.72 8.07 9.75 11.07 12.59 13.35
解:随着x的增加,y也增加.
(1)如果用x表示时间,y表示我国人口总数,那么随着x的变化,y的变化趋势是什么?
我国从1949年到2009年的人口统计数据如下(精确到0.01亿):
时间/年 1949 1959 1969 1979 1989 1999 2009
人口/亿 5.42 6.72 8.07 9.75 11.07 12.59 13.35
(2)从1949年起,时间每向后推移10年,我国人口是怎样的变化?
解:从1949年起,时间每向后推移10年,我国人口增加1.5亿左右,但最后10年的增加量大约只有0.76亿.
把自变量x的一系列取值和因变量的对应值列成一个表格来表示变量之间的关系,像这种表示变量之间关系的方法叫做表格法.
在表中,我国人口总数y随时间x的变化而变化,x是自变量,y是因变量.
分析表格常分三步:
第一步,是通过表格确定自变量与因变量
第二步,是纵向观察每一列,发现因变量与自变量的对应关系
第三步,是分别横向观察两栏,从中发现两变量间星现的变化趋势。求因变量的值,若不在所列数值之中,则家根据两变量之间的变化趋势进行估计。
定义:一般地,在某一变化过程中,数值发生变化的量叫做变量.在变化过程中,数值始终不变的量叫做常量.
变量
自变量
因变量
主动变化的量
被动变化的量
变量包括自变量、因变量。
自变量是自然发生变化的量;
因变量是随其他量的变化而变化的量
常量是数值始终不变的量
例1.父亲告诉小明:“距离地面越远,温度越低”,并且出示了下面的表格:
父亲给小明出了下面几个问题,请你和小明一起回答:
距离地面高度(千米) 0 1 2 3 4 5
温度(°C) 20 14 8 2 -4 -10
根据规律,高度每升高1千米,温度降低6℃,
所以距离地面6千米时的温度是-10-6=-16(℃).
(1)如果用h表示距离地面的高度,用t表示温度,那么随着h的变化,t如何变化?
随着h的升高,t在降低.
(2)你知道距离地面5千米的高空温度是多少吗?
-10℃.
(3)你能预测出距离地面6千米的高空温度是多少吗?
1. 一个圆柱的高h为10 cm,当圆柱的底面半径r由小到大变化时,圆柱的体积V也发生了变化,在这个变化过程中( )
A. r是因变量,V是自变量
B. r是自变量,V是因变量
C. r是自变量,h是因变量
D. h是自变量,V是因变量
B
2.对于圆的周长公式C=2πR,下列说法正确的是( )
A.π,R是变量,2是常量
B.R是变量,π是常量
C.C是变量,π,R是常量
D.C,R是变量,2,π是常量
3.刘师傅到加油站加油,如图是所用的加油机上的某一时刻数据显示牌,则其中的变量是( )
A.金额 B.金额和数量
C.数量 D.单价
4.骆驼被称为“沙漠之舟”,它的体温是随时间的变化而变化的,在这一问题中,因变量是( )
A.沙漠 B.体温
C.时间 D.骆驼
x 0 1 2 3 4 …
y 8 8.5 9 9.5 10 …
5.(弹簧挂重物后会伸长,测得弹簧长度y(cm)最长为20cm,与所挂物体重量x(kg)间有下面的关系:下列说法不正确的是( )
A.x与y都是变量,x是自变量,y是因变量
B.所挂物体为6kg,弹簧长度为11cm
C.体每增加1kg,弹簧长度就增加0.5cm
D.挂30kg物体时一定比原长增加15cm
【详解】解:A.因为弹簧长度随所挂物体的重量的变化而变化,所以是自变量,是因变量.故本选项正确,不符合题意;
B.当所挂物体为时,弹簧的长度为.故本选项正确,不符合题意;
C.从表格数据中分析可知,物体每增加,弹簧长度就增加.故本选项正确,不符合题意;
D.当所挂物体为时,弹簧长度为.故本选项不正确,符合题意.故选:D
6.下表所列为某商店薄利多销的情况.某商品原价为560元,随着不同幅度的降价,日销量(单位:件)发生相应的变化(如表):
这个表反映了____个变量之间的关系,_____是自变量,_______是因变量.从表中可以看出每降价5元,日销量增加____件,从而可以估计降价之前的日销量为____件.
降价(元) 5 10 15 20 25 30
日销量(件) 780 810 840 870 900 930
7.下表是某公共电话亭打长途电话的几次收费记录:
(1)上表反映了哪两个变量间的关系?哪个是自变量?哪个是因变量?
(2)如果用x表示时间,y表示电话费,那么随x的变化,y的变化趋势是什么?
(3)丽丽打了5分钟电话,那么电话费需付多少元?
(1)上表反应的是时间和电话费两个变量之间的关系,时间是自变量,电话费是因变量;
(2)根据图表数据得出:随着x的增大,y相应的也增大;
(3)由图表中数据直接得出:丽丽打了5分钟电话,那么电话费需付3元.
8.某公交车每月的支出费用为4000元,每月的乘车人数 (人)与每月利润(利润=收入费用-支出费用) (元)的变化关系如下表所示(每位乘客的公交票价是固定不变的);
(1)在这个变化过程中, 是自变量, 是因变量;(填中文)
(2)观察表中数据可知,每月乘客量达到 人以上时,该公交车才不会亏损;
【详解】解:(1)在这个变化过程中,每月的乘车人数是自变量,每月利润是因变量;
(2) ∵观察表中数据可知,当每月乘客量达到2000人以上时,每月利润为0,
∴每月乘客量达到2000人以上时,该公交车才不会亏损;
8.某公交车每月的支出费用为4000元,每月的乘车人数 (人)与每月利润(利润=收入费用-支出费用) (元)的变化关系如下表所示(每位乘客的公交票价是固定不变的);
(3)请你估计当每月乘车人数为3500人时,每月利润为 元?
(4)若5月份想获得利润5000元,则请你估计5月份的乘客量需达 人.
(3) ∵每月乘客量增加500人时,每月利润增加1000元,
∴当每月乘车人数为3500人时,每月利润为3000元;
(4) ∵每月乘客量增加500人时,每月利润增加1000元,
∴若5月份想获得利润5000元,5月份的乘客量需达4500人.
1.自变量是在一定范围内主动变化的量.
2.因变量是随自变量变化而变化的量.
自变量
因变量
被动变化的量
变量
主动变化的量
3.表格可以表示因变量随自变量变化而变化的情况,还能帮助我们对变化趋势进行初步的预测.
习题3.1
第1、2题
3.1 用表格表示
的变量间关系
学习目标
1)在具体情境中理解什么是变量、自变量、因变量,并能举出反映变量之间关系的例子。
2)学会用表格整理试验得出的数据,能从表格中获得变量之间关系的信息,并根据表格中的资料尝试对变化趋势进行初步的预测。
重点:理解变量、自变量、因变量的概念。
难点:从表格中获取变量间关系的信息,能分析变量之间的变化趋势,进行初步预测。
春天
夏天
秋天
冬天
观察下列图片,你发现了什么?
春
夏
秋
万物都在悄悄地发生着变化,从数学的角度研究它们之间的关系,将有助于我们更好地认识世界,预测未来,那就让我们一起来揭开变化的新篇章吧…
观察小车从不同的高度上滑落相同的距离,你发现了什么?
3次小车从不同的高度上滑落的时间为3s,1s,0.5s
支撑物越高,下滑时间越短。
根据上表回答下列问题:
问题一 支撑物高度为70厘米时,小车下滑时间是多少?
问题二 如果用h表示支撑物高度,t表示小车下滑时间,随着h逐渐
变大,t的变化趋势是什么?
支撑物高度/cm 10 20 30 40 50 60 70 80 90 100
小车下滑时间/s 4.23 3.00 2.45 2.13 1.89 1.71 1.59 1.50 1.41 1.35
1.59秒
由表格信息可知,随着h的增加,t逐渐减小。
根据上表回答下列问题:
问题三 h每增加10厘米,t的变化情况相同吗?
问题四 估计当h=110厘米时,t的值是多少,你是怎样估计的?
下面是王波学习小组得到的数据:
支撑物高度/cm 10 20 30 40 50 60 70 80 90 100
小车下滑时间/s 4.23 3.00 2.45 2.13 1.89 1.71 1.59 1.50 1.41 1.35
时间差/s
1.23
0.55
0.32
0.24
0.18
0.12
0.09
0.09
0.06
不同
可能是1.30s,因为随着支撑物的增加,小车下滑时间逐渐减小。
根据上表回答下列问题:
问题五 随着支撑物高度h的变化,还有哪些量发生变化?哪些量
始终不发生变化?
下面是王波学习小组得到的数据:
支撑物高度/cm 10 20 30 40 50 60 70 80 90 100
小车下滑时间/s 4.23 3.00 2.45 2.13 1.89 1.71 1.59 1.50 1.41 1.35
时间差/s
1.23
0.55
0.32
0.24
0.18
0.12
0.09
0.09
0.06
小车下滑时间发生了变化,木板的长度没变化。
在“小车下滑的时间”中,支撑物的高度h和小车下滑的时间t都在变化,它们都是变量(variable).其中小车下滑的时间t随支撑物的高度h的变化而变化.支撑物的高度h是自变量(independent variale),小车下滑的时间t是因变量(dependent variale).
在这一变化过程中,小车下滑的距离(木板的长度)一直没有变化.像这种在变化过程中数值始终不变的量叫作常量(constant).
我国从1949年到2009年的人口统计数据如下(精确到0.01亿):
时间/年 1949 1959 1969 1979 1989 1999 2009
人口/亿 5.42 6.72 8.07 9.75 11.07 12.59 13.35
解:随着x的增加,y也增加.
(1)如果用x表示时间,y表示我国人口总数,那么随着x的变化,y的变化趋势是什么?
我国从1949年到2009年的人口统计数据如下(精确到0.01亿):
时间/年 1949 1959 1969 1979 1989 1999 2009
人口/亿 5.42 6.72 8.07 9.75 11.07 12.59 13.35
(2)从1949年起,时间每向后推移10年,我国人口是怎样的变化?
解:从1949年起,时间每向后推移10年,我国人口增加1.5亿左右,但最后10年的增加量大约只有0.76亿.
把自变量x的一系列取值和因变量的对应值列成一个表格来表示变量之间的关系,像这种表示变量之间关系的方法叫做表格法.
在表中,我国人口总数y随时间x的变化而变化,x是自变量,y是因变量.
分析表格常分三步:
第一步,是通过表格确定自变量与因变量
第二步,是纵向观察每一列,发现因变量与自变量的对应关系
第三步,是分别横向观察两栏,从中发现两变量间星现的变化趋势。求因变量的值,若不在所列数值之中,则家根据两变量之间的变化趋势进行估计。
定义:一般地,在某一变化过程中,数值发生变化的量叫做变量.在变化过程中,数值始终不变的量叫做常量.
变量
自变量
因变量
主动变化的量
被动变化的量
变量包括自变量、因变量。
自变量是自然发生变化的量;
因变量是随其他量的变化而变化的量
常量是数值始终不变的量
例1.父亲告诉小明:“距离地面越远,温度越低”,并且出示了下面的表格:
父亲给小明出了下面几个问题,请你和小明一起回答:
距离地面高度(千米) 0 1 2 3 4 5
温度(°C) 20 14 8 2 -4 -10
根据规律,高度每升高1千米,温度降低6℃,
所以距离地面6千米时的温度是-10-6=-16(℃).
(1)如果用h表示距离地面的高度,用t表示温度,那么随着h的变化,t如何变化?
随着h的升高,t在降低.
(2)你知道距离地面5千米的高空温度是多少吗?
-10℃.
(3)你能预测出距离地面6千米的高空温度是多少吗?
1. 一个圆柱的高h为10 cm,当圆柱的底面半径r由小到大变化时,圆柱的体积V也发生了变化,在这个变化过程中( )
A. r是因变量,V是自变量
B. r是自变量,V是因变量
C. r是自变量,h是因变量
D. h是自变量,V是因变量
B
2.对于圆的周长公式C=2πR,下列说法正确的是( )
A.π,R是变量,2是常量
B.R是变量,π是常量
C.C是变量,π,R是常量
D.C,R是变量,2,π是常量
3.刘师傅到加油站加油,如图是所用的加油机上的某一时刻数据显示牌,则其中的变量是( )
A.金额 B.金额和数量
C.数量 D.单价
4.骆驼被称为“沙漠之舟”,它的体温是随时间的变化而变化的,在这一问题中,因变量是( )
A.沙漠 B.体温
C.时间 D.骆驼
x 0 1 2 3 4 …
y 8 8.5 9 9.5 10 …
5.(弹簧挂重物后会伸长,测得弹簧长度y(cm)最长为20cm,与所挂物体重量x(kg)间有下面的关系:下列说法不正确的是( )
A.x与y都是变量,x是自变量,y是因变量
B.所挂物体为6kg,弹簧长度为11cm
C.体每增加1kg,弹簧长度就增加0.5cm
D.挂30kg物体时一定比原长增加15cm
【详解】解:A.因为弹簧长度随所挂物体的重量的变化而变化,所以是自变量,是因变量.故本选项正确,不符合题意;
B.当所挂物体为时,弹簧的长度为.故本选项正确,不符合题意;
C.从表格数据中分析可知,物体每增加,弹簧长度就增加.故本选项正确,不符合题意;
D.当所挂物体为时,弹簧长度为.故本选项不正确,符合题意.故选:D
6.下表所列为某商店薄利多销的情况.某商品原价为560元,随着不同幅度的降价,日销量(单位:件)发生相应的变化(如表):
这个表反映了____个变量之间的关系,_____是自变量,_______是因变量.从表中可以看出每降价5元,日销量增加____件,从而可以估计降价之前的日销量为____件.
降价(元) 5 10 15 20 25 30
日销量(件) 780 810 840 870 900 930
7.下表是某公共电话亭打长途电话的几次收费记录:
(1)上表反映了哪两个变量间的关系?哪个是自变量?哪个是因变量?
(2)如果用x表示时间,y表示电话费,那么随x的变化,y的变化趋势是什么?
(3)丽丽打了5分钟电话,那么电话费需付多少元?
(1)上表反应的是时间和电话费两个变量之间的关系,时间是自变量,电话费是因变量;
(2)根据图表数据得出:随着x的增大,y相应的也增大;
(3)由图表中数据直接得出:丽丽打了5分钟电话,那么电话费需付3元.
8.某公交车每月的支出费用为4000元,每月的乘车人数 (人)与每月利润(利润=收入费用-支出费用) (元)的变化关系如下表所示(每位乘客的公交票价是固定不变的);
(1)在这个变化过程中, 是自变量, 是因变量;(填中文)
(2)观察表中数据可知,每月乘客量达到 人以上时,该公交车才不会亏损;
【详解】解:(1)在这个变化过程中,每月的乘车人数是自变量,每月利润是因变量;
(2) ∵观察表中数据可知,当每月乘客量达到2000人以上时,每月利润为0,
∴每月乘客量达到2000人以上时,该公交车才不会亏损;
8.某公交车每月的支出费用为4000元,每月的乘车人数 (人)与每月利润(利润=收入费用-支出费用) (元)的变化关系如下表所示(每位乘客的公交票价是固定不变的);
(3)请你估计当每月乘车人数为3500人时,每月利润为 元?
(4)若5月份想获得利润5000元,则请你估计5月份的乘客量需达 人.
(3) ∵每月乘客量增加500人时,每月利润增加1000元,
∴当每月乘车人数为3500人时,每月利润为3000元;
(4) ∵每月乘客量增加500人时,每月利润增加1000元,
∴若5月份想获得利润5000元,5月份的乘客量需达4500人.
1.自变量是在一定范围内主动变化的量.
2.因变量是随自变量变化而变化的量.
自变量
因变量
被动变化的量
变量
主动变化的量
3.表格可以表示因变量随自变量变化而变化的情况,还能帮助我们对变化趋势进行初步的预测.
习题3.1
第1、2题
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
