3.2 用关系式表示的变量间关系 同步课件(共31张PPT)
文档属性
| 名称 | 3.2 用关系式表示的变量间关系 同步课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 00:00:00 | ||
图片预览








文档简介
3.2 用关系式表示
的变量间关系
学习目标
1)理解两个变量之间的关系可以用关系式表示,能在一个关系式中指出自变量和因变量。
2)能够在具体的情境中列出表示变量关系的关系式。
重点:能够在具体的情境中列出表示变量关系的关系式。
难点:能用适当的函数表示方法刻画简单实际问题中变量之间的关系。
在“小车下滑的时间”中,
1.支撑物的高度h和小车下滑的时间t都在变化,它们都是变量.其中小车下滑的时间t随支撑物的高度h的变化而变化,
2.支撑物的高度h是自变量,
3.小车下滑的时间t是因变量.
常量、变量、自变量、因变量:
2.在某一变化过程中,不断变化的量叫作变量.
3.如果一个变量y随另一个变量x的变化而变化,则把x叫作自变量 ,y叫作因变量.
1.在变化过程中数值始终不变的量叫做常量.
游戏:数青蛙
一只青蛙一张嘴,两只眼睛四条腿;
两只青蛙两张嘴,四只眼睛八条腿;
三只青蛙三张嘴,六只眼睛十二条腿;
……
1.青蛙的眼睛数和只数有关系吗?能用数学式表达吗?
2.青蛙的腿数和只数有关系吗?能用数学式表达吗?
这个游戏你能继续玩下去吗?
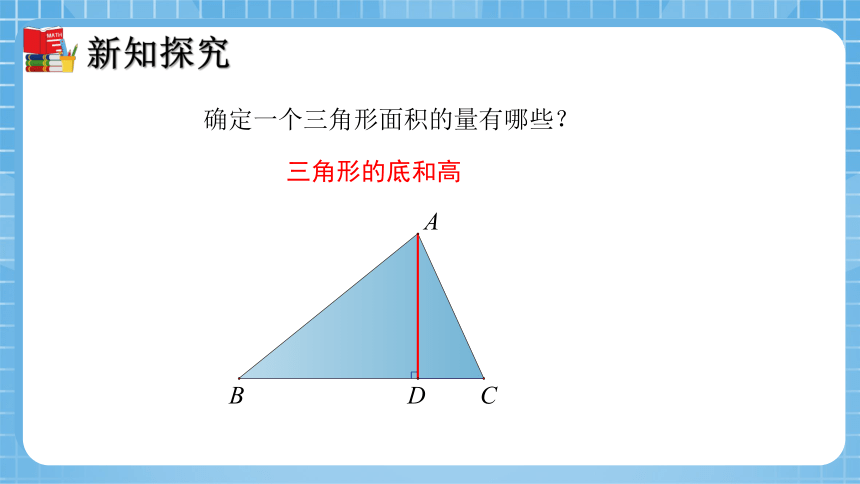
确定一个三角形面积的量有哪些?
D
B
C
A
三角形的底和高
用关系式表示变量间的关系
A
B
C
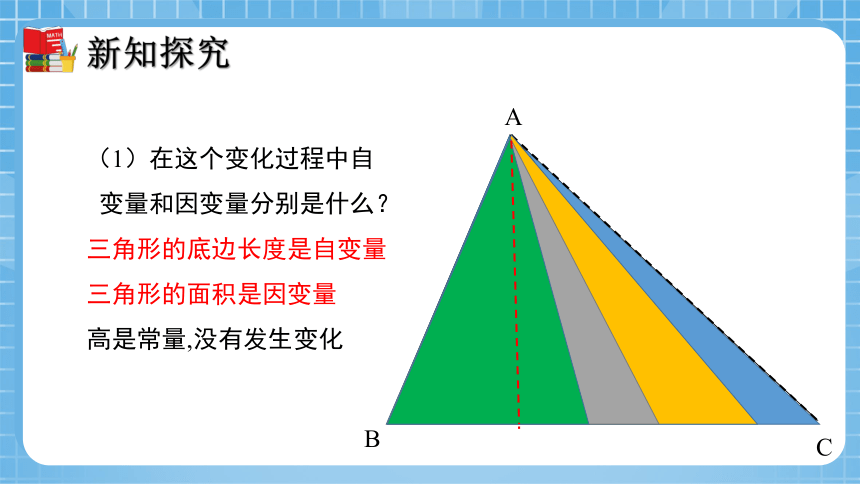
如图,△ABC底边BC上的高是6厘米。当三角形的顶点C沿底边所在的直线向B运动时,三角形的面积发生了怎样的变化?
(1)在这个变化过程中自
变量和因变量分别是什么?
三角形的底边长度是自变量
三角形的面积是因变量
高是常量,没有发生变化
A
B
C
A
B
C
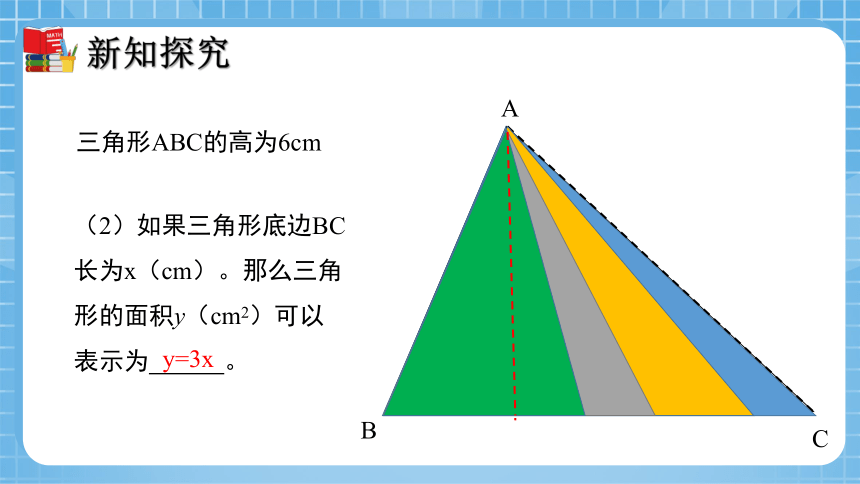
三角形ABC的高为6cm
(2)如果三角形底边BC长为x(cm)。那么三角形的面积y(cm2)可以表示为 。
y=3x
A
B
C
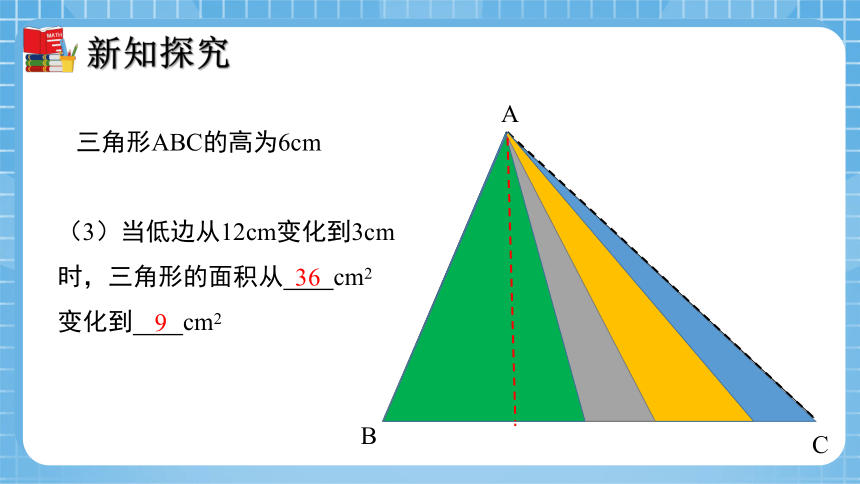
三角形ABC的高为6cm
(3)当低边从12cm变化到3cm时,三角形的面积从 cm2 变化到 cm2
36
9
y=3x表示了 和 之间的关系,它是变量y随x变化的关系式。
三角形底边长
三角形面积
关系式是我们表示变量之间关系的另一种方法.
你能直观地表示这个关系式吗?
y=3x 表示了_________________和______之间的关系,它是变量_____随_____变化的关系式。
三角形底边边长 x
面积y
y
x
3x
含自变量代数式
因变量
系数为1
=
y
因变量要单独写在等式的左边
自变量x
关系式y=3x
因变量y
关系式是我们表示变量之间关系的另一种方法.
你还记得圆锥的体积公式是什么吗?
其中的字母表示什么?
如图,圆锥的高度是4厘米,当圆锥的底面半径由小到大变化时,圆锥的体积也随之发生了变化.
问题一 在这个变化过程中,自变量、因变量各是什么?
问题二 如果圆锥底面半径为 r(cm),那么圆锥的体积V(cm3)与r的关系式为________.
问题三 当底面半径由1cm变化到10cm时,圆锥的体积由 cm3变化到 cm3 .
圆锥的底面半径的长度是自变量,圆锥的体积是因变量。
V=43πr2
?
43π
?
4003π
?
例1.汽车在行驶过程中,由于惯性的作用刹车后仍将滑行一段距离才能停住,这段距离称为刹车距离.刹车距离是分析事故原因的一个重要因素.
某型号的汽车在平整路面上的刹车距离sm与车速vkm/h之间有下列经验公式:
(1)式中哪个量是常量?哪个量是变量?哪个量是自变量?哪个量是因变量?
(2)当刹车时车速v 分别是40、80、120km/h时,相应的滑行距离s分别是多少?
256 s,v v s.
当v=40km/h时, s=6.25m;
当 v=80km/h时, s=25m;
当 v=120km/h时,s=56.25m.
你知道什么是“低碳生活”吗?“低碳生活”是指人们生活中尽量减少所耗能量,从而降低碳、特别是二氧化碳的排放量的一种方式.
你知道什么是“低碳生活”吗?“低碳生活”是指人们生活中尽量减少所耗能量,从而降低碳、特别是二氧化碳的排放量的一种方式。
问题一 用字母表示家居用电的二氧化碳排放量的公式为_____________,其中的字母表示________________
______________________.
问题二 在上述关系式中,耗电量每增加 1 kW·h,二氧化碳排放量增加_________。当耗电量从 1 kW·h 增加到100 kW·h 时,二氧化碳排放量从________增加到____________。
问题三 小明家本月用电大约110 kW·h、天然气20m3、自来水5 t、油耗75 L,请你计算一下小明家这几项的二氧化碳排放量。
y = 0.785x
耗电量(x)和二氧化碳排放量(y)
0.785 kg
0.785 kg
78.5 kg
家居用电的二氧化碳:110×0.785=86.35(kg)
开私家车的二氧化碳:75×2.7=202.5(kg)
家用天然气的二氧化碳:20×0.19=3.8(kg)
家用自来水的二氧化碳:5×0.91=4.55(kg)
例2.某工厂现在年产值是15万元,计划今后每年增加2万元.
(1)年产值y(万元)与年数x之间的关系式为 __________;
(2)5年后的年产值是______万元.
解析:(1)根据题意可知,现在年产值是15万元,计划今后
每年增加2万元,x年后增加2x万元,所以年产值y(万元)与年数x之间的关系式为y=2x+15;
(2)将x=5代入关系式得:y=2x+15=2×5+15=25.
y=2x+15
25
1. 汽车在匀速行驶过程中,路程s、速度v和时间t之间的关系为s=vt,下列说法正确的是( )
A. s,v,t都是变量
B. s,t是变量,v是常量
C. v,t是变量,s是常量
D. s,v是变量,t是常量
B
2.变量x与y之间的关系式是y=x2-3,当自变量x=2时,因变量y的值是( )
A.-2 B.-1 C.1 D.2
3. 如果每盒笔售价16元,共有10支,用y(元)表示笔的售价,x(支)表示笔的数量,那么y与x的关系式为( )
A. y=10x B. y=16x
C. y=?8?5x D. y=?5?8x
?
C
4.百货大楼进了一批花布,出售时要在进价(进货价格)的基础上加一定的利润,其长度x与售价y如下表:
{5940675A-B579-460E-94D1-54222C63F5DA}长度x/m
1
2
3
4
…
售价y/元
8+0.3
16+0.6
24+0.9
32+1.2
…
下列用长度x表示售价y的关系式中,正确的是( )
A.y=8x+0.3 B.y=(8+0.3)x
C.y=8+0.3x D.y=8+0.3+x
{5940675A-B579-460E-94D1-54222C63F5DA}汽车行驶时间 t(小时)
0
1
2
3
…
油箱剩余油量 Q(升)
100
94
88
82
…
5.为了解某种车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来,制成如表:
(1)根据上表可知,该车油箱的大小为 升,每小时耗油 升;
(2)请求出两个变量之间的关系式(用t来表示Q).
(3)当汽车行驶12小时,邮箱还剩多少升油?
解:(1)据上表可知,该车油箱的大小为100L,每小时耗油100-94=6 (L);
(2)由表格中的数据可得,Q=100-6t;
(3)令t=12,则Q=100-6×12=28(L)
6.一块长为5米,宽为2米的长方形木板,现要在长边上截取一边长为x米的一小长方形(如图),则剩余木板的面积y(平方米)与x(米)之间的关系式为 ( )
A.y=2x B.y=10-2x
C.y=5x D.y=10-5x
7. 用100 m长的篱笆在地上围成一个矩形,当矩形的宽由小到大变化时,矩形的面积也随之发生变化.
(1)在这个变化过程中,自变量、因变量各是什么?
(2)设矩形的宽为x(m),求矩形的面积y(m2)与x的关系式;
(3)当矩形的宽由1 m变化到25 m时,矩形面积由y1(m2)变化到y2(m2),求y1和y2的值.
解:(1)在这个变化过程中,自变量是矩形的宽,因变量是矩形的面积.
(3)当x=1时,y1=-12+50×1=49;
当x=25时,y2=-252+50×25=625.
(2)由题意,得y=x(?100?2-x)=-x2+50x.
?
8.如图,长方形ABCD的边长分别为AB=12cm,AD=8cm,点P、Q从点A出发,P沿线段AB运动,点Q沿线段AD运动(其中一点停止运动,另一点也随着停止),设AP=AQ=xcm在这个变化过程中,图中阴影部分的面积y(cm2)也随之变化.
(1)写出y与x的关系式.
(2)当AP由2cm变到8cm,图中阴影部分的面积y是如何变化的?请说明理由.
求变量之间关系式的“途径”
1.根据表格中所列的数据,归纳总结两个变量的关系式.
2.利用公式写出两个变量之间的关系式,比如各类
几何图形的周长、面积、体积公式等.
习题3.2
第1、2题
的变量间关系
学习目标
1)理解两个变量之间的关系可以用关系式表示,能在一个关系式中指出自变量和因变量。
2)能够在具体的情境中列出表示变量关系的关系式。
重点:能够在具体的情境中列出表示变量关系的关系式。
难点:能用适当的函数表示方法刻画简单实际问题中变量之间的关系。
在“小车下滑的时间”中,
1.支撑物的高度h和小车下滑的时间t都在变化,它们都是变量.其中小车下滑的时间t随支撑物的高度h的变化而变化,
2.支撑物的高度h是自变量,
3.小车下滑的时间t是因变量.
常量、变量、自变量、因变量:
2.在某一变化过程中,不断变化的量叫作变量.
3.如果一个变量y随另一个变量x的变化而变化,则把x叫作自变量 ,y叫作因变量.
1.在变化过程中数值始终不变的量叫做常量.
游戏:数青蛙
一只青蛙一张嘴,两只眼睛四条腿;
两只青蛙两张嘴,四只眼睛八条腿;
三只青蛙三张嘴,六只眼睛十二条腿;
……
1.青蛙的眼睛数和只数有关系吗?能用数学式表达吗?
2.青蛙的腿数和只数有关系吗?能用数学式表达吗?
这个游戏你能继续玩下去吗?
确定一个三角形面积的量有哪些?
D
B
C
A
三角形的底和高
用关系式表示变量间的关系
A
B
C
如图,△ABC底边BC上的高是6厘米。当三角形的顶点C沿底边所在的直线向B运动时,三角形的面积发生了怎样的变化?
(1)在这个变化过程中自
变量和因变量分别是什么?
三角形的底边长度是自变量
三角形的面积是因变量
高是常量,没有发生变化
A
B
C
A
B
C
三角形ABC的高为6cm
(2)如果三角形底边BC长为x(cm)。那么三角形的面积y(cm2)可以表示为 。
y=3x
A
B
C
三角形ABC的高为6cm
(3)当低边从12cm变化到3cm时,三角形的面积从 cm2 变化到 cm2
36
9
y=3x表示了 和 之间的关系,它是变量y随x变化的关系式。
三角形底边长
三角形面积
关系式是我们表示变量之间关系的另一种方法.
你能直观地表示这个关系式吗?
y=3x 表示了_________________和______之间的关系,它是变量_____随_____变化的关系式。
三角形底边边长 x
面积y
y
x
3x
含自变量代数式
因变量
系数为1
=
y
因变量要单独写在等式的左边
自变量x
关系式y=3x
因变量y
关系式是我们表示变量之间关系的另一种方法.
你还记得圆锥的体积公式是什么吗?
其中的字母表示什么?
如图,圆锥的高度是4厘米,当圆锥的底面半径由小到大变化时,圆锥的体积也随之发生了变化.
问题一 在这个变化过程中,自变量、因变量各是什么?
问题二 如果圆锥底面半径为 r(cm),那么圆锥的体积V(cm3)与r的关系式为________.
问题三 当底面半径由1cm变化到10cm时,圆锥的体积由 cm3变化到 cm3 .
圆锥的底面半径的长度是自变量,圆锥的体积是因变量。
V=43πr2
?
43π
?
4003π
?
例1.汽车在行驶过程中,由于惯性的作用刹车后仍将滑行一段距离才能停住,这段距离称为刹车距离.刹车距离是分析事故原因的一个重要因素.
某型号的汽车在平整路面上的刹车距离sm与车速vkm/h之间有下列经验公式:
(1)式中哪个量是常量?哪个量是变量?哪个量是自变量?哪个量是因变量?
(2)当刹车时车速v 分别是40、80、120km/h时,相应的滑行距离s分别是多少?
256 s,v v s.
当v=40km/h时, s=6.25m;
当 v=80km/h时, s=25m;
当 v=120km/h时,s=56.25m.
你知道什么是“低碳生活”吗?“低碳生活”是指人们生活中尽量减少所耗能量,从而降低碳、特别是二氧化碳的排放量的一种方式.
你知道什么是“低碳生活”吗?“低碳生活”是指人们生活中尽量减少所耗能量,从而降低碳、特别是二氧化碳的排放量的一种方式。
问题一 用字母表示家居用电的二氧化碳排放量的公式为_____________,其中的字母表示________________
______________________.
问题二 在上述关系式中,耗电量每增加 1 kW·h,二氧化碳排放量增加_________。当耗电量从 1 kW·h 增加到100 kW·h 时,二氧化碳排放量从________增加到____________。
问题三 小明家本月用电大约110 kW·h、天然气20m3、自来水5 t、油耗75 L,请你计算一下小明家这几项的二氧化碳排放量。
y = 0.785x
耗电量(x)和二氧化碳排放量(y)
0.785 kg
0.785 kg
78.5 kg
家居用电的二氧化碳:110×0.785=86.35(kg)
开私家车的二氧化碳:75×2.7=202.5(kg)
家用天然气的二氧化碳:20×0.19=3.8(kg)
家用自来水的二氧化碳:5×0.91=4.55(kg)
例2.某工厂现在年产值是15万元,计划今后每年增加2万元.
(1)年产值y(万元)与年数x之间的关系式为 __________;
(2)5年后的年产值是______万元.
解析:(1)根据题意可知,现在年产值是15万元,计划今后
每年增加2万元,x年后增加2x万元,所以年产值y(万元)与年数x之间的关系式为y=2x+15;
(2)将x=5代入关系式得:y=2x+15=2×5+15=25.
y=2x+15
25
1. 汽车在匀速行驶过程中,路程s、速度v和时间t之间的关系为s=vt,下列说法正确的是( )
A. s,v,t都是变量
B. s,t是变量,v是常量
C. v,t是变量,s是常量
D. s,v是变量,t是常量
B
2.变量x与y之间的关系式是y=x2-3,当自变量x=2时,因变量y的值是( )
A.-2 B.-1 C.1 D.2
3. 如果每盒笔售价16元,共有10支,用y(元)表示笔的售价,x(支)表示笔的数量,那么y与x的关系式为( )
A. y=10x B. y=16x
C. y=?8?5x D. y=?5?8x
?
C
4.百货大楼进了一批花布,出售时要在进价(进货价格)的基础上加一定的利润,其长度x与售价y如下表:
{5940675A-B579-460E-94D1-54222C63F5DA}长度x/m
1
2
3
4
…
售价y/元
8+0.3
16+0.6
24+0.9
32+1.2
…
下列用长度x表示售价y的关系式中,正确的是( )
A.y=8x+0.3 B.y=(8+0.3)x
C.y=8+0.3x D.y=8+0.3+x
{5940675A-B579-460E-94D1-54222C63F5DA}汽车行驶时间 t(小时)
0
1
2
3
…
油箱剩余油量 Q(升)
100
94
88
82
…
5.为了解某种车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来,制成如表:
(1)根据上表可知,该车油箱的大小为 升,每小时耗油 升;
(2)请求出两个变量之间的关系式(用t来表示Q).
(3)当汽车行驶12小时,邮箱还剩多少升油?
解:(1)据上表可知,该车油箱的大小为100L,每小时耗油100-94=6 (L);
(2)由表格中的数据可得,Q=100-6t;
(3)令t=12,则Q=100-6×12=28(L)
6.一块长为5米,宽为2米的长方形木板,现要在长边上截取一边长为x米的一小长方形(如图),则剩余木板的面积y(平方米)与x(米)之间的关系式为 ( )
A.y=2x B.y=10-2x
C.y=5x D.y=10-5x
7. 用100 m长的篱笆在地上围成一个矩形,当矩形的宽由小到大变化时,矩形的面积也随之发生变化.
(1)在这个变化过程中,自变量、因变量各是什么?
(2)设矩形的宽为x(m),求矩形的面积y(m2)与x的关系式;
(3)当矩形的宽由1 m变化到25 m时,矩形面积由y1(m2)变化到y2(m2),求y1和y2的值.
解:(1)在这个变化过程中,自变量是矩形的宽,因变量是矩形的面积.
(3)当x=1时,y1=-12+50×1=49;
当x=25时,y2=-252+50×25=625.
(2)由题意,得y=x(?100?2-x)=-x2+50x.
?
8.如图,长方形ABCD的边长分别为AB=12cm,AD=8cm,点P、Q从点A出发,P沿线段AB运动,点Q沿线段AD运动(其中一点停止运动,另一点也随着停止),设AP=AQ=xcm在这个变化过程中,图中阴影部分的面积y(cm2)也随之变化.
(1)写出y与x的关系式.
(2)当AP由2cm变到8cm,图中阴影部分的面积y是如何变化的?请说明理由.
求变量之间关系式的“途径”
1.根据表格中所列的数据,归纳总结两个变量的关系式.
2.利用公式写出两个变量之间的关系式,比如各类
几何图形的周长、面积、体积公式等.
习题3.2
第1、2题
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
