第11章 平面直角坐标系 复习课 沪科版八年级上册数学(22张PPT)
文档属性
| 名称 | 第11章 平面直角坐标系 复习课 沪科版八年级上册数学(22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 466.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 21:57:09 | ||
图片预览








文档简介
(共22张PPT)
第十一章 平面直角坐标系
复习课
1.能画出平面直角坐标系,会在直角坐标系中描点,能写出直角坐标系中点的坐标.
2.知道直角坐标系中的点与有序实数对的一一对应关系,体会数形结合的思想.
3.理解平面直角坐标系中图形的平移与坐标的变化规律.
一、学习目标
二、知识结构
一一对应
平面直角坐标系
概念及有关知识
坐标方法的应用
有序数对(a,b)
坐标系画法(坐标、x轴和y轴、象限)
平面上的点
点的坐标
表示地理位置
表示平移(点的平移、图形的平移)
三、知识梳理
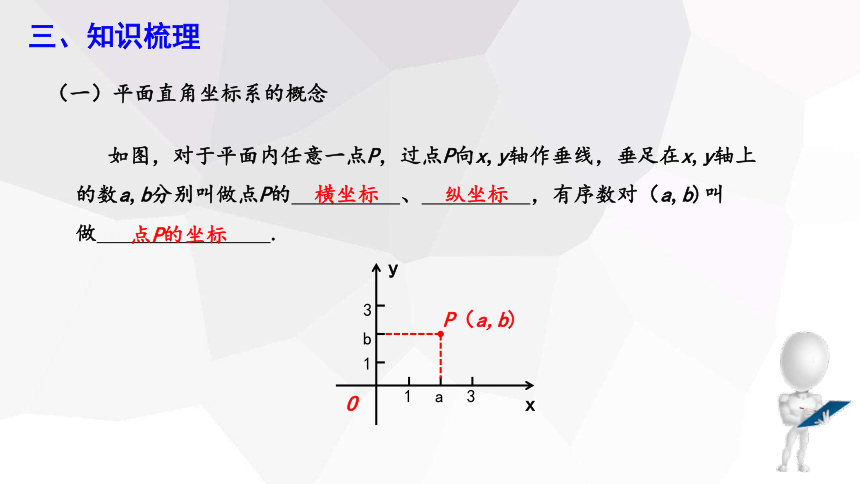
(一)平面直角坐标系的概念
在平面内画两条互相垂直并且原点重合的数轴,水平的数轴叫做 ,取向右为正方向;垂直的数轴叫做 ,取向上为正方向;两轴的交点O为原点.这样就建立了 ,这个平面叫做 .
横轴或x轴
纵轴或y轴
平面直角坐标系
坐标平面
三、知识梳理
(一)平面直角坐标系的概念
横坐标
如图,对于平面内任意一点P,过点P向x,y轴作垂线,垂足在x,y轴上的数a,b分别叫做点P的 、 ,有序数对(a,b)叫做 .
纵坐标
点P的坐标
1
a
3
1
b
3
O
x
y
P(a,b)
三、知识梳理
(二)象限及其坐标特点
第一象限
(1)两条坐标轴x与y将平面划分为四个部分.两条数轴正半轴所夹部分叫 ,其他三个部分按逆时针方向依次叫做 、
和 .坐标轴上的点不属于任何象限.
第二象限
第三象限
第四象限
(2)第一、二、三、四象限内的点的坐标符号分别是 、 、
、 .
(+,+)
(-,+)
(-,-)
(+,-)
三、知识梳理
(三)点的坐标与坐标轴的关系
|y|
(1)平面上有一点P的坐标是(x,y),这点P到坐标轴的距离为:
到x轴的距离为 ,到y轴的距离为 .
|x|
(2)如果x轴上有两点M(x1,0),N(x2,0)(x1x2-x1
y2-y1
三、知识梳理
(四)图形的平移
纵
在平面直角坐标系中,把图形向左(或右)平移a个单位长度,点的 坐标不变, 坐标减去(或加上)a;向上(或下)平移b个单位长度,点的 坐标不变, 坐标加上(或减去)b.
横
横
纵
四、典型例题
例1.如图是某市市区几个旅游景点的平面示意图,(1)选取某一景点为坐标原点,建立平面直角坐标系;(2)写出其余各景点的坐标。
动物园
山陕会馆
金凤广场
光岳楼
湖心岛
四、典型例题
解:(1)以金凤广场为坐标原点,如图:
动物园
山陕会馆
金凤广场
光岳楼
湖心岛
x
y
(2)金凤广场的坐标为(0,0);
湖心岛的坐标为(1,4);
光岳楼的坐标为(2,2);
山陕会馆的坐标为(4,1);
动物园的坐标为(6,6).
【当堂检测】
1.中国象棋是中华民族的文化瑰宝,因趣味性强,深受大众喜爱.如图,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点(0,-2),“马”位于点(4,-2),则“兵”位于点 .
(-1,1)
分析:如图所示,可得原点位置,则“兵”位于点(-1,1).
x
y
O
四、典型例题
例2.在平面直角坐标系中,已知点M(m,2m+3).
(1)若点M在x轴上,求x的值;
解:∵点M在x轴上,∴2m+3=0,
解得:m=-1.5,x=-1.5
四、典型例题
例2.在平面直角坐标系中,已知点M(m,2m+3).
(2)若点M在第二象限内,求m的取值范围;
解:∵点M在第二象限内,
∴
解得:-1.5<m<0
【当堂检测】
2.已知点P(x,y)位于第四象限,并且x≤y+4(x,y为整数),写出一个符合上述条件的点P的坐标 .
分析:∵点P(x,y)位于第四象限,并且x≤y+4(x,y为整数),
∴x>0,y<0,∴当x=1时,1≤y+4,
解得:0>y≥-3,
∴y可以为:-2,
故写一个符合上述条件的点的坐标可以为(1,-2)(答案不唯一).
(1,-2)
四、典型例题
例3.在平面直角坐标系中,描出下列3个点:A(-1,0),B(3,-1),C(4,3).
并顺次连接A、B、C,组成△ABC的,求△ABC的面积.
解:如图所示,
A
B
C
D
E
S△ABC=S梯形ADEC-S△ABD-S△BCE
=
=12.5-2-2
=8.5
答:△ABC的面积为8.5
连接ADEC,成一个梯形
【当堂检测】
3.已知点A(6,2),B(2,-4).求△AOB的面积(O为坐标原点)
解:如图所示,连接AOB,并在y轴上取点C、D,连接梯形ABCD
∴S△AOB=S梯形ABCD-S△AOD-S△BOC
C
D
x
y
O
2
4
2
4
-2
-4
-2
-4
A
B
6
=
=24-6-4
=14
答:△AOB的面积为14
四、典型例题
例4.如图,在方格纸中,每个小方格的边长均为1个长度单位,三角形ABC的三个顶点和点P都在小方格的顶点上,将三角形ABC平移,要求:①使点P落在平移后的三角形内部;②平移后的三角形的顶点在方格的顶点上.请你在图甲和图乙中画出符合上述要求的两个不同示意图,并写出平移的方法.
四、典型例题
解:如图:
图甲:先向右平移4个单位长度,再向上平移1个单位长度;
图乙:先向右平移3个单位长度,再向上平移1个单位长度;
【当堂检测】
4.已知点M(3,-2),将它先向左平移2个单位,再向上平移4个单位后得到点N,则点N的坐标是 .
分析:∵点M(3,-2),将它先向左平移2个单位,再向上平移4个单位后得到点N,
∴点N的坐标是(3-2,-2+4),即(1,2).
(1,2)
【当堂检测】
5.△ABC与△A'B'C'在平面直角坐标系中的位置如图
(1)分别写出下列各点的坐标:
A' ;B' ;C' .
(-3,-4)
(0,-1)
(2,-3)
【当堂检测】
5.△ABC与△A'B'C'在平面直角坐标系中的位置如图
(2)若点P(m,n)是△ABC内部一点,则平移后△A'B'C'内的对应点P'的坐标为 .
(m-4,n-4)
分析:A(1,0)变换到点A'的坐标是(-3,-4),横坐标减4,纵坐标减4,
∴点P的对应点P'的坐标是
(m-4,n-4).
五、课堂总结
第十一章 平面直角坐标系
复习课
1.能画出平面直角坐标系,会在直角坐标系中描点,能写出直角坐标系中点的坐标.
2.知道直角坐标系中的点与有序实数对的一一对应关系,体会数形结合的思想.
3.理解平面直角坐标系中图形的平移与坐标的变化规律.
一、学习目标
二、知识结构
一一对应
平面直角坐标系
概念及有关知识
坐标方法的应用
有序数对(a,b)
坐标系画法(坐标、x轴和y轴、象限)
平面上的点
点的坐标
表示地理位置
表示平移(点的平移、图形的平移)
三、知识梳理
(一)平面直角坐标系的概念
在平面内画两条互相垂直并且原点重合的数轴,水平的数轴叫做 ,取向右为正方向;垂直的数轴叫做 ,取向上为正方向;两轴的交点O为原点.这样就建立了 ,这个平面叫做 .
横轴或x轴
纵轴或y轴
平面直角坐标系
坐标平面
三、知识梳理
(一)平面直角坐标系的概念
横坐标
如图,对于平面内任意一点P,过点P向x,y轴作垂线,垂足在x,y轴上的数a,b分别叫做点P的 、 ,有序数对(a,b)叫做 .
纵坐标
点P的坐标
1
a
3
1
b
3
O
x
y
P(a,b)
三、知识梳理
(二)象限及其坐标特点
第一象限
(1)两条坐标轴x与y将平面划分为四个部分.两条数轴正半轴所夹部分叫 ,其他三个部分按逆时针方向依次叫做 、
和 .坐标轴上的点不属于任何象限.
第二象限
第三象限
第四象限
(2)第一、二、三、四象限内的点的坐标符号分别是 、 、
、 .
(+,+)
(-,+)
(-,-)
(+,-)
三、知识梳理
(三)点的坐标与坐标轴的关系
|y|
(1)平面上有一点P的坐标是(x,y),这点P到坐标轴的距离为:
到x轴的距离为 ,到y轴的距离为 .
|x|
(2)如果x轴上有两点M(x1,0),N(x2,0)(x1
y2-y1
三、知识梳理
(四)图形的平移
纵
在平面直角坐标系中,把图形向左(或右)平移a个单位长度,点的 坐标不变, 坐标减去(或加上)a;向上(或下)平移b个单位长度,点的 坐标不变, 坐标加上(或减去)b.
横
横
纵
四、典型例题
例1.如图是某市市区几个旅游景点的平面示意图,(1)选取某一景点为坐标原点,建立平面直角坐标系;(2)写出其余各景点的坐标。
动物园
山陕会馆
金凤广场
光岳楼
湖心岛
四、典型例题
解:(1)以金凤广场为坐标原点,如图:
动物园
山陕会馆
金凤广场
光岳楼
湖心岛
x
y
(2)金凤广场的坐标为(0,0);
湖心岛的坐标为(1,4);
光岳楼的坐标为(2,2);
山陕会馆的坐标为(4,1);
动物园的坐标为(6,6).
【当堂检测】
1.中国象棋是中华民族的文化瑰宝,因趣味性强,深受大众喜爱.如图,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点(0,-2),“马”位于点(4,-2),则“兵”位于点 .
(-1,1)
分析:如图所示,可得原点位置,则“兵”位于点(-1,1).
x
y
O
四、典型例题
例2.在平面直角坐标系中,已知点M(m,2m+3).
(1)若点M在x轴上,求x的值;
解:∵点M在x轴上,∴2m+3=0,
解得:m=-1.5,x=-1.5
四、典型例题
例2.在平面直角坐标系中,已知点M(m,2m+3).
(2)若点M在第二象限内,求m的取值范围;
解:∵点M在第二象限内,
∴
解得:-1.5<m<0
【当堂检测】
2.已知点P(x,y)位于第四象限,并且x≤y+4(x,y为整数),写出一个符合上述条件的点P的坐标 .
分析:∵点P(x,y)位于第四象限,并且x≤y+4(x,y为整数),
∴x>0,y<0,∴当x=1时,1≤y+4,
解得:0>y≥-3,
∴y可以为:-2,
故写一个符合上述条件的点的坐标可以为(1,-2)(答案不唯一).
(1,-2)
四、典型例题
例3.在平面直角坐标系中,描出下列3个点:A(-1,0),B(3,-1),C(4,3).
并顺次连接A、B、C,组成△ABC的,求△ABC的面积.
解:如图所示,
A
B
C
D
E
S△ABC=S梯形ADEC-S△ABD-S△BCE
=
=12.5-2-2
=8.5
答:△ABC的面积为8.5
连接ADEC,成一个梯形
【当堂检测】
3.已知点A(6,2),B(2,-4).求△AOB的面积(O为坐标原点)
解:如图所示,连接AOB,并在y轴上取点C、D,连接梯形ABCD
∴S△AOB=S梯形ABCD-S△AOD-S△BOC
C
D
x
y
O
2
4
2
4
-2
-4
-2
-4
A
B
6
=
=24-6-4
=14
答:△AOB的面积为14
四、典型例题
例4.如图,在方格纸中,每个小方格的边长均为1个长度单位,三角形ABC的三个顶点和点P都在小方格的顶点上,将三角形ABC平移,要求:①使点P落在平移后的三角形内部;②平移后的三角形的顶点在方格的顶点上.请你在图甲和图乙中画出符合上述要求的两个不同示意图,并写出平移的方法.
四、典型例题
解:如图:
图甲:先向右平移4个单位长度,再向上平移1个单位长度;
图乙:先向右平移3个单位长度,再向上平移1个单位长度;
【当堂检测】
4.已知点M(3,-2),将它先向左平移2个单位,再向上平移4个单位后得到点N,则点N的坐标是 .
分析:∵点M(3,-2),将它先向左平移2个单位,再向上平移4个单位后得到点N,
∴点N的坐标是(3-2,-2+4),即(1,2).
(1,2)
【当堂检测】
5.△ABC与△A'B'C'在平面直角坐标系中的位置如图
(1)分别写出下列各点的坐标:
A' ;B' ;C' .
(-3,-4)
(0,-1)
(2,-3)
【当堂检测】
5.△ABC与△A'B'C'在平面直角坐标系中的位置如图
(2)若点P(m,n)是△ABC内部一点,则平移后△A'B'C'内的对应点P'的坐标为 .
(m-4,n-4)
分析:A(1,0)变换到点A'的坐标是(-3,-4),横坐标减4,纵坐标减4,
∴点P的对应点P'的坐标是
(m-4,n-4).
五、课堂总结
