第十七章 勾股定理 单元复习 课件 人教版数学八年级下册(23张PPT)
文档属性
| 名称 | 第十七章 勾股定理 单元复习 课件 人教版数学八年级下册(23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 454.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 21:58:34 | ||
图片预览



文档简介
(共23张PPT)
章末复习
R·八年级数学下册
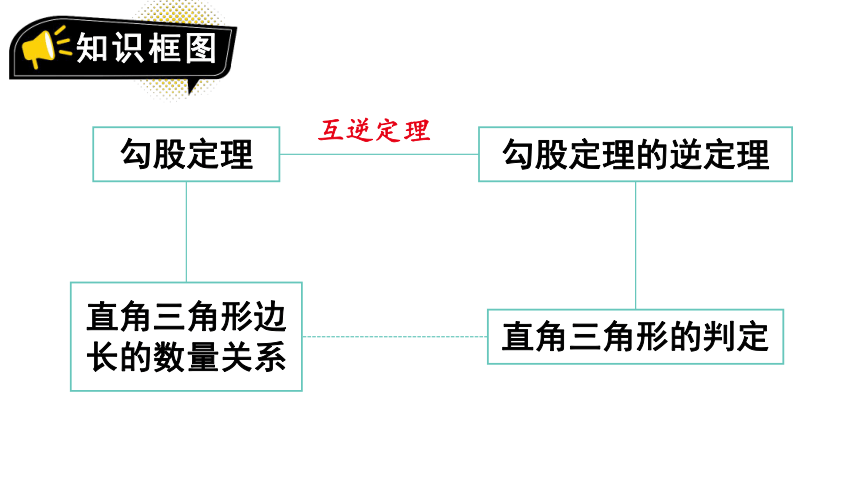
勾股定理
勾股定理的逆定理
直角三角形边长的数量关系
直角三角形的判定
互逆定理
知识框图
复习回顾
回顾思考:
1.直角三角形三边的长有什么特殊的关系
2.赵爽证明勾股定理运用了什么思想方法
3.已知一个三角形的三边长,怎样判断它是不是直角三角形 你作判断的依据是什么
4.证明勾股定理的逆定理运用了什么方法
5.一个命题成立,它的逆命题未必成立. 请举例说明.
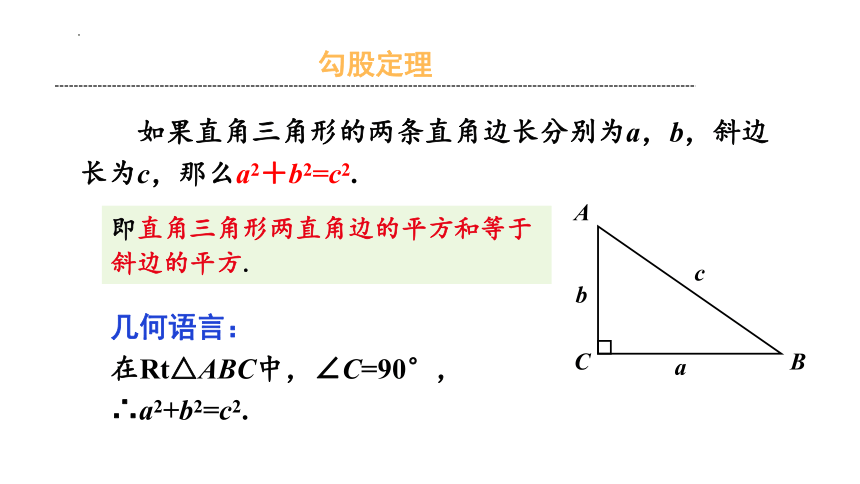
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
A
C
B
b
a
c
即直角三角形两直角边的平方和等于斜边的平方.
几何语言:
在Rt△ABC中,∠C=90°,
∴a2+b2=c2.
勾股定理
例1 在Rt△ABC中,已知两直角边分别是5和12,则第三边长度为______.
例2 若直角三角形的两边的长分别为 和2,则该直角三角形第三边长为________.
13
1或
①已知两边,求第三边
典型例题
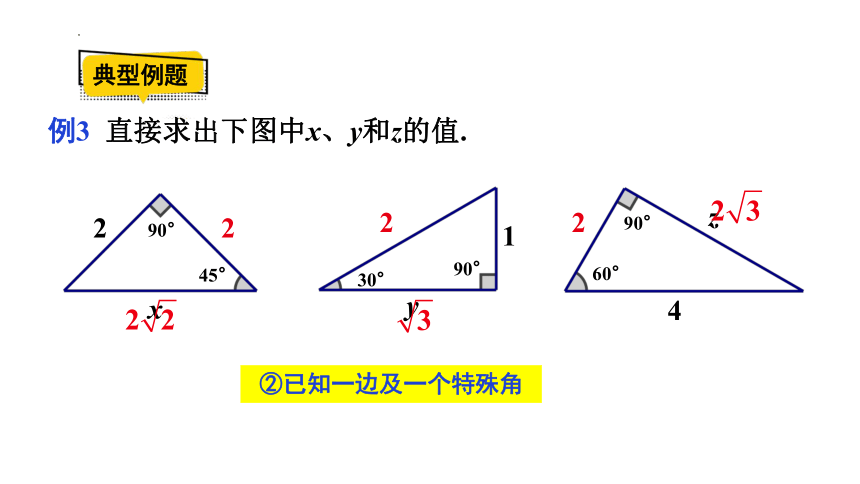
例3 直接求出下图中x、y和z的值.
2
x
y
1
4
z
90°
90°
90°
45°
30°
60°
2
2
2
②已知一边及一个特殊角
典型例题
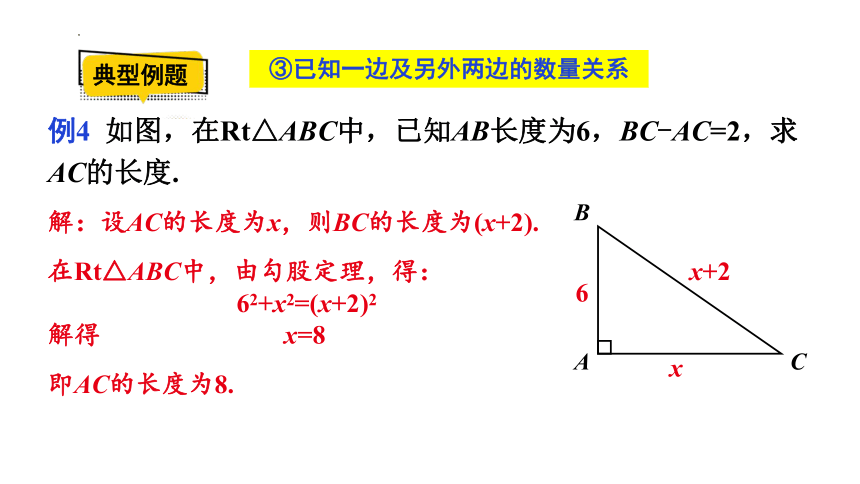
例4 如图,在Rt△ABC中,已知AB长度为6,BC-AC=2,求AC的长度.
B
A
C
解:设AC的长度为x,则BC的长度为(x+2).
在Rt△ABC中,由勾股定理,得:
62+x2=(x+2)2
解得 x=8
即AC的长度为8.
③已知一边及另外两边的数量关系
6
x+2
x
典型例题
勾股定理的证明
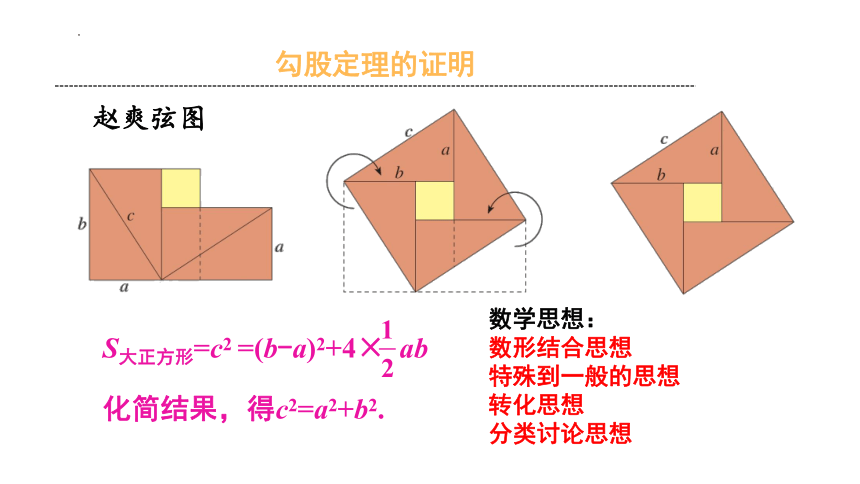
赵爽弦图
S大正方形=c2
=(b-a)2+4× ab
化简结果,得c2=a2+b2.
数学思想:
数形结合思想
特殊到一般的思想
转化思想
分类讨论思想
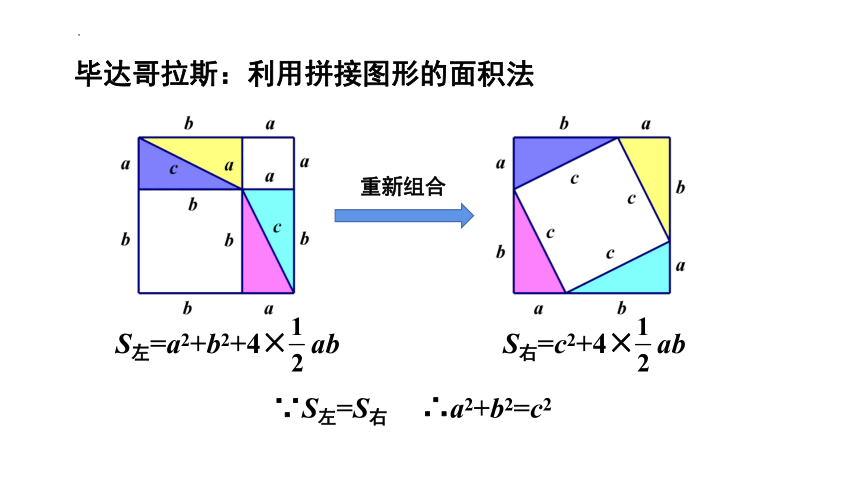
毕达哥拉斯:利用拼接图形的面积法
重新组合
S左=a2+b2+4× ab
S右=c2+4× ab
∵S左=S右
∴a2+b2=c2
加菲尔德:梯形面积法
题设:Rt△ABC≌Rt△CDE
易证:△ACE为直角三角形,四边形ABDE为梯形
S梯形ABDE=S△ABC+S△CDE+S△ACE
即 (a+b)(a+b)= ×2×ab+ c2
化简得:a2+b2=c2
达芬奇证明方法:
思考:如何判定一个三角形是直角三角形呢?
1.有一个内角为直角的三角形是直角三角形.
2.两个内角互余的三角形是直角三角形.
3.如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
A
C
B
b
a
c
勾股定理的逆定理
几何语言:∵a2+b2=c2,
∴△ABC是直角三角形.
例5 试判断下列边长组成的三角形是否为直角三角形:
(1)a=2,b=3,c=4;
(2)a=6,b=8,c=10;
(3)a=5,b=13,c=17.
22+32≠42,不是直角三角形.
62+82=102,是直角三角形.
52+132≠172,不是直角三角形.
像这样,能成为直角三角形三条边长的正整数,称为勾股数.
典型例题
例6 如图,一块铁皮(图中阴影部分),测得AB=3,BC=4,CD=13,AD=12,∠B=90°﹒求阴影部分的面积.
又∵AC2+AD2=52+122=169=132,
∴AC2+AD2=CD2,
∴△ACD是直角三角形,
∠CAD=90°.
S阴影=S△CAD-S△ABC
= AC·AD- AB·BC
=24
解:如图,连接AC.
∠B=90°,AB=3,BC=4,由勾股定理得:
AC= =5.
典型例题
勾股定理
题设:一个三角形是直角三角形.
结论:两条直角边的平方和等于斜边的平方.
(a2+b2=c2)
勾股定理
的逆定理
题设:一个三角形的三边长a,b,c满足a2+b2=c2.
结论:这个三角形是直角三角形.
若两个命题的题设、结论正好相反,则这两个命题叫做互逆命题.
互逆命题
题设:一个三角形是直角三角形.
结论:两条直角边的平方和等于斜边的平方.
(a2+b2=c2)
题设:一个三角形的三边长a,b,c满足a2+b2=c2.
结论:这个三角形是直角三角形.
如果把其中一个叫原命题,那么另一个叫做它的逆命题.
如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,称这两个定理互为逆定理.
思考:一个命题成立,它的逆命题一定成立吗?请举例说明.
原命题:如果两个角是直角,那么它们相等.
逆命题:如果两个角相等,那么这两个角是直角.
该逆命题不成立.
例7 下列命题中,逆命题仍然成立的是( ).
A.全等三角形的面积相等
B.到角两边距离相等的点在这个角的平分线上
C.同一个角的余角相等
D.等腰三角形是轴对称图形
B
典型例题
1.如图,一个圆柱形油罐,要从A点环绕油罐建梯子,正好到A点的正上方B点,请你算一算梯子最短需多少米?(已知油罐的底面周长是12米,高是5米).
解:如图,将油罐侧面展开,
此时AB= =13(m).
巩固练习
2.如图,已知在△ABC中,AB=17,AC=10,BC边上的高AD=8,求:(1)BC边的长;(2)△ABC的面积.
解:(1)∵AD⊥BC,AB=17,AC=10,AD=8,
在Rt△ABD中,由勾股定理,得:
BD2= =15.
在Rt△ACD中,由勾股定理,得:
CD2= =6.
∴BC=BD+CD=21.
(2)S△ABC= AD·BC=84.
3.如图,一块直角三角形的纸片,两直角AC=6,BC=8.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长.
解:由折叠可知AC=AE=6.
在Rt△ACB中,AC=6,CB=8,由勾股定理得AB= =10. ∴EB=4.
设CD长为x,则BD=(8-x).
Rt△BDE中,由勾股定理,得
(8-x)2=x2+42,解得x=3.
4.如图是一个三级台阶,它的每一级的长、宽和高分别为9,3和1,A和B是这个台阶两个相对的端点,A处有一只蚂蚁,想到B处去吃可口的食物,则这只蚂蚁沿着台阶面爬行的最短路程是多少?
9
A
B
3
1
3
1
3
1
C
提示:AB2=AC2+BC2
直角三角形
勾股定理
勾股定理的逆定理
互逆命题、互逆定理
勾股定理的证明——赵爽弦图
应 用
课堂小结
章末复习
R·八年级数学下册
勾股定理
勾股定理的逆定理
直角三角形边长的数量关系
直角三角形的判定
互逆定理
知识框图
复习回顾
回顾思考:
1.直角三角形三边的长有什么特殊的关系
2.赵爽证明勾股定理运用了什么思想方法
3.已知一个三角形的三边长,怎样判断它是不是直角三角形 你作判断的依据是什么
4.证明勾股定理的逆定理运用了什么方法
5.一个命题成立,它的逆命题未必成立. 请举例说明.
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
A
C
B
b
a
c
即直角三角形两直角边的平方和等于斜边的平方.
几何语言:
在Rt△ABC中,∠C=90°,
∴a2+b2=c2.
勾股定理
例1 在Rt△ABC中,已知两直角边分别是5和12,则第三边长度为______.
例2 若直角三角形的两边的长分别为 和2,则该直角三角形第三边长为________.
13
1或
①已知两边,求第三边
典型例题
例3 直接求出下图中x、y和z的值.
2
x
y
1
4
z
90°
90°
90°
45°
30°
60°
2
2
2
②已知一边及一个特殊角
典型例题
例4 如图,在Rt△ABC中,已知AB长度为6,BC-AC=2,求AC的长度.
B
A
C
解:设AC的长度为x,则BC的长度为(x+2).
在Rt△ABC中,由勾股定理,得:
62+x2=(x+2)2
解得 x=8
即AC的长度为8.
③已知一边及另外两边的数量关系
6
x+2
x
典型例题
勾股定理的证明
赵爽弦图
S大正方形=c2
=(b-a)2+4× ab
化简结果,得c2=a2+b2.
数学思想:
数形结合思想
特殊到一般的思想
转化思想
分类讨论思想
毕达哥拉斯:利用拼接图形的面积法
重新组合
S左=a2+b2+4× ab
S右=c2+4× ab
∵S左=S右
∴a2+b2=c2
加菲尔德:梯形面积法
题设:Rt△ABC≌Rt△CDE
易证:△ACE为直角三角形,四边形ABDE为梯形
S梯形ABDE=S△ABC+S△CDE+S△ACE
即 (a+b)(a+b)= ×2×ab+ c2
化简得:a2+b2=c2
达芬奇证明方法:
思考:如何判定一个三角形是直角三角形呢?
1.有一个内角为直角的三角形是直角三角形.
2.两个内角互余的三角形是直角三角形.
3.如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
A
C
B
b
a
c
勾股定理的逆定理
几何语言:∵a2+b2=c2,
∴△ABC是直角三角形.
例5 试判断下列边长组成的三角形是否为直角三角形:
(1)a=2,b=3,c=4;
(2)a=6,b=8,c=10;
(3)a=5,b=13,c=17.
22+32≠42,不是直角三角形.
62+82=102,是直角三角形.
52+132≠172,不是直角三角形.
像这样,能成为直角三角形三条边长的正整数,称为勾股数.
典型例题
例6 如图,一块铁皮(图中阴影部分),测得AB=3,BC=4,CD=13,AD=12,∠B=90°﹒求阴影部分的面积.
又∵AC2+AD2=52+122=169=132,
∴AC2+AD2=CD2,
∴△ACD是直角三角形,
∠CAD=90°.
S阴影=S△CAD-S△ABC
= AC·AD- AB·BC
=24
解:如图,连接AC.
∠B=90°,AB=3,BC=4,由勾股定理得:
AC= =5.
典型例题
勾股定理
题设:一个三角形是直角三角形.
结论:两条直角边的平方和等于斜边的平方.
(a2+b2=c2)
勾股定理
的逆定理
题设:一个三角形的三边长a,b,c满足a2+b2=c2.
结论:这个三角形是直角三角形.
若两个命题的题设、结论正好相反,则这两个命题叫做互逆命题.
互逆命题
题设:一个三角形是直角三角形.
结论:两条直角边的平方和等于斜边的平方.
(a2+b2=c2)
题设:一个三角形的三边长a,b,c满足a2+b2=c2.
结论:这个三角形是直角三角形.
如果把其中一个叫原命题,那么另一个叫做它的逆命题.
如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,称这两个定理互为逆定理.
思考:一个命题成立,它的逆命题一定成立吗?请举例说明.
原命题:如果两个角是直角,那么它们相等.
逆命题:如果两个角相等,那么这两个角是直角.
该逆命题不成立.
例7 下列命题中,逆命题仍然成立的是( ).
A.全等三角形的面积相等
B.到角两边距离相等的点在这个角的平分线上
C.同一个角的余角相等
D.等腰三角形是轴对称图形
B
典型例题
1.如图,一个圆柱形油罐,要从A点环绕油罐建梯子,正好到A点的正上方B点,请你算一算梯子最短需多少米?(已知油罐的底面周长是12米,高是5米).
解:如图,将油罐侧面展开,
此时AB= =13(m).
巩固练习
2.如图,已知在△ABC中,AB=17,AC=10,BC边上的高AD=8,求:(1)BC边的长;(2)△ABC的面积.
解:(1)∵AD⊥BC,AB=17,AC=10,AD=8,
在Rt△ABD中,由勾股定理,得:
BD2= =15.
在Rt△ACD中,由勾股定理,得:
CD2= =6.
∴BC=BD+CD=21.
(2)S△ABC= AD·BC=84.
3.如图,一块直角三角形的纸片,两直角AC=6,BC=8.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长.
解:由折叠可知AC=AE=6.
在Rt△ACB中,AC=6,CB=8,由勾股定理得AB= =10. ∴EB=4.
设CD长为x,则BD=(8-x).
Rt△BDE中,由勾股定理,得
(8-x)2=x2+42,解得x=3.
4.如图是一个三级台阶,它的每一级的长、宽和高分别为9,3和1,A和B是这个台阶两个相对的端点,A处有一只蚂蚁,想到B处去吃可口的食物,则这只蚂蚁沿着台阶面爬行的最短路程是多少?
9
A
B
3
1
3
1
3
1
C
提示:AB2=AC2+BC2
直角三角形
勾股定理
勾股定理的逆定理
互逆命题、互逆定理
勾股定理的证明——赵爽弦图
应 用
课堂小结
