等腰三角形的性质 课件 鲁教版数学七年级下册(32张PPT)
文档属性
| 名称 | 等腰三角形的性质 课件 鲁教版数学七年级下册(32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 00:00:00 | ||
图片预览










文档简介
(共32张PPT)
简单的轴对称图形
——等腰三角形
.
.
情景导入
.
.
.
.
生活中的等腰三角形
学习目标
1、掌握等腰三角形、等边三角形性质的应用;
2、理解等腰三角形的性质并会用符号语言表示;
3、认识等边三角形的轴对称性及性质
A
C
D
B
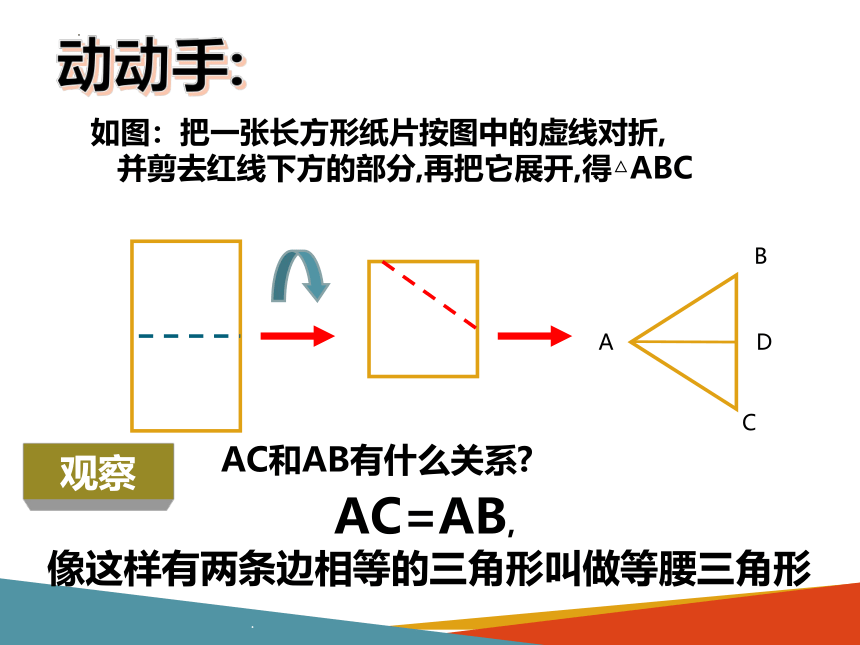
动动手:
观察
AC和AB有什么关系
AC=AB,
像这样有两条边相等的三角形叫做等腰三角形
.
如图:把一张长方形纸片按图中的虚线对折,
并剪去红线下方的部分,再把它展开,得△ABC
A
C
B
底角
底角
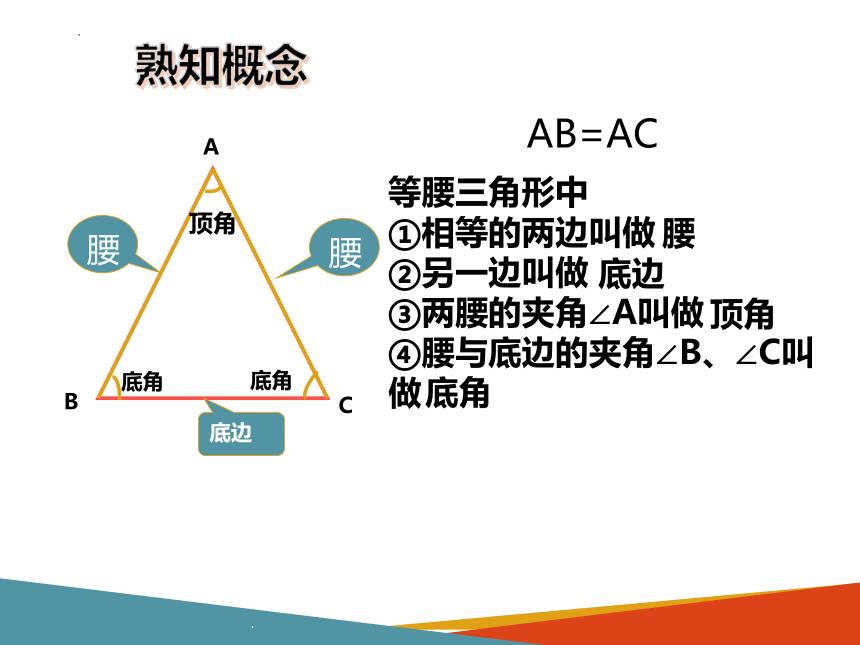
熟知概念
等腰三角形中
①相等的两边叫做
②另一边叫做
③两腰的夹角∠A叫做
④腰与底边的夹角∠B、∠C叫做
AB=AC
.
腰
腰
腰
底边
底边
顶角
顶角
底角
探索新知
重合的线段 重合的角
A
B
D
C
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠BAD = ∠CAD
∠ADB =∠ADC
.
将等腰三角形ABC纸板沿折痕对折,找出其中重合的线段和角
探索新知
等腰三角形是轴对称图形吗?如果是,请画出它的对称轴。
D
A
B
C
等腰三角形是轴对称图形。
如何用文字语言描述等腰三角形的对称轴?
探索新知
等腰三角形的顶角的平分线、底边上的中线、底边上的高
重合(也称为“三线合一)
它们所在的直线都是等腰三角形的对称轴。
A
B
C
D
A
B
C
D
知一线得二线
“三线合一”可以帮助我们解决线段的垂直、相等以及角的相等问题。
几何语言:
.
合作交流归纳新知
(1)∵ AB=BC,AD平分∠BAC
∴ BD=CD,AD⊥BC
(2)∵ AB=BC,BD=CD
∴ AD平分∠BAC,AD⊥BC
(3)∵ AB=BC,AD⊥BC
∴ BD=CD,AD平分∠BAC
A
B
C
D
.
例题:如图,在△ABC中,AB=AC,AD是∠BAC的角平分线,其中BD=4cm,求CD的长.
解:在△ABC中
∵ AB=BC,
AD是∠BAC的角平分线
∴ BD=CD=4cm
A
B
C
D
.
三线合一
重合
A
B
C
.
猜想
等腰三角形的两个底角有什么关系?
相等
提示:构造两个全等的三角形
A
B
C
则有∠1=∠2
D
1
2
在△ABD和△ACD中
AB=AC
∠1=∠2
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SAS)
∴ ∠B=∠C
(全等三角形对应角相等)
方法一:
做顶角∠BAC的平分线AD
已知:△ABC中,AB=AC求证:∠B= C
证明:
.
作底边BC边上的中线AD
在△ABD与△ACD中:
AB=AC(已知)
则有BD=CD
AD=AD(公共边)
∴△ABD≌△ACD(SSS)
∴∠B=∠C(全等三角形对应角相等)
A
B
C
D
BD=CD
方法二:
已知:△ABC中,AB=AC 求证:∠B= C
.
等腰三角形的两个底角相等。
(简写成“等边对等角”)
几何语言:
在△ABC中,
∵AB=AC
∴∠B= C(等边对等角)
等腰三角形的性质有哪些
性质3:等腰三角形两个底角相等(等边对等角)
性质2:等腰三角形的顶角的平分线、底边上的中线、底边上的高重合(也称为“三线合一“),它们所在的直线都是等腰三角形的对称轴。
归纳总结:
.
性质1:等腰三角形是轴对称图形
A
B
C
.
再探新知
三边都相等的三角形是等边三角形,也叫正三角形。
等边三角形有几条对称轴?
等边三角形是轴对称图形,有3条对称轴;等边三角形的顶角的平分线、底边上的中线、底边上的高重合(三线合一)
A
B
C
.
再探新知
等边三角形的角有什么性质?
等边三角形的内角都相等,都等于600.
1、等腰三角形一个角为120°,它的另外两个角为 ;
.
当堂检测
30°、30°
A
B
C
120°
2、等腰三角形一个角为70°,它的另外两个角为___________________;
70°,40°或 55°,55°
70°
55°
55°
70°
70°
40°
.
当堂检测
分类讨论思想
3、如图,在△ABC中,AB=AC,D为BC的中点,
∠BAD=350,则∠DAC的度数为( )
A.350 B.450
C.550 D.600
.
当堂检测
A
B
C
D
A
4.判断正误:在△ABC中,
∴ ∠B=∠C.
∵ AB=BC,
C
A
B
注意使用“等边对等角”时,
边与角的对应关系.
.
当堂检测
5.如图所示的三角形测平架中,AB=AC,在
BC的中点D挂一个重锤,自然下垂,使点A
恰好落在重锤线上,请问此时BC是否正好处于
水平位置?为什么?
.
应用生活
.
应用生活
课堂小结:
底边
A
C
B
腰
腰
顶角
底角
底角
说一说,这节课你学到了哪些知识?
.
1、等腰三角形的有关概念
两个底角相等,简称“等边对等角”
底边上的高、中线及顶角的平分线互相重合,简称“三线合一”
等腰三角形
3、能根据等腰三角形的概念与性质求等腰三角形的周长或知道一角求其它两角或证明线段、角相等。
2、等腰三角形的性质
.
是轴对称图形
作业:1、练习册P41、P42
2、学有余力同学做P42
课堂延伸
谢谢大家
简单的轴对称图形
——等腰三角形
.
.
情景导入
.
.
.
.
生活中的等腰三角形
学习目标
1、掌握等腰三角形、等边三角形性质的应用;
2、理解等腰三角形的性质并会用符号语言表示;
3、认识等边三角形的轴对称性及性质
A
C
D
B
动动手:
观察
AC和AB有什么关系
AC=AB,
像这样有两条边相等的三角形叫做等腰三角形
.
如图:把一张长方形纸片按图中的虚线对折,
并剪去红线下方的部分,再把它展开,得△ABC
A
C
B
底角
底角
熟知概念
等腰三角形中
①相等的两边叫做
②另一边叫做
③两腰的夹角∠A叫做
④腰与底边的夹角∠B、∠C叫做
AB=AC
.
腰
腰
腰
底边
底边
顶角
顶角
底角
探索新知
重合的线段 重合的角
A
B
D
C
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠BAD = ∠CAD
∠ADB =∠ADC
.
将等腰三角形ABC纸板沿折痕对折,找出其中重合的线段和角
探索新知
等腰三角形是轴对称图形吗?如果是,请画出它的对称轴。
D
A
B
C
等腰三角形是轴对称图形。
如何用文字语言描述等腰三角形的对称轴?
探索新知
等腰三角形的顶角的平分线、底边上的中线、底边上的高
重合(也称为“三线合一)
它们所在的直线都是等腰三角形的对称轴。
A
B
C
D
A
B
C
D
知一线得二线
“三线合一”可以帮助我们解决线段的垂直、相等以及角的相等问题。
几何语言:
.
合作交流归纳新知
(1)∵ AB=BC,AD平分∠BAC
∴ BD=CD,AD⊥BC
(2)∵ AB=BC,BD=CD
∴ AD平分∠BAC,AD⊥BC
(3)∵ AB=BC,AD⊥BC
∴ BD=CD,AD平分∠BAC
A
B
C
D
.
例题:如图,在△ABC中,AB=AC,AD是∠BAC的角平分线,其中BD=4cm,求CD的长.
解:在△ABC中
∵ AB=BC,
AD是∠BAC的角平分线
∴ BD=CD=4cm
A
B
C
D
.
三线合一
重合
A
B
C
.
猜想
等腰三角形的两个底角有什么关系?
相等
提示:构造两个全等的三角形
A
B
C
则有∠1=∠2
D
1
2
在△ABD和△ACD中
AB=AC
∠1=∠2
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SAS)
∴ ∠B=∠C
(全等三角形对应角相等)
方法一:
做顶角∠BAC的平分线AD
已知:△ABC中,AB=AC求证:∠B= C
证明:
.
作底边BC边上的中线AD
在△ABD与△ACD中:
AB=AC(已知)
则有BD=CD
AD=AD(公共边)
∴△ABD≌△ACD(SSS)
∴∠B=∠C(全等三角形对应角相等)
A
B
C
D
BD=CD
方法二:
已知:△ABC中,AB=AC 求证:∠B= C
.
等腰三角形的两个底角相等。
(简写成“等边对等角”)
几何语言:
在△ABC中,
∵AB=AC
∴∠B= C(等边对等角)
等腰三角形的性质有哪些
性质3:等腰三角形两个底角相等(等边对等角)
性质2:等腰三角形的顶角的平分线、底边上的中线、底边上的高重合(也称为“三线合一“),它们所在的直线都是等腰三角形的对称轴。
归纳总结:
.
性质1:等腰三角形是轴对称图形
A
B
C
.
再探新知
三边都相等的三角形是等边三角形,也叫正三角形。
等边三角形有几条对称轴?
等边三角形是轴对称图形,有3条对称轴;等边三角形的顶角的平分线、底边上的中线、底边上的高重合(三线合一)
A
B
C
.
再探新知
等边三角形的角有什么性质?
等边三角形的内角都相等,都等于600.
1、等腰三角形一个角为120°,它的另外两个角为 ;
.
当堂检测
30°、30°
A
B
C
120°
2、等腰三角形一个角为70°,它的另外两个角为___________________;
70°,40°或 55°,55°
70°
55°
55°
70°
70°
40°
.
当堂检测
分类讨论思想
3、如图,在△ABC中,AB=AC,D为BC的中点,
∠BAD=350,则∠DAC的度数为( )
A.350 B.450
C.550 D.600
.
当堂检测
A
B
C
D
A
4.判断正误:在△ABC中,
∴ ∠B=∠C.
∵ AB=BC,
C
A
B
注意使用“等边对等角”时,
边与角的对应关系.
.
当堂检测
5.如图所示的三角形测平架中,AB=AC,在
BC的中点D挂一个重锤,自然下垂,使点A
恰好落在重锤线上,请问此时BC是否正好处于
水平位置?为什么?
.
应用生活
.
应用生活
课堂小结:
底边
A
C
B
腰
腰
顶角
底角
底角
说一说,这节课你学到了哪些知识?
.
1、等腰三角形的有关概念
两个底角相等,简称“等边对等角”
底边上的高、中线及顶角的平分线互相重合,简称“三线合一”
等腰三角形
3、能根据等腰三角形的概念与性质求等腰三角形的周长或知道一角求其它两角或证明线段、角相等。
2、等腰三角形的性质
.
是轴对称图形
作业:1、练习册P41、P42
2、学有余力同学做P42
课堂延伸
谢谢大家
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
