18.2.1 矩形 第1课时 矩形的性质 课件 人教版数学八年级下册(31张PPT)
文档属性
| 名称 | 18.2.1 矩形 第1课时 矩形的性质 课件 人教版数学八年级下册(31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 22:02:39 | ||
图片预览





文档简介
(共31张PPT)
第十八章 平行四边形
矩形的性质
情境导入
拿一个活动的平行四边形教具,轻轻拉动一个点,它还是平行四边形吗 使一个角是直角,这时它是什么图形
点击查看平行四边形到矩形的变化过程
平行四边形
一个角是直角
矩形的概念:有一个角是直角的平行四边形叫做矩形,也就是长方形.
仔细观察下列实际生活中的图片,你觉得哪些是矩形的形象
矩形是生活中很常见的图形,你还能列举出矩形在生活中应用的其他例子吗
我们一起来探讨一下矩形的性质吧!
探索新知
探究点1:矩形的性质
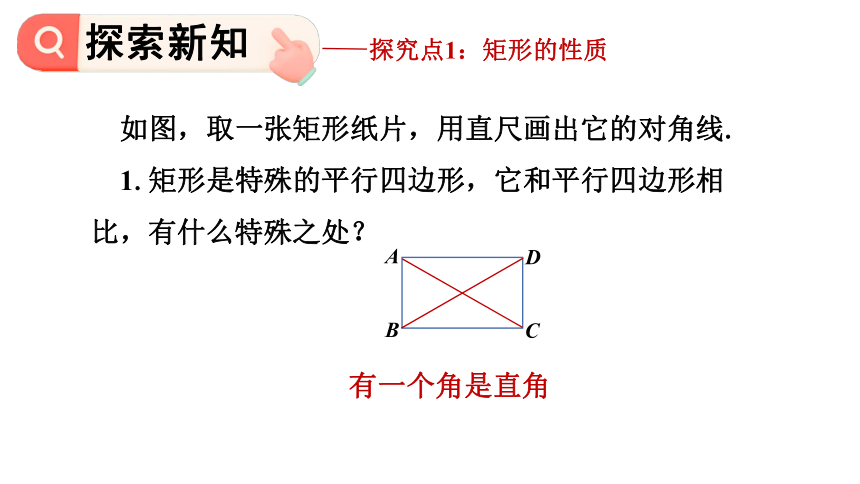
如图,取一张矩形纸片,用直尺画出它的对角线.
1.矩形是特殊的平行四边形,它和平行四边形相比,有什么特殊之处?
A
B
C
D
有一个角是直角
探索新知
探究点1:矩形的性质
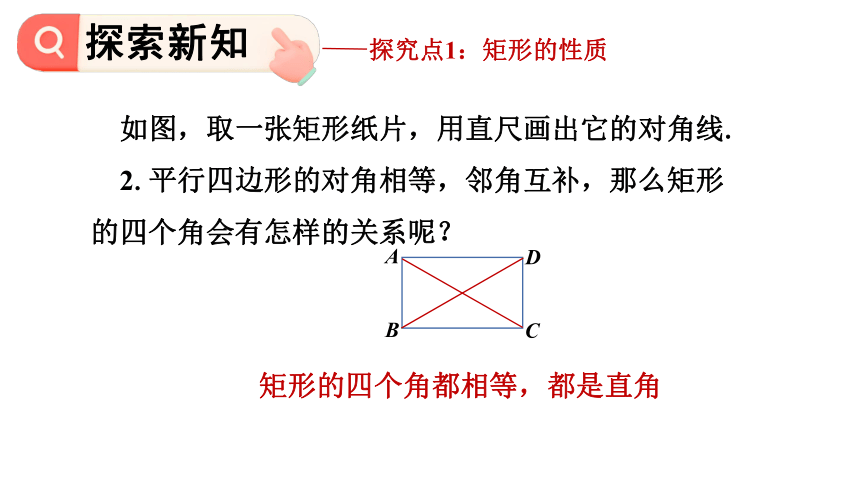
如图,取一张矩形纸片,用直尺画出它的对角线.
2.平行四边形的对角相等,邻角互补,那么矩形的四个角会有怎样的关系呢?
A
B
C
D
矩形的四个角都相等,都是直角
探索新知
探究点1:矩形的性质
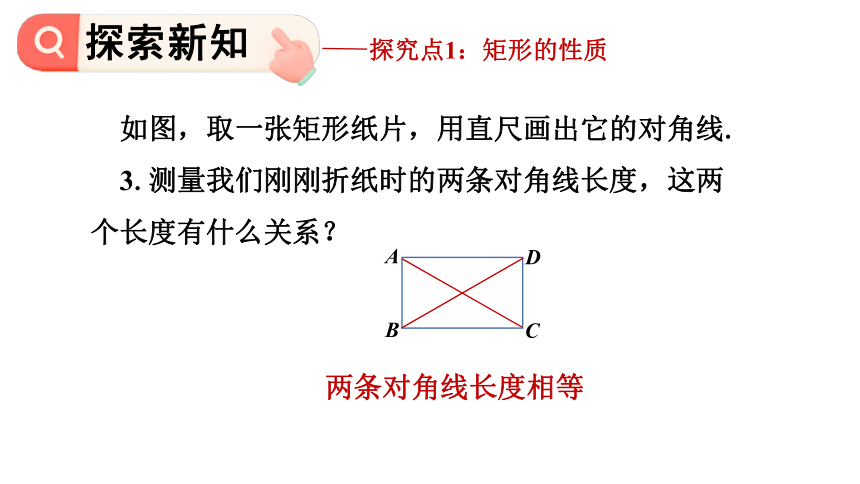
如图,取一张矩形纸片,用直尺画出它的对角线.
3.测量我们刚刚折纸时的两条对角线长度,这两个长度有什么关系?
A
B
C
D
两条对角线长度相等
探索新知
探究点1:矩形的性质
1.如图,在矩形ABCD中,∠A=90°,
求证:∠A=∠B=∠C=∠D=90°.
∴AB∥CD, ∠A=∠C.
证明:∵矩形 ABCD 是特殊的平行四边形,
同理:∠B=90°.∴∠A=∠B=∠C=∠D=90°.
∵∠A=90°,
∴∠C=90°,∠D=180°-90°=90°.
D
A
B
C
下面我们来一起验证一下:
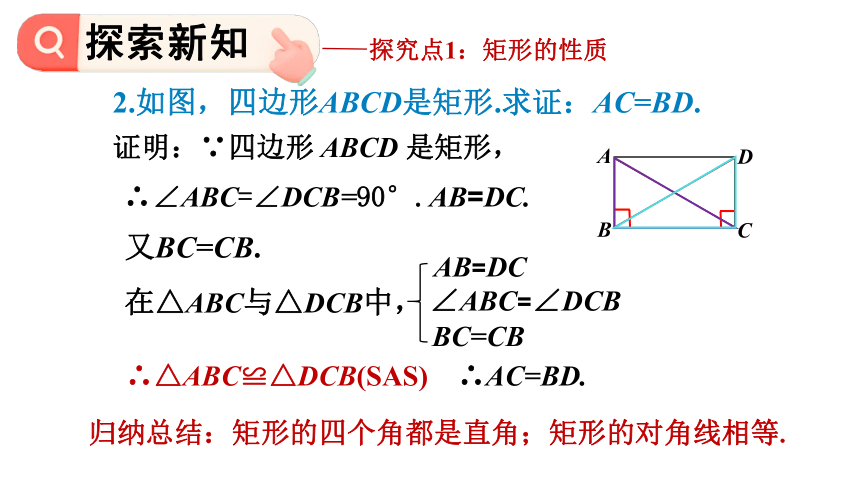
2.如图,四边形ABCD是矩形.求证:AC=BD.
探索新知
探究点1:矩形的性质
A
B
C
D
∴∠ABC=∠DCB=90°.AB=DC.
证明:∵四边形 ABCD 是矩形,
又BC=CB.
在△ABC与△DCB中,
AB=DC
∠ABC=∠DCB
BC=CB
∴△ABC≌△DCB(SAS) ∴AC=BD.
归纳总结:矩形的四个角都是直角;矩形的对角线相等.
对应训练
1. 矩形具有而一般平行四边形不具有的性质是( )
A. 对边平行
B. 对边相等
C. 对角相等
D. 对角线相等
D
对应训练
2. 如图,在矩形ABCD中,E是AB的中点,连接DE,CE.求证:△ADE≌△BCE.
D
A
B
C
E
∴AD=BC, ∠A=∠B=90°.
证明:∵四边形 ABCD 是矩形,
∵E是AB中点,
∴AE=BE.
∴△ADE≌△BCE(SAS).
对应训练
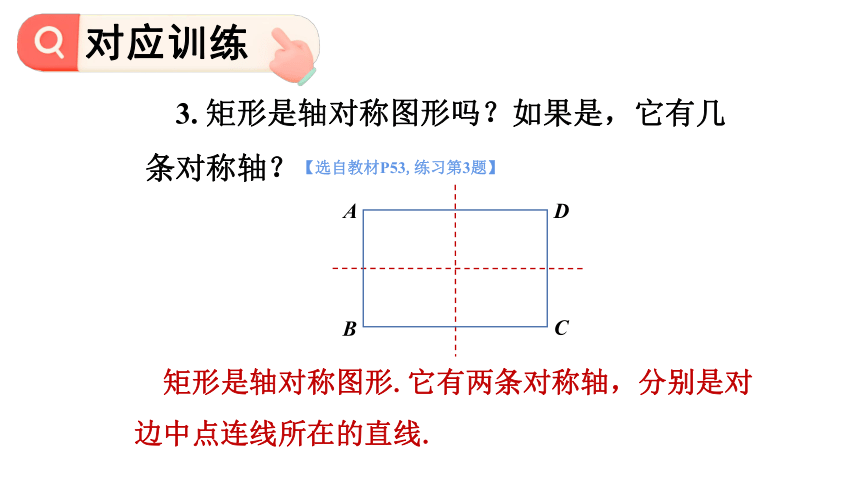
3. 矩形是轴对称图形吗?如果是,它有几条对称轴?
矩形是轴对称图形.它有两条对称轴,分别是对边中点连线所在的直线.
A
B
C
D
【选自教材P53,练习第3题】
直角三角形斜边上的中线性质
新知探究
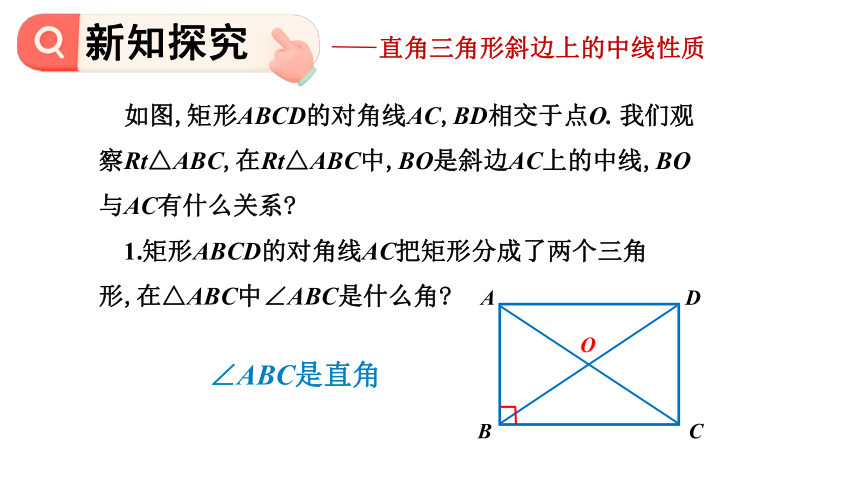
如图,矩形ABCD的对角线AC,BD相交于点O. 我们观察Rt△ABC,在Rt△ABC中,BO是斜边AC上的中线,BO与AC有什么关系
1.矩形ABCD的对角线AC把矩形分成了两个三角
形,在△ABC中∠ABC是什么角
A
B
C
D
O
∠ABC是直角
直角三角形斜边上的中线性质
新知探究
2. AO与CO有什么关系 BO与DO有什么关系
A
B
C
D
AO=CO,BO=DO
3. BO与BD有什么关系 与AC又有什么关系
BO= BD,BO= AC
O
归纳总结:直角三角形斜边上的中线等于斜边的一半.
例1 如图,矩形 ABCD 的对角线 AC ,BD 相交于点 O,∠AOB=60°,AB=4.求矩形对角线的长。
A
B
C
D
O
∵四边形ABCD是矩形,
∴AC与BD相等且互相平分.
∴OA=OB,
又∠AOB=60°
∴△OAB是等边三角形.
∴OA=AB=4 ∴AC=BD=2OA=2×4=8
60°
4
对应训练
1. 如图,在△ABC中,∠ACB=90°,AD=BD , CD=4,则AB的长为( )
A
C
B
D
A
A.8 B. 6 C. 4 D. 2
对应训练
2. 如图,O是矩形ABCD对角线的交点,∠AOD=120°,AE平分∠BAD,则∠EAC= .
15°
A
B
C
D
O
E
120°
对应训练
3. 一个矩形的一条对角线长为8,两条对角线的一个交角为120°.求这个矩形的边长(结果保留小数点后两位).
【选自教材P53,练习第2题】
矩形的性质
利用勾股定理
依题作图
120°
+120°
直角三角形(30°)
A
C
D
O
B
30°
点击查看解题过程
如图所示:
∵四边形ABCD是矩形,
∴AC与BD相等且互相平分,∠ABC=90°.
∴OB=OC.
又∠BOC=120°,
∴∠ACB=30°.
∴AB= AC= 4.
∴BC= .
∴ .
120°
A
C
D
O
B
30°
解:
例2 如图,在矩形ABCD 中,对角线AC,BD 相交于点O,AE⊥BD 于点E,且BE∶ED=1∶3,AD=6cm.求AE 的长.
A
B
D
O
E
∵四边形ABCD是矩形,
∴BO=OD= BD= AC=OA,
∠BAD=90°.
∵BE∶ED=1∶3,∴BE=OE.
又AE⊥BD,∴AB=AO=BO.∴△ABO是等边三角形.
∴∠ABO=60°.∴∠ADE=90°-60°=30°.
∴AE= AD= ×6=3(cm)
C
对应训练
1. 如图,在矩形ABCD 中,对角线AC,BD 相交于点O,点E,F 分别是AO,AD 的中点,连接EF.若AB=6cm,BC=8cm,则EF的长是( ).
A
C
D
O
B
F
E
A. 2.2cm B. 2.3cm
C. 2.4cm D. 2.5cm
D
对应训练
2. 如图,O是矩形ABCD 的对角线AC 的中点, M 是AD 的中点. 若AB=5, AD=12,求四边形ABOM 的周长.
矩形的性质
矩形对角线的长
A
C
D
O
B
M
+勾股定理
直角三角形斜边上的中线的性质
OB的长
三角形的中位线
OM的长
四边形ABOM的周长=AB+OB+OM+AM
点击查看解题过程
∵四边形ABCD是矩形,
∴BC=AD=12,CD=AB=5,∠ABC=90°.
∴AC= .
∵O是AC的中点,∴OB= AC=6.5.
∵M是AD的中点,∴OM是△ACD的中位线.
∴OM= CD=2.5,AM= AD=6.
∴四边形ABOM的周长为:
AB+OB+OM+AM=5+ 6.5+2.5+6=20.
A
C
D
O
B
M
解:
课堂总结
矩形的概念:
矩形的性质:
直角三角形斜边上的中线的性质:
有一个角是直角的平行四边形叫做矩形.
矩形的四个角都是直角;
矩形的对角线相等.
直角三角形斜边上的中线等于斜边的一半.
知识结构
平行
四边形
矩形
性质:边、角、对角线
转化:直角三角形、等腰三角形
课堂练习
1. 在Rt△ABC中,∠C=90°,AB=2AC.求∠A,∠B的度数.
B
C
A
∵△ABC为直角三角形,且AB=2AC
∴∠B=30°
∠A=90°-30°=60°
课堂练习
A
C
B
D
E
2. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD, E是斜边AB的中点.∠ECD是多少度?为什么?
1
2
课堂练习
A
C
B
D
E
1
2
∵△ABC为直角三角形,∠ACB=90°
∴∠A+∠B=90°
又CD⊥AB,∴∠1+∠B=90°.∴∠A=∠1.
∵E是AB的中点,∴CE=AE.
∴∠2=∠A.∴∠1=∠2.
又∠ACD=3∠1,∴∠ECD=∠1+∠2.
∴∠ECD= ∠ACB= ×90°=45°
3. 如图,四边形ABCD是矩形,对角线AC、BD相交于点O,CE∥DB,交AB的延长线于点E.AC和CE相等吗?为什么?
A
C
D
O
B
E
矩形的性质
平行四边形
AC=CE
边相等 (BD=CE)
点击查看解题过程
AE∥DC
对角线相等 (BD=AC)
课堂练习
∵四边形ABCD是矩形,
∴AE∥DC, AC=BD.
又BD∥CE,
∴四边形ABCD为平行四边形.
∴BD=CE.
∴AC=CE.
解:
A
C
D
O
B
E
课堂练习
拓展提升
4. 在矩形ABCD中,AB=5 , AD=12 , 点P是AD、DC上一动点,求点P到两条对角线的距离之和。
A
C
D
O
B
E
F
P
①当点P在AD边上时,
如图所示,作PE⊥AC于点E,PF⊥BD于点F,连接PO.
∵四边形ABCD是矩形,且AB=5,AD=12,
∴AC=BD=13,AO=DO= .
A
C
D
O
B
E
F
P
= AO×(PE+PF)
∴PE+PF=
=15
∴
又
②当点P在DC边上时,
同理可得:
A
C
D
O
B
E
F
P
= OD×(PE+PF)
∴PE+PF=
=15
又
综上所述:点P到两条对角线的距离之和为
第十八章 平行四边形
矩形的性质
情境导入
拿一个活动的平行四边形教具,轻轻拉动一个点,它还是平行四边形吗 使一个角是直角,这时它是什么图形
点击查看平行四边形到矩形的变化过程
平行四边形
一个角是直角
矩形的概念:有一个角是直角的平行四边形叫做矩形,也就是长方形.
仔细观察下列实际生活中的图片,你觉得哪些是矩形的形象
矩形是生活中很常见的图形,你还能列举出矩形在生活中应用的其他例子吗
我们一起来探讨一下矩形的性质吧!
探索新知
探究点1:矩形的性质
如图,取一张矩形纸片,用直尺画出它的对角线.
1.矩形是特殊的平行四边形,它和平行四边形相比,有什么特殊之处?
A
B
C
D
有一个角是直角
探索新知
探究点1:矩形的性质
如图,取一张矩形纸片,用直尺画出它的对角线.
2.平行四边形的对角相等,邻角互补,那么矩形的四个角会有怎样的关系呢?
A
B
C
D
矩形的四个角都相等,都是直角
探索新知
探究点1:矩形的性质
如图,取一张矩形纸片,用直尺画出它的对角线.
3.测量我们刚刚折纸时的两条对角线长度,这两个长度有什么关系?
A
B
C
D
两条对角线长度相等
探索新知
探究点1:矩形的性质
1.如图,在矩形ABCD中,∠A=90°,
求证:∠A=∠B=∠C=∠D=90°.
∴AB∥CD, ∠A=∠C.
证明:∵矩形 ABCD 是特殊的平行四边形,
同理:∠B=90°.∴∠A=∠B=∠C=∠D=90°.
∵∠A=90°,
∴∠C=90°,∠D=180°-90°=90°.
D
A
B
C
下面我们来一起验证一下:
2.如图,四边形ABCD是矩形.求证:AC=BD.
探索新知
探究点1:矩形的性质
A
B
C
D
∴∠ABC=∠DCB=90°.AB=DC.
证明:∵四边形 ABCD 是矩形,
又BC=CB.
在△ABC与△DCB中,
AB=DC
∠ABC=∠DCB
BC=CB
∴△ABC≌△DCB(SAS) ∴AC=BD.
归纳总结:矩形的四个角都是直角;矩形的对角线相等.
对应训练
1. 矩形具有而一般平行四边形不具有的性质是( )
A. 对边平行
B. 对边相等
C. 对角相等
D. 对角线相等
D
对应训练
2. 如图,在矩形ABCD中,E是AB的中点,连接DE,CE.求证:△ADE≌△BCE.
D
A
B
C
E
∴AD=BC, ∠A=∠B=90°.
证明:∵四边形 ABCD 是矩形,
∵E是AB中点,
∴AE=BE.
∴△ADE≌△BCE(SAS).
对应训练
3. 矩形是轴对称图形吗?如果是,它有几条对称轴?
矩形是轴对称图形.它有两条对称轴,分别是对边中点连线所在的直线.
A
B
C
D
【选自教材P53,练习第3题】
直角三角形斜边上的中线性质
新知探究
如图,矩形ABCD的对角线AC,BD相交于点O. 我们观察Rt△ABC,在Rt△ABC中,BO是斜边AC上的中线,BO与AC有什么关系
1.矩形ABCD的对角线AC把矩形分成了两个三角
形,在△ABC中∠ABC是什么角
A
B
C
D
O
∠ABC是直角
直角三角形斜边上的中线性质
新知探究
2. AO与CO有什么关系 BO与DO有什么关系
A
B
C
D
AO=CO,BO=DO
3. BO与BD有什么关系 与AC又有什么关系
BO= BD,BO= AC
O
归纳总结:直角三角形斜边上的中线等于斜边的一半.
例1 如图,矩形 ABCD 的对角线 AC ,BD 相交于点 O,∠AOB=60°,AB=4.求矩形对角线的长。
A
B
C
D
O
∵四边形ABCD是矩形,
∴AC与BD相等且互相平分.
∴OA=OB,
又∠AOB=60°
∴△OAB是等边三角形.
∴OA=AB=4 ∴AC=BD=2OA=2×4=8
60°
4
对应训练
1. 如图,在△ABC中,∠ACB=90°,AD=BD , CD=4,则AB的长为( )
A
C
B
D
A
A.8 B. 6 C. 4 D. 2
对应训练
2. 如图,O是矩形ABCD对角线的交点,∠AOD=120°,AE平分∠BAD,则∠EAC= .
15°
A
B
C
D
O
E
120°
对应训练
3. 一个矩形的一条对角线长为8,两条对角线的一个交角为120°.求这个矩形的边长(结果保留小数点后两位).
【选自教材P53,练习第2题】
矩形的性质
利用勾股定理
依题作图
120°
+120°
直角三角形(30°)
A
C
D
O
B
30°
点击查看解题过程
如图所示:
∵四边形ABCD是矩形,
∴AC与BD相等且互相平分,∠ABC=90°.
∴OB=OC.
又∠BOC=120°,
∴∠ACB=30°.
∴AB= AC= 4.
∴BC= .
∴ .
120°
A
C
D
O
B
30°
解:
例2 如图,在矩形ABCD 中,对角线AC,BD 相交于点O,AE⊥BD 于点E,且BE∶ED=1∶3,AD=6cm.求AE 的长.
A
B
D
O
E
∵四边形ABCD是矩形,
∴BO=OD= BD= AC=OA,
∠BAD=90°.
∵BE∶ED=1∶3,∴BE=OE.
又AE⊥BD,∴AB=AO=BO.∴△ABO是等边三角形.
∴∠ABO=60°.∴∠ADE=90°-60°=30°.
∴AE= AD= ×6=3(cm)
C
对应训练
1. 如图,在矩形ABCD 中,对角线AC,BD 相交于点O,点E,F 分别是AO,AD 的中点,连接EF.若AB=6cm,BC=8cm,则EF的长是( ).
A
C
D
O
B
F
E
A. 2.2cm B. 2.3cm
C. 2.4cm D. 2.5cm
D
对应训练
2. 如图,O是矩形ABCD 的对角线AC 的中点, M 是AD 的中点. 若AB=5, AD=12,求四边形ABOM 的周长.
矩形的性质
矩形对角线的长
A
C
D
O
B
M
+勾股定理
直角三角形斜边上的中线的性质
OB的长
三角形的中位线
OM的长
四边形ABOM的周长=AB+OB+OM+AM
点击查看解题过程
∵四边形ABCD是矩形,
∴BC=AD=12,CD=AB=5,∠ABC=90°.
∴AC= .
∵O是AC的中点,∴OB= AC=6.5.
∵M是AD的中点,∴OM是△ACD的中位线.
∴OM= CD=2.5,AM= AD=6.
∴四边形ABOM的周长为:
AB+OB+OM+AM=5+ 6.5+2.5+6=20.
A
C
D
O
B
M
解:
课堂总结
矩形的概念:
矩形的性质:
直角三角形斜边上的中线的性质:
有一个角是直角的平行四边形叫做矩形.
矩形的四个角都是直角;
矩形的对角线相等.
直角三角形斜边上的中线等于斜边的一半.
知识结构
平行
四边形
矩形
性质:边、角、对角线
转化:直角三角形、等腰三角形
课堂练习
1. 在Rt△ABC中,∠C=90°,AB=2AC.求∠A,∠B的度数.
B
C
A
∵△ABC为直角三角形,且AB=2AC
∴∠B=30°
∠A=90°-30°=60°
课堂练习
A
C
B
D
E
2. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD, E是斜边AB的中点.∠ECD是多少度?为什么?
1
2
课堂练习
A
C
B
D
E
1
2
∵△ABC为直角三角形,∠ACB=90°
∴∠A+∠B=90°
又CD⊥AB,∴∠1+∠B=90°.∴∠A=∠1.
∵E是AB的中点,∴CE=AE.
∴∠2=∠A.∴∠1=∠2.
又∠ACD=3∠1,∴∠ECD=∠1+∠2.
∴∠ECD= ∠ACB= ×90°=45°
3. 如图,四边形ABCD是矩形,对角线AC、BD相交于点O,CE∥DB,交AB的延长线于点E.AC和CE相等吗?为什么?
A
C
D
O
B
E
矩形的性质
平行四边形
AC=CE
边相等 (BD=CE)
点击查看解题过程
AE∥DC
对角线相等 (BD=AC)
课堂练习
∵四边形ABCD是矩形,
∴AE∥DC, AC=BD.
又BD∥CE,
∴四边形ABCD为平行四边形.
∴BD=CE.
∴AC=CE.
解:
A
C
D
O
B
E
课堂练习
拓展提升
4. 在矩形ABCD中,AB=5 , AD=12 , 点P是AD、DC上一动点,求点P到两条对角线的距离之和。
A
C
D
O
B
E
F
P
①当点P在AD边上时,
如图所示,作PE⊥AC于点E,PF⊥BD于点F,连接PO.
∵四边形ABCD是矩形,且AB=5,AD=12,
∴AC=BD=13,AO=DO= .
A
C
D
O
B
E
F
P
= AO×(PE+PF)
∴PE+PF=
=15
∴
又
②当点P在DC边上时,
同理可得:
A
C
D
O
B
E
F
P
= OD×(PE+PF)
∴PE+PF=
=15
又
综上所述:点P到两条对角线的距离之和为
