苏教版九年级上册期末过关练习(含答案)
图片预览

文档简介
中小学教育资源及组卷应用平台
期末过关练习-数学九年级上册苏教版
一、选择题
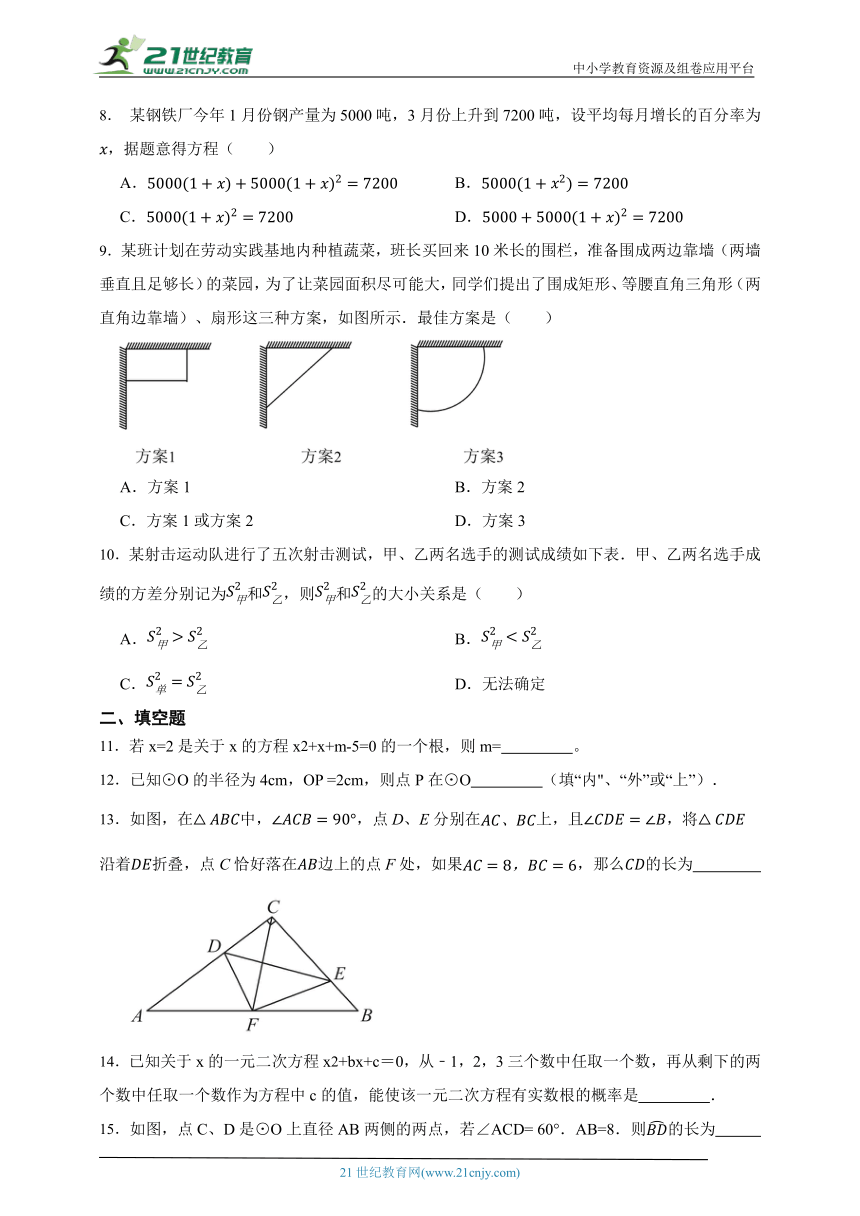
1.已知圆锥的底面半径为4cm,母线长为5cm,则这个圆锥的侧面积是( )
A.20πcm2 B.20cm2 C.40πcm2 D.40cm2
2.一元二次方程x2+4x=﹣3用配方法变形正确的是( )
A.(x﹣2) =1 B.(x+2) =1
C.(x﹣2) =﹣1 D.(x+2) =﹣1
3.如图,在Rt△ABC中,∠ACB=90°,AC=3,以点C为圆心,CA为半径的圆与AB交于点D,若点D恰好为线段AB的中点,则AB的长度为( )
A. B.3 C.9 D.6
4.下列方程两根之和是-2的是( )
A.x2-2x-3=0 B.x2+2x-3=0 C.x2+2x+3=0 D.x2-2x+3=0
5.下列事件中,属于必然事件的是( )
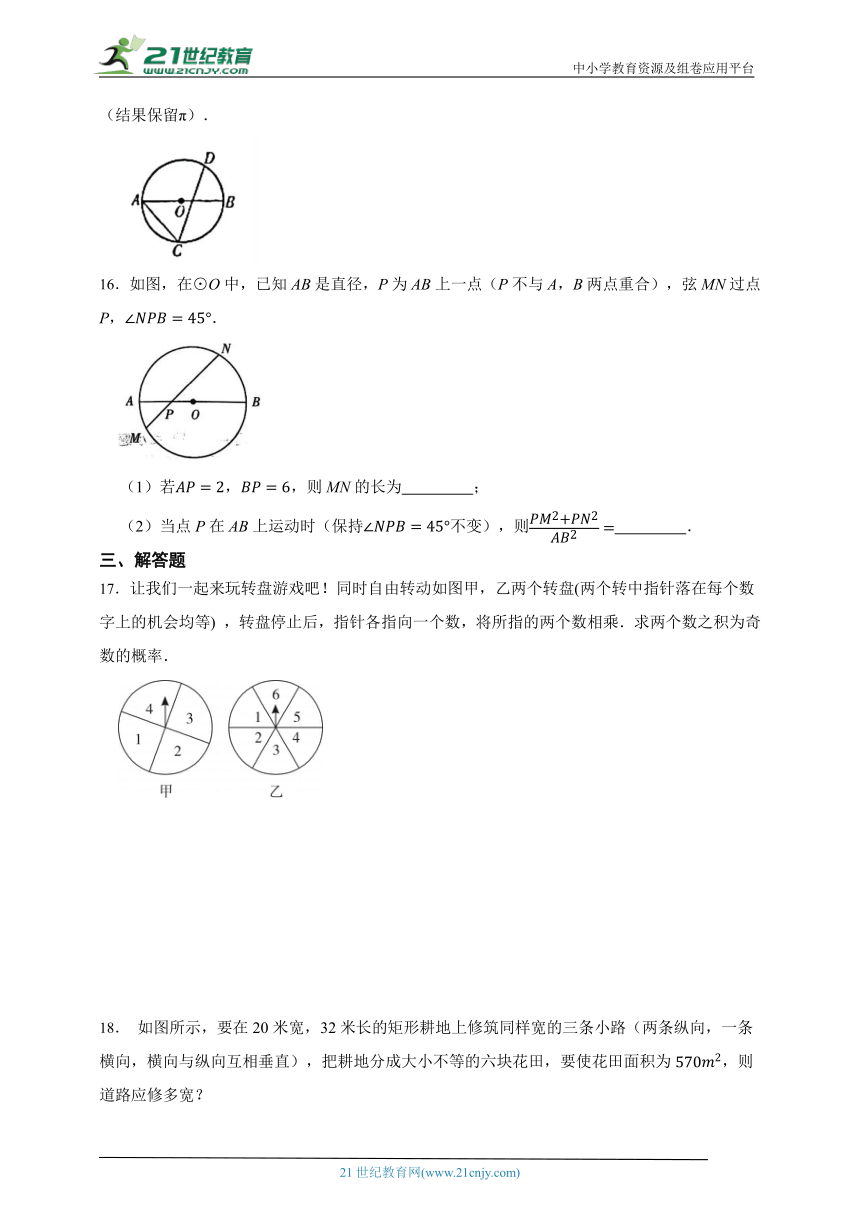
A.抛掷硬币时,正面朝上 B.小明发烧了,体温达到50℃
C.经过红绿灯路口,遇到红灯 D.任意写一个负数,小于正数
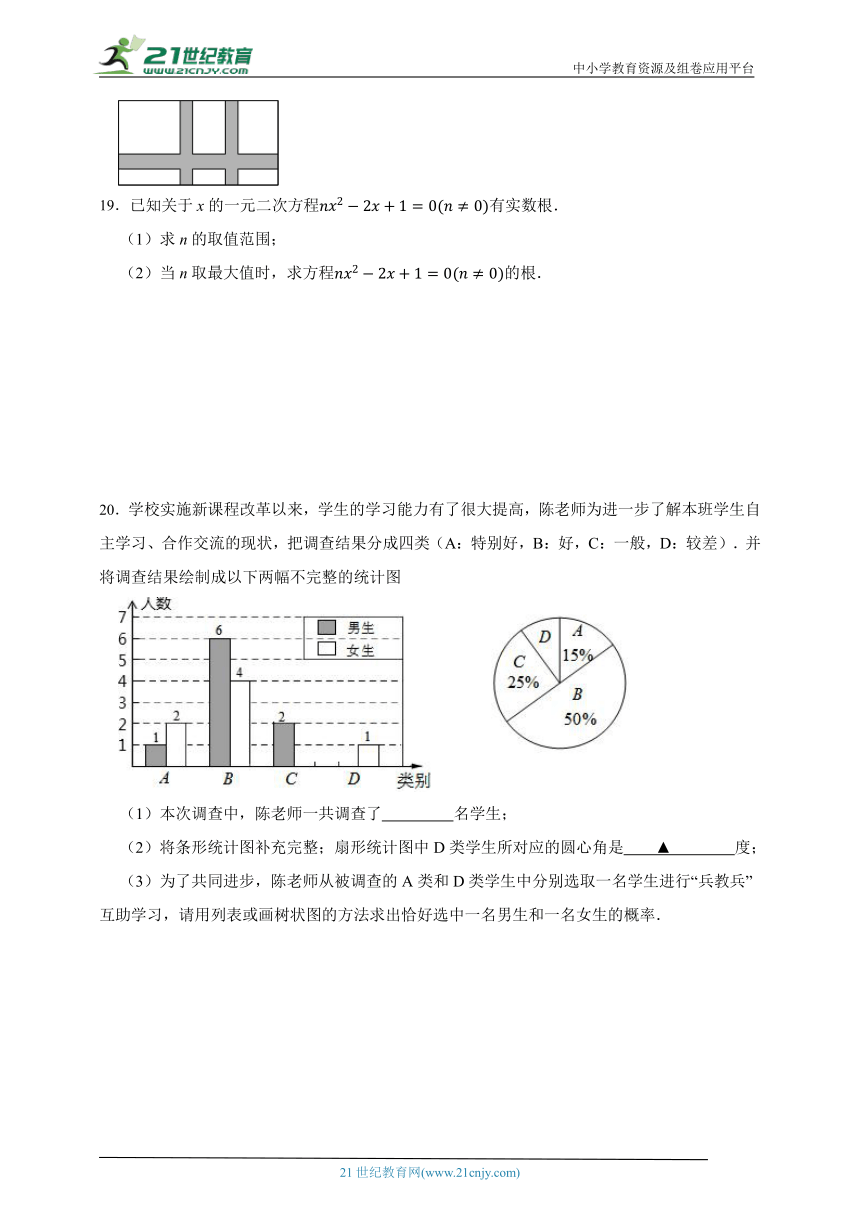
6.为了解某地区九年级男生的身高情况,随机抽取了该地区100名九年级男生,他们的身高x(cm)统计如下:
组别(cm) x<160 160≤x<170 170≤x<180 x≥180
人数 5 38 42 15
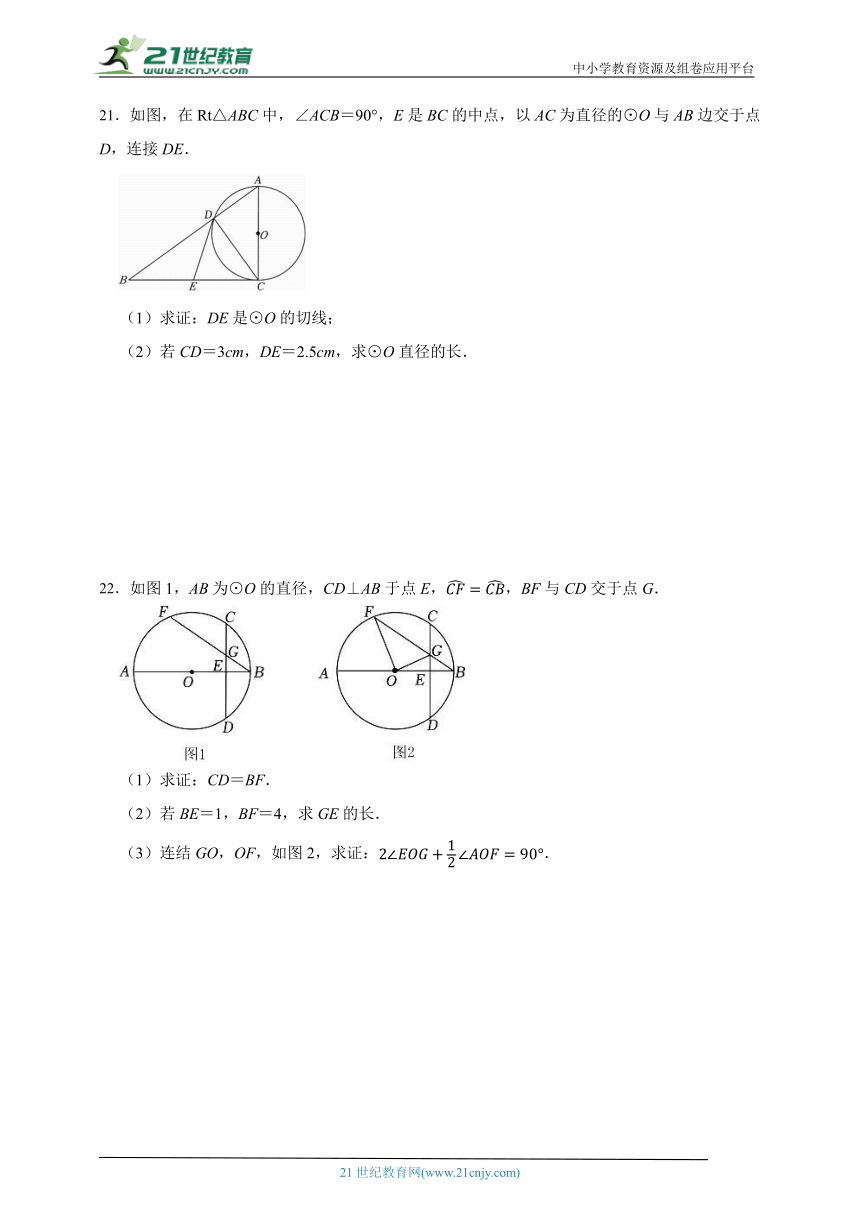
根据以上结果,任意抽查该地区一名九年级男生,他的身高不小于180 cm的概率是( )
A.0.85. B.0.57. C.0.42. D.0.15.
7.向阳村前年的人均年收入为16000元,今年的人均年收入为24520元.设人均年收入的平均增长率为x,则下列所列的方程中正确的是( )
A. B.
C. D.
8. 某钢铁厂今年1月份钢产量为5000吨,3月份上升到7200吨,设平均每月增长的百分率为,据题意得方程( )
A. B.
C. D.
9.某班计划在劳动实践基地内种植蔬菜,班长买回来10米长的围栏,准备围成两边靠墙(两墙垂直且足够长)的菜园,为了让菜园面积尽可能大,同学们提出了围成矩形、等腰直角三角形(两直角边靠墙)、扇形这三种方案,如图所示.最佳方案是( )
A.方案1 B.方案2
C.方案1或方案2 D.方案3
10.某射击运动队进行了五次射击测试,甲、乙两名选手的测试成绩如下表.甲、乙两名选手成绩的方差分别记为和,则和的大小关系是( )
A. B.
C. D.无法确定
二、填空题
11.若x=2是关于x的方程x2+x+m-5=0的一个根,则m= 。
12.已知⊙O的半径为4cm,OP =2cm,则点P在⊙O (填“内"、“外”或“上”).
13.如图,在中,,点D、E分别在上,且,将沿着折叠,点C恰好落在边上的点F处,如果,那么的长为
14.已知关于x的一元二次方程x2+bx+c=0,从﹣1,2,3三个数中任取一个数,再从剩下的两个数中任取一个数作为方程中c的值,能使该一元二次方程有实数根的概率是 .
15.如图,点C、D是⊙O上直径AB两侧的两点,若∠ACD= 60°.AB=8.则的长为 (结果保留π).
16.如图,在⊙O中,已知AB是直径,P为AB上一点(P不与A,B两点重合),弦MN过点P,.
(1)若,,则MN的长为 ;
(2)当点P在AB上运动时(保持不变),则 .
三、解答题
17.让我们一起来玩转盘游戏吧!同时自由转动如图甲,乙两个转盘(两个转中指针落在每个数字上的机会均等) ,转盘停止后,指针各指向一个数,将所指的两个数相乘.求两个数之积为奇数的概率.
18. 如图所示,要在20米宽,32米长的矩形耕地上修筑同样宽的三条小路(两条纵向,一条横向,横向与纵向互相垂直),把耕地分成大小不等的六块花田,要使花田面积为,则道路应修多宽?
19.已知关于x的一元二次方程有实数根.
(1)求n的取值范围;
(2)当n取最大值时,求方程的根.
20.学校实施新课程改革以来,学生的学习能力有了很大提高,陈老师为进一步了解本班学生自主学习、合作交流的现状,把调查结果分成四类(A:特别好,B:好,C:一般,D:较差).并将调查结果绘制成以下两幅不完整的统计图
(1)本次调查中,陈老师一共调查了 名学生;
(2)将条形统计图补充完整;扇形统计图中D类学生所对应的圆心角是 ▲ 度;
(3)为了共同进步,陈老师从被调查的A类和D类学生中分别选取一名学生进行“兵教兵”互助学习,请用列表或画树状图的方法求出恰好选中一名男生和一名女生的概率.
21.如图,在Rt△ABC中,∠ACB=90°,E是BC的中点,以AC为直径的⊙O与AB边交于点D,连接DE.
(1)求证:DE是⊙O的切线;
(2)若CD=3cm,DE=2.5cm,求⊙O直径的长.
22.如图1,AB为⊙O的直径,CD⊥AB于点E,,BF与CD交于点G.
(1)求证:CD=BF.
(2)若BE=1,BF=4,求GE的长.
(3)连结GO,OF,如图2,求证:.
答案解析部分
1.【答案】A
2.【答案】B
3.【答案】D
4.【答案】B
5.【答案】D
6.【答案】D
7.【答案】B
8.【答案】C
9.【答案】D
10.【答案】A
11.【答案】-1
12.【答案】内
13.【答案】
14.【答案】
15.【答案】
16.【答案】(1)
(2)
17.【答案】解:根据题意画出树状图如下:
由图可知:共有24种等可能的结果数,其中两数之积为奇数的情况数有6种,
∴P( 两个数之积为奇数)=.
18.【答案】解:设道路应修宽,根据题意得:
,
整理得:,
解得:(不合题意,舍去),
答:道路应修宽.
19.【答案】(1)解:,
由“关于x的一元二次方程有实数根”得:
,即:,
解得:.
又∵,
∴n的取值范围是且.
(2)解:由且得:n的最大值为1,
把代入原方程得:
化简得:,
∴,
解得:.
20.【答案】(1)20
(2)解:如图
;36
(3)解:列表如下,A类学生中的两名女生分别记为A1和A2,
女A6 女A2 男A
男D 女A1男D 女A3男D 男A男D
女D 女A1女D 女A2女D 男A女D
共有3种等可能的结果,其中,所以所选两位同学恰好是一位男生和一位女生的概率为=.
21.【答案】(1)解:∵AC是⊙O的直径,
∴∠ADC=∠BDC=90°,
∵E是BC的中点,
∴ED=EC,
∴∠EDC=∠ECD,
∵OD=OC,
∴∠ODC=∠OCD,
∵∠ACB=90°,
∴∠OCD+∠ECD=90°,
∴∠EDC+∠ODC=90°,
∵OD为半径,
∴DE是⊙O的切线
(2)解:∵DE是Rt△BDC斜边上的中线,DE=25cm,CD=3cm,
∴BC=2DE=5cm,
∴BD===4(cm),
设AD=X,∵CD2+AD2=AB2-BC2
∴9+x2=(4+x)2-25解得x=9/4
∴AC=15/4
22.【答案】(1)证明:∵AB为⊙O的直径,CD⊥AB于点E,
∴,
∵,
∴,
∴,即,
∴BF=CD;
(2)解:如图所示:连接BC,
由(1)得:,CD=BF=4,
∴∠FBC=∠BCD,
∴BG=CG,
∵AB为⊙O的直径,CD⊥AB于点E,
∴,
设EG=x,则BG=CG=2﹣x,
在△BEG中,EG2+BE2=BG2,即x2+12=(2﹣x)2,
解得:,
∴GE的长为;
(3)解:如图所示:连接OC交BF于I,
∵,
∴,
在△OCG和△OBG中,
,
∴△OCG≌△OBG(SSS),
∴∠COG=∠BOG,
∴∠IOB=2∠EOG,
∵OF=OB,OC为半径,
∴OC⊥BF,
∴∠OIB=90°,
∵∠IOB+∠IBO=90°,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末过关练习-数学九年级上册苏教版
一、选择题
1.已知圆锥的底面半径为4cm,母线长为5cm,则这个圆锥的侧面积是( )
A.20πcm2 B.20cm2 C.40πcm2 D.40cm2
2.一元二次方程x2+4x=﹣3用配方法变形正确的是( )
A.(x﹣2) =1 B.(x+2) =1
C.(x﹣2) =﹣1 D.(x+2) =﹣1
3.如图,在Rt△ABC中,∠ACB=90°,AC=3,以点C为圆心,CA为半径的圆与AB交于点D,若点D恰好为线段AB的中点,则AB的长度为( )
A. B.3 C.9 D.6
4.下列方程两根之和是-2的是( )
A.x2-2x-3=0 B.x2+2x-3=0 C.x2+2x+3=0 D.x2-2x+3=0
5.下列事件中,属于必然事件的是( )
A.抛掷硬币时,正面朝上 B.小明发烧了,体温达到50℃
C.经过红绿灯路口,遇到红灯 D.任意写一个负数,小于正数
6.为了解某地区九年级男生的身高情况,随机抽取了该地区100名九年级男生,他们的身高x(cm)统计如下:
组别(cm) x<160 160≤x<170 170≤x<180 x≥180
人数 5 38 42 15
根据以上结果,任意抽查该地区一名九年级男生,他的身高不小于180 cm的概率是( )
A.0.85. B.0.57. C.0.42. D.0.15.
7.向阳村前年的人均年收入为16000元,今年的人均年收入为24520元.设人均年收入的平均增长率为x,则下列所列的方程中正确的是( )
A. B.
C. D.
8. 某钢铁厂今年1月份钢产量为5000吨,3月份上升到7200吨,设平均每月增长的百分率为,据题意得方程( )
A. B.
C. D.
9.某班计划在劳动实践基地内种植蔬菜,班长买回来10米长的围栏,准备围成两边靠墙(两墙垂直且足够长)的菜园,为了让菜园面积尽可能大,同学们提出了围成矩形、等腰直角三角形(两直角边靠墙)、扇形这三种方案,如图所示.最佳方案是( )
A.方案1 B.方案2
C.方案1或方案2 D.方案3
10.某射击运动队进行了五次射击测试,甲、乙两名选手的测试成绩如下表.甲、乙两名选手成绩的方差分别记为和,则和的大小关系是( )
A. B.
C. D.无法确定
二、填空题
11.若x=2是关于x的方程x2+x+m-5=0的一个根,则m= 。
12.已知⊙O的半径为4cm,OP =2cm,则点P在⊙O (填“内"、“外”或“上”).
13.如图,在中,,点D、E分别在上,且,将沿着折叠,点C恰好落在边上的点F处,如果,那么的长为
14.已知关于x的一元二次方程x2+bx+c=0,从﹣1,2,3三个数中任取一个数,再从剩下的两个数中任取一个数作为方程中c的值,能使该一元二次方程有实数根的概率是 .
15.如图,点C、D是⊙O上直径AB两侧的两点,若∠ACD= 60°.AB=8.则的长为 (结果保留π).
16.如图,在⊙O中,已知AB是直径,P为AB上一点(P不与A,B两点重合),弦MN过点P,.
(1)若,,则MN的长为 ;
(2)当点P在AB上运动时(保持不变),则 .
三、解答题
17.让我们一起来玩转盘游戏吧!同时自由转动如图甲,乙两个转盘(两个转中指针落在每个数字上的机会均等) ,转盘停止后,指针各指向一个数,将所指的两个数相乘.求两个数之积为奇数的概率.
18. 如图所示,要在20米宽,32米长的矩形耕地上修筑同样宽的三条小路(两条纵向,一条横向,横向与纵向互相垂直),把耕地分成大小不等的六块花田,要使花田面积为,则道路应修多宽?
19.已知关于x的一元二次方程有实数根.
(1)求n的取值范围;
(2)当n取最大值时,求方程的根.
20.学校实施新课程改革以来,学生的学习能力有了很大提高,陈老师为进一步了解本班学生自主学习、合作交流的现状,把调查结果分成四类(A:特别好,B:好,C:一般,D:较差).并将调查结果绘制成以下两幅不完整的统计图
(1)本次调查中,陈老师一共调查了 名学生;
(2)将条形统计图补充完整;扇形统计图中D类学生所对应的圆心角是 ▲ 度;
(3)为了共同进步,陈老师从被调查的A类和D类学生中分别选取一名学生进行“兵教兵”互助学习,请用列表或画树状图的方法求出恰好选中一名男生和一名女生的概率.
21.如图,在Rt△ABC中,∠ACB=90°,E是BC的中点,以AC为直径的⊙O与AB边交于点D,连接DE.
(1)求证:DE是⊙O的切线;
(2)若CD=3cm,DE=2.5cm,求⊙O直径的长.
22.如图1,AB为⊙O的直径,CD⊥AB于点E,,BF与CD交于点G.
(1)求证:CD=BF.
(2)若BE=1,BF=4,求GE的长.
(3)连结GO,OF,如图2,求证:.
答案解析部分
1.【答案】A
2.【答案】B
3.【答案】D
4.【答案】B
5.【答案】D
6.【答案】D
7.【答案】B
8.【答案】C
9.【答案】D
10.【答案】A
11.【答案】-1
12.【答案】内
13.【答案】
14.【答案】
15.【答案】
16.【答案】(1)
(2)
17.【答案】解:根据题意画出树状图如下:
由图可知:共有24种等可能的结果数,其中两数之积为奇数的情况数有6种,
∴P( 两个数之积为奇数)=.
18.【答案】解:设道路应修宽,根据题意得:
,
整理得:,
解得:(不合题意,舍去),
答:道路应修宽.
19.【答案】(1)解:,
由“关于x的一元二次方程有实数根”得:
,即:,
解得:.
又∵,
∴n的取值范围是且.
(2)解:由且得:n的最大值为1,
把代入原方程得:
化简得:,
∴,
解得:.
20.【答案】(1)20
(2)解:如图
;36
(3)解:列表如下,A类学生中的两名女生分别记为A1和A2,
女A6 女A2 男A
男D 女A1男D 女A3男D 男A男D
女D 女A1女D 女A2女D 男A女D
共有3种等可能的结果,其中,所以所选两位同学恰好是一位男生和一位女生的概率为=.
21.【答案】(1)解:∵AC是⊙O的直径,
∴∠ADC=∠BDC=90°,
∵E是BC的中点,
∴ED=EC,
∴∠EDC=∠ECD,
∵OD=OC,
∴∠ODC=∠OCD,
∵∠ACB=90°,
∴∠OCD+∠ECD=90°,
∴∠EDC+∠ODC=90°,
∵OD为半径,
∴DE是⊙O的切线
(2)解:∵DE是Rt△BDC斜边上的中线,DE=25cm,CD=3cm,
∴BC=2DE=5cm,
∴BD===4(cm),
设AD=X,∵CD2+AD2=AB2-BC2
∴9+x2=(4+x)2-25解得x=9/4
∴AC=15/4
22.【答案】(1)证明:∵AB为⊙O的直径,CD⊥AB于点E,
∴,
∵,
∴,
∴,即,
∴BF=CD;
(2)解:如图所示:连接BC,
由(1)得:,CD=BF=4,
∴∠FBC=∠BCD,
∴BG=CG,
∵AB为⊙O的直径,CD⊥AB于点E,
∴,
设EG=x,则BG=CG=2﹣x,
在△BEG中,EG2+BE2=BG2,即x2+12=(2﹣x)2,
解得:,
∴GE的长为;
(3)解:如图所示:连接OC交BF于I,
∵,
∴,
在△OCG和△OBG中,
,
∴△OCG≌△OBG(SSS),
∴∠COG=∠BOG,
∴∠IOB=2∠EOG,
∵OF=OB,OC为半径,
∴OC⊥BF,
∴∠OIB=90°,
∵∠IOB+∠IBO=90°,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
