第六单元 平移、旋转和轴对称复习课件(共26张PPT)2023-2024学年三年级数学上册期末核心考点集训(苏教版)
文档属性
| 名称 | 第六单元 平移、旋转和轴对称复习课件(共26张PPT)2023-2024学年三年级数学上册期末核心考点集训(苏教版) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-21 19:23:34 | ||
图片预览






文档简介
(共26张PPT)
第六单元
平移、旋转和轴对称
期末考点集训
2023-2024学年苏教版数学三年级上册
知识解读
知识点01:平移和旋转
1.平移:物体或图形沿着直线做运动
2.旋转:一个物体或图形绕着一个点或一个轴转动的现象。
3.平移和旋转都是物体或图形运动的现象,运动中物体的形状和大小都不变;二者的区别在于:平移是物体做直线运动,而旋转是物体绕一个点或轴转动,平移只改变位置,旋转改变的是方向和位置。
知识点02:轴对称图形
1.轴对称图形:把一个图形沿着某一条直线对折,对折后折痕两侧的部分能完全重合,这样的图形就是轴对称图形。折痕所在的直线是图形的对称轴。
2.轴对称图形的特征:对折后,对称轴两侧能完全重合。
易错点01:平移和旋转
1. 判断平移现象时,要看物体是不是沿直线运动。
2. 物体绕着某一个点运动就是旋转,不一定要转动一周。
易错点02:轴对称图形
1.轴对称图形沿对称轴对折后,两边能够完全重合。
易错点拨
考点目录
【考点01】轴对称的概念
【考点02】确定轴对称图形的对称轴条数及位置
【考点03】作轴对称图形
【考点04】画轴对称图形的对称轴
【考点05】画轴对称图形的对称轴
【考点06】镜面对称
【考点07】平移的概念
【考点08】作平移后的图形
【考点09】旋转的概念
【考点10】作旋转一定角度后的图形
【考点11】运用平移、对称和旋转设计图案
考点精讲练
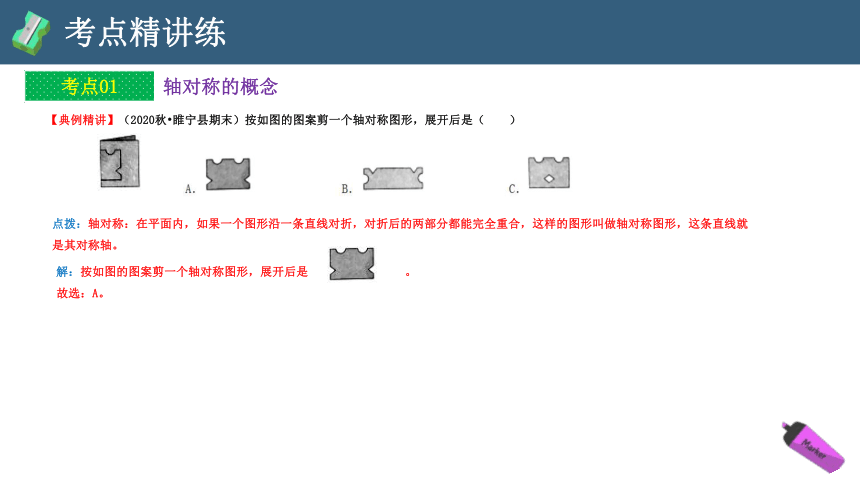
【典例精讲】(2020秋 睢宁县期末)按如图的图案剪一个轴对称图形,展开后是( )
考点01 轴对称的概念
点拨:轴对称:在平面内,如果一个图形沿一条直线对折,对折后的两部分都能完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴。
解:按如图的图案剪一个轴对称图形,展开后是 。
故选:A。
考点精讲练
【真题强化】(2020秋 东海县校级月考)下面的图案各是从哪张纸上剪下来的?连一连。
考点01 轴对称的概念
点拨:依据轴对称图形的概念,即在平面内,如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴,据此解答即可。
解:
考点精讲练
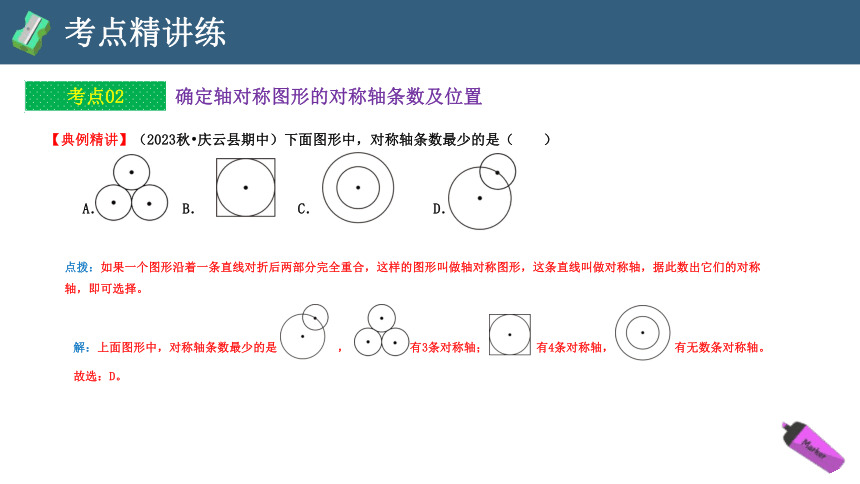
【典例精讲】(2023秋 庆云县期中)下面图形中,对称轴条数最少的是( )
A. B. C. D.
考点02 确定轴对称图形的对称轴条数及位置
点拨:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴,据此数出它们的对称轴,即可选择。
解:上面图形中,对称轴条数最少的是 , 有3条对称轴; 有4条对称轴, 有无数条对称轴。
故选:D。
考点精讲练
【真题强化】(2023秋 岷县期中)如图所示是轴对称图形的有( )个.
A.1 B.2 C.3 D.4
考点02 确定轴对称图形的对称轴条数及位置
点拨:根据轴对称图形的概念:一个图形沿某条直线对折,直线两旁的部分能够完全重合,这个图形就是轴对称图形,由此对各图形分析判断后即可求解.
解:图1是轴对称图形,图2不是轴对称图形;图3是轴对称图形;图4是轴对称图形;图5不轴对称图形,
所以一共有3个图形是轴对称图形.
故选:C.
考点精讲练
【典例精讲】(2023春 离石区期末)如图是一些国家的国旗,其中是轴对称图形的有( )
A.4个 B.3个 C.2个 D.1个
考点03 轴对称图形的辨识
点拨:根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;依次进行判断即可.
解:根据轴对称图形的意义可知:加拿大、摩洛哥、瑞典的国旗都是轴对称图形,而澳大利亚的国旗不是轴对称图形;
故选:B.
考点精讲练
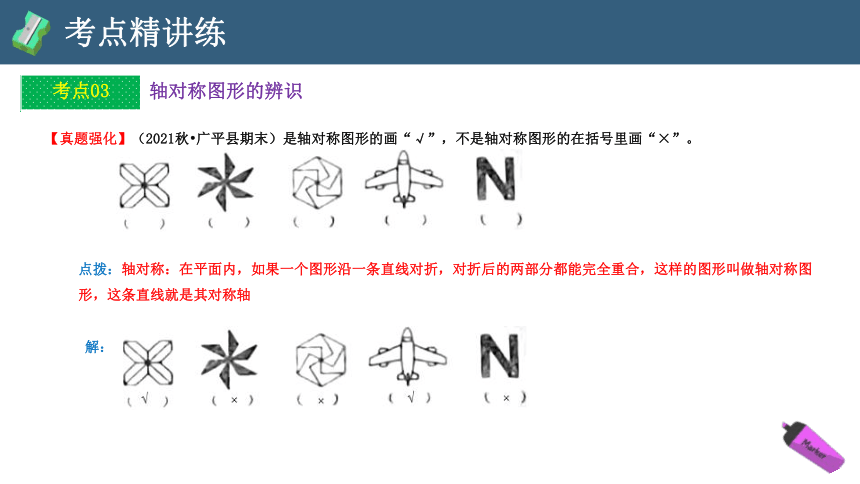
【真题强化】(2021秋 广平县期末)是轴对称图形的画“√”,不是轴对称图形的在括号里画“×”。
考点03 轴对称图形的辨识
点拨:轴对称:在平面内,如果一个图形沿一条直线对折,对折后的两部分都能完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴
解:
考点精讲练
【典例精讲】(2021秋 如东县期末)如图是用边长1厘米的小正方形拼成。图中涂色部分占整个图形的 ,涂色部分的周长是 厘米。想象一下,把涂色部分去掉一格,使得剩下的涂色部分变成一个轴对称图形,有 种不同的方法。
考点04 作轴对称图形
点拨:把整个长方形的面积看作一个整体,把它平均分成8份,每份是它的 ,其中5份涂色,表示 ;求涂色部分的周长,可能数格的方法数出;把涂色部分去掉一格,使得剩下的涂色部分变成一个轴对称图形,可去掉第一行的或去掉下行右边一个,即有2种不同的方法。
解:用边长1厘米的小正方形拼成。图中涂色部分占整个图形的 ,涂色部分的周长是12厘米。想象一下,把涂色部分去掉一格,使得剩下的涂色部分变成一个轴对称图形,有2种不同的方法。
故答案为:,12,2。
考点精讲练
【真题强化】(2023秋 宿州月考)按要求做。
(1)画出图①中图形的对称轴。
(2)在图②已知图形的基础上再涂2格,使涂色部分成为轴对称图形。
考点04 作轴对称图形
点拨:(1)根据轴对称图形的特征,如果一个图形沿着一条直线打折,左右完全重合,这个图形就是轴对称图形,这条直线就是对称轴。据此作图即可。
(2)根据轴对称图形的特征,如果一个图形沿着一条直线打折,左右完全重合,这个图形就是轴对称图形,这条直线就是对称轴。据此作图即可。(答案不唯一)
解:(1)画出图①中图形的对称轴。作图如下:
(2)在图②已知图形的基础上再涂2格,使涂色部分成为轴对称图形。作图如下:
(答案不唯一)
考点精讲练
【典例精讲】(2023秋 榕城区期中)在如图中,再选3格涂色,使它们构成一幅轴对称图形,并画出它的对称轴。
考点05 画轴对称图形的对称轴
点拨:如果一个图形沿着一条直线折叠后,直线两旁的部分能够完全重合,那么这个图形就叫作轴对称图形,折痕所在的直线就是对称轴,再选择3格涂上颜色,使它们构成一幅轴对称图形即可。
解:作图如下:
(画法不唯一,合理即可)
考点精讲练
【真题强化】(2021秋 威县期末)描一描,画一画。
(1)用彩笔描出下面图形的周长。
(2)在下面轴对称图形中画出一条对称轴。
考点05 画轴对称图形的对称轴
点拨:(1)根据周长的含义:物体的边缘或围成平面图形一周的长,叫做它的周长;由此用彩笔沿图形的一周描出图形的周长即可;
(2)根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;据此判断,然后画出一条对称轴即可。
解:(1) (2)
考点精讲练
【典例精讲】(2021秋 福鼎市期末)小明看到河边的岸上有一座房子的形状如图,那么他看到房子在水中的倒影应该是( )
A. B.
C. D.
考点06 镜面对称
点拨:根据镜面对称的特征,镜中的景物与实际景物上下前后方向一致,左右方向相反,大小不变,且关于镜面对称。
解:根据分析可知,房子和它的倒影是以水面为对称轴的轴对称图形。
故选:D。
考点精讲练
【真题强化】(2019秋 观山湖区期末)如图是从镜中看到的一串数字,这串数字应为 .
考点06 镜面对称
点拨:根据镜面对称的性质求解,在平面镜中的像与现实中的事物恰好左右顺序颠倒,且关于镜面对称.
解:如图 是从镜中看到的一串数字,这串数字应为810076;
故答案为:810076.
考点精讲练
【典例精讲】(2023秋 礼泉县期中)如图,图形甲( )才能将最下面一行填满。
A.先向右平移2格,再向下平移2格
B.先向右平移3格,再向下平移2格
C.先向右平移3格,再向下平移3格
D.先向右平移2格,再向下平移3格
考点07 平移的概念
点拨:平移是物体运动时,物体上任意两点间,从一点到另一点的方向与距离都不变的运动,平移后图形的位置改变,形状、大小不变;据此解答即可。
解:如图,图形甲先向右平移3格,再向下平移3格才能将最下面一行填满。
故选:C。
考点精讲练
【真题强化】(2023春 吉利区期末)如图,由图A到图B是向 平移了 格,由图B到图C是向 平移了 格.
考点07 平移的概念
点拨:根据图中两图的相对距离及箭头指向即可确定平移的方向和距离,所以图A到图B是向 右平移了 6格,由图B到图C是向 下平移了 2格;由此解答即可.
解:如图,由图A到图B是向 右平移了 6格,由图B到图C是向 下平移了 2格.
故答案为:右,6,下,2.
考点精讲练
【典例精讲】(2023秋 礼泉县期中)(1)以虚线为对称轴,点P的对称点是点 。
(2)图形甲先向下平移 格,再向右平移 格可以得到图形乙。
考点08 作平移后的图形
点拨:(1)根据对称的意义,即可解答;(2)找准方向,数清格数,即可解答。
解:(1)以虚线为对称轴,点P的对称点是点B。
(2)图形甲先向下平移3格,再向右平移5格可以得到图形乙。
故答案为:B;3,5。
考点精讲练
【真题强化】(2023秋 滕州市期中)图一中左侧的图形先向 平移 格,再向 平移 格就得到右侧的图形。图二中左侧的图形先向 平移 格,再向 平移 格就得到右侧的图形。
考点08 作平移后的图形
点拨:确定平移后图形的基本要素有两个:平移方向、平移距离,结合题意分析分析解答即可。
解:图一中左侧的图形先向下平移2格,再向右平移3格就得到右侧的图形。图二中左侧的图形先向上平移3格,再向右平移3格就得到右侧的图形。
故答案为:下,2,右,3,上,3,右,3。
考点精讲练
【典例精讲】(2023秋 项城市期中)如图,从12:00到3:00,时针沿顺时针方向旋转了( )°。
A.90 B.60 C.180
考点09 旋转的概念
点拨:钟面上12个数字,以表芯为旋转点,表针转一圈是360°,被12个数字平均分成12份,每一份也就是两数之间夹角是30°;从12:00到3:00,时针沿顺时针方向旋转了3大格,是3×30°=90°。据此解答即可。
解:3×30°=90°
答:从12:00到3:00,时针沿顺时针方向旋转了90°。
故选:A。
考点精讲练
【真题强化】(2023秋 沈丘县期中)(1)图形①绕点O沿逆时针方向旋转 ,得到图形④。
(2)图形②绕点O沿 时针方向旋转90°,得到图形③。
(3)图形①可以看作是图形 沿逆时针方向旋转90°得到的,还可以看作是图形 沿顺时针方向旋转90°得到的。
考点09 旋转的概念
点拨:根据旋转知识,先确定旋转的中心,再观察是按顺时针方向旋转,还是按逆时针方向旋转,最后确定旋转的度数即可。
解:(1)图形①绕点O沿逆时针方向旋转90°,得到图形④。
(2)图形②绕点O沿顺时针方向旋转90°,得到图形③。
(3)图形①可以看作是图形②沿逆时针方向旋转90°得到的,还可以看作是图形④沿顺时针方向旋转90°得到的。
故答案为:90;顺;②,④。
考点精讲练
【典例精讲】(2023 朝阳区模拟)图形A经过( )运动后可变成图形B。
A.绕Q点逆时针旋转90°,再向下平移2格
B.绕Q点顺时针旋转90°,再向下平移2格
C.绕P点逆时针旋转90°,再向右平移2格
考点10 作旋转一定角度后的图形
点拨:根据图形的旋转和平移知识,图形A经过绕Q点顺时针旋转90°,再向下平移2格运动后可变成图形B,据此解答即可。
解:图形A经过绕Q点顺时针旋转90°,再向下平移2格运动后可变成图形B。
故选:B。
考点精讲练
【真题强化】(2023秋 庆云县期中)按要求画一画。
①画出梯形绕A点顺时针旋转90°后的图形。
②把平行四边形向右平移6格,画出平移后的图形。
③把如图所示图形补全,使它成为一个轴对称图形。
考点10 作旋转一定角度后的图形
点拨:①根据旋转的特征,梯形绕点A顺时针旋转90°,点A的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形;
②根据平移的特征,把平行四边形的各顶点分别向向右平移6格,依次连接即可得到平移后的图形;
③根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴(虚线)的下边画上半左图的关键对称点,依次连接即可。
解:根据题意画图如下:
考点精讲练
【典例精讲】(2019秋 玉门市期末)请按照给出的对称轴画出第一个图形的对称图形,第二个图形请向上移动3格.
考点11 运用平移、对称和旋转设计图案
点拨:按照给出的对称轴画出第一个图形的对称图形:找出5个关键点(图形中的顶点)关于对称轴的对称点,连接这5个对称点,填充黑色,即可得解.
第二个图形向上移动3格,找出5个关键点(图形中的顶点)向上移动3格,连接这5个端点,填充黑色,即可得解.
解:作图如上:
考点精讲练
【真题强化】(1)小明家的客厅地面是一个正方形,如图1.要用图2所示的长方形地砖铺满客厅地面,需要多少块这样的地砖?(注意:在答题卡上写完答案后,还要将你的思考过程在答题卡的图中表示出来.)
(2)小明想在墙壁上画一个图形作为装饰,这个图形刚好占7个小方格.请你在如图3中帮他完成这个设计.
考点11 运用平移、对称和旋转设计图案
点拨:(1)如图,正方形的一边用3快长方形地砖的长正好铺完,另一相邻边用4快长方形地砖的宽正好铺完,这样一共要用3×4=12(块).
(2)根据轴对称即可设计出这个装饰图形,正好是7个方格.
解:(1)3×4=12(块)
答:需要多少块这样的地砖(如图).
(2)帮助小明设计装饰图如图:
课后作业
1.完成讲义真题训练;
2.复习本讲错题。
第六单元
平移、旋转和轴对称
期末考点集训
2023-2024学年苏教版数学三年级上册
知识解读
知识点01:平移和旋转
1.平移:物体或图形沿着直线做运动
2.旋转:一个物体或图形绕着一个点或一个轴转动的现象。
3.平移和旋转都是物体或图形运动的现象,运动中物体的形状和大小都不变;二者的区别在于:平移是物体做直线运动,而旋转是物体绕一个点或轴转动,平移只改变位置,旋转改变的是方向和位置。
知识点02:轴对称图形
1.轴对称图形:把一个图形沿着某一条直线对折,对折后折痕两侧的部分能完全重合,这样的图形就是轴对称图形。折痕所在的直线是图形的对称轴。
2.轴对称图形的特征:对折后,对称轴两侧能完全重合。
易错点01:平移和旋转
1. 判断平移现象时,要看物体是不是沿直线运动。
2. 物体绕着某一个点运动就是旋转,不一定要转动一周。
易错点02:轴对称图形
1.轴对称图形沿对称轴对折后,两边能够完全重合。
易错点拨
考点目录
【考点01】轴对称的概念
【考点02】确定轴对称图形的对称轴条数及位置
【考点03】作轴对称图形
【考点04】画轴对称图形的对称轴
【考点05】画轴对称图形的对称轴
【考点06】镜面对称
【考点07】平移的概念
【考点08】作平移后的图形
【考点09】旋转的概念
【考点10】作旋转一定角度后的图形
【考点11】运用平移、对称和旋转设计图案
考点精讲练
【典例精讲】(2020秋 睢宁县期末)按如图的图案剪一个轴对称图形,展开后是( )
考点01 轴对称的概念
点拨:轴对称:在平面内,如果一个图形沿一条直线对折,对折后的两部分都能完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴。
解:按如图的图案剪一个轴对称图形,展开后是 。
故选:A。
考点精讲练
【真题强化】(2020秋 东海县校级月考)下面的图案各是从哪张纸上剪下来的?连一连。
考点01 轴对称的概念
点拨:依据轴对称图形的概念,即在平面内,如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴,据此解答即可。
解:
考点精讲练
【典例精讲】(2023秋 庆云县期中)下面图形中,对称轴条数最少的是( )
A. B. C. D.
考点02 确定轴对称图形的对称轴条数及位置
点拨:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴,据此数出它们的对称轴,即可选择。
解:上面图形中,对称轴条数最少的是 , 有3条对称轴; 有4条对称轴, 有无数条对称轴。
故选:D。
考点精讲练
【真题强化】(2023秋 岷县期中)如图所示是轴对称图形的有( )个.
A.1 B.2 C.3 D.4
考点02 确定轴对称图形的对称轴条数及位置
点拨:根据轴对称图形的概念:一个图形沿某条直线对折,直线两旁的部分能够完全重合,这个图形就是轴对称图形,由此对各图形分析判断后即可求解.
解:图1是轴对称图形,图2不是轴对称图形;图3是轴对称图形;图4是轴对称图形;图5不轴对称图形,
所以一共有3个图形是轴对称图形.
故选:C.
考点精讲练
【典例精讲】(2023春 离石区期末)如图是一些国家的国旗,其中是轴对称图形的有( )
A.4个 B.3个 C.2个 D.1个
考点03 轴对称图形的辨识
点拨:根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;依次进行判断即可.
解:根据轴对称图形的意义可知:加拿大、摩洛哥、瑞典的国旗都是轴对称图形,而澳大利亚的国旗不是轴对称图形;
故选:B.
考点精讲练
【真题强化】(2021秋 广平县期末)是轴对称图形的画“√”,不是轴对称图形的在括号里画“×”。
考点03 轴对称图形的辨识
点拨:轴对称:在平面内,如果一个图形沿一条直线对折,对折后的两部分都能完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴
解:
考点精讲练
【典例精讲】(2021秋 如东县期末)如图是用边长1厘米的小正方形拼成。图中涂色部分占整个图形的 ,涂色部分的周长是 厘米。想象一下,把涂色部分去掉一格,使得剩下的涂色部分变成一个轴对称图形,有 种不同的方法。
考点04 作轴对称图形
点拨:把整个长方形的面积看作一个整体,把它平均分成8份,每份是它的 ,其中5份涂色,表示 ;求涂色部分的周长,可能数格的方法数出;把涂色部分去掉一格,使得剩下的涂色部分变成一个轴对称图形,可去掉第一行的或去掉下行右边一个,即有2种不同的方法。
解:用边长1厘米的小正方形拼成。图中涂色部分占整个图形的 ,涂色部分的周长是12厘米。想象一下,把涂色部分去掉一格,使得剩下的涂色部分变成一个轴对称图形,有2种不同的方法。
故答案为:,12,2。
考点精讲练
【真题强化】(2023秋 宿州月考)按要求做。
(1)画出图①中图形的对称轴。
(2)在图②已知图形的基础上再涂2格,使涂色部分成为轴对称图形。
考点04 作轴对称图形
点拨:(1)根据轴对称图形的特征,如果一个图形沿着一条直线打折,左右完全重合,这个图形就是轴对称图形,这条直线就是对称轴。据此作图即可。
(2)根据轴对称图形的特征,如果一个图形沿着一条直线打折,左右完全重合,这个图形就是轴对称图形,这条直线就是对称轴。据此作图即可。(答案不唯一)
解:(1)画出图①中图形的对称轴。作图如下:
(2)在图②已知图形的基础上再涂2格,使涂色部分成为轴对称图形。作图如下:
(答案不唯一)
考点精讲练
【典例精讲】(2023秋 榕城区期中)在如图中,再选3格涂色,使它们构成一幅轴对称图形,并画出它的对称轴。
考点05 画轴对称图形的对称轴
点拨:如果一个图形沿着一条直线折叠后,直线两旁的部分能够完全重合,那么这个图形就叫作轴对称图形,折痕所在的直线就是对称轴,再选择3格涂上颜色,使它们构成一幅轴对称图形即可。
解:作图如下:
(画法不唯一,合理即可)
考点精讲练
【真题强化】(2021秋 威县期末)描一描,画一画。
(1)用彩笔描出下面图形的周长。
(2)在下面轴对称图形中画出一条对称轴。
考点05 画轴对称图形的对称轴
点拨:(1)根据周长的含义:物体的边缘或围成平面图形一周的长,叫做它的周长;由此用彩笔沿图形的一周描出图形的周长即可;
(2)根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;据此判断,然后画出一条对称轴即可。
解:(1) (2)
考点精讲练
【典例精讲】(2021秋 福鼎市期末)小明看到河边的岸上有一座房子的形状如图,那么他看到房子在水中的倒影应该是( )
A. B.
C. D.
考点06 镜面对称
点拨:根据镜面对称的特征,镜中的景物与实际景物上下前后方向一致,左右方向相反,大小不变,且关于镜面对称。
解:根据分析可知,房子和它的倒影是以水面为对称轴的轴对称图形。
故选:D。
考点精讲练
【真题强化】(2019秋 观山湖区期末)如图是从镜中看到的一串数字,这串数字应为 .
考点06 镜面对称
点拨:根据镜面对称的性质求解,在平面镜中的像与现实中的事物恰好左右顺序颠倒,且关于镜面对称.
解:如图 是从镜中看到的一串数字,这串数字应为810076;
故答案为:810076.
考点精讲练
【典例精讲】(2023秋 礼泉县期中)如图,图形甲( )才能将最下面一行填满。
A.先向右平移2格,再向下平移2格
B.先向右平移3格,再向下平移2格
C.先向右平移3格,再向下平移3格
D.先向右平移2格,再向下平移3格
考点07 平移的概念
点拨:平移是物体运动时,物体上任意两点间,从一点到另一点的方向与距离都不变的运动,平移后图形的位置改变,形状、大小不变;据此解答即可。
解:如图,图形甲先向右平移3格,再向下平移3格才能将最下面一行填满。
故选:C。
考点精讲练
【真题强化】(2023春 吉利区期末)如图,由图A到图B是向 平移了 格,由图B到图C是向 平移了 格.
考点07 平移的概念
点拨:根据图中两图的相对距离及箭头指向即可确定平移的方向和距离,所以图A到图B是向 右平移了 6格,由图B到图C是向 下平移了 2格;由此解答即可.
解:如图,由图A到图B是向 右平移了 6格,由图B到图C是向 下平移了 2格.
故答案为:右,6,下,2.
考点精讲练
【典例精讲】(2023秋 礼泉县期中)(1)以虚线为对称轴,点P的对称点是点 。
(2)图形甲先向下平移 格,再向右平移 格可以得到图形乙。
考点08 作平移后的图形
点拨:(1)根据对称的意义,即可解答;(2)找准方向,数清格数,即可解答。
解:(1)以虚线为对称轴,点P的对称点是点B。
(2)图形甲先向下平移3格,再向右平移5格可以得到图形乙。
故答案为:B;3,5。
考点精讲练
【真题强化】(2023秋 滕州市期中)图一中左侧的图形先向 平移 格,再向 平移 格就得到右侧的图形。图二中左侧的图形先向 平移 格,再向 平移 格就得到右侧的图形。
考点08 作平移后的图形
点拨:确定平移后图形的基本要素有两个:平移方向、平移距离,结合题意分析分析解答即可。
解:图一中左侧的图形先向下平移2格,再向右平移3格就得到右侧的图形。图二中左侧的图形先向上平移3格,再向右平移3格就得到右侧的图形。
故答案为:下,2,右,3,上,3,右,3。
考点精讲练
【典例精讲】(2023秋 项城市期中)如图,从12:00到3:00,时针沿顺时针方向旋转了( )°。
A.90 B.60 C.180
考点09 旋转的概念
点拨:钟面上12个数字,以表芯为旋转点,表针转一圈是360°,被12个数字平均分成12份,每一份也就是两数之间夹角是30°;从12:00到3:00,时针沿顺时针方向旋转了3大格,是3×30°=90°。据此解答即可。
解:3×30°=90°
答:从12:00到3:00,时针沿顺时针方向旋转了90°。
故选:A。
考点精讲练
【真题强化】(2023秋 沈丘县期中)(1)图形①绕点O沿逆时针方向旋转 ,得到图形④。
(2)图形②绕点O沿 时针方向旋转90°,得到图形③。
(3)图形①可以看作是图形 沿逆时针方向旋转90°得到的,还可以看作是图形 沿顺时针方向旋转90°得到的。
考点09 旋转的概念
点拨:根据旋转知识,先确定旋转的中心,再观察是按顺时针方向旋转,还是按逆时针方向旋转,最后确定旋转的度数即可。
解:(1)图形①绕点O沿逆时针方向旋转90°,得到图形④。
(2)图形②绕点O沿顺时针方向旋转90°,得到图形③。
(3)图形①可以看作是图形②沿逆时针方向旋转90°得到的,还可以看作是图形④沿顺时针方向旋转90°得到的。
故答案为:90;顺;②,④。
考点精讲练
【典例精讲】(2023 朝阳区模拟)图形A经过( )运动后可变成图形B。
A.绕Q点逆时针旋转90°,再向下平移2格
B.绕Q点顺时针旋转90°,再向下平移2格
C.绕P点逆时针旋转90°,再向右平移2格
考点10 作旋转一定角度后的图形
点拨:根据图形的旋转和平移知识,图形A经过绕Q点顺时针旋转90°,再向下平移2格运动后可变成图形B,据此解答即可。
解:图形A经过绕Q点顺时针旋转90°,再向下平移2格运动后可变成图形B。
故选:B。
考点精讲练
【真题强化】(2023秋 庆云县期中)按要求画一画。
①画出梯形绕A点顺时针旋转90°后的图形。
②把平行四边形向右平移6格,画出平移后的图形。
③把如图所示图形补全,使它成为一个轴对称图形。
考点10 作旋转一定角度后的图形
点拨:①根据旋转的特征,梯形绕点A顺时针旋转90°,点A的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形;
②根据平移的特征,把平行四边形的各顶点分别向向右平移6格,依次连接即可得到平移后的图形;
③根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴(虚线)的下边画上半左图的关键对称点,依次连接即可。
解:根据题意画图如下:
考点精讲练
【典例精讲】(2019秋 玉门市期末)请按照给出的对称轴画出第一个图形的对称图形,第二个图形请向上移动3格.
考点11 运用平移、对称和旋转设计图案
点拨:按照给出的对称轴画出第一个图形的对称图形:找出5个关键点(图形中的顶点)关于对称轴的对称点,连接这5个对称点,填充黑色,即可得解.
第二个图形向上移动3格,找出5个关键点(图形中的顶点)向上移动3格,连接这5个端点,填充黑色,即可得解.
解:作图如上:
考点精讲练
【真题强化】(1)小明家的客厅地面是一个正方形,如图1.要用图2所示的长方形地砖铺满客厅地面,需要多少块这样的地砖?(注意:在答题卡上写完答案后,还要将你的思考过程在答题卡的图中表示出来.)
(2)小明想在墙壁上画一个图形作为装饰,这个图形刚好占7个小方格.请你在如图3中帮他完成这个设计.
考点11 运用平移、对称和旋转设计图案
点拨:(1)如图,正方形的一边用3快长方形地砖的长正好铺完,另一相邻边用4快长方形地砖的宽正好铺完,这样一共要用3×4=12(块).
(2)根据轴对称即可设计出这个装饰图形,正好是7个方格.
解:(1)3×4=12(块)
答:需要多少块这样的地砖(如图).
(2)帮助小明设计装饰图如图:
课后作业
1.完成讲义真题训练;
2.复习本讲错题。
同课章节目录
