苏教版四年级下册数学7.2 三角形的三边关系(课件)(共35张PPT)
文档属性
| 名称 | 苏教版四年级下册数学7.2 三角形的三边关系(课件)(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 00:00:00 | ||
图片预览





文档简介
(共35张PPT)
第七单元 三角形、平行四边形和梯形
三角形的三边关系
苏教版四年级下册数学
通过直观操作活动和计算观察,让学生探索并发现三角形任意两边长度的和大于第三边。
引导学生参与探究和发现活动,经历操作、发现、验证的探究过程,培养学生自主探究、合作交流的能力。
培养学生积极的学习态度和乐于探究的数学情感。
回忆一下,关于三角形,我们已经获得了哪些认识呢?在小组里说说,汇总一下,请组长汇报吧!
三条线段首尾相接围成的图形叫作三角形。
三角形有3条边、3个顶点、3个角。三角形中存在底和高的对应关系。
我们研究过三角形的三边关系:三角形任意两边长度的和大于第三边。
今天我们来研究三角形的内角和。
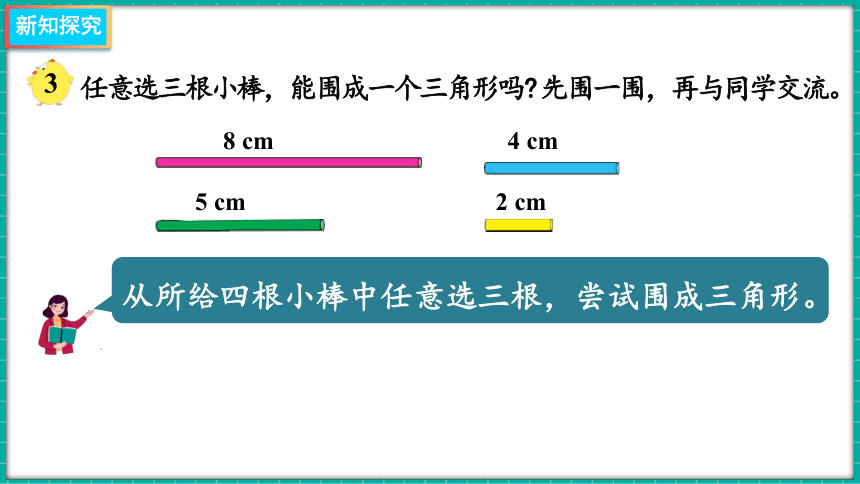
8 cm
4 cm
2 cm
5 cm
3
任意选三根小棒,能围成一个三角形吗 先围一围,再与同学交流。
从所给四根小棒中任意选三根,尝试围成三角形。
3
任意选三根小棒,能围成一个三角形吗 先围一围,再与同学交流。
8 cm
4 cm
2 cm
5 cm
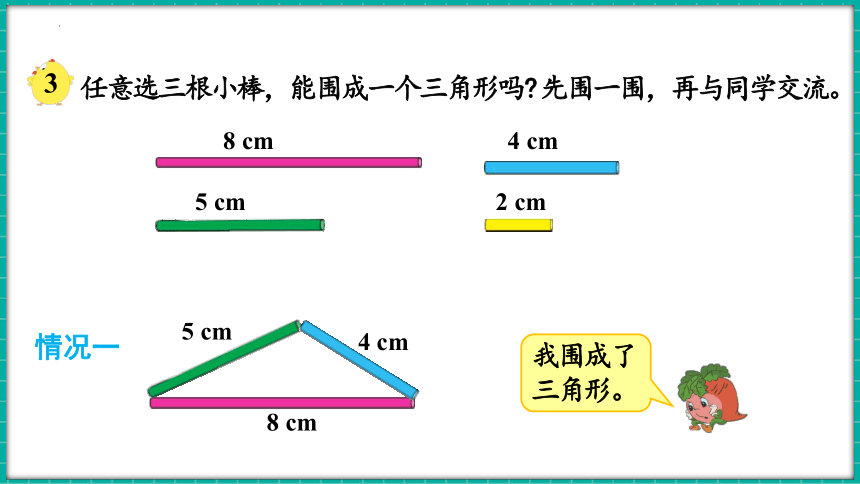
情况一
我围成了三角形。
8 cm
5 cm
4 cm
3
任意选三根小棒,能围成一个三角形吗 先围一围,再与同学交流。
8 cm
4 cm
2 cm
5 cm
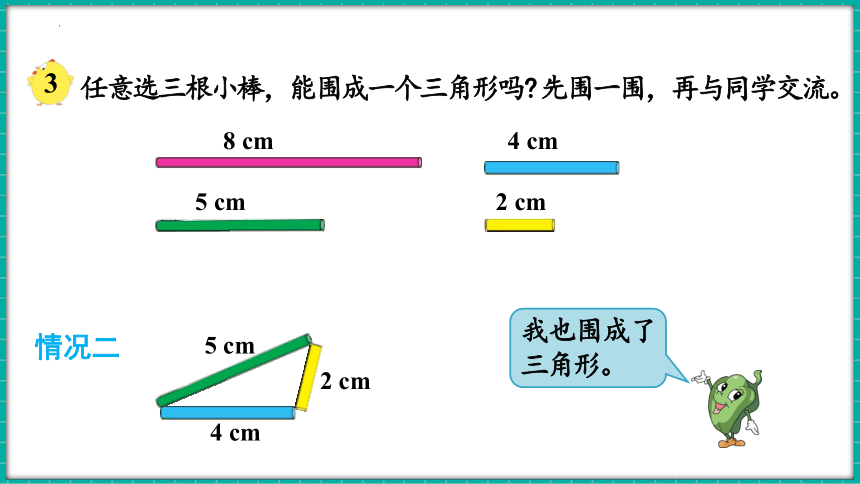
情况二
5 cm
4 cm
2 cm
我也围成了三角形。
3
任意选三根小棒,能围成一个三角形吗 先围一围,再与同学交流。
8 cm
4 cm
2 cm
5 cm
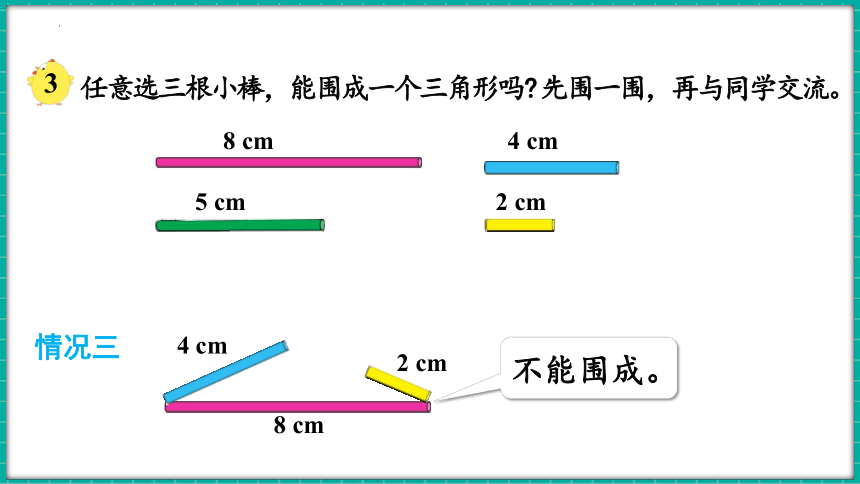
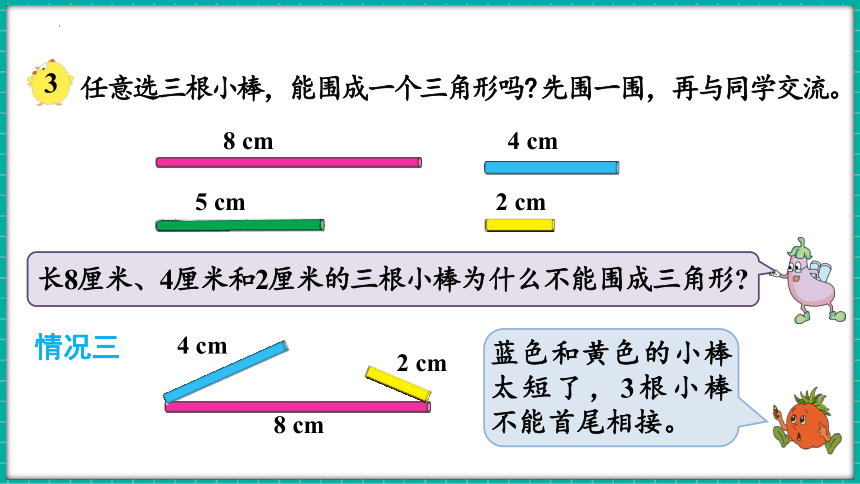
情况三
不能围成。
8 cm
4 cm
2 cm
3
任意选三根小棒,能围成一个三角形吗 先围一围,再与同学交流。
8 cm
4 cm
2 cm
5 cm
情况三
8 cm
4 cm
2 cm
长8厘米、4厘米和2厘米的三根小棒为什么不能围成三角形
蓝色和黄色的小棒太短了,3根小棒不能首尾相接。
3
任意选三根小棒,能围成一个三角形吗 先围一围,再与同学交流。
8 cm
4 cm
2 cm
5 cm
情况三
8 cm
4 cm
2 cm
长8厘米、4厘米和2厘米的三根小棒为什么不能围成三角形
4厘米 + 2厘米< 8厘米,所以不能围成三角形。
3
任意选三根小棒,能围成一个三角形吗 先围一围,再与同学交流。
8 cm
4 cm
2 cm
5 cm
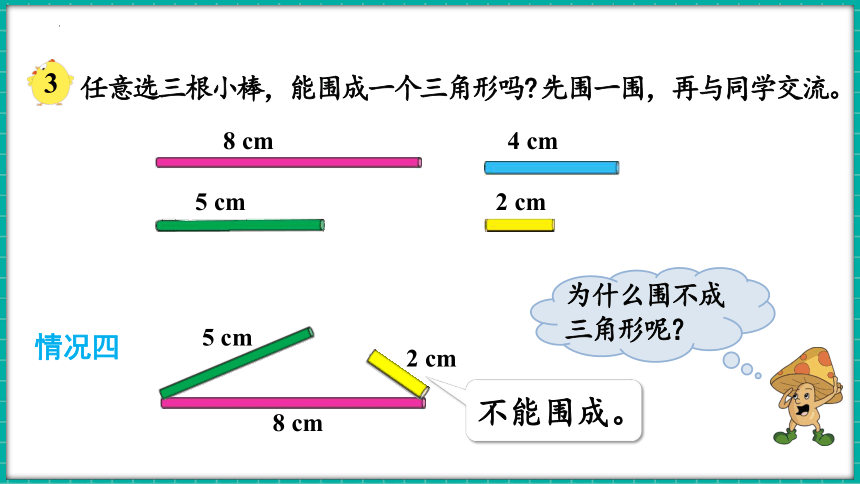
情况四
不能围成。
为什么围不成三角形呢?
8 cm
2 cm
5 cm
3
任意选三根小棒,能围成一个三角形吗 先围一围,再与同学交流。
8 cm
4 cm
2 cm
5 cm
情况四
8 cm
2 cm
5 cm
长8厘米、5厘米和2厘米的三根小棒为什么不能围成三角形
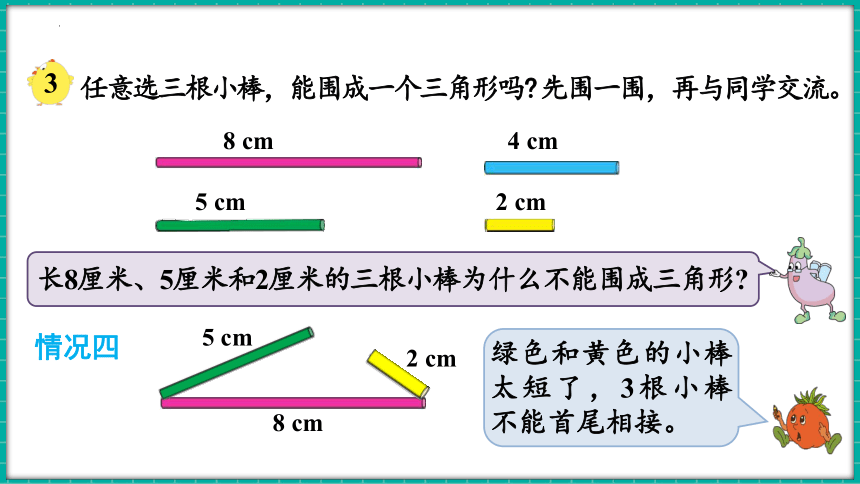
绿色和黄色的小棒太短了,3根小棒不能首尾相接。
3
任意选三根小棒,能围成一个三角形吗 先围一围,再与同学交流。
8 cm
4 cm
2 cm
5 cm
情况四
8 cm
2 cm
5 cm
长8厘米、5厘米和2厘米的三根小棒为什么不能围成三角形
5厘米 + 2厘米< 8厘米,所以不能围成三角形。
为什么有的围的起来,有的围不起来呢?
记录一下所有你围成的边长情况,分析交流一下吧!
有思路了吗?我们把它再列个表,就更清楚了。
8 cm
5 cm
4 cm
5 cm
4 cm
2 cm
8 cm
4 cm
2 cm
8 cm
2 cm
5 cm
不能围成三角形的三根小棒长度之间的关系
围成的图形 直观来看 比较三根小棒长度之间的关系 发现
蓝色和黄色的小棒太短了,3根小棒不能首尾相接。
4 + 2 < 8
8 + 2 > 4
8 + 4 > 2
绿色和黄色的小棒太短了,3根小棒不能首尾相接。
5 + 2 < 8
8 + 2 > 5
8 + 5 > 2
较短的两根小棒的长度和小于第三根小棒的长度时,不能围成三角形。
能围成三角形的三根小棒长度之间的关系
从围成三角形的三根小棒中任意选出两根,将它们的长度和与第三根比较,结果怎样?
能围成三角形的三根小棒长度之间的关系
围成的图形 比较三根小棒长度之间的关系 发现
4 + 5 > 8
4 + 8 > 5
5 + 8 > 4
4 + 2 > 5
4 + 5 > 2
5 + 2 > 4
任意两根小棒的长度和都大于第三根小棒的长度时,能围成三角形。
任意两根小棒的长度和一定大于第三根小棒。
探究三角形的三边关系
三角形任意两边长度的和一定大于第三边吗?先画一个三角形, 再量一量、 算一算。
6 cm
7 cm
8 cm
6+7>8
8+11>11
8+7>6
8+6>7
11+11>8
8 cm
11 cm
11 cm
三角形任意两边长度的和大于第三边
如果三根小棒的长度分别是8厘米、5厘米和3厘米,能围成三角形吗?为什么?
3 cm
5 cm
8 cm
3 cm
5 cm
8 cm
3+5=8
3个顶点在同一条直线上,而围成三角形的3个顶点不能在同一条直线上,所以这样的三根小棒不能围成一个三角形。
三角形任意两边长度的和真的是一定大于第三边吗?每位同学都来试试,先画一个三角形,再量一量、算一算,看看有没有能推翻这个结论的“例子”!
验证结论:三角形任意两边长度的和大于第三边。
下面哪组线段可以围成一个三角形?为什么?
1
2+4=6
2+2<5
2+5>6
2+6>5
5+6>2
2
一个三角形,两边的长分别是12厘米和18厘米,第三边的长可能是多少厘米 在合适的答案下面画“√”。
第三边
两边之差 <
< 两边之和
5厘米 25厘米 30厘米 38厘米
18-12=6
18+12=30
√
3根同样长的小棒,能否首尾相连地摆成一个三角形?
试试看,并尝试说明理由。
1
每条边的长度都是a,
则有a+a>a,所以一定可以。
a
4根同样长的小棒,能否首尾相连地摆成一个三角形 (其中2根小棒可以摆成三角形的一条边)
a
每条边的长度都是a,
则有a+a=2a,所以一定不可以。
2
3
有两根长度分别为2 cm和5 cm的小棒,如果要摆成一个三角形,第三条边选用小棒的长度范围应是什么?先想一想,再根据你的答案摆一摆。
第三边既要“大于两边之差”,又要“小于两边之和”。所以,所选小棒的长度只要大于3厘米,小于7厘米,均可。
第三边
两边之差 <
< 两边之和
5-2=3
5+2=7
a
b
c
4
从学校到少年宫有几条路线?走哪一条路线比较近?
答:共有2条路线。直接走路线c最近,因为“三角形的任意两边长度之和大于第三边”。
5
算一算,再填空。
两根小棒分别长4厘米、7厘米,第三根小棒的长度要小于( )厘米且大于3厘米,这3根小棒才能才能围成一个三角形。
4+7=11(厘米)
11
一个三角形的周长是10厘米,三条边的长度均为整厘米数。其中一边长度为4厘米,其余两条边的长度可以是( )厘米和( )厘米;也可以是( )厘米和( )厘米。
2
4
3
3
5
算一算,再填空。
6
用一根长24厘米的铁丝围成一个三角形,这个三角形的最长边长度必须要小于多少厘米呢?
应用“两边之和大于第三边”
24÷2=12(厘米)
答:这条最长的边长度必须要小于12厘米。
点A到点B之间线段的长度,就是点A到点B之间的距离。
两根小棒重合时,A、B两点之间的距离最短。
如下图,把两根小棒的一端固定,做成一个可以自由开合的
木夹,点A到点B之间的距离最短是多少厘米?
11cm
B
A
7cm
11 – 7 = 4 (cm)
答:点A到点B之间的距离最短是4厘米。
7
从长度分别为2 cm、4 cm、5 cm、8 cm的四根小棒中任意
选取3根小棒,能摆成几个三角形?
三角形任意两边的和大于第三边。
可以先列举出所有可能的组合方法,再分别考虑能否摆成三角形。
8
共有四种组合方法:
(1)2 cm、4 cm、5 cm
(2)2 cm、4 cm、8 cm
(3)2 cm、5 cm、8 cm
(4)4 cm、5 cm、8 cm
能摆成三角形
能摆成三角形
不能摆成三角形
不能摆成三角形
答:最多能摆成2个三角形。
2+4<8
2+5<8
这节课你有什么收获?
三角形的三边关系
1.三角形任意两边长度的和大于第三边。
2.判断3条线段能否围成三角形,只需要判
断两条短边的和是否大于第三边,如果
大于就能围成三角形,反之则不能。
课堂小结
第七单元 三角形、平行四边形和梯形
三角形的三边关系
苏教版四年级下册数学
通过直观操作活动和计算观察,让学生探索并发现三角形任意两边长度的和大于第三边。
引导学生参与探究和发现活动,经历操作、发现、验证的探究过程,培养学生自主探究、合作交流的能力。
培养学生积极的学习态度和乐于探究的数学情感。
回忆一下,关于三角形,我们已经获得了哪些认识呢?在小组里说说,汇总一下,请组长汇报吧!
三条线段首尾相接围成的图形叫作三角形。
三角形有3条边、3个顶点、3个角。三角形中存在底和高的对应关系。
我们研究过三角形的三边关系:三角形任意两边长度的和大于第三边。
今天我们来研究三角形的内角和。
8 cm
4 cm
2 cm
5 cm
3
任意选三根小棒,能围成一个三角形吗 先围一围,再与同学交流。
从所给四根小棒中任意选三根,尝试围成三角形。
3
任意选三根小棒,能围成一个三角形吗 先围一围,再与同学交流。
8 cm
4 cm
2 cm
5 cm
情况一
我围成了三角形。
8 cm
5 cm
4 cm
3
任意选三根小棒,能围成一个三角形吗 先围一围,再与同学交流。
8 cm
4 cm
2 cm
5 cm
情况二
5 cm
4 cm
2 cm
我也围成了三角形。
3
任意选三根小棒,能围成一个三角形吗 先围一围,再与同学交流。
8 cm
4 cm
2 cm
5 cm
情况三
不能围成。
8 cm
4 cm
2 cm
3
任意选三根小棒,能围成一个三角形吗 先围一围,再与同学交流。
8 cm
4 cm
2 cm
5 cm
情况三
8 cm
4 cm
2 cm
长8厘米、4厘米和2厘米的三根小棒为什么不能围成三角形
蓝色和黄色的小棒太短了,3根小棒不能首尾相接。
3
任意选三根小棒,能围成一个三角形吗 先围一围,再与同学交流。
8 cm
4 cm
2 cm
5 cm
情况三
8 cm
4 cm
2 cm
长8厘米、4厘米和2厘米的三根小棒为什么不能围成三角形
4厘米 + 2厘米< 8厘米,所以不能围成三角形。
3
任意选三根小棒,能围成一个三角形吗 先围一围,再与同学交流。
8 cm
4 cm
2 cm
5 cm
情况四
不能围成。
为什么围不成三角形呢?
8 cm
2 cm
5 cm
3
任意选三根小棒,能围成一个三角形吗 先围一围,再与同学交流。
8 cm
4 cm
2 cm
5 cm
情况四
8 cm
2 cm
5 cm
长8厘米、5厘米和2厘米的三根小棒为什么不能围成三角形
绿色和黄色的小棒太短了,3根小棒不能首尾相接。
3
任意选三根小棒,能围成一个三角形吗 先围一围,再与同学交流。
8 cm
4 cm
2 cm
5 cm
情况四
8 cm
2 cm
5 cm
长8厘米、5厘米和2厘米的三根小棒为什么不能围成三角形
5厘米 + 2厘米< 8厘米,所以不能围成三角形。
为什么有的围的起来,有的围不起来呢?
记录一下所有你围成的边长情况,分析交流一下吧!
有思路了吗?我们把它再列个表,就更清楚了。
8 cm
5 cm
4 cm
5 cm
4 cm
2 cm
8 cm
4 cm
2 cm
8 cm
2 cm
5 cm
不能围成三角形的三根小棒长度之间的关系
围成的图形 直观来看 比较三根小棒长度之间的关系 发现
蓝色和黄色的小棒太短了,3根小棒不能首尾相接。
4 + 2 < 8
8 + 2 > 4
8 + 4 > 2
绿色和黄色的小棒太短了,3根小棒不能首尾相接。
5 + 2 < 8
8 + 2 > 5
8 + 5 > 2
较短的两根小棒的长度和小于第三根小棒的长度时,不能围成三角形。
能围成三角形的三根小棒长度之间的关系
从围成三角形的三根小棒中任意选出两根,将它们的长度和与第三根比较,结果怎样?
能围成三角形的三根小棒长度之间的关系
围成的图形 比较三根小棒长度之间的关系 发现
4 + 5 > 8
4 + 8 > 5
5 + 8 > 4
4 + 2 > 5
4 + 5 > 2
5 + 2 > 4
任意两根小棒的长度和都大于第三根小棒的长度时,能围成三角形。
任意两根小棒的长度和一定大于第三根小棒。
探究三角形的三边关系
三角形任意两边长度的和一定大于第三边吗?先画一个三角形, 再量一量、 算一算。
6 cm
7 cm
8 cm
6+7>8
8+11>11
8+7>6
8+6>7
11+11>8
8 cm
11 cm
11 cm
三角形任意两边长度的和大于第三边
如果三根小棒的长度分别是8厘米、5厘米和3厘米,能围成三角形吗?为什么?
3 cm
5 cm
8 cm
3 cm
5 cm
8 cm
3+5=8
3个顶点在同一条直线上,而围成三角形的3个顶点不能在同一条直线上,所以这样的三根小棒不能围成一个三角形。
三角形任意两边长度的和真的是一定大于第三边吗?每位同学都来试试,先画一个三角形,再量一量、算一算,看看有没有能推翻这个结论的“例子”!
验证结论:三角形任意两边长度的和大于第三边。
下面哪组线段可以围成一个三角形?为什么?
1
2+4=6
2+2<5
2+5>6
2+6>5
5+6>2
2
一个三角形,两边的长分别是12厘米和18厘米,第三边的长可能是多少厘米 在合适的答案下面画“√”。
第三边
两边之差 <
< 两边之和
5厘米 25厘米 30厘米 38厘米
18-12=6
18+12=30
√
3根同样长的小棒,能否首尾相连地摆成一个三角形?
试试看,并尝试说明理由。
1
每条边的长度都是a,
则有a+a>a,所以一定可以。
a
4根同样长的小棒,能否首尾相连地摆成一个三角形 (其中2根小棒可以摆成三角形的一条边)
a
每条边的长度都是a,
则有a+a=2a,所以一定不可以。
2
3
有两根长度分别为2 cm和5 cm的小棒,如果要摆成一个三角形,第三条边选用小棒的长度范围应是什么?先想一想,再根据你的答案摆一摆。
第三边既要“大于两边之差”,又要“小于两边之和”。所以,所选小棒的长度只要大于3厘米,小于7厘米,均可。
第三边
两边之差 <
< 两边之和
5-2=3
5+2=7
a
b
c
4
从学校到少年宫有几条路线?走哪一条路线比较近?
答:共有2条路线。直接走路线c最近,因为“三角形的任意两边长度之和大于第三边”。
5
算一算,再填空。
两根小棒分别长4厘米、7厘米,第三根小棒的长度要小于( )厘米且大于3厘米,这3根小棒才能才能围成一个三角形。
4+7=11(厘米)
11
一个三角形的周长是10厘米,三条边的长度均为整厘米数。其中一边长度为4厘米,其余两条边的长度可以是( )厘米和( )厘米;也可以是( )厘米和( )厘米。
2
4
3
3
5
算一算,再填空。
6
用一根长24厘米的铁丝围成一个三角形,这个三角形的最长边长度必须要小于多少厘米呢?
应用“两边之和大于第三边”
24÷2=12(厘米)
答:这条最长的边长度必须要小于12厘米。
点A到点B之间线段的长度,就是点A到点B之间的距离。
两根小棒重合时,A、B两点之间的距离最短。
如下图,把两根小棒的一端固定,做成一个可以自由开合的
木夹,点A到点B之间的距离最短是多少厘米?
11cm
B
A
7cm
11 – 7 = 4 (cm)
答:点A到点B之间的距离最短是4厘米。
7
从长度分别为2 cm、4 cm、5 cm、8 cm的四根小棒中任意
选取3根小棒,能摆成几个三角形?
三角形任意两边的和大于第三边。
可以先列举出所有可能的组合方法,再分别考虑能否摆成三角形。
8
共有四种组合方法:
(1)2 cm、4 cm、5 cm
(2)2 cm、4 cm、8 cm
(3)2 cm、5 cm、8 cm
(4)4 cm、5 cm、8 cm
能摆成三角形
能摆成三角形
不能摆成三角形
不能摆成三角形
答:最多能摆成2个三角形。
2+4<8
2+5<8
这节课你有什么收获?
三角形的三边关系
1.三角形任意两边长度的和大于第三边。
2.判断3条线段能否围成三角形,只需要判
断两条短边的和是否大于第三边,如果
大于就能围成三角形,反之则不能。
课堂小结
