数学人教A版(2019)必修第一册4.1.2无理数指数幂及其运算性质(共16张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册4.1.2无理数指数幂及其运算性质(共16张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-21 17:03:43 | ||
图片预览





文档简介
(共16张PPT)
第
四
指数函数与对数函数
章
4.1.2 无理数指数幂及其运算性质
理解无理数指数幂的含义,掌握其运算性质.
学习目标
准备好了吗?一起去探索吧!
掌握无理数指数幂的运算性质,并能对代数式进行化简或求值.
掌握实数指数幂的综合运用.
难点
重点
掌握实数指数幂的综合运用.
无理数指数幂的概念及其运算性质.
在初中的学习中,我们通过有理数认识了一些无理数.
类似地,也可以通过有理数指数幂来认识无理数指数幂.
x的取值范围从整数拓展到了
有理数,那么,当指数x是无理数时,的意义是什么?
它是一个确定的数吗?如果是,它有怎样的运算性质?
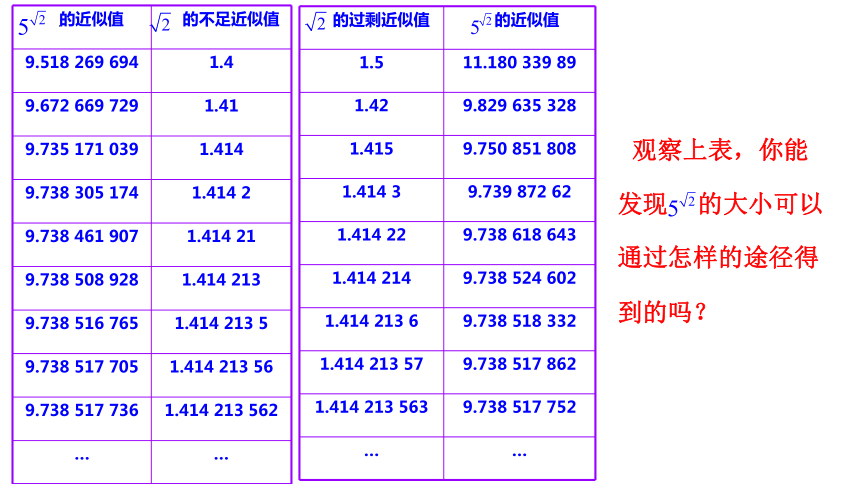
思考:观察下表, 是否表示一个确定的实数?
的近似值 的不足近似值
9.518 269 694 1.4
9.672 669 729 1.41
9.735 171 039 1.414
9.738 305 174 1.414 2
9.738 461 907 1.414 21
9.738 508 928 1.414 213
9.738 516 765 1.414 213 5
9.738 517 705 1.414 213 56
9.738 517 736 1.414 213 562
… …
的过剩近似值 的近似值
1.5 11.180 339 89
1.42 9.829 635 328
1.415 9.750 851 808
1.414 3 9.739 872 62
1.414 22 9.738 618 643
1.414 214 9.738 524 602
1.414 213 6 9.738 518 332
1.414 213 57 9.738 517 862
1.414 213 563 9.738 517 752
… …
观察上表,你能发现 的大小可以通过怎样的途径得到的吗?
结论: 是由一串逐渐增大的有理指数幂的值
、、、,……
和另一串逐渐减小的有理指数幂的值
、、、,…… 无限逼近的结果,它是一个确定的实数
.
练一练
√
√
例1
迁移
1.整体代换法是计算常用的方法技巧,分析条件与结论的结构特点,灵活运用恒等式是解题关键.在利用整体代换法解决分数指数幂的计算问题时,常用完全平方式及变形公式求解.
2.本例中也可利用方程思想求xα,代入求值.
思考:本节课都学了什么?
训练3
第
四
指数函数与对数函数
章
4.1.2 无理数指数幂及其运算性质
理解无理数指数幂的含义,掌握其运算性质.
学习目标
准备好了吗?一起去探索吧!
掌握无理数指数幂的运算性质,并能对代数式进行化简或求值.
掌握实数指数幂的综合运用.
难点
重点
掌握实数指数幂的综合运用.
无理数指数幂的概念及其运算性质.
在初中的学习中,我们通过有理数认识了一些无理数.
类似地,也可以通过有理数指数幂来认识无理数指数幂.
x的取值范围从整数拓展到了
有理数,那么,当指数x是无理数时,的意义是什么?
它是一个确定的数吗?如果是,它有怎样的运算性质?
思考:观察下表, 是否表示一个确定的实数?
的近似值 的不足近似值
9.518 269 694 1.4
9.672 669 729 1.41
9.735 171 039 1.414
9.738 305 174 1.414 2
9.738 461 907 1.414 21
9.738 508 928 1.414 213
9.738 516 765 1.414 213 5
9.738 517 705 1.414 213 56
9.738 517 736 1.414 213 562
… …
的过剩近似值 的近似值
1.5 11.180 339 89
1.42 9.829 635 328
1.415 9.750 851 808
1.414 3 9.739 872 62
1.414 22 9.738 618 643
1.414 214 9.738 524 602
1.414 213 6 9.738 518 332
1.414 213 57 9.738 517 862
1.414 213 563 9.738 517 752
… …
观察上表,你能发现 的大小可以通过怎样的途径得到的吗?
结论: 是由一串逐渐增大的有理指数幂的值
、、、,……
和另一串逐渐减小的有理指数幂的值
、、、,…… 无限逼近的结果,它是一个确定的实数
.
练一练
√
√
例1
迁移
1.整体代换法是计算常用的方法技巧,分析条件与结论的结构特点,灵活运用恒等式是解题关键.在利用整体代换法解决分数指数幂的计算问题时,常用完全平方式及变形公式求解.
2.本例中也可利用方程思想求xα,代入求值.
思考:本节课都学了什么?
训练3
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
