5.4抛体运动的规律课件(17张PPT)高一下学期物理人教版(2019)必修第二册
文档属性
| 名称 | 5.4抛体运动的规律课件(17张PPT)高一下学期物理人教版(2019)必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-12-21 09:47:46 | ||
图片预览






文档简介
(共17张PPT)
按题意作图,求得分速度后就可以求得夹角θ。
平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动,C正确;
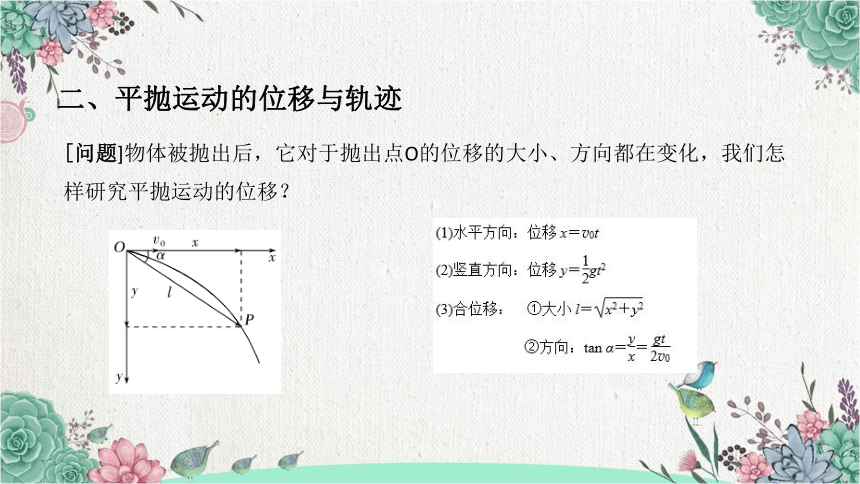
二、平抛运动的位移与轨迹
速度较小的球下降相同距离所用的时间较多
初速度:vx=v0cosθ,vy=v0sinθ。
竖直方向:只受重力作用,mg=ma
按题意作图,求得分速度后就可以求得夹角θ。
如图所示,滑板运动员以初速度v0从离地高h处的平台末端水平飞出,落在水平地面上。
[例题2]如图,某同学利用无人机玩“投弹"游戏。
初速度:vx=v0cosθ,vy=v0sinθ。
速度较大的球在相同时间间隔内下降的距离较大
空气阻力不计,则( )
如图所示,滑板运动员以初速度v0从离地高h处的平台末端水平飞出,落在水平地面上。
(1)斜抛运动和平抛运动在竖直方向上做的都是自由落体运动。
初速度:vx=v0cosθ,vy=v0sinθ。
(1)斜抛运动和平抛运动在竖直方向上做的都是自由落体运动。
按题意作图,求得分速度后就可以求得夹角θ。
(1)求小球下落的时间。
B在最高点的速度比A在最高点的大
在竖直方向只受重力,加速度为g,初速度的竖直分量为0,可以应用匀变速直线运动的规律求出竖直方向的分速度。
第五章 第四节 抛体运动的规律
一、平抛运动的速度
观察下列物体的(排球、子弹、摩托车)抛出时的速度方向。
水平方向的速度有什么特点?大小如何?竖直方向的速度有什么特点?大小如何求得?如何确定某一时刻物体的速度的大小和方向?
1.水平方向:不受力,为匀速直线运动,vx=v0。
2.竖直方向:只受重力作用,mg=ma
即a=g
所以vy=gt
下列说法是否正确:
(1)水平抛出的物体所做的运动就是平抛运动。
(2)平抛运动中要考虑空气阻力的作用。
(3)平抛运动的初速度与重力方向垂直。
(1) ×
(2) ×
(3)
√
答案:
[例题1] 将一个物体以10m/s的速度10m的高度水平抛出,落地时它的速度方向与水平地面的夹角θ是多少 不计空气阻力,g取10 m/s2。
例题分析:物体在水平方向不受力,所以加速度的水平分量0,水平方向的分速度是初速度v0=10 m/s ;在竖直方向只受重力,加速度为g,初速度的竖直分量为0,可以应用匀变速直线运动的规律求出竖直方向的分速度。
按题意作图,求得分速度后就可以求得夹角θ。
例题解答:以抛出时物体的位置O为原点,建立平面直角坐标系,x轴沿初速度方向,y轴竖直向下。
落地时,物体在水平方向的分速度vx=v0=10 m/s
根据匀变速直线运动的规律,落地时物体在竖直方向的分速度vy满足以下关系
vy2-0=2gh
由此解出
物体落地时速度与水平地面的夹角θ 是55°。
二、平抛运动的位移与轨迹
[问题]物体被抛出后,它对于抛出点O的位移的大小、方向都在变化,我们怎样研究平抛运动的位移?
[问题] 平抛运动的轨迹
下列说法是否正确:
(1)平抛运动的轨迹是抛物线,速度方向时刻变化,加速度方向也时刻变化。
(2)做平抛运动的物体质量越大,水平位移越大。
(3)从同一高度水平抛出的物体,不计空气阻力,初速度大的落地速度大。
(1)
(2) ×
(3)
×
√
答案:
[例题2]如图,某同学利用无人机玩“投弹"游戏。无人机以v0=2 m/s的速度水平向右匀速飞行,在某时刻释放了一个小球。此时无人机到水平地面的距离h =20m,空气阻力忽略不计,g取10 m/s2。
(1)求小球下落的时间。
(2)求小球释放点与落地点之间的水平距离。
分析:忽略空气阻力, 小球脱离无人机后做平抛运动,它在竖直方向的分运动是自由落体运动,根据自由落体运动的特点可以求出下落的时间,根据匀速直线运动的规律可以求出小球释放点与落地点之间的水平距离。
水平方向的速度有什么特点?大小如何?竖直方向的速度有什么特点?大小如何求得?如何确定某一时刻物体的速度的大小和方向?
二、平抛运动的位移与轨迹
(1)斜抛运动和平抛运动在竖直方向上做的都是自由落体运动。
(1)求小球下落的时间。
按题意作图,求得分速度后就可以求得夹角θ。
③轨迹对称:相对于过最高点的竖直线运动轨迹左右对称。
速度较大的球越过球网,速度较小的球没有越过球网;
(2)斜抛运动和平抛运动在水平方向上做的都是匀速直线运动。
此时无人机到水平地面的距离h =20m,空气阻力忽略不计,g取10 m/s2。
B在最高点的速度比A在最高点的大
速度较大的球越过球网,速度较小的球没有越过球网;
如图所示,滑板运动员以初速度v0从离地高h处的平台末端水平飞出,落在水平地面上。
例题分析:物体在水平方向不受力,所以加速度的水平分量0,水平方向的分速度是初速度v0=10 m/s ;
在竖直方向只受重力,加速度为g,初速度的竖直分量为0,可以应用匀变速直线运动的规律求出竖直方向的分速度。
按题意作图,求得分速度后就可以求得夹角θ。
[例题1] 将一个物体以10m/s的速度10m的高度水平抛出,落地时它的速度方向与水平地面的夹角θ是多少 不计空气阻力,g取10 m/s2。
(多选)如图所示,从地面上同一位置抛出两小球A、B,分别落在地面上的M、N点,两球运动的最大高度相同。
空气阻力不计,则( )
(2)求小球释放点与落地点之间的水平距离。
空气阻力不计,则( )
三、一般的抛体运动
观察投出去的物体(标枪、篮球) 做什么运动?
1.定义:初速度沿斜向上或斜向下方向的抛体运动。
2.初速度:vx=v0cosθ,vy=v0sinθ。
3.性质:斜抛运动可以看成是水平方向的匀速直线运动和竖直方向的竖直上抛或竖直下抛运动的合运动。
斜上抛运动的对称性
①时间对称:相对于轨迹最高点,上升时间等于下降时间。
②速度对称:相对于轨迹最高点,对称的两点速度大小相等。
③轨迹对称:相对于过最高点的竖直线运动轨迹左右对称。
下列说法是否正确:
(1)斜抛运动和平抛运动在竖直方向上做的都是自由落体运动。
(2)斜抛运动和平抛运动在水平方向上做的都是匀速直线运动。
(3)斜抛运动和平抛运动的加速度相同。
(1)
(2) √
(3) √
×
答案:
[课堂练习]
1.关于平抛运动,下面的几种说法中正确的是( )
A.平抛运动是一种不受任何外力作用的运动
B.平抛运动是曲线运动,它的速度方向不断改变,不可能是匀变速运动
C.平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动
D.平抛运动的物体质量越小,落点就越远,质量越大,落点就越近
解析 做平抛运动的物体除了受自身重力外,不受其他外力,A错误;平抛运动轨迹是抛物线,它的速度方向不断改变,物体的加速度是重力加速度,故平抛运动是匀变速曲线运动,B错误;平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动,C正确;平抛运动的运动情况与物体的质量无关,在相同高度的情况下,初速度越大,落点就越远,D错误。
答案 C
2.如图所示,滑板运动员以初速度v0从离地高h处的平台末端水平飞出,落在水平地面上。忽略空气阻力,运动员和滑板可视为质点,下列表述正确的是( )
A.v0越大,运动员在空中运动时间越长
B.v0越大,运动员落地瞬间速度越大
C.运动员落地瞬间速度与高度h无关
D.运动员落地位置与v0大小无关
3. (2017·全国卷Ⅰ,15)发球机从同一高度向正前方依次水平射出两个速度不同的乒乓球(忽略空气的影响)。速度较大的球越过球网,速度较小的球没有越过球网;其原因是( )
A.速度较小的球下降相同距离所用的时间较多
B.速度较小的球在下降相同距离时在竖直方向上的速度较大
C.速度较大的球通过同一水平距离所用的时间较少
D.速度较大的球在相同时间间隔内下降的距离较大
分析:忽略空气阻力, 小球脱离无人机后做平抛运动,它在竖直方向的分运动是自由落体运动,根据自由落体运动的特点可以求出下落的时间,根据匀速直线运动的规律可以求出小球释放点与落地点之间的水平距离。
例题分析:物体在水平方向不受力,所以加速度的水平分量0,水平方向的分速度是初速度v0=10 m/s ;
在竖直方向只受重力,加速度为g,初速度的竖直分量为0,可以应用匀变速直线运动的规律求出竖直方向的分速度。
物体落地时速度与水平地面的夹角θ 是55°。
速度较小的球在下降相同距离时在竖直方向上的速度较大
初速度:vx=v0cosθ,vy=v0sinθ。
(2)斜抛运动和平抛运动在水平方向上做的都是匀速直线运动。
关于平抛运动,下面的几种说法中正确的是( )
分析:忽略空气阻力, 小球脱离无人机后做平抛运动,它在竖直方向的分运动是自由落体运动,根据自由落体运动的特点可以求出下落的时间,根据匀速直线运动的规律可以求出小球释放点与落地点之间的水平距离。
初速度:vx=v0cosθ,vy=v0sinθ。
如图所示,滑板运动员以初速度v0从离地高h处的平台末端水平飞出,落在水平地面上。
例题分析:物体在水平方向不受力,所以加速度的水平分量0,水平方向的分速度是初速度v0=10 m/s ;
(2)斜抛运动和平抛运动在水平方向上做的都是匀速直线运动。
空气阻力不计,则( )
空气阻力不计,则( )
速度较小的球下降相同距离所用的时间较多
(2)平抛运动中要考虑空气阻力的作用。
平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动,C正确;
[问题]物体被抛出后,它对于抛出点O的位移的大小、方向都在变化,我们怎样研究平抛运动的位移?
B在最高点的速度比A在最高点的大
4.(多选)如图所示,从地面上同一位置抛出两小球A、B,分别落在地面上的M、N点,两球运动的最大高度相同。空气阻力不计,则( )
A.B的加速度比A的大
B.B的飞行时间比A的长
C.B在最高点的速度比A在最高点的大
D.B在落地时的速度比A在落地时的大
课堂小结
按题意作图,求得分速度后就可以求得夹角θ。
平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动,C正确;
二、平抛运动的位移与轨迹
速度较小的球下降相同距离所用的时间较多
初速度:vx=v0cosθ,vy=v0sinθ。
竖直方向:只受重力作用,mg=ma
按题意作图,求得分速度后就可以求得夹角θ。
如图所示,滑板运动员以初速度v0从离地高h处的平台末端水平飞出,落在水平地面上。
[例题2]如图,某同学利用无人机玩“投弹"游戏。
初速度:vx=v0cosθ,vy=v0sinθ。
速度较大的球在相同时间间隔内下降的距离较大
空气阻力不计,则( )
如图所示,滑板运动员以初速度v0从离地高h处的平台末端水平飞出,落在水平地面上。
(1)斜抛运动和平抛运动在竖直方向上做的都是自由落体运动。
初速度:vx=v0cosθ,vy=v0sinθ。
(1)斜抛运动和平抛运动在竖直方向上做的都是自由落体运动。
按题意作图,求得分速度后就可以求得夹角θ。
(1)求小球下落的时间。
B在最高点的速度比A在最高点的大
在竖直方向只受重力,加速度为g,初速度的竖直分量为0,可以应用匀变速直线运动的规律求出竖直方向的分速度。
第五章 第四节 抛体运动的规律
一、平抛运动的速度
观察下列物体的(排球、子弹、摩托车)抛出时的速度方向。
水平方向的速度有什么特点?大小如何?竖直方向的速度有什么特点?大小如何求得?如何确定某一时刻物体的速度的大小和方向?
1.水平方向:不受力,为匀速直线运动,vx=v0。
2.竖直方向:只受重力作用,mg=ma
即a=g
所以vy=gt
下列说法是否正确:
(1)水平抛出的物体所做的运动就是平抛运动。
(2)平抛运动中要考虑空气阻力的作用。
(3)平抛运动的初速度与重力方向垂直。
(1) ×
(2) ×
(3)
√
答案:
[例题1] 将一个物体以10m/s的速度10m的高度水平抛出,落地时它的速度方向与水平地面的夹角θ是多少 不计空气阻力,g取10 m/s2。
例题分析:物体在水平方向不受力,所以加速度的水平分量0,水平方向的分速度是初速度v0=10 m/s ;在竖直方向只受重力,加速度为g,初速度的竖直分量为0,可以应用匀变速直线运动的规律求出竖直方向的分速度。
按题意作图,求得分速度后就可以求得夹角θ。
例题解答:以抛出时物体的位置O为原点,建立平面直角坐标系,x轴沿初速度方向,y轴竖直向下。
落地时,物体在水平方向的分速度vx=v0=10 m/s
根据匀变速直线运动的规律,落地时物体在竖直方向的分速度vy满足以下关系
vy2-0=2gh
由此解出
物体落地时速度与水平地面的夹角θ 是55°。
二、平抛运动的位移与轨迹
[问题]物体被抛出后,它对于抛出点O的位移的大小、方向都在变化,我们怎样研究平抛运动的位移?
[问题] 平抛运动的轨迹
下列说法是否正确:
(1)平抛运动的轨迹是抛物线,速度方向时刻变化,加速度方向也时刻变化。
(2)做平抛运动的物体质量越大,水平位移越大。
(3)从同一高度水平抛出的物体,不计空气阻力,初速度大的落地速度大。
(1)
(2) ×
(3)
×
√
答案:
[例题2]如图,某同学利用无人机玩“投弹"游戏。无人机以v0=2 m/s的速度水平向右匀速飞行,在某时刻释放了一个小球。此时无人机到水平地面的距离h =20m,空气阻力忽略不计,g取10 m/s2。
(1)求小球下落的时间。
(2)求小球释放点与落地点之间的水平距离。
分析:忽略空气阻力, 小球脱离无人机后做平抛运动,它在竖直方向的分运动是自由落体运动,根据自由落体运动的特点可以求出下落的时间,根据匀速直线运动的规律可以求出小球释放点与落地点之间的水平距离。
水平方向的速度有什么特点?大小如何?竖直方向的速度有什么特点?大小如何求得?如何确定某一时刻物体的速度的大小和方向?
二、平抛运动的位移与轨迹
(1)斜抛运动和平抛运动在竖直方向上做的都是自由落体运动。
(1)求小球下落的时间。
按题意作图,求得分速度后就可以求得夹角θ。
③轨迹对称:相对于过最高点的竖直线运动轨迹左右对称。
速度较大的球越过球网,速度较小的球没有越过球网;
(2)斜抛运动和平抛运动在水平方向上做的都是匀速直线运动。
此时无人机到水平地面的距离h =20m,空气阻力忽略不计,g取10 m/s2。
B在最高点的速度比A在最高点的大
速度较大的球越过球网,速度较小的球没有越过球网;
如图所示,滑板运动员以初速度v0从离地高h处的平台末端水平飞出,落在水平地面上。
例题分析:物体在水平方向不受力,所以加速度的水平分量0,水平方向的分速度是初速度v0=10 m/s ;
在竖直方向只受重力,加速度为g,初速度的竖直分量为0,可以应用匀变速直线运动的规律求出竖直方向的分速度。
按题意作图,求得分速度后就可以求得夹角θ。
[例题1] 将一个物体以10m/s的速度10m的高度水平抛出,落地时它的速度方向与水平地面的夹角θ是多少 不计空气阻力,g取10 m/s2。
(多选)如图所示,从地面上同一位置抛出两小球A、B,分别落在地面上的M、N点,两球运动的最大高度相同。
空气阻力不计,则( )
(2)求小球释放点与落地点之间的水平距离。
空气阻力不计,则( )
三、一般的抛体运动
观察投出去的物体(标枪、篮球) 做什么运动?
1.定义:初速度沿斜向上或斜向下方向的抛体运动。
2.初速度:vx=v0cosθ,vy=v0sinθ。
3.性质:斜抛运动可以看成是水平方向的匀速直线运动和竖直方向的竖直上抛或竖直下抛运动的合运动。
斜上抛运动的对称性
①时间对称:相对于轨迹最高点,上升时间等于下降时间。
②速度对称:相对于轨迹最高点,对称的两点速度大小相等。
③轨迹对称:相对于过最高点的竖直线运动轨迹左右对称。
下列说法是否正确:
(1)斜抛运动和平抛运动在竖直方向上做的都是自由落体运动。
(2)斜抛运动和平抛运动在水平方向上做的都是匀速直线运动。
(3)斜抛运动和平抛运动的加速度相同。
(1)
(2) √
(3) √
×
答案:
[课堂练习]
1.关于平抛运动,下面的几种说法中正确的是( )
A.平抛运动是一种不受任何外力作用的运动
B.平抛运动是曲线运动,它的速度方向不断改变,不可能是匀变速运动
C.平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动
D.平抛运动的物体质量越小,落点就越远,质量越大,落点就越近
解析 做平抛运动的物体除了受自身重力外,不受其他外力,A错误;平抛运动轨迹是抛物线,它的速度方向不断改变,物体的加速度是重力加速度,故平抛运动是匀变速曲线运动,B错误;平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动,C正确;平抛运动的运动情况与物体的质量无关,在相同高度的情况下,初速度越大,落点就越远,D错误。
答案 C
2.如图所示,滑板运动员以初速度v0从离地高h处的平台末端水平飞出,落在水平地面上。忽略空气阻力,运动员和滑板可视为质点,下列表述正确的是( )
A.v0越大,运动员在空中运动时间越长
B.v0越大,运动员落地瞬间速度越大
C.运动员落地瞬间速度与高度h无关
D.运动员落地位置与v0大小无关
3. (2017·全国卷Ⅰ,15)发球机从同一高度向正前方依次水平射出两个速度不同的乒乓球(忽略空气的影响)。速度较大的球越过球网,速度较小的球没有越过球网;其原因是( )
A.速度较小的球下降相同距离所用的时间较多
B.速度较小的球在下降相同距离时在竖直方向上的速度较大
C.速度较大的球通过同一水平距离所用的时间较少
D.速度较大的球在相同时间间隔内下降的距离较大
分析:忽略空气阻力, 小球脱离无人机后做平抛运动,它在竖直方向的分运动是自由落体运动,根据自由落体运动的特点可以求出下落的时间,根据匀速直线运动的规律可以求出小球释放点与落地点之间的水平距离。
例题分析:物体在水平方向不受力,所以加速度的水平分量0,水平方向的分速度是初速度v0=10 m/s ;
在竖直方向只受重力,加速度为g,初速度的竖直分量为0,可以应用匀变速直线运动的规律求出竖直方向的分速度。
物体落地时速度与水平地面的夹角θ 是55°。
速度较小的球在下降相同距离时在竖直方向上的速度较大
初速度:vx=v0cosθ,vy=v0sinθ。
(2)斜抛运动和平抛运动在水平方向上做的都是匀速直线运动。
关于平抛运动,下面的几种说法中正确的是( )
分析:忽略空气阻力, 小球脱离无人机后做平抛运动,它在竖直方向的分运动是自由落体运动,根据自由落体运动的特点可以求出下落的时间,根据匀速直线运动的规律可以求出小球释放点与落地点之间的水平距离。
初速度:vx=v0cosθ,vy=v0sinθ。
如图所示,滑板运动员以初速度v0从离地高h处的平台末端水平飞出,落在水平地面上。
例题分析:物体在水平方向不受力,所以加速度的水平分量0,水平方向的分速度是初速度v0=10 m/s ;
(2)斜抛运动和平抛运动在水平方向上做的都是匀速直线运动。
空气阻力不计,则( )
空气阻力不计,则( )
速度较小的球下降相同距离所用的时间较多
(2)平抛运动中要考虑空气阻力的作用。
平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动,C正确;
[问题]物体被抛出后,它对于抛出点O的位移的大小、方向都在变化,我们怎样研究平抛运动的位移?
B在最高点的速度比A在最高点的大
4.(多选)如图所示,从地面上同一位置抛出两小球A、B,分别落在地面上的M、N点,两球运动的最大高度相同。空气阻力不计,则( )
A.B的加速度比A的大
B.B的飞行时间比A的长
C.B在最高点的速度比A在最高点的大
D.B在落地时的速度比A在落地时的大
课堂小结
