7.2 定义与命题第2课时(同步课件)-2023-2024学年八年级数学上册同步精品课堂(北师大版)
文档属性
| 名称 | 7.2 定义与命题第2课时(同步课件)-2023-2024学年八年级数学上册同步精品课堂(北师大版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-23 09:24:01 | ||
图片预览








文档简介
(共23张PPT)
北师大版 数学 八年级上册
第2课时
第七章 平行线的证明
2 定义与命题
学习目标
1.了解公理、定理与证明的概念并了解本套教材所采用的公理.(重点)
2.体会命题证明的必要性,体验数学思维的严谨性.(难点)
复习回顾
1.对名称和术语的含义加以描述,作出明确规定.也就是给出它们的 .
定义
2.判断一件事情的句子,叫做 .一般地,每个命题都由 和 两部分组成. 是已知的事项, 是由已知事项推断出的事项.
命题
条件
结论
条件
结论
3.命题通常可以写成 的形式,其中, 引出的部分是条件, 引出的部分是结论.
“如果……那么…….”
“如果”
“那么”
4. 的命题称为真命题, 的命题称为假命题.一个例子具备命题的条件,而不具有命题的结论,这种例子称为 .
正确
不正确
反例
一、创设情境,引入新知
用我们以前学过的观察,实验,验证特例等方法.
能不能根据已经知道的真命题证实呢
这些方法往往不可靠.
哦……那可怎么办
那已经知道的真命题又是如何证实的
想一想:举一个反例就可以说明一个命题是假命题,那么如何证实一个命题是真命题呢?
一、创设情境,引入新知
要说明一个命题是正确的,无论验证多少个特例,也无法保证命题的正确性.如何验证命题的正确性,其实在数学发展史上,数学家们也遇到过类似的问题.
公元前3世纪,人们已经积累了大量的数学知识,在此基础上,古希腊数学家欧几里得编写了一本书,书名叫做《原本》.为了说明每一结论的正确性,他在编写这本书时进行了大胆的创造……
二、自主合作,探究新知
探究:公理与定理
欧几里得挑选了一部分数学名词和一部分公认的真命题作为证实其它命题的出发点和依据.
1.原名:其中的数学名词称为原名.
2.公理:公认的真命题称为公理.
3.证明:除了公理外,其他真命题的真假都需要通过演绎推理的方法进行判断.演绎推理的过程称为证明.
4.定理:经过证明的真命题称为定理.
每个定理都只能用公理、定义和已经证明为真的命题来证明.
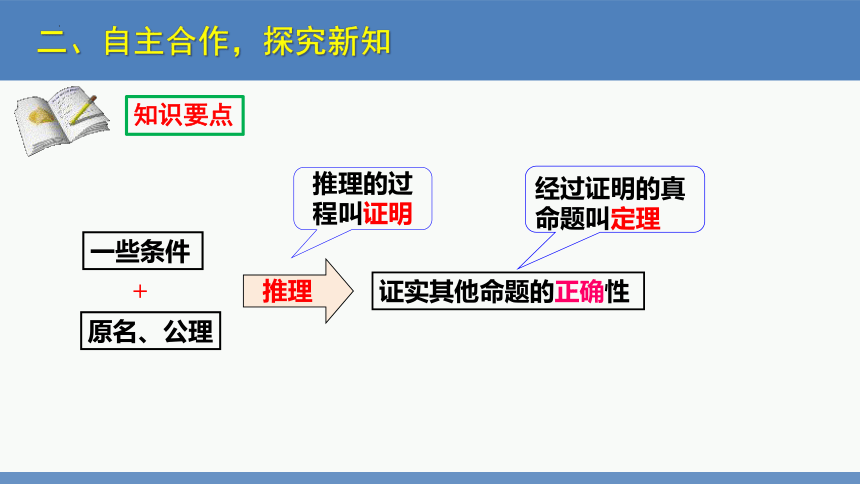
二、自主合作,探究新知
证实其他命题的正确性
推理
推理的过程叫证明
经过证明的真命题叫定理
原名、公理
一些条件
+
知识要点
二、自主合作,探究新知
典型例题
例1:下列叙述错误的是( )
A.所有的命题都有条件和结论
B.所有的命题都是定理
C.所有的定理都是命题
D.所有的公理都是真命题
B
二、自主合作,探究新知
本套教科书选用九条基本事实作为证明的出发点和依据,我们已经认识了其中的八条,它们是:
1.两点确定一条直线;
2.两点之间线段最短;
3.同一平面内,过一点有且只有一条直线与已知直线垂直;
4.两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行(简述为:同位角相等,两直线平行);
5.过直线外一点有且只有一条直线与这条直线平行;
6.两边及其夹角分别相等的两个三角形全等;
7.两角及其夹边分别相等的两个三角形全等;
8.三边分别相等的两个三角形全等.
这些基本事实又叫做公理
二、自主合作,探究新知
此外,数与式的运算律和运算法则、等式的有关性质以及反映大小关系的有关性质都可以作为证明的依据.
例如,如果a=b,b=c,那么a=c,这一性质也可以作为证明的依据,称为“等量代换”.又如,如果a>b,b>c,那么a>c,这一性质同样也可以作为证明的依据.
另外一条基本事实我们将在后面的学习中认识它.
二、自主合作,探究新知
从这些基本事实出发,就可以证明已经探索过的结论了.例如,我们可以证明下面的定理:
定理:同角(等角)的补角相等.
定理:同角(等角)的余角相等.
定理:三角形的任意两边之和大于第三边.
二、自主合作,探究新知
典型例题
由上面的例题,我们可以得到定理:对顶角相等.
∴ ∠AOB与∠COD都是平角( )
平角的定义
∴ ∠AOC =∠BOD ( )
同角的补角相等
∠BOD+∠AOD=180°( )
补角的定义
∴ ∠AOC+∠AOD=180°
例2:已知:如图,直线AB与直线CD相交于点O,
∠AOC与∠BOD是对顶角.
求证:∠AOC =∠BOD.
证明:
∵直线AB与直线CD相交于点O ( )
已知
二、自主合作,探究新知
证明定理的一般步骤:
(1)根据条件,画出图形,并在图形上标出有关字母与符号;
(2)结合图形,写出已知、求证;
(3)分析因果关系,找出由已知推出结论的途径;
(4)有条理地写出证明过程(每一步推理要有依据).
知识要点
例3:已知:b∥c, a⊥b .
求证:a⊥c.
a
b
c
1
2
二、自主合作,探究新知
证明: ∵ a ⊥b(已知)
∴ ∠1=90°(垂直的定义)
又∴ b ∥ c(已知)
∴ ∠2=∠1=90°(两直线平行,同位角相等)
∴ a ⊥ c(垂直的定义).
典型例题
三、即学即练,应用知识
2. 命题、定理、公理的关系如下:①公理是真命题;②定理是由基本定义和公理推出来的真命题;③真命题是公理;④真命题一定是定理.其中正确的有( )
A.1个 B.2个 C.3 个 D.4个
1.下列语句中属于定理的是( )
A 在直线 AB 上任取一点 E
B.如果两个角相等,那么这两个角是对顶角
C.∠A> ∠B
D.到一条线段两个端点的距离相等的点,在这条线段的垂直平分线上
D
B
三、即学即练,应用知识
3.下列推理证明中,错误的是( )
A.∵AB = CD,CD = EF,∴ AB = EF
B.∵∠α=∠β,∠β=∠γ,∴∠α=∠γ
C.∵ a // b,b //c, ∴a // c
D.∵AB⊥EF,EF⊥CD,∴AB⊥CD
D
4.已知a,b,c 为平面内三条不同的直线,若a⊥b,c⊥b.则a与c 的位置关系是
.
平行
三、即学即练,应用知识
5.求证:直角三角形的两个锐角互余.
已知:如图所示,在△ABC中,∠C=90°.
求证:∠A与∠B互余.
证明:∵ ∠A+∠B+∠C=180°(三角形内角和等于180°),
又∵∠C=90°,
∴ ∠A+∠B=180°-∠C=90°.
∴ ∠A与∠B互余.
三、即学即练,应用知识
6.如图所示,在直线AC上取一点O,作射线OB,OE和OF分别平分∠AOB和∠BOC.
求证:OE⊥OF.
证明:∵ OE和OF分别平分∠AOB和∠BOC,
∴ ∠EOB=∠AOB,∠BOF=∠BOC.
又∵ ∠AOB+∠BOC=180°,
∴ ∠EOB+∠BOF= (∠AOB+∠BOC)=×180°=90°,
即∠EOF=90°,
∴ OE⊥OF.
四、课堂小结
定义与命题2
证明:推理的过程
公理:公认的真命题
定理:经过证明的真命题
分类
五、当堂达标检测
1.“两点之间,线段最短”这个语句是( )
A.定理 B.公理 C.定义 D.只是命题
B
2.下列说法正确的是( )
A.命题一定是正确的
B.不正确的判断就不是命题
C.定理都是真命题
D.真命题都是定理
C
3.∠AOB与∠BOC互为补角,OD 平分∠AOB,∠2+∠3=90°,如图所示.
求证:∠BOE =∠BOC.请完成下列证明.
证明:∵∠AOB 与∠BOC互为补角(已知),
∴∠AOB+ ∠BOC = (补角的定义),
即∠1+ ∠2+ ∠3+∠4= .
又∵∠2+ ∠3=90°(已知),
∴∠1+∠4= (等式的性质),
即∠1与∠4互余,∠2与∠3互余( ),
∵ OD平分∠AOB,∴∠1 =∠2( ),
∴∠3=∠4( ),
即∠BOE ==∠BOC.
C
E
O
A
B
D
1
2
3
4
五、当堂达标检测
180°
180°
90°
余角的定义
角平分线的性质
余角的性质
4.如图,若∠1=∠2,则∠3=∠4 ,请用推理的方法说明它是真命题。
1
3
4
a
b
2
五、当堂达标检测
解:∵∠1=∠2 (已),
∴∠3=∠4
(两直线平行,内错角相等)
∴a∥b
(同位角相等,两直线平行)
教材习题7.3.
六、布置作业
北师大版 数学 八年级上册
第2课时
第七章 平行线的证明
2 定义与命题
学习目标
1.了解公理、定理与证明的概念并了解本套教材所采用的公理.(重点)
2.体会命题证明的必要性,体验数学思维的严谨性.(难点)
复习回顾
1.对名称和术语的含义加以描述,作出明确规定.也就是给出它们的 .
定义
2.判断一件事情的句子,叫做 .一般地,每个命题都由 和 两部分组成. 是已知的事项, 是由已知事项推断出的事项.
命题
条件
结论
条件
结论
3.命题通常可以写成 的形式,其中, 引出的部分是条件, 引出的部分是结论.
“如果……那么…….”
“如果”
“那么”
4. 的命题称为真命题, 的命题称为假命题.一个例子具备命题的条件,而不具有命题的结论,这种例子称为 .
正确
不正确
反例
一、创设情境,引入新知
用我们以前学过的观察,实验,验证特例等方法.
能不能根据已经知道的真命题证实呢
这些方法往往不可靠.
哦……那可怎么办
那已经知道的真命题又是如何证实的
想一想:举一个反例就可以说明一个命题是假命题,那么如何证实一个命题是真命题呢?
一、创设情境,引入新知
要说明一个命题是正确的,无论验证多少个特例,也无法保证命题的正确性.如何验证命题的正确性,其实在数学发展史上,数学家们也遇到过类似的问题.
公元前3世纪,人们已经积累了大量的数学知识,在此基础上,古希腊数学家欧几里得编写了一本书,书名叫做《原本》.为了说明每一结论的正确性,他在编写这本书时进行了大胆的创造……
二、自主合作,探究新知
探究:公理与定理
欧几里得挑选了一部分数学名词和一部分公认的真命题作为证实其它命题的出发点和依据.
1.原名:其中的数学名词称为原名.
2.公理:公认的真命题称为公理.
3.证明:除了公理外,其他真命题的真假都需要通过演绎推理的方法进行判断.演绎推理的过程称为证明.
4.定理:经过证明的真命题称为定理.
每个定理都只能用公理、定义和已经证明为真的命题来证明.
二、自主合作,探究新知
证实其他命题的正确性
推理
推理的过程叫证明
经过证明的真命题叫定理
原名、公理
一些条件
+
知识要点
二、自主合作,探究新知
典型例题
例1:下列叙述错误的是( )
A.所有的命题都有条件和结论
B.所有的命题都是定理
C.所有的定理都是命题
D.所有的公理都是真命题
B
二、自主合作,探究新知
本套教科书选用九条基本事实作为证明的出发点和依据,我们已经认识了其中的八条,它们是:
1.两点确定一条直线;
2.两点之间线段最短;
3.同一平面内,过一点有且只有一条直线与已知直线垂直;
4.两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行(简述为:同位角相等,两直线平行);
5.过直线外一点有且只有一条直线与这条直线平行;
6.两边及其夹角分别相等的两个三角形全等;
7.两角及其夹边分别相等的两个三角形全等;
8.三边分别相等的两个三角形全等.
这些基本事实又叫做公理
二、自主合作,探究新知
此外,数与式的运算律和运算法则、等式的有关性质以及反映大小关系的有关性质都可以作为证明的依据.
例如,如果a=b,b=c,那么a=c,这一性质也可以作为证明的依据,称为“等量代换”.又如,如果a>b,b>c,那么a>c,这一性质同样也可以作为证明的依据.
另外一条基本事实我们将在后面的学习中认识它.
二、自主合作,探究新知
从这些基本事实出发,就可以证明已经探索过的结论了.例如,我们可以证明下面的定理:
定理:同角(等角)的补角相等.
定理:同角(等角)的余角相等.
定理:三角形的任意两边之和大于第三边.
二、自主合作,探究新知
典型例题
由上面的例题,我们可以得到定理:对顶角相等.
∴ ∠AOB与∠COD都是平角( )
平角的定义
∴ ∠AOC =∠BOD ( )
同角的补角相等
∠BOD+∠AOD=180°( )
补角的定义
∴ ∠AOC+∠AOD=180°
例2:已知:如图,直线AB与直线CD相交于点O,
∠AOC与∠BOD是对顶角.
求证:∠AOC =∠BOD.
证明:
∵直线AB与直线CD相交于点O ( )
已知
二、自主合作,探究新知
证明定理的一般步骤:
(1)根据条件,画出图形,并在图形上标出有关字母与符号;
(2)结合图形,写出已知、求证;
(3)分析因果关系,找出由已知推出结论的途径;
(4)有条理地写出证明过程(每一步推理要有依据).
知识要点
例3:已知:b∥c, a⊥b .
求证:a⊥c.
a
b
c
1
2
二、自主合作,探究新知
证明: ∵ a ⊥b(已知)
∴ ∠1=90°(垂直的定义)
又∴ b ∥ c(已知)
∴ ∠2=∠1=90°(两直线平行,同位角相等)
∴ a ⊥ c(垂直的定义).
典型例题
三、即学即练,应用知识
2. 命题、定理、公理的关系如下:①公理是真命题;②定理是由基本定义和公理推出来的真命题;③真命题是公理;④真命题一定是定理.其中正确的有( )
A.1个 B.2个 C.3 个 D.4个
1.下列语句中属于定理的是( )
A 在直线 AB 上任取一点 E
B.如果两个角相等,那么这两个角是对顶角
C.∠A> ∠B
D.到一条线段两个端点的距离相等的点,在这条线段的垂直平分线上
D
B
三、即学即练,应用知识
3.下列推理证明中,错误的是( )
A.∵AB = CD,CD = EF,∴ AB = EF
B.∵∠α=∠β,∠β=∠γ,∴∠α=∠γ
C.∵ a // b,b //c, ∴a // c
D.∵AB⊥EF,EF⊥CD,∴AB⊥CD
D
4.已知a,b,c 为平面内三条不同的直线,若a⊥b,c⊥b.则a与c 的位置关系是
.
平行
三、即学即练,应用知识
5.求证:直角三角形的两个锐角互余.
已知:如图所示,在△ABC中,∠C=90°.
求证:∠A与∠B互余.
证明:∵ ∠A+∠B+∠C=180°(三角形内角和等于180°),
又∵∠C=90°,
∴ ∠A+∠B=180°-∠C=90°.
∴ ∠A与∠B互余.
三、即学即练,应用知识
6.如图所示,在直线AC上取一点O,作射线OB,OE和OF分别平分∠AOB和∠BOC.
求证:OE⊥OF.
证明:∵ OE和OF分别平分∠AOB和∠BOC,
∴ ∠EOB=∠AOB,∠BOF=∠BOC.
又∵ ∠AOB+∠BOC=180°,
∴ ∠EOB+∠BOF= (∠AOB+∠BOC)=×180°=90°,
即∠EOF=90°,
∴ OE⊥OF.
四、课堂小结
定义与命题2
证明:推理的过程
公理:公认的真命题
定理:经过证明的真命题
分类
五、当堂达标检测
1.“两点之间,线段最短”这个语句是( )
A.定理 B.公理 C.定义 D.只是命题
B
2.下列说法正确的是( )
A.命题一定是正确的
B.不正确的判断就不是命题
C.定理都是真命题
D.真命题都是定理
C
3.∠AOB与∠BOC互为补角,OD 平分∠AOB,∠2+∠3=90°,如图所示.
求证:∠BOE =∠BOC.请完成下列证明.
证明:∵∠AOB 与∠BOC互为补角(已知),
∴∠AOB+ ∠BOC = (补角的定义),
即∠1+ ∠2+ ∠3+∠4= .
又∵∠2+ ∠3=90°(已知),
∴∠1+∠4= (等式的性质),
即∠1与∠4互余,∠2与∠3互余( ),
∵ OD平分∠AOB,∴∠1 =∠2( ),
∴∠3=∠4( ),
即∠BOE ==∠BOC.
C
E
O
A
B
D
1
2
3
4
五、当堂达标检测
180°
180°
90°
余角的定义
角平分线的性质
余角的性质
4.如图,若∠1=∠2,则∠3=∠4 ,请用推理的方法说明它是真命题。
1
3
4
a
b
2
五、当堂达标检测
解:∵∠1=∠2 (已),
∴∠3=∠4
(两直线平行,内错角相等)
∴a∥b
(同位角相等,两直线平行)
教材习题7.3.
六、布置作业
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
