15.2 线段的垂直平分线 课件(共22张PPT) 沪科版八年级上册数学
文档属性
| 名称 | 15.2 线段的垂直平分线 课件(共22张PPT) 沪科版八年级上册数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 223.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-21 10:29:00 | ||
图片预览




文档简介
(共22张PPT)
第十五章 轴对称图形与等腰三角形
15.2 线段的垂直平分线
1.能够利用尺规作图作一条已知线段的垂直平分线,并能证明它的正确性;
2.理解线段的垂直平分线的性质定理及其逆定理;
3.知道三角形三边的垂直平分线的交点的性质.
一、学习目标
二、新课导入
如图,A、B、C三个村庄合建一所学校,要求校址P点距离三个村庄都相等.请你帮助确定校址.
A
B
C
·
·
·
三、概念剖析
怎样作出线段的垂直平分线?有哪几种作法?
方法一:用刻度尺量出线段的中点,再用三角尺过中点画垂线的方法作出线段的垂直平分线.
(一)线段垂直平分线的画法
A
B
O
三、概念剖析
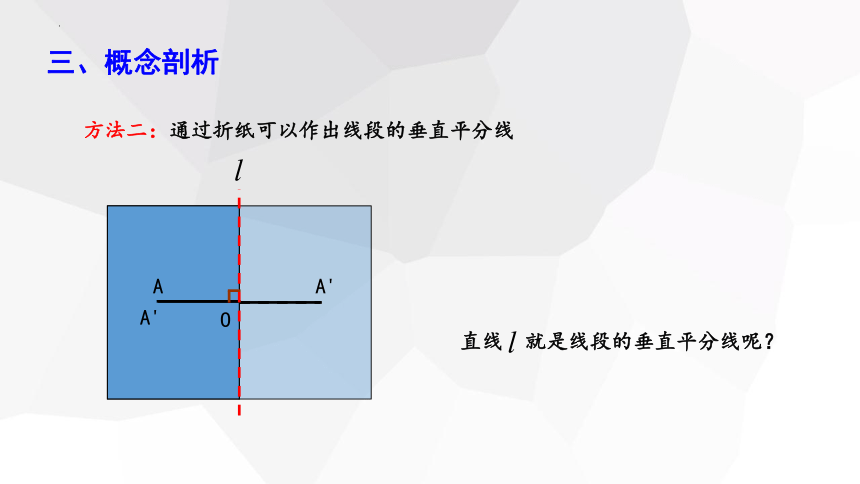
方法二:通过折纸可以作出线段的垂直平分线
A
A'
(A’)
O
O
A
A'
直线 就是线段的垂直平分线呢?
三、概念剖析
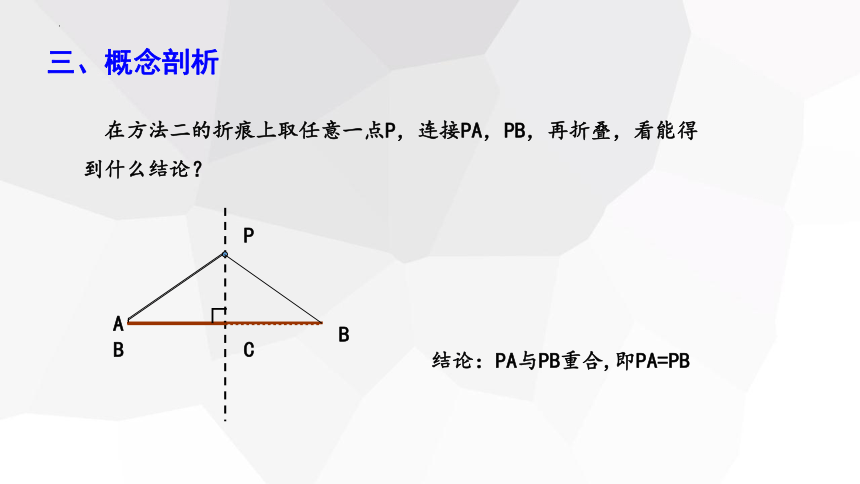
在方法二的折痕上取任意一点P,连接PA,PB,再折叠,看能得到什么结论?
结论:PA与PB重合,即PA=PB
A
B
P
C
B
三、概念剖析
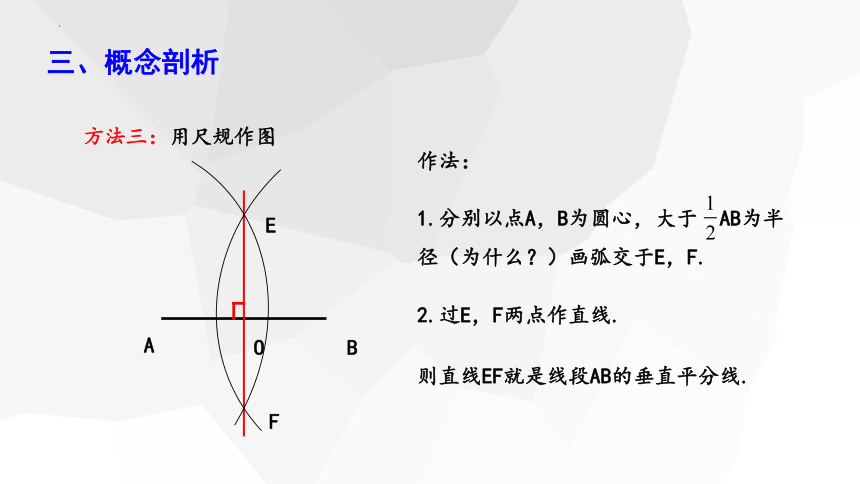
方法三:用尺规作图
A
B
E
F
O
作法:
2.过E,F两点作直线.
则直线EF就是线段AB的垂直平分线.
1.分别以点A,B为圆心,大于 AB为半径(为什么?)画弧交于E,F.
三、概念剖析
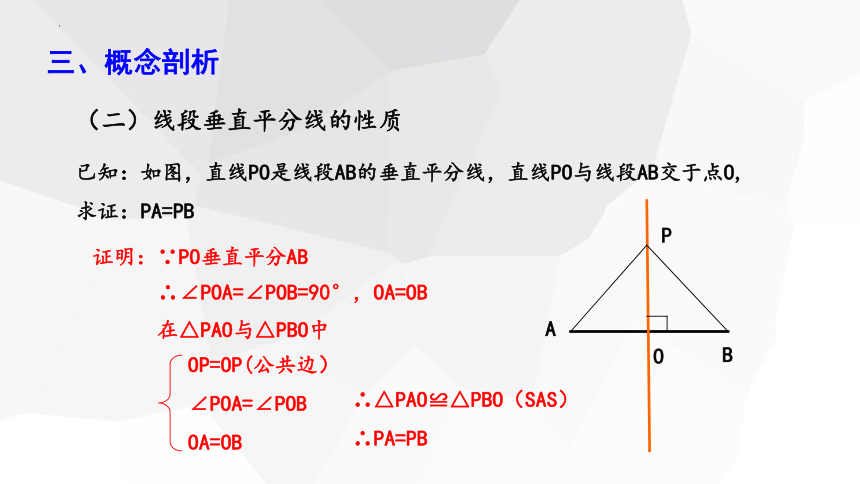
(二)线段垂直平分线的性质
已知:如图,直线PO是线段AB的垂直平分线,直线PO与线段AB交于点O,
求证:PA=PB
A
B
P
O
证明:∵PO垂直平分AB
∴∠POA=∠POB=90°,OA=OB
在△PAO与△PBO中
OP=OP(公共边)
∠POA=∠POB
OA=OB
∴△PAO≌△PBO(SAS)
∴PA=PB
三、概念剖析
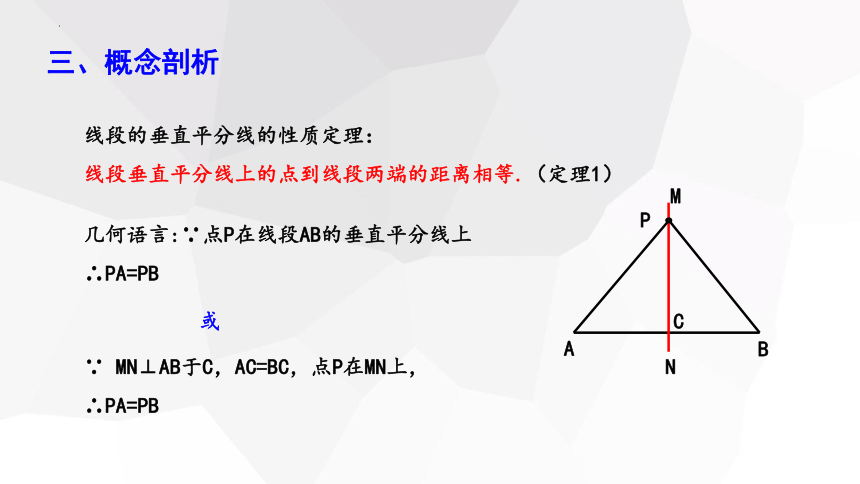
线段的垂直平分线的性质定理:
线段垂直平分线上的点到线段两端的距离相等.(定理1)
几何语言:∵点P在线段AB的垂直平分线上
∴PA=PB
∵ MN⊥AB于C,AC=BC,点P在MN上,
∴PA=PB
N
A
B
P
M
或
C
三、概念剖析
线段的垂直平分线上的点到线段两个端点的距离相等.
到一条线段的两个端点距离相等的点,在这条线段的垂直平分线上.(定理2)
逆命题
例1:如图,已知点A、点B以及直线l.
(1)用尺规作图的方法在直线l上求作一点P,使PA=PB.(保留作图痕迹,不要求写出作法);
(2)在(1)中所作的图中,若AM=PN,BN=PM,求证:∠MAP=∠NPB.
分析:(1)用尺规作图画出线段AB的垂直平分线.
(2)利用全等三角形的判定方法以及利用其性质即可证明.
M
N
A
B
l
四、典型例题
四、典型例题
M
N
A
B
l
P
解:(1)如图所示:
(1)用尺规作图的方法在直线l上求作一点P,使PA=PB.(保留作图痕迹,不要求写出作法);
(2)在(1)中所作的图中,若AM=PN,BN=PM,求证:∠MAP=∠NPB.
解:(2)在△AMP和△BNP中,
∵AM=PN,AP=BP,PM=BN,
∴△AMP≌△PNB(SSS),
∴∠MAP=∠NPB.
四、典型例题
M
N
A
B
l
P
归纳:
用尺规作线段AB的垂直平分线的步骤:
四、典型例题
2.过E,F两点作直线.
则直线EF就是线段AB的垂直平分线.
1.分别以点A,B为圆心,大于 AB为半径,画弧交于E,F.
A
B
E
F
O
线段垂直平分线上的点到线段两端的距离相等.
1.如图,A、B、C三个村庄合建一所学校,要求校址P点距离三个村庄都相等.请你帮助确定校址.
点P为校址.
A
B
C
·
·
·
P
·
解:如图:
【当堂检测】
【当堂检测】
2.如图所示,直线CD是线段AB的垂直平分线,点P为直线CD上的一点,且PA=5,则线段PB的长为 .
5
解:∵直线CD是线段AB的垂直平分线,P为直线CD上的一点,
∴PB=PA=5.
P
A
B
C
D
【当堂检测】
解:∵△DBC的周长为BC+BD+CD=35cm,
又∵DE垂直平分AB,
∴AD=BD,故BC+AD+CD=35cm.
∵AC=AD+DC=20cm,
∴BC=35-20=15(cm).
3.如图,在△ABC中,AB=AC=20cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为35cm,求BC的长.
方法归纳:利用线段垂直平分线的性质,实现线段之间的相互转化,从而求出未知线段的长.
例2:已知:如图△ABC中,边AB、BC的垂直平分线相交于点P.
求证:PA=PB=PC.
∴PA=PB=PC.
A
C
B
M
P
N
M'
N'
证明: ∵点P在线段AB的垂直平分线上,点P在线段BC的垂直平分线上(已知)
∴PA=PB ,PB=PC(线段垂直平分线上的点到线段两端的距离相等)
四、典型例题
总结:在△ABC中,若AB、BC的垂直平分线相交于点P,则点P也在AC的垂直平分线上.
归纳:
四、典型例题
三角形三边的垂直平分线相交于一点,这点到三角形三个顶点的距离相等.
线段垂直平分线的判定:
到线段两端距离相等的点在线段的垂直平分线上.
作用:判断一个点是否在线段的垂直平分线上.
D
【当堂检测】
4.如图,在△ABC中,分别以点A,B为圆心,大于 AB长为半径画弧,两弧分别交于点D,E,则直线DE是( )
A. ∠A的平分线 B. AC边的中线
C. BC边的高线 D. AB边的垂直平分线
解:分别以点A,B为圆心,大于 AB长为半径画弧,两弧分别交于点D,E.
∴DA=DB,EA=EB,
∴点D,E在线段AB的垂直平分线上.
【当堂检测】
5.已知:如图,点C,D是线段AB外的两点,且AC=BC,AD=BD,AB与CD相交于点O.求证:AO=BO.
证明:∵AC=BC,AD=BD,
∴点C和点D在线段AB的垂直平分线上,
∴CD为线段AB的垂直平分线.
又∵AB与CD相交于点O,
∴AO=BO.
五、课堂总结
画法:尺规作图
线段的垂直平分线
定理1:线段的垂直平分线上的点到线段的两端的距离相等;
定理2:到线段的两端距离相等的点在线段的垂直平分线上.
第十五章 轴对称图形与等腰三角形
15.2 线段的垂直平分线
1.能够利用尺规作图作一条已知线段的垂直平分线,并能证明它的正确性;
2.理解线段的垂直平分线的性质定理及其逆定理;
3.知道三角形三边的垂直平分线的交点的性质.
一、学习目标
二、新课导入
如图,A、B、C三个村庄合建一所学校,要求校址P点距离三个村庄都相等.请你帮助确定校址.
A
B
C
·
·
·
三、概念剖析
怎样作出线段的垂直平分线?有哪几种作法?
方法一:用刻度尺量出线段的中点,再用三角尺过中点画垂线的方法作出线段的垂直平分线.
(一)线段垂直平分线的画法
A
B
O
三、概念剖析
方法二:通过折纸可以作出线段的垂直平分线
A
A'
(A’)
O
O
A
A'
直线 就是线段的垂直平分线呢?
三、概念剖析
在方法二的折痕上取任意一点P,连接PA,PB,再折叠,看能得到什么结论?
结论:PA与PB重合,即PA=PB
A
B
P
C
B
三、概念剖析
方法三:用尺规作图
A
B
E
F
O
作法:
2.过E,F两点作直线.
则直线EF就是线段AB的垂直平分线.
1.分别以点A,B为圆心,大于 AB为半径(为什么?)画弧交于E,F.
三、概念剖析
(二)线段垂直平分线的性质
已知:如图,直线PO是线段AB的垂直平分线,直线PO与线段AB交于点O,
求证:PA=PB
A
B
P
O
证明:∵PO垂直平分AB
∴∠POA=∠POB=90°,OA=OB
在△PAO与△PBO中
OP=OP(公共边)
∠POA=∠POB
OA=OB
∴△PAO≌△PBO(SAS)
∴PA=PB
三、概念剖析
线段的垂直平分线的性质定理:
线段垂直平分线上的点到线段两端的距离相等.(定理1)
几何语言:∵点P在线段AB的垂直平分线上
∴PA=PB
∵ MN⊥AB于C,AC=BC,点P在MN上,
∴PA=PB
N
A
B
P
M
或
C
三、概念剖析
线段的垂直平分线上的点到线段两个端点的距离相等.
到一条线段的两个端点距离相等的点,在这条线段的垂直平分线上.(定理2)
逆命题
例1:如图,已知点A、点B以及直线l.
(1)用尺规作图的方法在直线l上求作一点P,使PA=PB.(保留作图痕迹,不要求写出作法);
(2)在(1)中所作的图中,若AM=PN,BN=PM,求证:∠MAP=∠NPB.
分析:(1)用尺规作图画出线段AB的垂直平分线.
(2)利用全等三角形的判定方法以及利用其性质即可证明.
M
N
A
B
l
四、典型例题
四、典型例题
M
N
A
B
l
P
解:(1)如图所示:
(1)用尺规作图的方法在直线l上求作一点P,使PA=PB.(保留作图痕迹,不要求写出作法);
(2)在(1)中所作的图中,若AM=PN,BN=PM,求证:∠MAP=∠NPB.
解:(2)在△AMP和△BNP中,
∵AM=PN,AP=BP,PM=BN,
∴△AMP≌△PNB(SSS),
∴∠MAP=∠NPB.
四、典型例题
M
N
A
B
l
P
归纳:
用尺规作线段AB的垂直平分线的步骤:
四、典型例题
2.过E,F两点作直线.
则直线EF就是线段AB的垂直平分线.
1.分别以点A,B为圆心,大于 AB为半径,画弧交于E,F.
A
B
E
F
O
线段垂直平分线上的点到线段两端的距离相等.
1.如图,A、B、C三个村庄合建一所学校,要求校址P点距离三个村庄都相等.请你帮助确定校址.
点P为校址.
A
B
C
·
·
·
P
·
解:如图:
【当堂检测】
【当堂检测】
2.如图所示,直线CD是线段AB的垂直平分线,点P为直线CD上的一点,且PA=5,则线段PB的长为 .
5
解:∵直线CD是线段AB的垂直平分线,P为直线CD上的一点,
∴PB=PA=5.
P
A
B
C
D
【当堂检测】
解:∵△DBC的周长为BC+BD+CD=35cm,
又∵DE垂直平分AB,
∴AD=BD,故BC+AD+CD=35cm.
∵AC=AD+DC=20cm,
∴BC=35-20=15(cm).
3.如图,在△ABC中,AB=AC=20cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为35cm,求BC的长.
方法归纳:利用线段垂直平分线的性质,实现线段之间的相互转化,从而求出未知线段的长.
例2:已知:如图△ABC中,边AB、BC的垂直平分线相交于点P.
求证:PA=PB=PC.
∴PA=PB=PC.
A
C
B
M
P
N
M'
N'
证明: ∵点P在线段AB的垂直平分线上,点P在线段BC的垂直平分线上(已知)
∴PA=PB ,PB=PC(线段垂直平分线上的点到线段两端的距离相等)
四、典型例题
总结:在△ABC中,若AB、BC的垂直平分线相交于点P,则点P也在AC的垂直平分线上.
归纳:
四、典型例题
三角形三边的垂直平分线相交于一点,这点到三角形三个顶点的距离相等.
线段垂直平分线的判定:
到线段两端距离相等的点在线段的垂直平分线上.
作用:判断一个点是否在线段的垂直平分线上.
D
【当堂检测】
4.如图,在△ABC中,分别以点A,B为圆心,大于 AB长为半径画弧,两弧分别交于点D,E,则直线DE是( )
A. ∠A的平分线 B. AC边的中线
C. BC边的高线 D. AB边的垂直平分线
解:分别以点A,B为圆心,大于 AB长为半径画弧,两弧分别交于点D,E.
∴DA=DB,EA=EB,
∴点D,E在线段AB的垂直平分线上.
【当堂检测】
5.已知:如图,点C,D是线段AB外的两点,且AC=BC,AD=BD,AB与CD相交于点O.求证:AO=BO.
证明:∵AC=BC,AD=BD,
∴点C和点D在线段AB的垂直平分线上,
∴CD为线段AB的垂直平分线.
又∵AB与CD相交于点O,
∴AO=BO.
五、课堂总结
画法:尺规作图
线段的垂直平分线
定理1:线段的垂直平分线上的点到线段的两端的距离相等;
定理2:到线段的两端距离相等的点在线段的垂直平分线上.
