14.1 全等三角形(第1课时)课件 20张PPT 沪科版八年级上册数学
文档属性
| 名称 | 14.1 全等三角形(第1课时)课件 20张PPT 沪科版八年级上册数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-21 10:44:41 | ||
图片预览







文档简介
(共20张PPT)
第十四章 全等三角形
14.1 全等三角形
1.知道全等形的概念,知道全等图形的性质;
2.理解全等三角形的概念,能找出两个全等三角形的对应顶点、对应角、对应边;(重点)
3.掌握全等三角形的性质,能利用性质解决简单的问题.(难点)
一、学习目标
二、新课导入
看一看:
从上面这三组图片中同学们看到了什么?每组图片它们之间有什么关系?
三、概念剖析
1.剪纸是我国民间的一种艺术,通过剪纸可以得到形状、大小完全相同的图形,下面两组图形是通过剪纸得到的,它们是完全重合的吗?
(一)全等三角形的概念
解:它们是完全重合的,是全等图形.
全等形:
三、概念剖析
2.结合前面的几组图形,你知道什么是全等图形了吗?它们有什么共同点?
(一)全等三角形的概念
全等形定义:能够完全重合的两个图形叫做全等形.
全等形性质:如果两个图形全等,它们的形状相同,大小相等.
总结:全等变化:一个图形经过平移、旋转、轴反射后,位置变化了,但形状和大小都没有改变,即平移、旋转、轴反射前后的两个图形全等。
三、概念剖析
1.观察下面两个全等三角形的形成过程,你能得到什么结论?请总结全等三角形的定义.
(一)全等三角形的概念
解:两个三角形完全重合;
全等三角形定义:能完全重合的两个三角形叫作全等三角形.
A
B
C
A
B
C
全等三角形:
三、概念剖析
2.全等三角形的相关概念:
(一)全等三角形的概念
全等的三角形中互相重合的顶点叫做对应顶点;互相重合的边叫做对应边;互相重合的角叫做对应角.“全等”用数学符号表达为≌,读作全等于,通常把表示对应顶点的字母写在对应位置上.
三、概念剖析
(一)全等三角形的概念
3.你还记得构成三角形的要素有哪些吗?上面的两个全等三角形的互相重合的点、角、边又有什么关系?
解:有顶点、边、角;互相重合的点一一对应、互相重合的角和边对应相等.
三、概念剖析
(一)全等三角形的概念
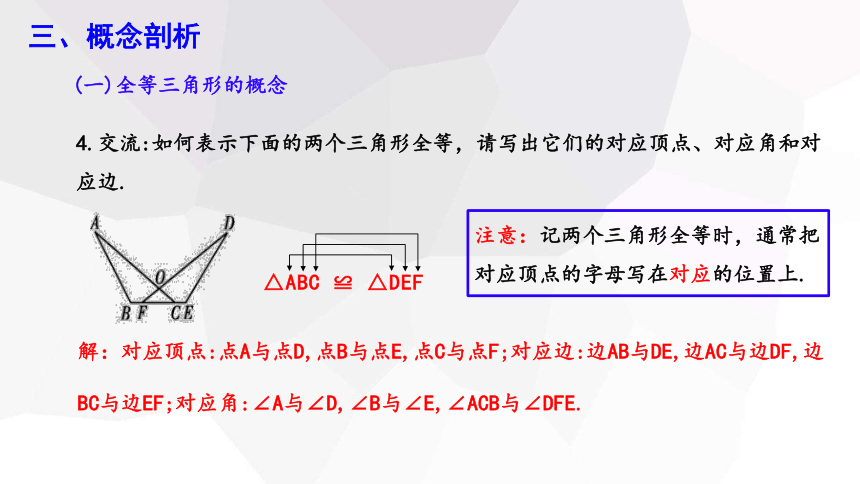
△ABC ≌ △DEF
4.交流:如何表示下面的两个三角形全等,请写出它们的对应顶点、对应角和对应边.
解:对应顶点:点A与点D,点B与点E,点C与点F;对应边:边AB与DE,边AC与边DF,边BC与边EF;对应角:∠A与∠D,∠B与∠E,∠ACB与∠DFE.
注意:记两个三角形全等时,通常把
对应顶点的字母写在对应的位置上.
三、概念剖析
归纳总结:
寻找对应元素的规律:
1.有公共边的,公共边是对应边;
2.有公共角的,公共角是对应角;
3.有对顶角的,对顶角是对应角;
4.两个全等三角形最大的边是对应边,最小的边也是对应边;
5.两个全等三角形最大的角是对应角,最小的角也是对应角.
三、概念剖析
1.思考:我们在上面的“交流”中找到了如图△ABC与△CED的对应边和对应角,我们由此可以得到全等三角形的什么性质?
(二)全等三角形的性质
解:全等三角形的对应边相等,对应角相等.
三、概念剖析
(二)全等三角形的性质
解:∵△ABC≌△DEF,
∴AB=DE,AC=DF,BC=EF(全等三角形对应边相等)
∠A=∠D,∠ABC=∠DEF,∠ACB=∠DFE
(全等三角形对应角相等)
2.全等三角形的性质的几何语言
注意:记两个全等三角形的对应边和对应角相等时,要参照两个全等三角形的记法,把对应相等顶点的字母写在对应的位置上.
四、典型例题
例1.下列各组图形中是全等图形的是 .
解:图④的两个图形形状相同,大小不相同,因此不是全等图形.
①
②
③
④
⑤
①,②,③,⑤
例2.如图,已知△ABC≌△DCB,AB=3,DB=4,∠A=60°.
(2)求AC,DC的长及∠D的度数.
D
A
C
B
O
解:对应边:AB与DC,AC与DB,BC与CB.
对应角:∠A与∠D,∠ABC与∠DCB,∠ACB与∠DBC.
解:∵△ABC≌△DCB,∴ AC=DB=4,DC=AB=3,∠D=∠A=60°.
(1)写出△ABC和△DCB的对应边和对应角;
四、典型例题
例3.如图,△ABC≌△AED,AB是△ABC的最大边,AE是△AED的最大边∠BAC与∠EAD是对应角,且∠BAC=25°,∠B=35°,AB=3cm,BC=1cm,求出∠E,∠ADE的度数和线段DE,AE的长度.
解:∵△ABC≌△AED,(已知)
∴∠E=∠B=35°,(全等三角形对应角相等)
∠ADE=∠ACB=180°-25°- 35°=120 °,
(全等三角形对应角相等)
∴DE=BC=1cm,AE=AB=3cm.(全等三角形对应边相等)
四、典型例题
B
C
E
D
A
【当堂检测】
1.下列说法:
①用同一张底片冲洗出来的10张1寸相片是全等形;②我国国旗上的4颗小五角星是全等形;③所有的正方形是全等形;④全等形的面积一定相等.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
C
解:根据全等图形的性质进行判断:全等图形的形状、大小完全相同,可推出全等形的面积也相等,故①②④说法正确,③无法确定给出的正方形大小是一样的,因此不正确,故正确的有3个.
2.已知图中的两个三角形全等,则∠α的度数是 .
解:根据全等三角形的性质可知,如图的两个三角形的对应边相等,对应角相等,先找出对应相等的边,可确定对应相等的角,所以∠α=50°.
50°
【当堂检测】
3.如图,CD⊥AB于点D,BE⊥AC于点E, △ABE≌△ACD, ∠C=30°,AB=11,AD=3,
G为AB延长线上一点,求∠EBG的度数和CE的长.
分析:结合全等三角形的对应角相等的性质及外角或邻补角的知识,求得∠EBG的角度等于150°,利用全等三角形对应边相等的性质及等量减等量差相等的关系,可得CE = CA-AE= BA-AD =7.
【当堂检测】
3.如图,CD⊥AB于点D,BE⊥AC于点E, △ABE≌△ACD, ∠C=30°,AB=11,AD=3,
G为AB延长线上一点,求∠EBG的度数和CE的长.
解:∵△ABE≌△ABD,
∴∠EBA =∠C=30°, AC = AB = 11, AD=3.
∴CE = CA-AE = AB-AD = 7.
又∵∠EBG是三角形ABE的一个外角, ∴∠EBA+∠EBG=180°,∠EBG=180 °- 30°=150°
【当堂检测】
五、课堂总结
第十四章 全等三角形
14.1 全等三角形
1.知道全等形的概念,知道全等图形的性质;
2.理解全等三角形的概念,能找出两个全等三角形的对应顶点、对应角、对应边;(重点)
3.掌握全等三角形的性质,能利用性质解决简单的问题.(难点)
一、学习目标
二、新课导入
看一看:
从上面这三组图片中同学们看到了什么?每组图片它们之间有什么关系?
三、概念剖析
1.剪纸是我国民间的一种艺术,通过剪纸可以得到形状、大小完全相同的图形,下面两组图形是通过剪纸得到的,它们是完全重合的吗?
(一)全等三角形的概念
解:它们是完全重合的,是全等图形.
全等形:
三、概念剖析
2.结合前面的几组图形,你知道什么是全等图形了吗?它们有什么共同点?
(一)全等三角形的概念
全等形定义:能够完全重合的两个图形叫做全等形.
全等形性质:如果两个图形全等,它们的形状相同,大小相等.
总结:全等变化:一个图形经过平移、旋转、轴反射后,位置变化了,但形状和大小都没有改变,即平移、旋转、轴反射前后的两个图形全等。
三、概念剖析
1.观察下面两个全等三角形的形成过程,你能得到什么结论?请总结全等三角形的定义.
(一)全等三角形的概念
解:两个三角形完全重合;
全等三角形定义:能完全重合的两个三角形叫作全等三角形.
A
B
C
A
B
C
全等三角形:
三、概念剖析
2.全等三角形的相关概念:
(一)全等三角形的概念
全等的三角形中互相重合的顶点叫做对应顶点;互相重合的边叫做对应边;互相重合的角叫做对应角.“全等”用数学符号表达为≌,读作全等于,通常把表示对应顶点的字母写在对应位置上.
三、概念剖析
(一)全等三角形的概念
3.你还记得构成三角形的要素有哪些吗?上面的两个全等三角形的互相重合的点、角、边又有什么关系?
解:有顶点、边、角;互相重合的点一一对应、互相重合的角和边对应相等.
三、概念剖析
(一)全等三角形的概念
△ABC ≌ △DEF
4.交流:如何表示下面的两个三角形全等,请写出它们的对应顶点、对应角和对应边.
解:对应顶点:点A与点D,点B与点E,点C与点F;对应边:边AB与DE,边AC与边DF,边BC与边EF;对应角:∠A与∠D,∠B与∠E,∠ACB与∠DFE.
注意:记两个三角形全等时,通常把
对应顶点的字母写在对应的位置上.
三、概念剖析
归纳总结:
寻找对应元素的规律:
1.有公共边的,公共边是对应边;
2.有公共角的,公共角是对应角;
3.有对顶角的,对顶角是对应角;
4.两个全等三角形最大的边是对应边,最小的边也是对应边;
5.两个全等三角形最大的角是对应角,最小的角也是对应角.
三、概念剖析
1.思考:我们在上面的“交流”中找到了如图△ABC与△CED的对应边和对应角,我们由此可以得到全等三角形的什么性质?
(二)全等三角形的性质
解:全等三角形的对应边相等,对应角相等.
三、概念剖析
(二)全等三角形的性质
解:∵△ABC≌△DEF,
∴AB=DE,AC=DF,BC=EF(全等三角形对应边相等)
∠A=∠D,∠ABC=∠DEF,∠ACB=∠DFE
(全等三角形对应角相等)
2.全等三角形的性质的几何语言
注意:记两个全等三角形的对应边和对应角相等时,要参照两个全等三角形的记法,把对应相等顶点的字母写在对应的位置上.
四、典型例题
例1.下列各组图形中是全等图形的是 .
解:图④的两个图形形状相同,大小不相同,因此不是全等图形.
①
②
③
④
⑤
①,②,③,⑤
例2.如图,已知△ABC≌△DCB,AB=3,DB=4,∠A=60°.
(2)求AC,DC的长及∠D的度数.
D
A
C
B
O
解:对应边:AB与DC,AC与DB,BC与CB.
对应角:∠A与∠D,∠ABC与∠DCB,∠ACB与∠DBC.
解:∵△ABC≌△DCB,∴ AC=DB=4,DC=AB=3,∠D=∠A=60°.
(1)写出△ABC和△DCB的对应边和对应角;
四、典型例题
例3.如图,△ABC≌△AED,AB是△ABC的最大边,AE是△AED的最大边∠BAC与∠EAD是对应角,且∠BAC=25°,∠B=35°,AB=3cm,BC=1cm,求出∠E,∠ADE的度数和线段DE,AE的长度.
解:∵△ABC≌△AED,(已知)
∴∠E=∠B=35°,(全等三角形对应角相等)
∠ADE=∠ACB=180°-25°- 35°=120 °,
(全等三角形对应角相等)
∴DE=BC=1cm,AE=AB=3cm.(全等三角形对应边相等)
四、典型例题
B
C
E
D
A
【当堂检测】
1.下列说法:
①用同一张底片冲洗出来的10张1寸相片是全等形;②我国国旗上的4颗小五角星是全等形;③所有的正方形是全等形;④全等形的面积一定相等.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
C
解:根据全等图形的性质进行判断:全等图形的形状、大小完全相同,可推出全等形的面积也相等,故①②④说法正确,③无法确定给出的正方形大小是一样的,因此不正确,故正确的有3个.
2.已知图中的两个三角形全等,则∠α的度数是 .
解:根据全等三角形的性质可知,如图的两个三角形的对应边相等,对应角相等,先找出对应相等的边,可确定对应相等的角,所以∠α=50°.
50°
【当堂检测】
3.如图,CD⊥AB于点D,BE⊥AC于点E, △ABE≌△ACD, ∠C=30°,AB=11,AD=3,
G为AB延长线上一点,求∠EBG的度数和CE的长.
分析:结合全等三角形的对应角相等的性质及外角或邻补角的知识,求得∠EBG的角度等于150°,利用全等三角形对应边相等的性质及等量减等量差相等的关系,可得CE = CA-AE= BA-AD =7.
【当堂检测】
3.如图,CD⊥AB于点D,BE⊥AC于点E, △ABE≌△ACD, ∠C=30°,AB=11,AD=3,
G为AB延长线上一点,求∠EBG的度数和CE的长.
解:∵△ABE≌△ABD,
∴∠EBA =∠C=30°, AC = AB = 11, AD=3.
∴CE = CA-AE = AB-AD = 7.
又∵∠EBG是三角形ABE的一个外角, ∴∠EBA+∠EBG=180°,∠EBG=180 °- 30°=150°
【当堂检测】
五、课堂总结
