13.2 命题与证明 (第3课时) 课件 15张PPT 沪科版八年级上册数学
文档属性
| 名称 | 13.2 命题与证明 (第3课时) 课件 15张PPT 沪科版八年级上册数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 245.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-21 11:09:31 | ||
图片预览






文档简介
(共15张PPT)
13.2.3 分析与证明
第十三章 三角形中的边角关系、命题与证明
13.2 命题与证明
1.能分清一个问题的已知、求证、因果关系;
2.会用分析法对一个证明题进行分析,找出证明途径;(重点)
一、学习目标
3.能用几何语言准确地写出一个问题的证明过程,并符合书写
规范.(难点)
二、新课导入
回顾:什么是演绎推理,什么是证明吗?
从已知条件出发,依据定义、基本事实、已证定理,并按照逻辑
规则,推导出结论,这一方法称为演绎推理(或演绎法).演绎推理的过
程,就是演绎证明,简称证明.
注意:证明中的每一部推理都要有根据,不能想当然.这些根据,
可以是已知条件,也可以是定义、公理、已经学过的定理.
二、新课导入
上节课,我们知道了什么是证明,证明一般的书写规范与几何语言是怎样的.
这节课,我们就来学习,如何分析一个需要证明的问题.找到已知条件与要证结
论之间的联系.分析法是常用的方法之一.
我们先通过一道例题来体会分析的过程.
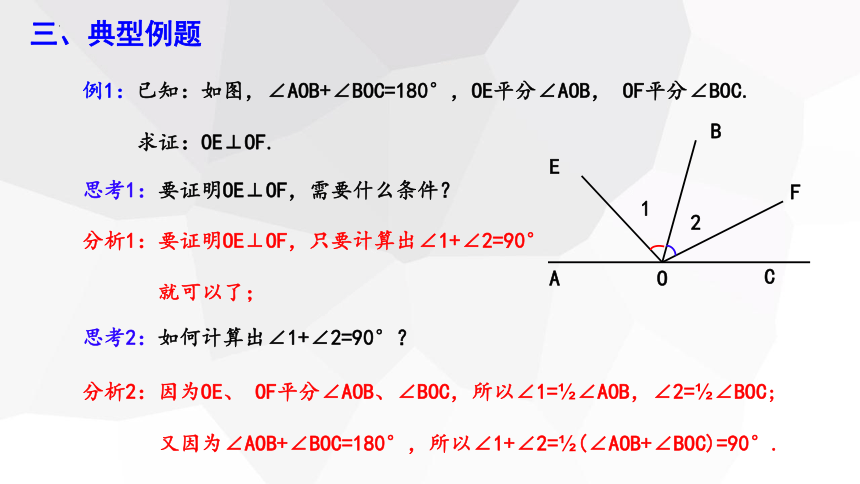
例1:已知:如图,∠AOB+∠BOC=180°,OE平分∠AOB, OF平分∠BOC.
求证:OE⊥OF.
三、典型例题
A
O
C
E
B
F
1
2
思考1:要证明OE⊥OF,需要什么条件?
分析1:要证明OE⊥OF,只要计算出∠1+∠2=90°
就可以了;
思考2:如何计算出∠1+∠2=90°?
分析2:因为OE、 OF平分∠AOB、∠BOC,所以∠1= ∠AOB,∠2= ∠BOC;
又因为∠AOB+∠BOC=180°,所以∠1+∠2= (∠AOB+∠BOC)=90°.
A
O
C
E
B
F
1
2
分析结束,接下来写出证明步骤.
证明: ∵ OE平分∠AOB,OF平分∠BOC,(已知)
∴∠1= ∠AOB,∠2= ∠BOC.(角平分线的定义)
又∵∠AOB+∠BOC=180°,(已知)
∴∠1+∠2= (∠AOB+∠BOC)=90°,(等式性质)
∴OE⊥OF.(垂直的定义)
思考:通过以上的证明过程,你能总结出证明命题的一般步骤吗?
三、典型例题
三、典型例题
证明命题的一般步骤:
2.根据题意,画出图形;(有些几何题目给出图形,该步骤可省略)
3.结合图形,用符号语言写出“已知”和“求证”;
5.依据思路,运用数学符号和数学语言条理清晰地写出证明过程.
1.理解题意:分清命题的条件(已知),结论(求证);
4.分析题意,探索证明思路;
总结:
1.补充完成下列两题的证明,并填上推理的依据.
(1)已知:如图,AB∥DC,AD∥BC. 求证:∠A=∠C.
【当堂检测】
证明:
∵AB∥DC,( )
∴∠A+∠D=180°.( )
∵AD∥BC,( )
等量代换
已知
两直线平行,同旁内角互补
A
B
C
D
∴ .( )
∴∠A+∠D=∠C+∠D.( )
∴∠A=∠C.( )
两直线平行,同旁内角互补
已知
∠C+∠D=180°
等量代换
(2)已知:如图,DC∥AB,DF平分∠CDB,BE平分∠ABD.
求证:∠1=∠2.
【当堂检测】
A
B
C
D
E
F
1
2
证明:
∵DC∥AB,( )
∴∠ABD=∠CDB.( )
又 ∵DF平分∠CDB,BE平分∠ABD( )
已知
两直线平行,内错角相等
∴∠1= ∠ ,( )
∠2= ∠ . ( )
∴∠1=∠2.( )
已知
等量代换
角平分线的定义
角平分线的定义
CDB
ABD
例2:求证对顶角相等.
三、典型例题
1.理解题意
已知:两个角是对顶角;求证:这两个角相等
2.画图形
A
B
C
D
O
画一对对顶角,如图所示
3.结合图形用符号语言写出已知和求证
已知:如图,直线AB与直线CD相交于点O,∠AOC与∠BOD是对顶角.
求证:∠AOC =∠BOD.
4.分析题意,探索证明思路
分析:观察图形可知,∠AOC+∠BOC=180°,∠BOD+∠BOC=180°.
三、典型例题
A
B
C
D
O
5.写出证明过程.
证明:
∴ ∠AOB与∠COD都是平角,(平角的定义)
∴ ∠AOC+∠AOD=180°,∠BOD+∠AOD=180°.(补角的定义)
∵直线AB与直线CD相交于点O ,( 已知 )
∴ ∠BOD+∠AOD=180°.(等量代换)
1.求证在同平面内,垂直于同一条直线的两直线平行.
【当堂检测】
解:已知,如图直线a,b,c在同一平面内,a⊥c,b⊥c.
求证:a∥b.
1
2
a
b
c
证明: ∵ a⊥c,b⊥c,(已知)
∴∠1=90°,∠2=90°,(垂直的定义)
∴∠1=∠2,(等量代换)
∴ a∥b.(同位角相等,两直线平行)
分析:要证明a∥b,先要证明∠1=∠2.
2. 已知,如图,AB⊥BF, CD⊥BF,∠1=∠2.
求证: ∠3=∠4
【当堂检测】
分析:要证明∠3=∠4,先要证明CD∥EF.
根据AB⊥BF, CD⊥BF可得AB∥CD;
根据∠1=∠2,可得AB∥EF;
根据AB∥CD,AB∥EF可得CD∥EF.
1
2
3
4
A
B
C
D
E
F
【当堂检测】
证明:∵ AB⊥BF,CD⊥BF(已知)
∴∠ B=∠CDF=90°(垂线的定义)
∴AB∥CD(垂直于同一直线的两直线平行)
又∵∠1=∠2(已知)
∴AB//EF(内错角相等,两直线平行)
∴ CD∥EF(平行于同一直线的两直线平行)
∴∠3=∠4(两直线平行,同位角相等)
1
2
3
4
A
B
C
D
E
F
四、课堂总结
证明命题的一般步骤:
理解题意
画图形
写出已知和求证
分析
写出证明过程
13.2.3 分析与证明
第十三章 三角形中的边角关系、命题与证明
13.2 命题与证明
1.能分清一个问题的已知、求证、因果关系;
2.会用分析法对一个证明题进行分析,找出证明途径;(重点)
一、学习目标
3.能用几何语言准确地写出一个问题的证明过程,并符合书写
规范.(难点)
二、新课导入
回顾:什么是演绎推理,什么是证明吗?
从已知条件出发,依据定义、基本事实、已证定理,并按照逻辑
规则,推导出结论,这一方法称为演绎推理(或演绎法).演绎推理的过
程,就是演绎证明,简称证明.
注意:证明中的每一部推理都要有根据,不能想当然.这些根据,
可以是已知条件,也可以是定义、公理、已经学过的定理.
二、新课导入
上节课,我们知道了什么是证明,证明一般的书写规范与几何语言是怎样的.
这节课,我们就来学习,如何分析一个需要证明的问题.找到已知条件与要证结
论之间的联系.分析法是常用的方法之一.
我们先通过一道例题来体会分析的过程.
例1:已知:如图,∠AOB+∠BOC=180°,OE平分∠AOB, OF平分∠BOC.
求证:OE⊥OF.
三、典型例题
A
O
C
E
B
F
1
2
思考1:要证明OE⊥OF,需要什么条件?
分析1:要证明OE⊥OF,只要计算出∠1+∠2=90°
就可以了;
思考2:如何计算出∠1+∠2=90°?
分析2:因为OE、 OF平分∠AOB、∠BOC,所以∠1= ∠AOB,∠2= ∠BOC;
又因为∠AOB+∠BOC=180°,所以∠1+∠2= (∠AOB+∠BOC)=90°.
A
O
C
E
B
F
1
2
分析结束,接下来写出证明步骤.
证明: ∵ OE平分∠AOB,OF平分∠BOC,(已知)
∴∠1= ∠AOB,∠2= ∠BOC.(角平分线的定义)
又∵∠AOB+∠BOC=180°,(已知)
∴∠1+∠2= (∠AOB+∠BOC)=90°,(等式性质)
∴OE⊥OF.(垂直的定义)
思考:通过以上的证明过程,你能总结出证明命题的一般步骤吗?
三、典型例题
三、典型例题
证明命题的一般步骤:
2.根据题意,画出图形;(有些几何题目给出图形,该步骤可省略)
3.结合图形,用符号语言写出“已知”和“求证”;
5.依据思路,运用数学符号和数学语言条理清晰地写出证明过程.
1.理解题意:分清命题的条件(已知),结论(求证);
4.分析题意,探索证明思路;
总结:
1.补充完成下列两题的证明,并填上推理的依据.
(1)已知:如图,AB∥DC,AD∥BC. 求证:∠A=∠C.
【当堂检测】
证明:
∵AB∥DC,( )
∴∠A+∠D=180°.( )
∵AD∥BC,( )
等量代换
已知
两直线平行,同旁内角互补
A
B
C
D
∴ .( )
∴∠A+∠D=∠C+∠D.( )
∴∠A=∠C.( )
两直线平行,同旁内角互补
已知
∠C+∠D=180°
等量代换
(2)已知:如图,DC∥AB,DF平分∠CDB,BE平分∠ABD.
求证:∠1=∠2.
【当堂检测】
A
B
C
D
E
F
1
2
证明:
∵DC∥AB,( )
∴∠ABD=∠CDB.( )
又 ∵DF平分∠CDB,BE平分∠ABD( )
已知
两直线平行,内错角相等
∴∠1= ∠ ,( )
∠2= ∠ . ( )
∴∠1=∠2.( )
已知
等量代换
角平分线的定义
角平分线的定义
CDB
ABD
例2:求证对顶角相等.
三、典型例题
1.理解题意
已知:两个角是对顶角;求证:这两个角相等
2.画图形
A
B
C
D
O
画一对对顶角,如图所示
3.结合图形用符号语言写出已知和求证
已知:如图,直线AB与直线CD相交于点O,∠AOC与∠BOD是对顶角.
求证:∠AOC =∠BOD.
4.分析题意,探索证明思路
分析:观察图形可知,∠AOC+∠BOC=180°,∠BOD+∠BOC=180°.
三、典型例题
A
B
C
D
O
5.写出证明过程.
证明:
∴ ∠AOB与∠COD都是平角,(平角的定义)
∴ ∠AOC+∠AOD=180°,∠BOD+∠AOD=180°.(补角的定义)
∵直线AB与直线CD相交于点O ,( 已知 )
∴ ∠BOD+∠AOD=180°.(等量代换)
1.求证在同平面内,垂直于同一条直线的两直线平行.
【当堂检测】
解:已知,如图直线a,b,c在同一平面内,a⊥c,b⊥c.
求证:a∥b.
1
2
a
b
c
证明: ∵ a⊥c,b⊥c,(已知)
∴∠1=90°,∠2=90°,(垂直的定义)
∴∠1=∠2,(等量代换)
∴ a∥b.(同位角相等,两直线平行)
分析:要证明a∥b,先要证明∠1=∠2.
2. 已知,如图,AB⊥BF, CD⊥BF,∠1=∠2.
求证: ∠3=∠4
【当堂检测】
分析:要证明∠3=∠4,先要证明CD∥EF.
根据AB⊥BF, CD⊥BF可得AB∥CD;
根据∠1=∠2,可得AB∥EF;
根据AB∥CD,AB∥EF可得CD∥EF.
1
2
3
4
A
B
C
D
E
F
【当堂检测】
证明:∵ AB⊥BF,CD⊥BF(已知)
∴∠ B=∠CDF=90°(垂线的定义)
∴AB∥CD(垂直于同一直线的两直线平行)
又∵∠1=∠2(已知)
∴AB//EF(内错角相等,两直线平行)
∴ CD∥EF(平行于同一直线的两直线平行)
∴∠3=∠4(两直线平行,同位角相等)
1
2
3
4
A
B
C
D
E
F
四、课堂总结
证明命题的一般步骤:
理解题意
画图形
写出已知和求证
分析
写出证明过程
