13.1 三角形中的边角关系 (第2课时) 课件 17张PPT 沪科版八年级上册数学
文档属性
| 名称 | 13.1 三角形中的边角关系 (第2课时) 课件 17张PPT 沪科版八年级上册数学 |  | |
| 格式 | pptx | ||
| 文件大小 | 268.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-21 11:16:19 | ||
图片预览




文档简介
(共17张PPT)
第十三章 三角形中的边角关系、命题与证明
13.1三角形中的边角关系 第2课时
1.会按角将三角形分类;
2.掌握三角形内角和定理;(重点)
一、学习目标
3.能用三角形内角和定理解决相关问题.(难点)
二、新课导入
回顾:
A
B
C
内角
1.三角形内角的定义:
在一个三角形中,相邻两边组成的角叫做三角形的内角,如图所示.
2.三角形按边分类:
三角形按分类分为:等腰三角形、等边三角形和不等边三角形.
其中等边三角形是特殊的等腰三角形.
那么如果三角按角进行分类,能分为哪几种呢?
三、概念剖析
在小学我们已经学习了钝角、锐角、直角.
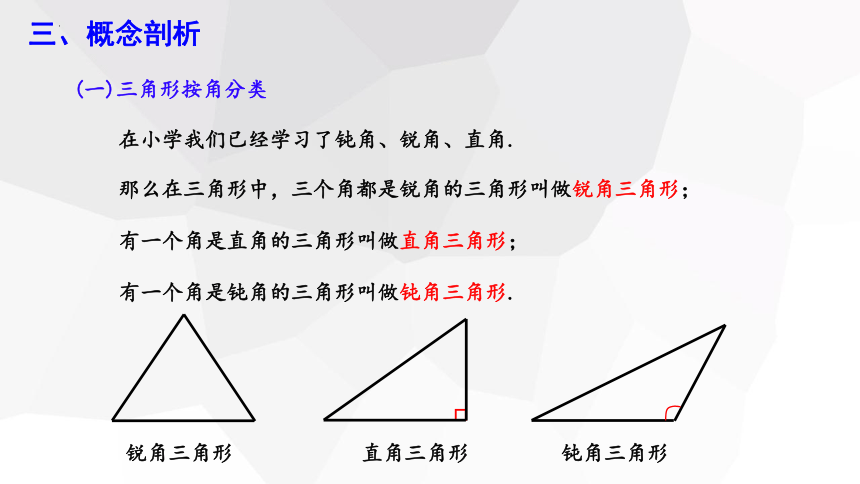
那么在三角形中,三个角都是锐角的三角形叫做锐角三角形;
有一个角是直角的三角形叫做直角三角形;
有一个角是钝角的三角形叫做钝角三角形.
锐角三角形
直角三角形
钝角三角形
(一)三角形按角分类
三、概念剖析
直角三角形中夹直角的两边叫做直角边,直角相对的边
叫斜边,直角三角形ABC可以写成Rt△ABC.
直角边
斜边
三角形按角的大小,可分为:
三角形
直角三角形
斜三角形
锐角三角形
钝角三角形
直角三角形
锐角
三角形
钝角
三角形
也可分为:
思考:根据以上的内容,谈谈你对三角形按角分类的想法.
三、概念剖析
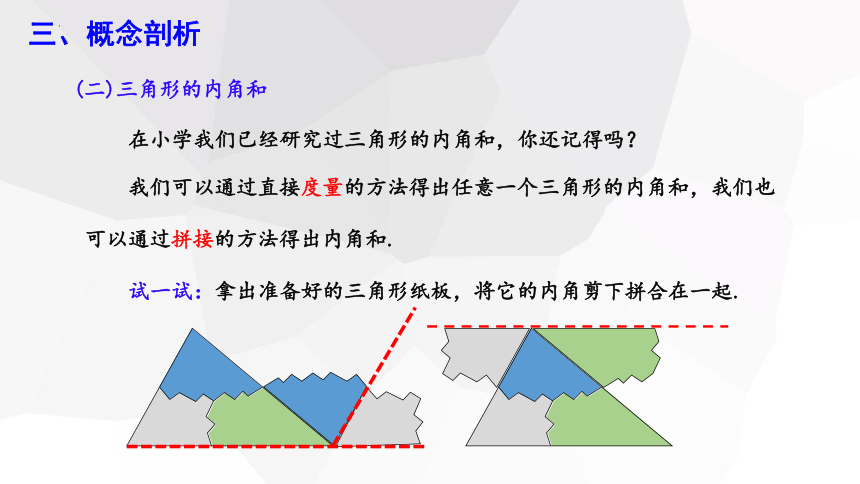
我们可以通过直接度量的方法得出任意一个三角形的内角和,我们也
可以通过拼接的方法得出内角和.
试一试:拿出准备好的三角形纸板,将它的内角剪下拼合在一起.
(二)三角形的内角和
在小学我们已经研究过三角形的内角和,你还记得吗?
三、概念剖析
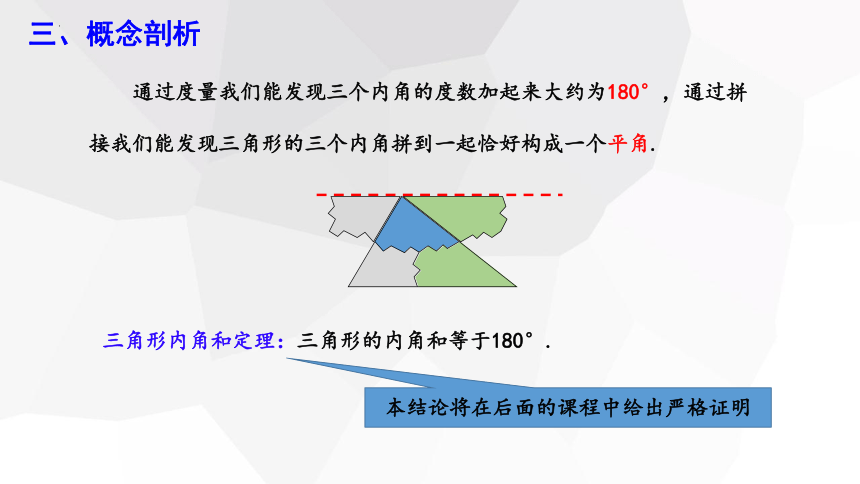
通过度量我们能发现三个内角的度数加起来大约为180°,通过拼
接我们能发现三角形的三个内角拼到一起恰好构成一个平角.
三角形内角和定理:三角形的内角和等于180°.
本结论将在后面的课程中给出严格证明
例1.一个三角形三个内角度数的比是3:5:4,那么这个三角形是锐角三角形、直角三角形、钝角三角形中的哪种?
解:依题意,设三角形的三个内角分别为:3x,5x,4x,
∴3x+5x+4x=180°,解得x=15°.
∴这个三角形三个角分别是:45°、75°、60°;
∴这个三角形是锐角三角形.
四、典型例题
分析:三角形内角和等于180°,已知三个内角关系可列方程求解.
【当堂检测】
1.填空.
(1)在△ABC中,∠A=35°,∠B=40 °,则△ABC是 三角形.
(2)在△ABC中,∠A:∠B:∠C=1:2:3,则△ABC是 三角形.
钝角
直角
2. 如图,在∠ACB=90 °, CD⊥AB,垂足是D.写出图中
所有直角三角形,并指出它们的斜边.
A
B
C
D
解:直角三角形有:(1)Rt△ABC,斜边为AB;
(2)Rt△ACD,斜边为AC;
(3)Rt△BCD,斜边为BC.
【当堂检测】
四、典型例题
例2. 如图,在△ABC中, ∠BAC=50 °, ∠B-∠C=10 °,∠CAD=∠BAD,
求∠ADB的度数.
A
B
C
D
解:由∠BAC=50 °, ∠CAD=∠BAD,得
∠BAD= ∠BAC=25°.
在△ABC中,∠BAC+∠B+∠C=180°.
在△ABD中,∠ADB=180°-∠B-∠BAD=180°-70°-25°=85°.
又∵∠BAC=50°,∠B-∠C=10 °;∴50°+∠B+(∠B-10°)=180°,
解得∠B=70°.
四、典型例题
例3. 如图,CE⊥AF,垂足为E,CE与BF相交于点D,
∠F=45°,∠FBA=75°, 求∠C的度数.
A
B
C
D
E
F
分析:根据三角形内角和定理,先求∠A的度数,
再求∠C的度数.
解:∵∠F=45°,∠FBA=75°,
∴在△AFB中,∠A=180°-75°-45°=60°,
又∵CE⊥AF,
∴△ACE中,∠C=180°-90°-60°=30°.
四、典型例题
如图,由三角形的内角和定理易推得∠1+∠2=∠3+∠4.
总结:
1
2
4
3
1
2
4
3
2
3
3. 已知:如图,在△ABC中,∠A=60°,∠C=70°,点D、E分别在AB和AC上,且DE∥BC.则∠ADE的度数是( )
A.40° B.50°
C.60° D.70°
【当堂检测】
A
B
C
E
D
B
【当堂检测】
4.如图,在△ABC中,∠C=78°,沿图中虚线截去∠C,则∠1+∠2=( )
A.282° B.360°
C.180° D.258°
D
C
A
B
1
2
四、典型例题
例4. 在三角形中,最多只可能有一个直角或钝角,为什么?
解:(1)假如在一个三角形中有两个直角,
根据三角形内角和定理,那么第3个角的度数为0;显然不成立.
(2)假如在一个三角形中有两个钝角,
根据三角形内角和定理,那么第3个角的度数为负数;也不成立.
结论:据此答案,我们发现一个三角形至少有两个锐角.
五、课堂总结
三角形
直角三角形
斜三角形
锐角三角形
钝角三角形
直角三角形
锐角
三角形
钝角
三角形
1.三角形按角的大小分类如下:
2.三角形内角和定理:
三角形的内角和等于180°.
第十三章 三角形中的边角关系、命题与证明
13.1三角形中的边角关系 第2课时
1.会按角将三角形分类;
2.掌握三角形内角和定理;(重点)
一、学习目标
3.能用三角形内角和定理解决相关问题.(难点)
二、新课导入
回顾:
A
B
C
内角
1.三角形内角的定义:
在一个三角形中,相邻两边组成的角叫做三角形的内角,如图所示.
2.三角形按边分类:
三角形按分类分为:等腰三角形、等边三角形和不等边三角形.
其中等边三角形是特殊的等腰三角形.
那么如果三角按角进行分类,能分为哪几种呢?
三、概念剖析
在小学我们已经学习了钝角、锐角、直角.
那么在三角形中,三个角都是锐角的三角形叫做锐角三角形;
有一个角是直角的三角形叫做直角三角形;
有一个角是钝角的三角形叫做钝角三角形.
锐角三角形
直角三角形
钝角三角形
(一)三角形按角分类
三、概念剖析
直角三角形中夹直角的两边叫做直角边,直角相对的边
叫斜边,直角三角形ABC可以写成Rt△ABC.
直角边
斜边
三角形按角的大小,可分为:
三角形
直角三角形
斜三角形
锐角三角形
钝角三角形
直角三角形
锐角
三角形
钝角
三角形
也可分为:
思考:根据以上的内容,谈谈你对三角形按角分类的想法.
三、概念剖析
我们可以通过直接度量的方法得出任意一个三角形的内角和,我们也
可以通过拼接的方法得出内角和.
试一试:拿出准备好的三角形纸板,将它的内角剪下拼合在一起.
(二)三角形的内角和
在小学我们已经研究过三角形的内角和,你还记得吗?
三、概念剖析
通过度量我们能发现三个内角的度数加起来大约为180°,通过拼
接我们能发现三角形的三个内角拼到一起恰好构成一个平角.
三角形内角和定理:三角形的内角和等于180°.
本结论将在后面的课程中给出严格证明
例1.一个三角形三个内角度数的比是3:5:4,那么这个三角形是锐角三角形、直角三角形、钝角三角形中的哪种?
解:依题意,设三角形的三个内角分别为:3x,5x,4x,
∴3x+5x+4x=180°,解得x=15°.
∴这个三角形三个角分别是:45°、75°、60°;
∴这个三角形是锐角三角形.
四、典型例题
分析:三角形内角和等于180°,已知三个内角关系可列方程求解.
【当堂检测】
1.填空.
(1)在△ABC中,∠A=35°,∠B=40 °,则△ABC是 三角形.
(2)在△ABC中,∠A:∠B:∠C=1:2:3,则△ABC是 三角形.
钝角
直角
2. 如图,在∠ACB=90 °, CD⊥AB,垂足是D.写出图中
所有直角三角形,并指出它们的斜边.
A
B
C
D
解:直角三角形有:(1)Rt△ABC,斜边为AB;
(2)Rt△ACD,斜边为AC;
(3)Rt△BCD,斜边为BC.
【当堂检测】
四、典型例题
例2. 如图,在△ABC中, ∠BAC=50 °, ∠B-∠C=10 °,∠CAD=∠BAD,
求∠ADB的度数.
A
B
C
D
解:由∠BAC=50 °, ∠CAD=∠BAD,得
∠BAD= ∠BAC=25°.
在△ABC中,∠BAC+∠B+∠C=180°.
在△ABD中,∠ADB=180°-∠B-∠BAD=180°-70°-25°=85°.
又∵∠BAC=50°,∠B-∠C=10 °;∴50°+∠B+(∠B-10°)=180°,
解得∠B=70°.
四、典型例题
例3. 如图,CE⊥AF,垂足为E,CE与BF相交于点D,
∠F=45°,∠FBA=75°, 求∠C的度数.
A
B
C
D
E
F
分析:根据三角形内角和定理,先求∠A的度数,
再求∠C的度数.
解:∵∠F=45°,∠FBA=75°,
∴在△AFB中,∠A=180°-75°-45°=60°,
又∵CE⊥AF,
∴△ACE中,∠C=180°-90°-60°=30°.
四、典型例题
如图,由三角形的内角和定理易推得∠1+∠2=∠3+∠4.
总结:
1
2
4
3
1
2
4
3
2
3
3. 已知:如图,在△ABC中,∠A=60°,∠C=70°,点D、E分别在AB和AC上,且DE∥BC.则∠ADE的度数是( )
A.40° B.50°
C.60° D.70°
【当堂检测】
A
B
C
E
D
B
【当堂检测】
4.如图,在△ABC中,∠C=78°,沿图中虚线截去∠C,则∠1+∠2=( )
A.282° B.360°
C.180° D.258°
D
C
A
B
1
2
四、典型例题
例4. 在三角形中,最多只可能有一个直角或钝角,为什么?
解:(1)假如在一个三角形中有两个直角,
根据三角形内角和定理,那么第3个角的度数为0;显然不成立.
(2)假如在一个三角形中有两个钝角,
根据三角形内角和定理,那么第3个角的度数为负数;也不成立.
结论:据此答案,我们发现一个三角形至少有两个锐角.
五、课堂总结
三角形
直角三角形
斜三角形
锐角三角形
钝角三角形
直角三角形
锐角
三角形
钝角
三角形
1.三角形按角的大小分类如下:
2.三角形内角和定理:
三角形的内角和等于180°.
