12.3 一次函数与二元一次方程 第2课时 课件(共22张PPT) 沪科版八年级上册数学
文档属性
| 名称 | 12.3 一次函数与二元一次方程 第2课时 课件(共22张PPT) 沪科版八年级上册数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 383.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-21 11:33:28 | ||
图片预览







文档简介
(共22张PPT)
第十二章 一次函数
12.3 一次函数与二元一次方程
第2课时 一次函数与二元一次方程组
1.知道一次函数与二元一次方程组的关系,会用图象法解二元一次方程组;
2.通过一次函数,了解二元一次方程组无解的情形;
3.会根据二元一次方程的系数判断二元一次方程组解的情况.
一、学习目标
二、新课导入
两条直线的交点是方程组的解.
思考:是不是任意两个一次函数图象的交点坐标都是它们所对应的二元一次方程组的解?
观察下列两条直线的图象:
它们的交点坐标A(-2,2)与方程组
有什么联系?
y=2x+6
1
-1
2
3
4
5
-4
-3
-2
-5
1
2
3
4
5
-1
-2
-3
-4
-5
0
x
6
-6
y=-2x-2
·
A(-2,2)
三、概念剖析
(一)一次函数与二元一次方程组的关系
确定两条直线交点的坐标,相当于求相应的二元一次方程组的解;解一个二元一次方程组相当于确定相应两条直线的交点的坐标.
二元一次方程组的解对应两个一次函数所在直线的交点坐标.
三、概念剖析
(二)二元一次方程组解的情况的判断
一次函数图象(两条直线)位置有三种关系及对应解的情况:
(1)相交(有一个交点) 二元一次方程组有唯一解;
(2)平行(无交点) 二元一次方程组无解;
(3)重合(有无数个交点) 二元一次方程组有无穷组解.
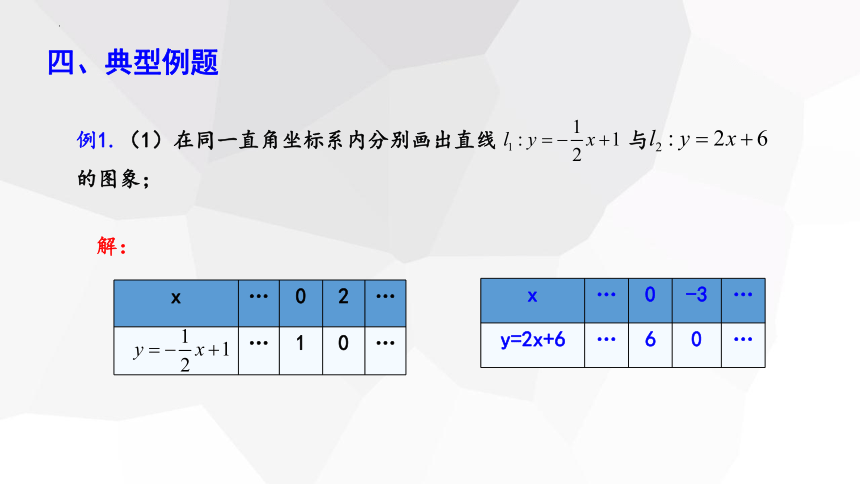
例1.(1)在同一直角坐标系内分别画出直线 与 的图象;
四、典型例题
解:
x … 0 2 …
… 1 0 …
x … 0 -3 …
y=2x+6 … 6 0 …
y
x
4
1
2
3
5
(-2,2)
-1
0
-2
-3
-4
1
2
3
4
5
6
y=2x+6
四、典型例题
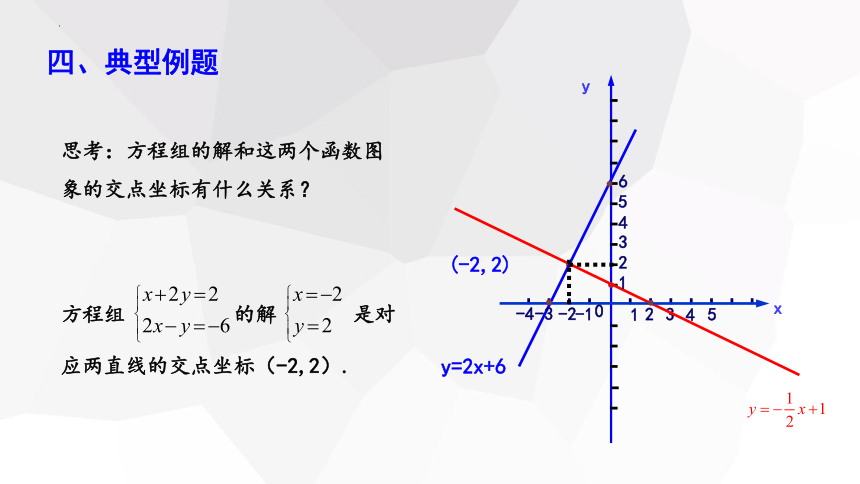
思考:方程组的解和这两个函数图象的交点坐标有什么关系?
方程组 的解 是对应两直线的交点坐标(-2,2).
四、典型例题
-2 2
(2)如果直线 与 相交于点P,写出点P的坐标( , );
解:(2)由图可知,直线 与 相交于点P,点P的坐标为(-2,2).
四、典型例题
(3)检验点P(-2,2)的坐标是不是下面方程组的解.
解:(3)方程x+2y=2可以转化成一次函数 的形式,因此,直线 上任意一点的坐标都是方程x+2y=2的解;
同理,直线 上任意坐标都是方程y=2x+6的解,所以两直线交点即方程组 的解.
总结:
确定两条直线交点的坐标,相当于求相应的二元一次方程组的解;解一个二元一次方程组相当于确定相应两条直线的交点的坐标.
四、典型例题
二元一次方程组的解
对应
两个一次函数所在直线的交点坐标
解方程组相当于考虑自变量为何值时,两个函数的值相等,以及这个函数值是何值.
【当堂检测】
A
1.二元一次方程组 的解为 ,则一次函数y=5-x与y=2x-1的交点坐标为( )
A.(2,3) B.(3,2)
C.(-2,3) D.(2,-3)
点拨:二元一次方程可以化为一次函数,两个二元一次方程组的解就是两个函数的交点坐标.
解析:∵二元一次方程组 的解为 ,
∴一次函数y=5-x与y=2x-1的交点坐标为(2,3)
【当堂检测】
(4,7)
点拨:本题考查了一次函数与二元一次方程组,函数图象交点坐标为两函数解析式组成的方程组的解.
2.直线y=x+3与y=2x-1的交点为 ,它可以看作是方程组
的解.
解:令x+3=2x-1,解得x=4,此时y=x+3=7,
∴直线y=x+3与y=2x-1的交点为(4,7),它可以看作是方程组
的解.
四、典型例题
解:对于方程5x-2y=4,有
例2.利用函数图象解方程组
3
-2
y
2
0
x
x
y
-2
2
-1
0
1
3
-1
-2
1
2
3
过(0,-2)和(2,3)画出方程5x-2y=4所对应的直线 .
同样,(0, -2)和(2, 3)也在表示方程10x-4y=8的直线上,所以方程①、 ②的图象都是通过(0, -2)和(2, 3)两点的直线 ,就是说,这两条直线重合.显然,直线 上每一个点的坐标都是原方程组的解,所以原方程组有无穷组解.
【当堂检测】
∴x=3,y=4同时满足两个函数解析式.
3.一次函数y=x+1和一次函数y=2x-2的图象的交点坐标是(3,4),则方程组 的解为 .
解:∵一次函数y=x+1和一次函数y=2x-2的图象的交点坐标是(3,4)
点拨:函数图象的交点坐标即为两函数解析式组成的方程组的解.
则 是二元一次方程组 即 的解.
4.用图象法解方程组 时,下列选项中的图象正确的是( )
A. B. C. D.
四、典型例题
C
解:由题意将函数 与函数y=-2x+4的图象分别在坐标轴上画出来,其交点就是方程组的解.
函数图象如图, 故选C项.
四、典型例题
例3.①利用函数图象解方程组
解:方程3x+2y=-2对应直线 .
方程6x+4y=4对应直线 .
作出直线 和 的图象如右图,
两条直线平行,故方程组无解.
·
·
·
·
四、典型例题
例3.②已知方程组的图象,你能利用图象法说出下面两个方程组的解吗?
无穷组解
方程组无解
四、典型例题
归纳总结:
二元一次方程组的解的情况有三种:
(1)图象相交时,原方程组有唯一组解;
(2)图象重合时,原方程组有无穷多组解;
(3)图象平行时,原方程组无解.
四、典型例题
①当 a1:a2 ≠b1:b2 时 ,两直线相交,故方程组有唯一解;
②当 a1:a2 =b1:b2 =c1 :c2时,两直线重合,故方程组有无穷组解;
③当a1:a2 =b1:b2 ≠c1 :c2时,两直线平行,故方程组无解.
思考:我们知道二元一次方程组的解的情况有三种.那么对于 ,当x、y的系数及常数项满足什么关系时,原方程组有唯一组解、有无穷组解、无解?
【当堂检测】
B
解析:二元一次方程组的解一般是指二元一次方程组的两个方程的公共解,也是两个一次函数所在直线的交点坐标.选项B中两直线平行,方程组无解,故选B项.
5.不解方程,下列方程组中无解的是( )
A. B.
C. D.
【当堂检测】
6.如图,求直线 与 的交点坐标.
O
y
x
解:因为直线 过点(-1,0),(0,2) ,用待定系数法可求得直线 的解析式为y=2x+2.同理可求得直线 的解析式为y=-x+3.
解方程组
得
即直线 与 的交点坐标为
五、课堂总结
二元一次方程组的解对应两个一次函数所在直线的交点坐标,解二元一次方程组相当于确定相应两条直线的交点的坐标.
一次函数与二元一次方程组
二元一次方程组的解的情况有三种:当两条直线相交时,原方程组有唯一组解;当两直线重合时,原方程组有无穷组解;当两直线图象平行时,原方程组无解.
第十二章 一次函数
12.3 一次函数与二元一次方程
第2课时 一次函数与二元一次方程组
1.知道一次函数与二元一次方程组的关系,会用图象法解二元一次方程组;
2.通过一次函数,了解二元一次方程组无解的情形;
3.会根据二元一次方程的系数判断二元一次方程组解的情况.
一、学习目标
二、新课导入
两条直线的交点是方程组的解.
思考:是不是任意两个一次函数图象的交点坐标都是它们所对应的二元一次方程组的解?
观察下列两条直线的图象:
它们的交点坐标A(-2,2)与方程组
有什么联系?
y=2x+6
1
-1
2
3
4
5
-4
-3
-2
-5
1
2
3
4
5
-1
-2
-3
-4
-5
0
x
6
-6
y=-2x-2
·
A(-2,2)
三、概念剖析
(一)一次函数与二元一次方程组的关系
确定两条直线交点的坐标,相当于求相应的二元一次方程组的解;解一个二元一次方程组相当于确定相应两条直线的交点的坐标.
二元一次方程组的解对应两个一次函数所在直线的交点坐标.
三、概念剖析
(二)二元一次方程组解的情况的判断
一次函数图象(两条直线)位置有三种关系及对应解的情况:
(1)相交(有一个交点) 二元一次方程组有唯一解;
(2)平行(无交点) 二元一次方程组无解;
(3)重合(有无数个交点) 二元一次方程组有无穷组解.
例1.(1)在同一直角坐标系内分别画出直线 与 的图象;
四、典型例题
解:
x … 0 2 …
… 1 0 …
x … 0 -3 …
y=2x+6 … 6 0 …
y
x
4
1
2
3
5
(-2,2)
-1
0
-2
-3
-4
1
2
3
4
5
6
y=2x+6
四、典型例题
思考:方程组的解和这两个函数图象的交点坐标有什么关系?
方程组 的解 是对应两直线的交点坐标(-2,2).
四、典型例题
-2 2
(2)如果直线 与 相交于点P,写出点P的坐标( , );
解:(2)由图可知,直线 与 相交于点P,点P的坐标为(-2,2).
四、典型例题
(3)检验点P(-2,2)的坐标是不是下面方程组的解.
解:(3)方程x+2y=2可以转化成一次函数 的形式,因此,直线 上任意一点的坐标都是方程x+2y=2的解;
同理,直线 上任意坐标都是方程y=2x+6的解,所以两直线交点即方程组 的解.
总结:
确定两条直线交点的坐标,相当于求相应的二元一次方程组的解;解一个二元一次方程组相当于确定相应两条直线的交点的坐标.
四、典型例题
二元一次方程组的解
对应
两个一次函数所在直线的交点坐标
解方程组相当于考虑自变量为何值时,两个函数的值相等,以及这个函数值是何值.
【当堂检测】
A
1.二元一次方程组 的解为 ,则一次函数y=5-x与y=2x-1的交点坐标为( )
A.(2,3) B.(3,2)
C.(-2,3) D.(2,-3)
点拨:二元一次方程可以化为一次函数,两个二元一次方程组的解就是两个函数的交点坐标.
解析:∵二元一次方程组 的解为 ,
∴一次函数y=5-x与y=2x-1的交点坐标为(2,3)
【当堂检测】
(4,7)
点拨:本题考查了一次函数与二元一次方程组,函数图象交点坐标为两函数解析式组成的方程组的解.
2.直线y=x+3与y=2x-1的交点为 ,它可以看作是方程组
的解.
解:令x+3=2x-1,解得x=4,此时y=x+3=7,
∴直线y=x+3与y=2x-1的交点为(4,7),它可以看作是方程组
的解.
四、典型例题
解:对于方程5x-2y=4,有
例2.利用函数图象解方程组
3
-2
y
2
0
x
x
y
-2
2
-1
0
1
3
-1
-2
1
2
3
过(0,-2)和(2,3)画出方程5x-2y=4所对应的直线 .
同样,(0, -2)和(2, 3)也在表示方程10x-4y=8的直线上,所以方程①、 ②的图象都是通过(0, -2)和(2, 3)两点的直线 ,就是说,这两条直线重合.显然,直线 上每一个点的坐标都是原方程组的解,所以原方程组有无穷组解.
【当堂检测】
∴x=3,y=4同时满足两个函数解析式.
3.一次函数y=x+1和一次函数y=2x-2的图象的交点坐标是(3,4),则方程组 的解为 .
解:∵一次函数y=x+1和一次函数y=2x-2的图象的交点坐标是(3,4)
点拨:函数图象的交点坐标即为两函数解析式组成的方程组的解.
则 是二元一次方程组 即 的解.
4.用图象法解方程组 时,下列选项中的图象正确的是( )
A. B. C. D.
四、典型例题
C
解:由题意将函数 与函数y=-2x+4的图象分别在坐标轴上画出来,其交点就是方程组的解.
函数图象如图, 故选C项.
四、典型例题
例3.①利用函数图象解方程组
解:方程3x+2y=-2对应直线 .
方程6x+4y=4对应直线 .
作出直线 和 的图象如右图,
两条直线平行,故方程组无解.
·
·
·
·
四、典型例题
例3.②已知方程组的图象,你能利用图象法说出下面两个方程组的解吗?
无穷组解
方程组无解
四、典型例题
归纳总结:
二元一次方程组的解的情况有三种:
(1)图象相交时,原方程组有唯一组解;
(2)图象重合时,原方程组有无穷多组解;
(3)图象平行时,原方程组无解.
四、典型例题
①当 a1:a2 ≠b1:b2 时 ,两直线相交,故方程组有唯一解;
②当 a1:a2 =b1:b2 =c1 :c2时,两直线重合,故方程组有无穷组解;
③当a1:a2 =b1:b2 ≠c1 :c2时,两直线平行,故方程组无解.
思考:我们知道二元一次方程组的解的情况有三种.那么对于 ,当x、y的系数及常数项满足什么关系时,原方程组有唯一组解、有无穷组解、无解?
【当堂检测】
B
解析:二元一次方程组的解一般是指二元一次方程组的两个方程的公共解,也是两个一次函数所在直线的交点坐标.选项B中两直线平行,方程组无解,故选B项.
5.不解方程,下列方程组中无解的是( )
A. B.
C. D.
【当堂检测】
6.如图,求直线 与 的交点坐标.
O
y
x
解:因为直线 过点(-1,0),(0,2) ,用待定系数法可求得直线 的解析式为y=2x+2.同理可求得直线 的解析式为y=-x+3.
解方程组
得
即直线 与 的交点坐标为
五、课堂总结
二元一次方程组的解对应两个一次函数所在直线的交点坐标,解二元一次方程组相当于确定相应两条直线的交点的坐标.
一次函数与二元一次方程组
二元一次方程组的解的情况有三种:当两条直线相交时,原方程组有唯一组解;当两直线重合时,原方程组有无穷组解;当两直线图象平行时,原方程组无解.
