4.1.2用二分法求方程的近似解
图片预览






文档简介
课件15张PPT。用二分法求方程的近似解知识探究(一):二分法的概念 思考1:从某水库闸房到防洪指挥部的某一处电话线路发生了故障。这是一条10km长的线路,如何迅速查出故障所在?思考2:已知函数 在区间(0,1)内有零点,你有什么方法求出这个零点的近似值(精确到0.01)? 解析解析如图,设闸门和指挥部的所在处为点A,B, B6.这样每查一次,就可以把待查的线路长度缩减一半
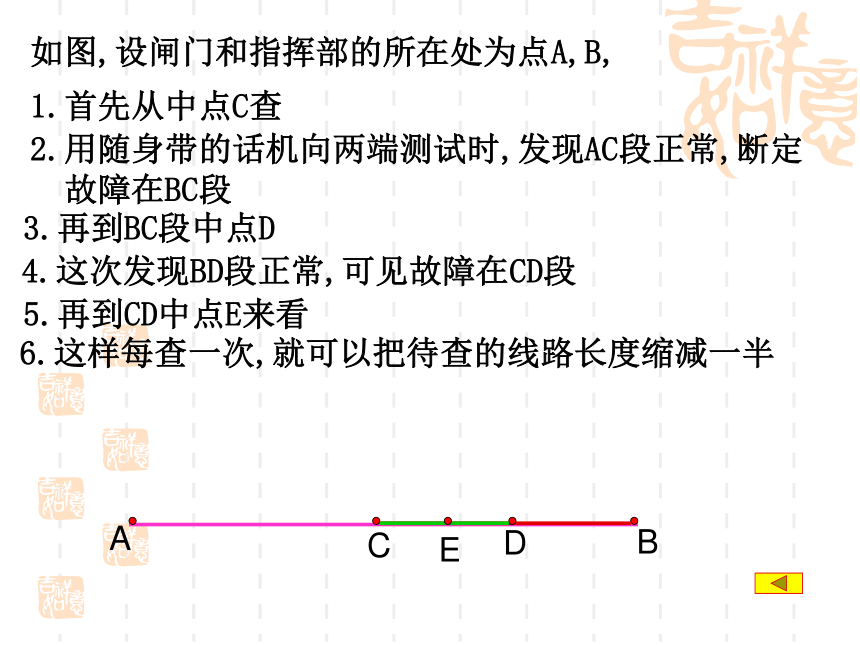
1.首先从中点C查2.用随身带的话机向两端测试时,发现AC段正常,断定
故障在BC段3.再到BC段中点D4.这次发现BD段正常,可见故障在CD段5.再到CD中点E来看思考2解析:怎样计算函数 在区间(0,1)内精确到0.01的零点近似值? (0,1) 0.5 -0.588 1 (0.5,1) 0.75 -0.134 0.5 (0.75,1) 0.875 0.0438 0.25(0.75,0.875) 0.8125 -0.042 0.125(0.8125,0.875) 0.84375 0.0017 0.0625(0.8125,0.84375) 0.828125 -0.020 0.03125(0.828125,0.84375) 0.8359375 -0.009 0.015625(0.8359375,0.84375) 0.83984375 -0.0036 0.0078125思考3:上述求函数零点近似值的方法叫做二分法,那么二分法的基本思想是什么? 对于在区间[a,b]上连续不断且f(a)·f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法. 知识探究(二):
用二分法求函数零点近似值的步骤 思考1:求函数f(x)的零点近似值第一步应做什么? 思考2:为了缩小零点所在区间的范围,接下来应做什么? 确定区间[a,b],使 f(a)f(b)<0 求区间的中点c,并计算f(c)的值 思考3:若f(c)=0说明什么? 若f(a)·f(c)<0或f(c)·f(b)<0 ,则分别说明什么? 若f(c)=0 ,则c就是函数的零点; 若f(a)·f(c)<0 ,则零点x0∈(a,c);若f(c)·f(b)<0 ,则零点x0∈(c,b).思考4:若给定精确度ε,如何选取近似值? 当|a—b|<ε时,区间[a,b]内的任意一个值都是函数零点的近似值. 不行,因为不满足 f(a)*f(b)<0例题分析例1 用二分法求方程 的近似解(精确到0.01).图片展示例2 求方程 的实根个数及其大致所在区间(精确到0.01).图片展示用二分法求函数零点近似值的基本步骤:3. 计算f(c):
(1)若f(c)=0,则c就是函数的零点;
(2)若f(a)·f(c)<0 ,则令b=c,此时零点 x0∈(a,c);
(3)若f(c)·f(b)<0 ,则令a=c,此时零点 x0∈(c,b). 2. 求区间(a,b)的中点c;1.确定区间[a,b],使f(a)·f(b)<0 ,给定精确度ε;4. 判断是否达到精确度ε:若 ,则得到零点近似值a(或b),一般用中点的近似值来作为零点的值;否则重复步骤2~4.作业
P119习题4.1A组:1,2,3,4题 找一个初始区间计算区间中点的函数值是否为0是结束运算否找出新的端点异号区间是否满足精确度是否流程图例1解:列表如下例2解:列表如下再见!
Good Bye!
1.首先从中点C查2.用随身带的话机向两端测试时,发现AC段正常,断定
故障在BC段3.再到BC段中点D4.这次发现BD段正常,可见故障在CD段5.再到CD中点E来看思考2解析:怎样计算函数 在区间(0,1)内精确到0.01的零点近似值? (0,1) 0.5 -0.588 1 (0.5,1) 0.75 -0.134 0.5 (0.75,1) 0.875 0.0438 0.25(0.75,0.875) 0.8125 -0.042 0.125(0.8125,0.875) 0.84375 0.0017 0.0625(0.8125,0.84375) 0.828125 -0.020 0.03125(0.828125,0.84375) 0.8359375 -0.009 0.015625(0.8359375,0.84375) 0.83984375 -0.0036 0.0078125思考3:上述求函数零点近似值的方法叫做二分法,那么二分法的基本思想是什么? 对于在区间[a,b]上连续不断且f(a)·f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法. 知识探究(二):
用二分法求函数零点近似值的步骤 思考1:求函数f(x)的零点近似值第一步应做什么? 思考2:为了缩小零点所在区间的范围,接下来应做什么? 确定区间[a,b],使 f(a)f(b)<0 求区间的中点c,并计算f(c)的值 思考3:若f(c)=0说明什么? 若f(a)·f(c)<0或f(c)·f(b)<0 ,则分别说明什么? 若f(c)=0 ,则c就是函数的零点; 若f(a)·f(c)<0 ,则零点x0∈(a,c);若f(c)·f(b)<0 ,则零点x0∈(c,b).思考4:若给定精确度ε,如何选取近似值? 当|a—b|<ε时,区间[a,b]内的任意一个值都是函数零点的近似值. 不行,因为不满足 f(a)*f(b)<0例题分析例1 用二分法求方程 的近似解(精确到0.01).图片展示例2 求方程 的实根个数及其大致所在区间(精确到0.01).图片展示用二分法求函数零点近似值的基本步骤:3. 计算f(c):
(1)若f(c)=0,则c就是函数的零点;
(2)若f(a)·f(c)<0 ,则令b=c,此时零点 x0∈(a,c);
(3)若f(c)·f(b)<0 ,则令a=c,此时零点 x0∈(c,b). 2. 求区间(a,b)的中点c;1.确定区间[a,b],使f(a)·f(b)<0 ,给定精确度ε;4. 判断是否达到精确度ε:若 ,则得到零点近似值a(或b),一般用中点的近似值来作为零点的值;否则重复步骤2~4.作业
P119习题4.1A组:1,2,3,4题 找一个初始区间计算区间中点的函数值是否为0是结束运算否找出新的端点异号区间是否满足精确度是否流程图例1解:列表如下例2解:列表如下再见!
Good Bye!
