2024湘教版数学七年级下册--第4章《相交线与平行线》素养综合检测(含解析)
文档属性
| 名称 | 2024湘教版数学七年级下册--第4章《相交线与平行线》素养综合检测(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 495.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2024湘教版数学七年级下册
第4章 相交线与平行线
第4章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共30分)
1.【定义法】给出下列说法:
(1)两条直线被第三条直线所截,同位角相等;
(2)平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交;
(3)相等的两个角是对顶角;
(4)从直线外一点到这条直线的垂线段,叫做这点到直线的距离.
其中正确的有( )
A.0个 B.1个 C.2个 D.3个
2.(2023湖南怀化中考)如图,平移直线AB至CD,直线AB,CD被直线EF所截,∠1=60°,则∠2的度数为( )
A.30° B.60°
C.100° D.120°
3.(2023湖北仙桃期中)如图,下列结论中错误的是( )
A.∠3与∠1是同位角
B.∠2与∠5是内错角
C.∠1与∠2是同旁内角
D.∠1与∠6是内错角
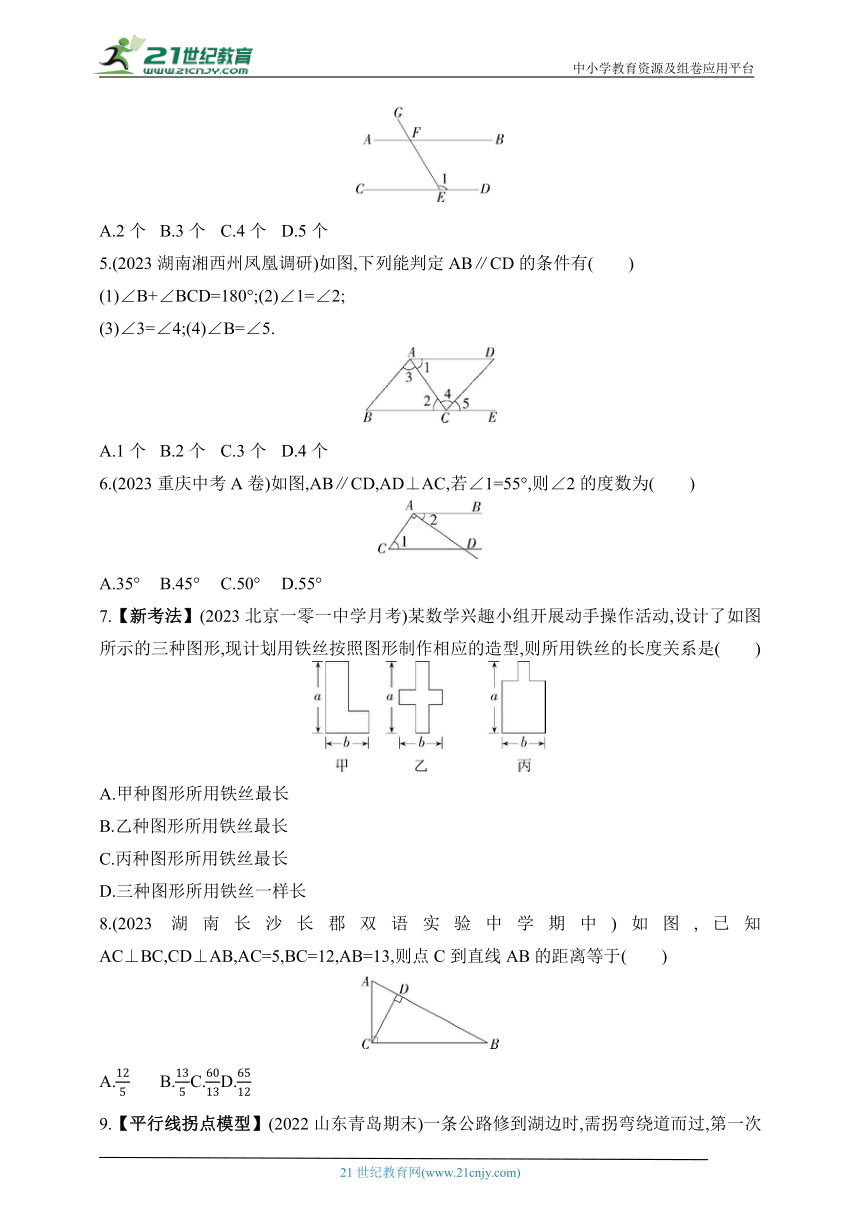
4.如图,已知AB∥CD,则图中与∠1互补的角有( )
A.2个 B.3个 C.4个 D.5个
5.(2023湖南湘西州凤凰调研)如图,下列能判定AB∥CD的条件有( )
(1)∠B+∠BCD=180°;(2)∠1=∠2;
(3)∠3=∠4;(4)∠B=∠5.
A.1个 B.2个 C.3个 D.4个
6.(2023重庆中考A卷)如图,AB∥CD,AD⊥AC,若∠1=55°,则∠2的度数为( )
A.35° B.45° C.50° D.55°
7.【新考法】(2023北京一零一中学月考)某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是( )
A.甲种图形所用铁丝最长
B.乙种图形所用铁丝最长
C.丙种图形所用铁丝最长
D.三种图形所用铁丝一样长
8.(2023湖南长沙长郡双语实验中学期中)如图,已知AC⊥BC,CD⊥AB,AC=5,BC=12,AB=13,则点C到直线AB的距离等于( )
A. B. C. D.
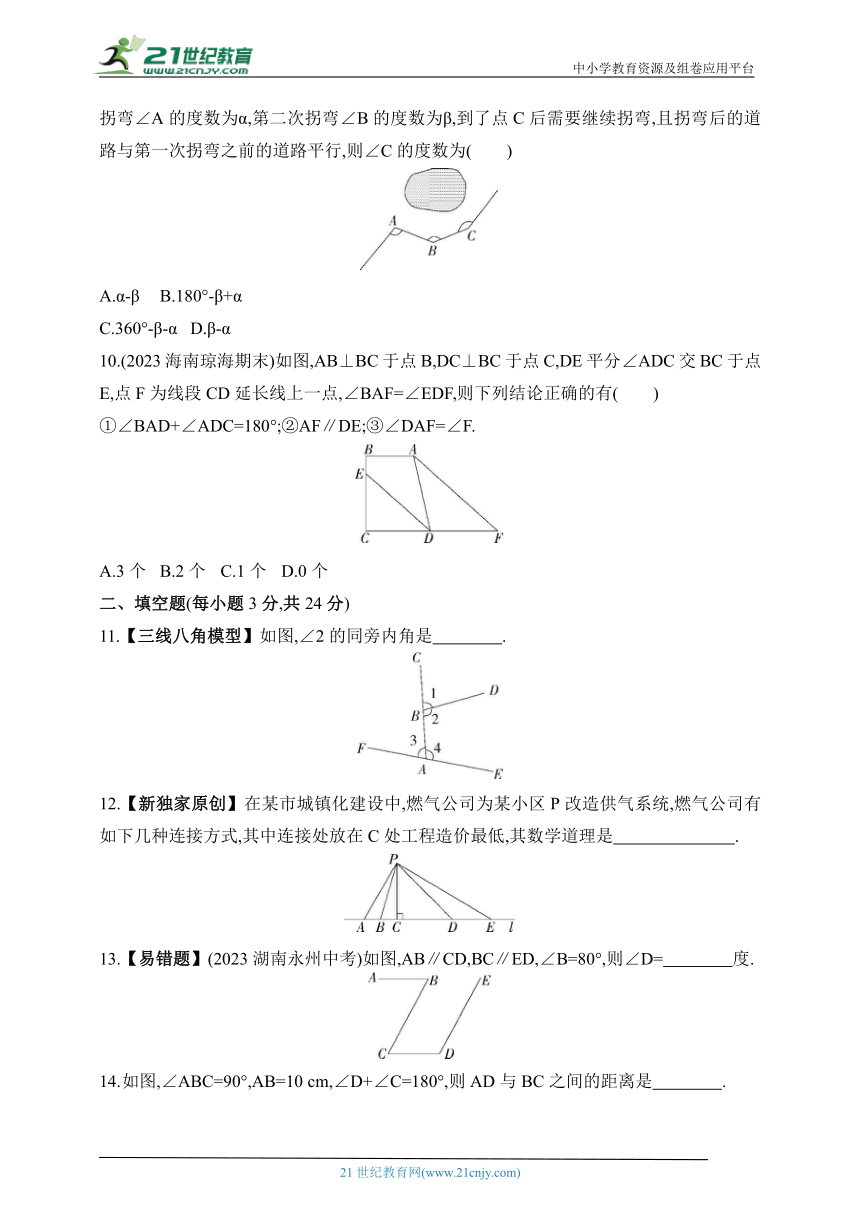
9.【平行线拐点模型】(2022山东青岛期末)一条公路修到湖边时,需拐弯绕道而过,第一次拐弯∠A的度数为α,第二次拐弯∠B的度数为β,到了点C后需要继续拐弯,且拐弯后的道路与第一次拐弯之前的道路平行,则∠C的度数为( )
A.α-β B.180°-β+α
C.360°-β-α D.β-α
10.(2023海南琼海期末)如图,AB⊥BC于点B,DC⊥BC于点C,DE平分∠ADC交BC于点E,点F为线段CD延长线上一点,∠BAF=∠EDF,则下列结论正确的有( )
①∠BAD+∠ADC=180°;②AF∥DE;③∠DAF=∠F.
A.3个 B.2个 C.1个 D.0个
二、填空题(每小题3分,共24分)
11.【三线八角模型】如图,∠2的同旁内角是 .
12.【新独家原创】在某市城镇化建设中,燃气公司为某小区P改造供气系统,燃气公司有如下几种连接方式,其中连接处放在C处工程造价最低,其数学道理是 .
13.【易错题】(2023湖南永州中考)如图,AB∥CD,BC∥ED,∠B=80°,则∠D= 度.
如图,∠ABC=90°,AB=10 cm,∠D+∠C=180°,则AD与BC之间的距离是 .
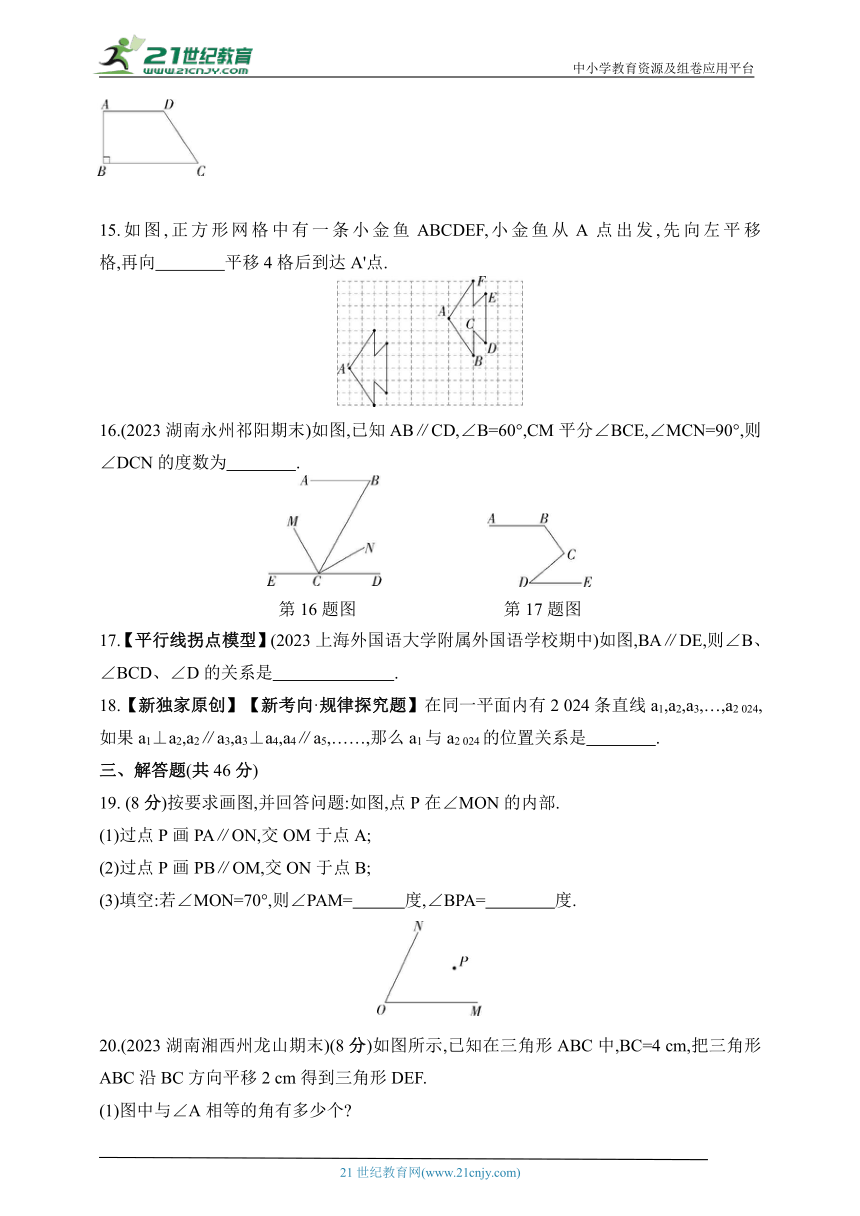
15.如图,正方形网格中有一条小金鱼ABCDEF,小金鱼从A点出发,先向左平移 格,再向 平移4格后到达A'点.
16.(2023湖南永州祁阳期末)如图,已知AB∥CD,∠B=60°,CM平分∠BCE,∠MCN=90°,则∠DCN的度数为 .
第16题图 第17题图
17.【平行线拐点模型】(2023上海外国语大学附属外国语学校期中)如图,BA∥DE,则∠B、∠BCD、∠D的关系是 .
18.【新独家原创】【新考向·规律探究题】在同一平面内有2 024条直线a1,a2,a3,…,a2 024,如果a1⊥a2,a2∥a3,a3⊥a4,a4∥a5,……,那么a1与a2 024的位置关系是 .
三、解答题(共46分)
19. (8分)按要求画图,并回答问题:如图,点P在∠MON的内部.
(1)过点P画PA∥ON,交OM于点A;
(2)过点P画PB∥OM,交ON于点B;
(3)填空:若∠MON=70°,则∠PAM= 度,∠BPA= 度.
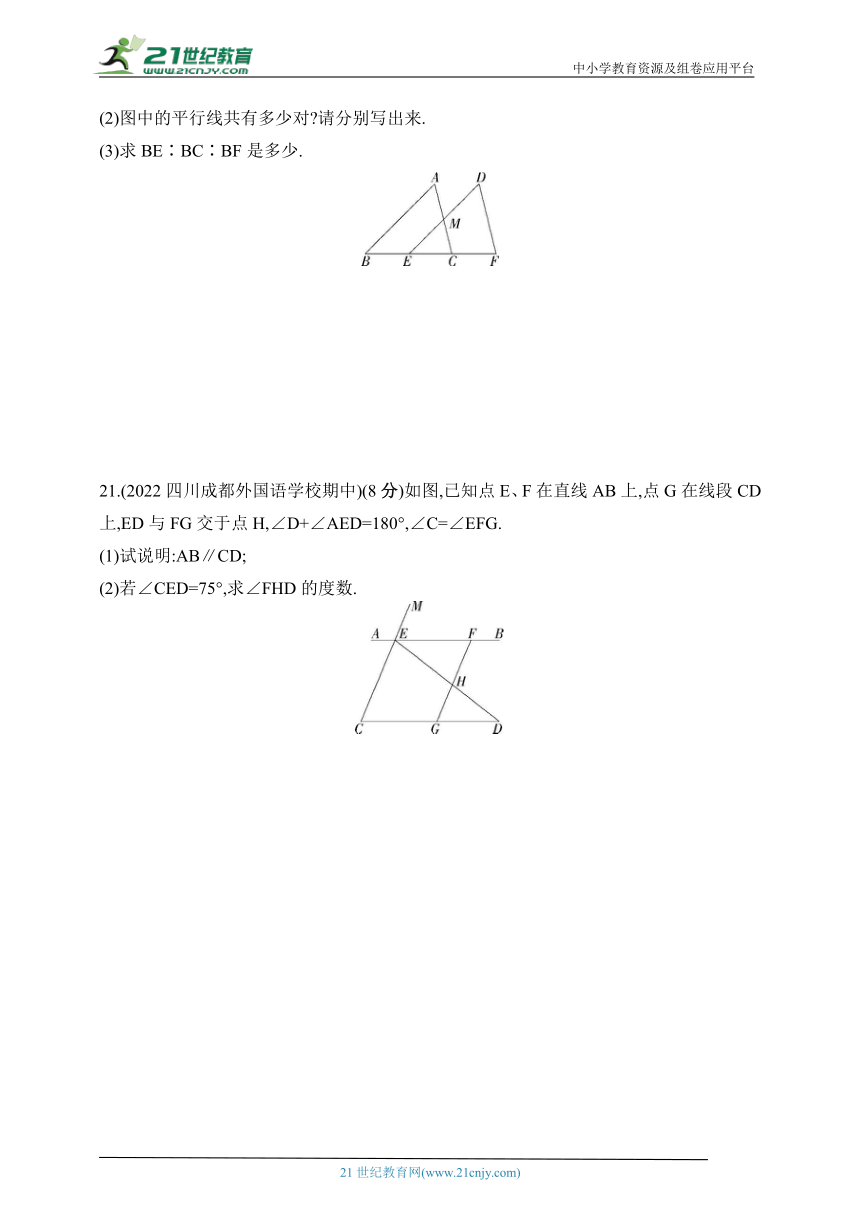
20.(2023湖南湘西州龙山期末)(8分)如图所示,已知在三角形ABC中,BC=4 cm,把三角形ABC沿BC方向平移2 cm得到三角形DEF.
(1)图中与∠A相等的角有多少个
(2)图中的平行线共有多少对 请分别写出来.
(3)求BE∶BC∶BF是多少.
21.(2022四川成都外国语学校期中)(8分)如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠D+∠AED=180°,∠C=∠EFG.
(1)试说明:AB∥CD;
(2)若∠CED=75°,求∠FHD的度数.
22.【分类讨论思想】(10分)如图,直线AB、CD相交于点O,OE平分∠BOC,∠BOD∶∠BOE=2∶3.
(1)求∠AOC的度数;
(2)过点O作OF⊥CD于点O,求∠AOF的度数.
23.【平行线拐点模型】(12分)
(1)如图①,直线AB∥CD,E是AB与CD之间的一点,连接BE,CE,可以发现:∠B+∠C=∠BEC,请你说明理由;
(2)如果点E运动到图②的位置,其他条件不变,试说明:∠B+∠C=360°-∠BEC;
(3)如图③,AB∥DC,∠C=120°,∠AEC=80°,则∠A= .(直接写出结论,不用写计算过程)
图① 图②
图③
第4章 相交线与平行线
第4章 素养综合检测
1.B (1)同位角只是一种位置关系,只有两条直线平行时,同位角才相等,原说法错误;(2)强调了在平面内,此说法正确;(3)不符合对顶角的定义,原说法错误;(4)直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,不是指点到直线的垂线段,而是指垂线段的长度,原说法错误.故选B.
2.B 根据平移直线AB至CD,可得AB∥CD,所以∠BMF=∠2,根据对顶角相等得∠BMF=∠1=60°,所以∠2=60°.
3.B ∠2与∠5既不是同位角也不是内错角,也不是同旁内角,故符合题意,故选B.
4.B ∵AB∥CD,∴∠1+∠BFE=180°,∵∠AFG=∠BFE,∴∠1+∠AFG=180°,∵∠1与∠CEF是邻补角,∴∠1+∠CEF=180°,∴题图中与∠1互补的角有∠BFE,∠CEF和∠AFG.故选B.
5.C (1)(3)(4)能判定AB∥CD.
6.A 因为AB∥CD,所以∠2+∠CAD+∠1=180°,因为AD⊥AC,所以∠CAD=90°,所以∠1+∠2=90°,所以∠2=90°-55°=35°.
7.D 由图形平移可得出,甲种图形所用铁丝的长度为2a+2b,乙种图形所用铁丝的长度为2a+2b,丙种图形所用铁丝的长度为2a+2b,故三种图形所用铁丝一样长.故选D.
8.C ∵AC⊥BC,CD⊥AB,∴S△ABC=AC·BC=AB·CD,∴CD===,即点C到直线AB的距离为,故选C.
9.B 如图,过B作BF∥AD,∵CE∥AD,∴AD∥BF∥CE,∴∠ABF=∠A=α,∠FBC=180°-∠C,∵∠ABC=∠ABF+∠FBC=β,∴α+180°-∠C=β,
∴∠C=180°-β+α,故选B.
10.A ①∵AB⊥BC,DC⊥BC,∴AB∥CD,∴∠BAD+∠ADC=180°,故①正确;
②∵AB∥CD,∴∠AFD+∠BAF=180°,∵∠BAF=∠EDF,∴∠AFD+∠EDF=180°,∴AF∥DE,故②正确;③∵AF∥ED,∴∠DAF=∠ADE,∠F=∠CDE,∵DE平分∠ADC,∴∠ADE=∠CDE,∴∠DAF=∠F,故③正确.故选A.
11.答案 ∠4(或∠BAE)
解析 根据同旁内角的定义进行分析即可.
12.答案 垂线段最短
解析 直线外一点与直线上各点连接的所有线段中,垂线段最短.
13.答案 100
解析 ∵AB∥CD,∠B=80°,∴∠BCD=∠B=80°,
∵BC∥ED,∴∠D+∠BCD=180°,∴∠D=100°.
易错点 将两直线平行,同旁内角互补误理解为两直线平行,同旁内角相等.
14.答案 10 cm
解析 因为∠D+∠C=180°,所以AD∥BC,因为∠ABC=90°,所以AB的长即为AD与BC之间的距离,因为AB=10 cm,所以AD与BC之间的距离是10 cm.
15.答案 8;下
解析 小金鱼从A点出发,先向左平移8格,再向下平移4格后到达A'点.
16.答案 30°
解析 ∵CM平分∠BCE,∴∠ECM=∠MCB,
∵∠MCN=90°,∴∠BCN+∠MCB=90°,∠DCN+∠MCE=90°,∴∠DCN=∠NCB.∵AB∥CD,
∴∠B=∠BCD=60°,∴∠DCN=30°.
17.答案 ∠B+∠BCD-∠D=180°
解析 如图,过点C作CF∥BA,
∵BA∥DE,∴BA∥CF∥DE,∴∠B+∠BCF=180°,∠FCD=∠D,
∴∠B+∠BCF+∠FCD=180°+∠D,即∠B+∠BCD=180°+∠D,∴∠B+∠BCD-∠D=180°.
18.答案 a1∥a2 024
解析 由题意知a1⊥a2,a1⊥a3,a1∥a4,a1∥a5,……,易知位置关系以4次为一循环.规律:下标除以4,当余数为2或3时,位置关系为垂直,当余数为1或整除时,位置关系为平行,2 024÷4=506,所以a1∥a2 024.
19.解析 (1)如图,PA即为所求.
(2)如图,PB即为所求.
(3)70;70.
详解:∵PA∥ON,∠MON=70°,∴∠PAM=∠MON=70°,∵PB∥OM,∴∠BPA=∠PAM=70°.
20.解析 (1)∵三角形DEF由三角形ABC平移得到,∴∠D=∠A,AB∥DE,
∴∠EMC=∠A,∠AMD=∠A,∴图中与∠A相等的角有3个.
(2)图中的平行线共有2对.由平移的性质可得,AB∥DE,AC∥DF.
(3)由平移的距离可知BE=2 cm,CF=2 cm,∵BC=4 cm,∴BF=6 cm,∴BE∶BC∶BF=2∶4∶6=1∶2∶3.
21.解析 (1)∵∠D+∠AED=180°,
∴AB∥CD.
(2)∵AB∥CD,∴∠DGF=∠EFG,
∵∠C=∠EFG,
∴∠DGF=∠C,
∴CE∥GF,
∵∠CED=75°,∴∠DHG=75°,
∴∠FHD=180°-75°=105°.
22.解析 (1)∵OE平分∠BOC,∴∠BOE=∠COE,
∵∠BOD∶∠BOE=2∶3,
∴∠BOD∶∠BOE∶∠COE=2∶3∶3,
∵∠BOD+∠BOE+∠COE=180°,
∴∠BOD=180°×=45°,
∴∠AOC=∠BOD=45°,
∴∠AOC的度数为45°.
(2)当点F在直线CD的上方时,如图,
∵OF⊥CD,∴∠COF=90°,由(1)得∠AOC=45°,
∴∠AOF=∠AOC+∠COF=135°;
当点F在直线CD的下方时,如图,
∵OF⊥CD,∴∠COF=90°,由(1)得∠AOC=45°,∴∠AOF=∠COF-∠AOC=45°.
综上所述,∠AOF的度数为135°或45°.
23.解析 (1)如图,过点E作EF∥AB,
∵AB∥DC(已知),EF∥AB,
∴EF∥DC(平行于同一直线的两直线平行),
∴∠C=∠CEF(两直线平行,内错角相等).
∵EF∥AB,∴∠B=∠BEF(两直线平行,内错角相等).
∴∠B+∠C=∠BEF+∠CEF,
即∠B+∠C=∠BEC.
(2)如图,过点E作EF∥AB,
∵AB∥DC,EF∥AB,
∴EF∥DC.
∴∠C+∠CEF=180°,
∵EF∥AB,∴∠B+∠BEF=180°.
∴∠B+∠C+∠BEC=360°,
∴∠B+∠C=360°-∠BEC.
(3)20°.详解:如图,过点E作EF∥AB,
∵AB∥DC,EF∥AB,
∴EF∥DC,
∴∠C+∠CEF=180°.
∵∠C=120°,∴∠CEF=180°-120°=60°,
∵∠AEC=80°,∴∠AEF=80°-60°=20°,
∵EF∥AB,∴∠A=∠AEF=20°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024湘教版数学七年级下册
第4章 相交线与平行线
第4章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共30分)
1.【定义法】给出下列说法:
(1)两条直线被第三条直线所截,同位角相等;
(2)平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交;
(3)相等的两个角是对顶角;
(4)从直线外一点到这条直线的垂线段,叫做这点到直线的距离.
其中正确的有( )
A.0个 B.1个 C.2个 D.3个
2.(2023湖南怀化中考)如图,平移直线AB至CD,直线AB,CD被直线EF所截,∠1=60°,则∠2的度数为( )
A.30° B.60°
C.100° D.120°
3.(2023湖北仙桃期中)如图,下列结论中错误的是( )
A.∠3与∠1是同位角
B.∠2与∠5是内错角
C.∠1与∠2是同旁内角
D.∠1与∠6是内错角
4.如图,已知AB∥CD,则图中与∠1互补的角有( )
A.2个 B.3个 C.4个 D.5个
5.(2023湖南湘西州凤凰调研)如图,下列能判定AB∥CD的条件有( )
(1)∠B+∠BCD=180°;(2)∠1=∠2;
(3)∠3=∠4;(4)∠B=∠5.
A.1个 B.2个 C.3个 D.4个
6.(2023重庆中考A卷)如图,AB∥CD,AD⊥AC,若∠1=55°,则∠2的度数为( )
A.35° B.45° C.50° D.55°
7.【新考法】(2023北京一零一中学月考)某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是( )
A.甲种图形所用铁丝最长
B.乙种图形所用铁丝最长
C.丙种图形所用铁丝最长
D.三种图形所用铁丝一样长
8.(2023湖南长沙长郡双语实验中学期中)如图,已知AC⊥BC,CD⊥AB,AC=5,BC=12,AB=13,则点C到直线AB的距离等于( )
A. B. C. D.
9.【平行线拐点模型】(2022山东青岛期末)一条公路修到湖边时,需拐弯绕道而过,第一次拐弯∠A的度数为α,第二次拐弯∠B的度数为β,到了点C后需要继续拐弯,且拐弯后的道路与第一次拐弯之前的道路平行,则∠C的度数为( )
A.α-β B.180°-β+α
C.360°-β-α D.β-α
10.(2023海南琼海期末)如图,AB⊥BC于点B,DC⊥BC于点C,DE平分∠ADC交BC于点E,点F为线段CD延长线上一点,∠BAF=∠EDF,则下列结论正确的有( )
①∠BAD+∠ADC=180°;②AF∥DE;③∠DAF=∠F.
A.3个 B.2个 C.1个 D.0个
二、填空题(每小题3分,共24分)
11.【三线八角模型】如图,∠2的同旁内角是 .
12.【新独家原创】在某市城镇化建设中,燃气公司为某小区P改造供气系统,燃气公司有如下几种连接方式,其中连接处放在C处工程造价最低,其数学道理是 .
13.【易错题】(2023湖南永州中考)如图,AB∥CD,BC∥ED,∠B=80°,则∠D= 度.
如图,∠ABC=90°,AB=10 cm,∠D+∠C=180°,则AD与BC之间的距离是 .
15.如图,正方形网格中有一条小金鱼ABCDEF,小金鱼从A点出发,先向左平移 格,再向 平移4格后到达A'点.
16.(2023湖南永州祁阳期末)如图,已知AB∥CD,∠B=60°,CM平分∠BCE,∠MCN=90°,则∠DCN的度数为 .
第16题图 第17题图
17.【平行线拐点模型】(2023上海外国语大学附属外国语学校期中)如图,BA∥DE,则∠B、∠BCD、∠D的关系是 .
18.【新独家原创】【新考向·规律探究题】在同一平面内有2 024条直线a1,a2,a3,…,a2 024,如果a1⊥a2,a2∥a3,a3⊥a4,a4∥a5,……,那么a1与a2 024的位置关系是 .
三、解答题(共46分)
19. (8分)按要求画图,并回答问题:如图,点P在∠MON的内部.
(1)过点P画PA∥ON,交OM于点A;
(2)过点P画PB∥OM,交ON于点B;
(3)填空:若∠MON=70°,则∠PAM= 度,∠BPA= 度.
20.(2023湖南湘西州龙山期末)(8分)如图所示,已知在三角形ABC中,BC=4 cm,把三角形ABC沿BC方向平移2 cm得到三角形DEF.
(1)图中与∠A相等的角有多少个
(2)图中的平行线共有多少对 请分别写出来.
(3)求BE∶BC∶BF是多少.
21.(2022四川成都外国语学校期中)(8分)如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠D+∠AED=180°,∠C=∠EFG.
(1)试说明:AB∥CD;
(2)若∠CED=75°,求∠FHD的度数.
22.【分类讨论思想】(10分)如图,直线AB、CD相交于点O,OE平分∠BOC,∠BOD∶∠BOE=2∶3.
(1)求∠AOC的度数;
(2)过点O作OF⊥CD于点O,求∠AOF的度数.
23.【平行线拐点模型】(12分)
(1)如图①,直线AB∥CD,E是AB与CD之间的一点,连接BE,CE,可以发现:∠B+∠C=∠BEC,请你说明理由;
(2)如果点E运动到图②的位置,其他条件不变,试说明:∠B+∠C=360°-∠BEC;
(3)如图③,AB∥DC,∠C=120°,∠AEC=80°,则∠A= .(直接写出结论,不用写计算过程)
图① 图②
图③
第4章 相交线与平行线
第4章 素养综合检测
1.B (1)同位角只是一种位置关系,只有两条直线平行时,同位角才相等,原说法错误;(2)强调了在平面内,此说法正确;(3)不符合对顶角的定义,原说法错误;(4)直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,不是指点到直线的垂线段,而是指垂线段的长度,原说法错误.故选B.
2.B 根据平移直线AB至CD,可得AB∥CD,所以∠BMF=∠2,根据对顶角相等得∠BMF=∠1=60°,所以∠2=60°.
3.B ∠2与∠5既不是同位角也不是内错角,也不是同旁内角,故符合题意,故选B.
4.B ∵AB∥CD,∴∠1+∠BFE=180°,∵∠AFG=∠BFE,∴∠1+∠AFG=180°,∵∠1与∠CEF是邻补角,∴∠1+∠CEF=180°,∴题图中与∠1互补的角有∠BFE,∠CEF和∠AFG.故选B.
5.C (1)(3)(4)能判定AB∥CD.
6.A 因为AB∥CD,所以∠2+∠CAD+∠1=180°,因为AD⊥AC,所以∠CAD=90°,所以∠1+∠2=90°,所以∠2=90°-55°=35°.
7.D 由图形平移可得出,甲种图形所用铁丝的长度为2a+2b,乙种图形所用铁丝的长度为2a+2b,丙种图形所用铁丝的长度为2a+2b,故三种图形所用铁丝一样长.故选D.
8.C ∵AC⊥BC,CD⊥AB,∴S△ABC=AC·BC=AB·CD,∴CD===,即点C到直线AB的距离为,故选C.
9.B 如图,过B作BF∥AD,∵CE∥AD,∴AD∥BF∥CE,∴∠ABF=∠A=α,∠FBC=180°-∠C,∵∠ABC=∠ABF+∠FBC=β,∴α+180°-∠C=β,
∴∠C=180°-β+α,故选B.
10.A ①∵AB⊥BC,DC⊥BC,∴AB∥CD,∴∠BAD+∠ADC=180°,故①正确;
②∵AB∥CD,∴∠AFD+∠BAF=180°,∵∠BAF=∠EDF,∴∠AFD+∠EDF=180°,∴AF∥DE,故②正确;③∵AF∥ED,∴∠DAF=∠ADE,∠F=∠CDE,∵DE平分∠ADC,∴∠ADE=∠CDE,∴∠DAF=∠F,故③正确.故选A.
11.答案 ∠4(或∠BAE)
解析 根据同旁内角的定义进行分析即可.
12.答案 垂线段最短
解析 直线外一点与直线上各点连接的所有线段中,垂线段最短.
13.答案 100
解析 ∵AB∥CD,∠B=80°,∴∠BCD=∠B=80°,
∵BC∥ED,∴∠D+∠BCD=180°,∴∠D=100°.
易错点 将两直线平行,同旁内角互补误理解为两直线平行,同旁内角相等.
14.答案 10 cm
解析 因为∠D+∠C=180°,所以AD∥BC,因为∠ABC=90°,所以AB的长即为AD与BC之间的距离,因为AB=10 cm,所以AD与BC之间的距离是10 cm.
15.答案 8;下
解析 小金鱼从A点出发,先向左平移8格,再向下平移4格后到达A'点.
16.答案 30°
解析 ∵CM平分∠BCE,∴∠ECM=∠MCB,
∵∠MCN=90°,∴∠BCN+∠MCB=90°,∠DCN+∠MCE=90°,∴∠DCN=∠NCB.∵AB∥CD,
∴∠B=∠BCD=60°,∴∠DCN=30°.
17.答案 ∠B+∠BCD-∠D=180°
解析 如图,过点C作CF∥BA,
∵BA∥DE,∴BA∥CF∥DE,∴∠B+∠BCF=180°,∠FCD=∠D,
∴∠B+∠BCF+∠FCD=180°+∠D,即∠B+∠BCD=180°+∠D,∴∠B+∠BCD-∠D=180°.
18.答案 a1∥a2 024
解析 由题意知a1⊥a2,a1⊥a3,a1∥a4,a1∥a5,……,易知位置关系以4次为一循环.规律:下标除以4,当余数为2或3时,位置关系为垂直,当余数为1或整除时,位置关系为平行,2 024÷4=506,所以a1∥a2 024.
19.解析 (1)如图,PA即为所求.
(2)如图,PB即为所求.
(3)70;70.
详解:∵PA∥ON,∠MON=70°,∴∠PAM=∠MON=70°,∵PB∥OM,∴∠BPA=∠PAM=70°.
20.解析 (1)∵三角形DEF由三角形ABC平移得到,∴∠D=∠A,AB∥DE,
∴∠EMC=∠A,∠AMD=∠A,∴图中与∠A相等的角有3个.
(2)图中的平行线共有2对.由平移的性质可得,AB∥DE,AC∥DF.
(3)由平移的距离可知BE=2 cm,CF=2 cm,∵BC=4 cm,∴BF=6 cm,∴BE∶BC∶BF=2∶4∶6=1∶2∶3.
21.解析 (1)∵∠D+∠AED=180°,
∴AB∥CD.
(2)∵AB∥CD,∴∠DGF=∠EFG,
∵∠C=∠EFG,
∴∠DGF=∠C,
∴CE∥GF,
∵∠CED=75°,∴∠DHG=75°,
∴∠FHD=180°-75°=105°.
22.解析 (1)∵OE平分∠BOC,∴∠BOE=∠COE,
∵∠BOD∶∠BOE=2∶3,
∴∠BOD∶∠BOE∶∠COE=2∶3∶3,
∵∠BOD+∠BOE+∠COE=180°,
∴∠BOD=180°×=45°,
∴∠AOC=∠BOD=45°,
∴∠AOC的度数为45°.
(2)当点F在直线CD的上方时,如图,
∵OF⊥CD,∴∠COF=90°,由(1)得∠AOC=45°,
∴∠AOF=∠AOC+∠COF=135°;
当点F在直线CD的下方时,如图,
∵OF⊥CD,∴∠COF=90°,由(1)得∠AOC=45°,∴∠AOF=∠COF-∠AOC=45°.
综上所述,∠AOF的度数为135°或45°.
23.解析 (1)如图,过点E作EF∥AB,
∵AB∥DC(已知),EF∥AB,
∴EF∥DC(平行于同一直线的两直线平行),
∴∠C=∠CEF(两直线平行,内错角相等).
∵EF∥AB,∴∠B=∠BEF(两直线平行,内错角相等).
∴∠B+∠C=∠BEF+∠CEF,
即∠B+∠C=∠BEC.
(2)如图,过点E作EF∥AB,
∵AB∥DC,EF∥AB,
∴EF∥DC.
∴∠C+∠CEF=180°,
∵EF∥AB,∴∠B+∠BEF=180°.
∴∠B+∠C+∠BEC=360°,
∴∠B+∠C=360°-∠BEC.
(3)20°.详解:如图,过点E作EF∥AB,
∵AB∥DC,EF∥AB,
∴EF∥DC,
∴∠C+∠CEF=180°.
∵∠C=120°,∴∠CEF=180°-120°=60°,
∵∠AEC=80°,∴∠AEF=80°-60°=20°,
∵EF∥AB,∴∠A=∠AEF=20°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
