【高考专辑】【专题10】2015年高三数学(理)【押题精练】立体几何
文档属性
| 名称 | 【高考专辑】【专题10】2015年高三数学(理)【押题精练】立体几何 |

|
|
| 格式 | zip | ||
| 文件大小 | 565.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-16 00:00:00 | ||
图片预览









文档简介
课件56张PPT。专题10
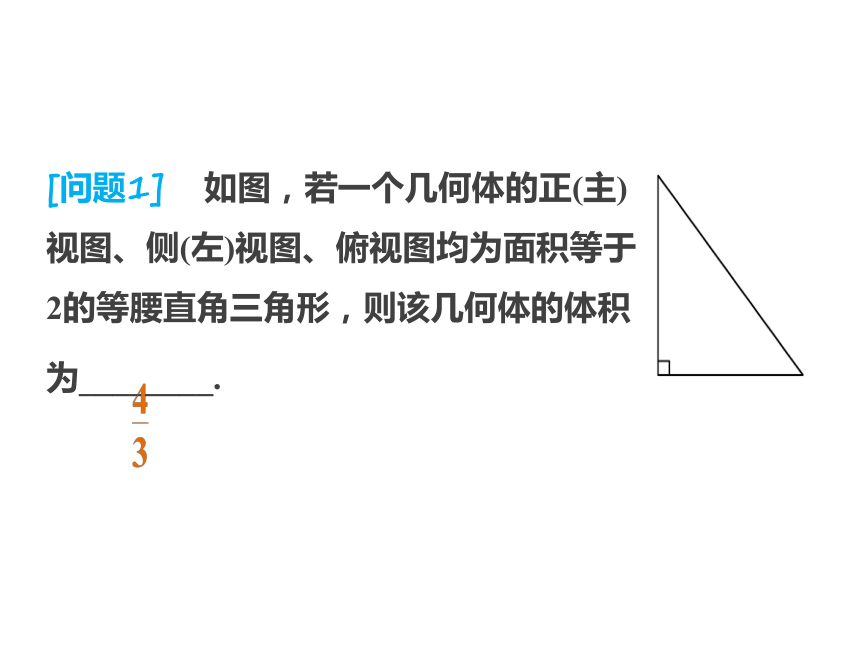
立体几何 立体几何要 点 回 扣易 错 警 示查 缺 补 漏3要点回扣1.一个物体的三视图的排列规则是俯视图放在正(主)视图下面,长度与正(主)视图一样,侧(左)视图放在正(主)视图右面,高度与正(主)视图一样,宽度与俯视图一样,即“长对正,高平齐,宽相等”.在画一个物体的三视图时,一定注意实线与虚线要分明.[问题1] 如图,若一个几何体的正(主)
视图、侧(左)视图、俯视图均为面积等于
2的等腰直角三角形,则该几何体的体积
为________.2.在斜二测画法中,要确定关键点及关键线段.“平行于x轴的线段平行性不变,长度不变;平行于y轴的线段平行性不变,长度减半.”[问题2] 如图所示的等腰直角三角
形表示一个水平放置的平面图形的
直观图,则这个平面图形的面积是
________.(4)圆柱、圆锥、圆台的侧面积公式
S圆柱侧=2πrl(r为底面半径,l为母线),
S圆锥侧=πrl(同上),
S圆台侧=π(r′+r)l(r′、r分别为上、下底的半径,l为母线).
(5)体积公式
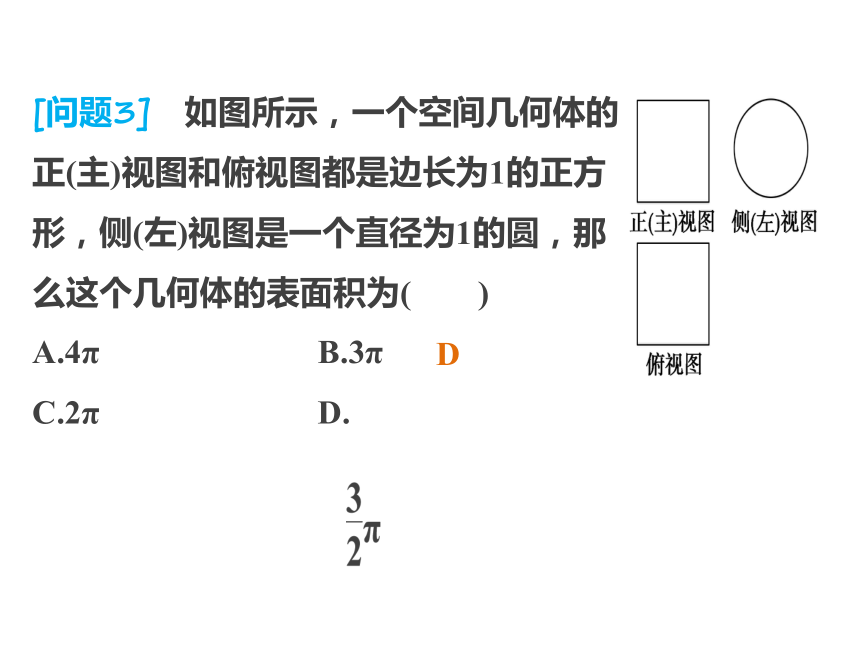
V柱=S·h (S为底面面积,h为高),[问题3] 如图所示,一个空间几何体的
正(主)视图和俯视图都是边长为1的正方
形,侧(左)视图是一个直径为1的圆,那
么这个几何体的表面积为( )
A.4π B.3π
C.2π D.D4.空间直线的位置关系:①相交直线——有且只有一个公共点.②平行直线——在同一平面内,没有公共点.③异面直线——不在同一平面内,也没有公共点.
[问题4] 在空间四边形ABCD中,E、F、G、H分别是四边上的中点,则直线EG和FH的位置关系是________.相交5.空间直线与平面、平面与平面的位置关系
(1)直线与平面
①位置关系:平行、直线在平面内、直线与平面相交.
②直线与平面平行的判定定理和性质定理:
判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.
性质定理:一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行.③直线与平面垂直的判定定理和性质定理:
判定定理:一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直.
性质定理:垂直于同一个平面的两条直线平行.
(2)平面与平面
①位置关系:平行、相交(垂直是相交的一种特殊情况).②平面与平面平行的判定定理和性质定理:
判定定理:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.
性质定理:如果两个平行平面同时和第三个平面相交,那么它们的交线平行.③平面与平面垂直的判定定理和性质定理:
判定定理:一个平面过另一个平面的垂线,则这两个平面垂直.
性质定理:两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.[问题5] 已知b,c是平面α内的两条直线,则“直线a⊥α”是“直线a⊥b,直线a⊥c”的__________条件.充分不必要6.空间向量
(1)用空间向量求角的方法步骤
①异面直线所成的角
若异面直线l1和l2的方向向量分别为v1和v2,它们所成的角为θ,则cos θ=|cos〈v1,v2〉|.
②直线和平面所成的角
利用空间向量求直线与平面所成的角,可以有两种方法:方法一 分别求出斜线和它在平面内的射影直线的方向向量,转化为求两条直线的方向向量的夹角(或其补角).
方法二 通过平面的法向量来求,即求出斜线的方向向量与平面的法向量所夹的锐角,取其余角就是斜线和平面所成的角.③利用空间向量求二面角也有两种方法:
方法一 分别在二面角的两个面内找到一个与棱垂直且从垂足出发的两个向量,则这两个向量的夹角的大小就是二面角的平面角的大小.
方法二 通过平面的法向量来求,设二面角的两个面的法向量分别为n1和n2,则二面角的大小等于〈n1,n2〉(或π-〈n1,n2〉).易错警示:①求线面角时,得到的是直线方向向量和平面法向量的夹角的余弦,容易误以为是线面角的余弦.
②求二面角时,两法向量的夹角有可能是二面角的补角,要注意从图中分析.
(2)用空间向量求A到平面α的距离:
可表示为d= .[问题6] (1)已知正三棱柱ABC-A1B1C1的侧棱长与底面边长相等,则AB1与侧面ACC1A1所成角的正弦值等于________.解析 方法一 取A1C1的中点E,连接
AE,B1E,如图.由题意知B1E⊥平面ACC1A1,
则∠B1AE为AB1与侧面ACC1A1所成的角.设正三棱柱侧棱长与底面边长为1,方法二 如图,以A1C1中点E为原点建立空间直角坐标系
E-xyz,(2)正方体ABCD-A1B1C1D1的棱长为1,O是底面A1B1C1D1的中心,则点O到平面ABC1D1的距离为________.解析 建立如图所示的空间直角坐标系,设平面ABC1D1的法向量为n=(x,y,z),则易错点1 三视图认识不清致误易错点2 对几何概念理解不透致误易错点3 对线面关系定理条件把握不准致误易错警示易错点1 三视图认识不清致误例1 一个空间几何体的三视图如图所示,则该几何体的表面积为( )错解 由三视图知,该几何体的直观图
如图所示,该几何体的下底面是边长为
4的正方形;
上底面是长为4,宽为2的矩形;
两个梯形侧面垂直于底面,上底长为2,下底长为4,高为4;
另两个侧面是正方形,边长为4.所以表面积S=42×3+2×4+2× (2+4)×4
=48+8+24=80.找准失分点不能准确把握三视图和几何体之间的数量关系,根据正视图可知,侧视图中等腰梯形的高为4,而错认为等腰梯形的腰为4.正解 由三视图知该几何体的直观图
如图所示,该几何体的下底面是边长为4的正方形;上底面是长为4、宽为2的矩形;两个梯形侧面垂直于底面,上底长为2,下底长为4,高为4;答案 C易错点2 对几何概念理解不透致误例2 给出下列四个命题:
①有两个平面互相平行,其余各面都是平行四边形的多面体是棱柱;
②若两个过相对侧棱的截面都垂直于底面,则该四棱柱为直四棱柱;
③底面是平行四边形的四棱柱是平行六面体;
④底面是矩形的平行六面体是长方体.
其中正确的命题是__________(写出所有正确命题的序号).找准失分点错解1 ①②③
错解2 ②③④①是错误的,因为棱柱的侧棱要都平行且相等;④是错误的,因为长方体的侧棱必须与底面垂直.正解 ②③易错点3 对线面关系定理条件把握不准致误例3 已知m、n是不同的直线,α、β、γ是不同的平面.给出下列命题:
①若α⊥β,α∩β=m,n⊥m,则n⊥α,或n⊥β;
②若α∥β,α∩γ=m,β∩γ=n,则m∥n;
③若m不垂直于α,则m不可能垂直于α内的无数条直线;
④若α∩β=m,n∥m,且n?α,n?β,则n∥α,且n∥β;
⑤若m、n为异面直线,则存在平面α过m且使n⊥α.
其中正确的命题序号是________.找准失分点错解 ②③④⑤③是错误的;⑤是错误的.正解 ①是错误的.如正方体中面ABB′A′⊥面ADD′A′,
交线为AA′.
直线AC⊥AA′,但AC不垂直面ABB′A′,同时AC也不垂直面ADD′A′.②正确.实质上是两平面平行的性质定理.
③是错误的.在上面的正方体中,A′C不垂直于平面A′B′C′D′,但与B′D′垂直.这样A′C就垂直于平面A′B′C′D′内与直线B′D′平行的无数条直线.
④正确.利用线面平行的判定定理即可.
⑤错误.从结论考虑,若n⊥α且m?α,
则必有m⊥n,事实上,条件并不能保证m⊥n.故错误.
答案 ②④查缺补漏123456789101.已知三条不同直线m,n,l与三个不同平面α,β,γ,有下列命题:
①若m∥α,n∥α,则m∥n;②若α∥β,l?α,则l∥β;③α⊥γ,β⊥γ,则α∥β;④若m,n为异面直线,m?α,n?β,m∥β,n∥α,则α∥β.
其中正确命题的个数是( )
A.0 B.1 C.2 D.3查缺补漏12345678910解析 因为平行于同一平面的两条直线除了平行,还可能相交或成异面直线,所以命题①错误;
由直线与平面平行的定义知命题②正确;
由于垂直于同一个平面的两个平面可能平行还可能相交,因此命题③错误;
过两条异面直线分别作平面互相平行,这两个平面是唯一存在的,因此命题④正确.故选C.
答案 C查缺补漏123456789102.设m,n是空间两条直线,α,β是空间两个平面,则下列选项中不正确的是( )
A.当m?α时,“n∥α”是“m∥n”的必要不充分条件
B.当m?α时,“m⊥β”是“α⊥β”的充分不必要条件
C.当n⊥α时,“n⊥β”是“α∥β”成立的充要条件
D.当m?α时,“n⊥α”是“m⊥n”的充分不必要条件查缺补漏12345678910解析 当m?α时,若n∥α可得m∥n或m,n异面;
若m∥n可得n∥α或n?α,
所以“n∥α”是“m∥n”的既不充分也不必要条件,答案选A.
答案 A查缺补漏123456789103.一个几何体的三视图如图所示,则该几何体的体积是( )A.64 B.72 C.80 D.112查缺补漏12345678910解析 根据三视图,该几何体为下面是一个立方体、上面两个三棱锥,答案 B查缺补漏123456789104.如图所示,在正方体ABCD-A1B1C1D1
中,M,N,P,Q分别是AA1,A1D1,
CC1,BC的中点,给出以下四个结论:
①A1C⊥MN;②A1C∥平面MNPQ;③A1C与PM相交;④NC与PM异面.其中不正确的结论是( )
A.① B.② C.③ D.④查缺补漏12345678910解析 作出过M,N,P,Q四点的截面交
C1D1于点S,交AB于点R,如图所示中的
六边形MNSPQR,显然点A1,C分别位于
这个平面的两侧,故A1C与平面MNPQ一定相交,不可能平行,故结论②不正确.
答案 B查缺补漏123456789105.一个几何体的三视图如图所示,则该几何体的表面积为( )查缺补漏12345678910解析 由三视图可知,该几何体是一个
四棱锥,如图所示.该几何体的底面是边长为1的正方形,
故S1=12=1.侧棱PA⊥面ABCD,且PA=1,查缺补漏12345678910答案 A查缺补漏123456789106.如图,已知六棱锥P—ABCDEF的底面
是正六边形,PA⊥平面ABC,PA=2AB,
则下列结论正确的是( )
A.PB⊥AD
B.平面PAB⊥平面PBC
C.直线BC∥平面PAE
D.直线PD与平面ABC所成的角为45°查缺补漏12345678910解析 若PB⊥AD,则AD⊥AB,但AD与AB成60°角,A错误;
平面PAB与平面ABD垂直,所以平面PAB一定不与平面PBC垂直,B错误;
BC与AE是相交直线,所以BC一定不与平面PAE平行,C错误;查缺补漏12345678910直线PD与平面ABC所成角为∠PDA,在Rt△PAD中,AD=PA,
∴∠PDA=45°,D正确.
答案 D查缺补漏123456789107.对于四面体ABCD,给出下列四个命题:
①若AB=AC,BD=CD,则BC⊥AD;
②若AB=CD,AC=BD,则BC⊥AD;
③若AB⊥AC,BD⊥CD,则BC⊥AD;
④若AB⊥CD,AC⊥BD,则BC⊥AD.
其中正确的是________.(填序号)查缺补漏12345678910解析 取线段BC的中点E,连接AE,DE,
∵AB=AC,BD=CD,
∴BC⊥AE,BC⊥DE,
∴BC⊥平面ADE,
∵AD?平面ADE,
∴BC⊥AD,故①正确.查缺补漏12345678910设点O为点A在平面BCD上的射影,连接OB,OC,OD,
∵AB⊥CD,AC⊥BD,
∴OB⊥CD,OC⊥BD,
∴点O为△BCD的垂心,
∴OD⊥BC,
∴BC⊥AD,故④正确,易知②③不正确,填①④.
答案 ①④查缺补漏12345678910查缺补漏12345678910查缺补漏123456789109.已知直线l,m,平面α,β,且l⊥α,m?β,给出四个命题:
①若α∥β,则l⊥m;②若l⊥m,则α∥β;③若α⊥β,则l∥m;④若l∥m,则α⊥β.
其中为真命题的是________.(填序号)查缺补漏12345678910解析 对命题①,则l⊥α,α∥β得,l⊥β,m?β,
∴l⊥m,故①正确.对命题③,当α⊥β时,l与m也可能相交或异面或平行,故③错误.
对命题④,由l⊥α,l∥m得m⊥α,又m?β,∴α⊥β,故④正确.
答案 ①④对命题②,l⊥m l⊥β,则l⊥m α∥β,故②错误.查缺补漏1234567891010.三棱锥D-ABC及其三视图中的正(主)视图和侧(左)视图如图所示,则棱BD的长为________.查缺补漏12345678910解析 由正(主)视图知CD⊥平面ABC,
设AC中点为E,则BE⊥AC,且AE=CE=2;
立体几何 立体几何要 点 回 扣易 错 警 示查 缺 补 漏3要点回扣1.一个物体的三视图的排列规则是俯视图放在正(主)视图下面,长度与正(主)视图一样,侧(左)视图放在正(主)视图右面,高度与正(主)视图一样,宽度与俯视图一样,即“长对正,高平齐,宽相等”.在画一个物体的三视图时,一定注意实线与虚线要分明.[问题1] 如图,若一个几何体的正(主)
视图、侧(左)视图、俯视图均为面积等于
2的等腰直角三角形,则该几何体的体积
为________.2.在斜二测画法中,要确定关键点及关键线段.“平行于x轴的线段平行性不变,长度不变;平行于y轴的线段平行性不变,长度减半.”[问题2] 如图所示的等腰直角三角
形表示一个水平放置的平面图形的
直观图,则这个平面图形的面积是
________.(4)圆柱、圆锥、圆台的侧面积公式
S圆柱侧=2πrl(r为底面半径,l为母线),
S圆锥侧=πrl(同上),
S圆台侧=π(r′+r)l(r′、r分别为上、下底的半径,l为母线).
(5)体积公式
V柱=S·h (S为底面面积,h为高),[问题3] 如图所示,一个空间几何体的
正(主)视图和俯视图都是边长为1的正方
形,侧(左)视图是一个直径为1的圆,那
么这个几何体的表面积为( )
A.4π B.3π
C.2π D.D4.空间直线的位置关系:①相交直线——有且只有一个公共点.②平行直线——在同一平面内,没有公共点.③异面直线——不在同一平面内,也没有公共点.
[问题4] 在空间四边形ABCD中,E、F、G、H分别是四边上的中点,则直线EG和FH的位置关系是________.相交5.空间直线与平面、平面与平面的位置关系
(1)直线与平面
①位置关系:平行、直线在平面内、直线与平面相交.
②直线与平面平行的判定定理和性质定理:
判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.
性质定理:一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行.③直线与平面垂直的判定定理和性质定理:
判定定理:一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直.
性质定理:垂直于同一个平面的两条直线平行.
(2)平面与平面
①位置关系:平行、相交(垂直是相交的一种特殊情况).②平面与平面平行的判定定理和性质定理:
判定定理:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.
性质定理:如果两个平行平面同时和第三个平面相交,那么它们的交线平行.③平面与平面垂直的判定定理和性质定理:
判定定理:一个平面过另一个平面的垂线,则这两个平面垂直.
性质定理:两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.[问题5] 已知b,c是平面α内的两条直线,则“直线a⊥α”是“直线a⊥b,直线a⊥c”的__________条件.充分不必要6.空间向量
(1)用空间向量求角的方法步骤
①异面直线所成的角
若异面直线l1和l2的方向向量分别为v1和v2,它们所成的角为θ,则cos θ=|cos〈v1,v2〉|.
②直线和平面所成的角
利用空间向量求直线与平面所成的角,可以有两种方法:方法一 分别求出斜线和它在平面内的射影直线的方向向量,转化为求两条直线的方向向量的夹角(或其补角).
方法二 通过平面的法向量来求,即求出斜线的方向向量与平面的法向量所夹的锐角,取其余角就是斜线和平面所成的角.③利用空间向量求二面角也有两种方法:
方法一 分别在二面角的两个面内找到一个与棱垂直且从垂足出发的两个向量,则这两个向量的夹角的大小就是二面角的平面角的大小.
方法二 通过平面的法向量来求,设二面角的两个面的法向量分别为n1和n2,则二面角的大小等于〈n1,n2〉(或π-〈n1,n2〉).易错警示:①求线面角时,得到的是直线方向向量和平面法向量的夹角的余弦,容易误以为是线面角的余弦.
②求二面角时,两法向量的夹角有可能是二面角的补角,要注意从图中分析.
(2)用空间向量求A到平面α的距离:
可表示为d= .[问题6] (1)已知正三棱柱ABC-A1B1C1的侧棱长与底面边长相等,则AB1与侧面ACC1A1所成角的正弦值等于________.解析 方法一 取A1C1的中点E,连接
AE,B1E,如图.由题意知B1E⊥平面ACC1A1,
则∠B1AE为AB1与侧面ACC1A1所成的角.设正三棱柱侧棱长与底面边长为1,方法二 如图,以A1C1中点E为原点建立空间直角坐标系
E-xyz,(2)正方体ABCD-A1B1C1D1的棱长为1,O是底面A1B1C1D1的中心,则点O到平面ABC1D1的距离为________.解析 建立如图所示的空间直角坐标系,设平面ABC1D1的法向量为n=(x,y,z),则易错点1 三视图认识不清致误易错点2 对几何概念理解不透致误易错点3 对线面关系定理条件把握不准致误易错警示易错点1 三视图认识不清致误例1 一个空间几何体的三视图如图所示,则该几何体的表面积为( )错解 由三视图知,该几何体的直观图
如图所示,该几何体的下底面是边长为
4的正方形;
上底面是长为4,宽为2的矩形;
两个梯形侧面垂直于底面,上底长为2,下底长为4,高为4;
另两个侧面是正方形,边长为4.所以表面积S=42×3+2×4+2× (2+4)×4
=48+8+24=80.找准失分点不能准确把握三视图和几何体之间的数量关系,根据正视图可知,侧视图中等腰梯形的高为4,而错认为等腰梯形的腰为4.正解 由三视图知该几何体的直观图
如图所示,该几何体的下底面是边长为4的正方形;上底面是长为4、宽为2的矩形;两个梯形侧面垂直于底面,上底长为2,下底长为4,高为4;答案 C易错点2 对几何概念理解不透致误例2 给出下列四个命题:
①有两个平面互相平行,其余各面都是平行四边形的多面体是棱柱;
②若两个过相对侧棱的截面都垂直于底面,则该四棱柱为直四棱柱;
③底面是平行四边形的四棱柱是平行六面体;
④底面是矩形的平行六面体是长方体.
其中正确的命题是__________(写出所有正确命题的序号).找准失分点错解1 ①②③
错解2 ②③④①是错误的,因为棱柱的侧棱要都平行且相等;④是错误的,因为长方体的侧棱必须与底面垂直.正解 ②③易错点3 对线面关系定理条件把握不准致误例3 已知m、n是不同的直线,α、β、γ是不同的平面.给出下列命题:
①若α⊥β,α∩β=m,n⊥m,则n⊥α,或n⊥β;
②若α∥β,α∩γ=m,β∩γ=n,则m∥n;
③若m不垂直于α,则m不可能垂直于α内的无数条直线;
④若α∩β=m,n∥m,且n?α,n?β,则n∥α,且n∥β;
⑤若m、n为异面直线,则存在平面α过m且使n⊥α.
其中正确的命题序号是________.找准失分点错解 ②③④⑤③是错误的;⑤是错误的.正解 ①是错误的.如正方体中面ABB′A′⊥面ADD′A′,
交线为AA′.
直线AC⊥AA′,但AC不垂直面ABB′A′,同时AC也不垂直面ADD′A′.②正确.实质上是两平面平行的性质定理.
③是错误的.在上面的正方体中,A′C不垂直于平面A′B′C′D′,但与B′D′垂直.这样A′C就垂直于平面A′B′C′D′内与直线B′D′平行的无数条直线.
④正确.利用线面平行的判定定理即可.
⑤错误.从结论考虑,若n⊥α且m?α,
则必有m⊥n,事实上,条件并不能保证m⊥n.故错误.
答案 ②④查缺补漏123456789101.已知三条不同直线m,n,l与三个不同平面α,β,γ,有下列命题:
①若m∥α,n∥α,则m∥n;②若α∥β,l?α,则l∥β;③α⊥γ,β⊥γ,则α∥β;④若m,n为异面直线,m?α,n?β,m∥β,n∥α,则α∥β.
其中正确命题的个数是( )
A.0 B.1 C.2 D.3查缺补漏12345678910解析 因为平行于同一平面的两条直线除了平行,还可能相交或成异面直线,所以命题①错误;
由直线与平面平行的定义知命题②正确;
由于垂直于同一个平面的两个平面可能平行还可能相交,因此命题③错误;
过两条异面直线分别作平面互相平行,这两个平面是唯一存在的,因此命题④正确.故选C.
答案 C查缺补漏123456789102.设m,n是空间两条直线,α,β是空间两个平面,则下列选项中不正确的是( )
A.当m?α时,“n∥α”是“m∥n”的必要不充分条件
B.当m?α时,“m⊥β”是“α⊥β”的充分不必要条件
C.当n⊥α时,“n⊥β”是“α∥β”成立的充要条件
D.当m?α时,“n⊥α”是“m⊥n”的充分不必要条件查缺补漏12345678910解析 当m?α时,若n∥α可得m∥n或m,n异面;
若m∥n可得n∥α或n?α,
所以“n∥α”是“m∥n”的既不充分也不必要条件,答案选A.
答案 A查缺补漏123456789103.一个几何体的三视图如图所示,则该几何体的体积是( )A.64 B.72 C.80 D.112查缺补漏12345678910解析 根据三视图,该几何体为下面是一个立方体、上面两个三棱锥,答案 B查缺补漏123456789104.如图所示,在正方体ABCD-A1B1C1D1
中,M,N,P,Q分别是AA1,A1D1,
CC1,BC的中点,给出以下四个结论:
①A1C⊥MN;②A1C∥平面MNPQ;③A1C与PM相交;④NC与PM异面.其中不正确的结论是( )
A.① B.② C.③ D.④查缺补漏12345678910解析 作出过M,N,P,Q四点的截面交
C1D1于点S,交AB于点R,如图所示中的
六边形MNSPQR,显然点A1,C分别位于
这个平面的两侧,故A1C与平面MNPQ一定相交,不可能平行,故结论②不正确.
答案 B查缺补漏123456789105.一个几何体的三视图如图所示,则该几何体的表面积为( )查缺补漏12345678910解析 由三视图可知,该几何体是一个
四棱锥,如图所示.该几何体的底面是边长为1的正方形,
故S1=12=1.侧棱PA⊥面ABCD,且PA=1,查缺补漏12345678910答案 A查缺补漏123456789106.如图,已知六棱锥P—ABCDEF的底面
是正六边形,PA⊥平面ABC,PA=2AB,
则下列结论正确的是( )
A.PB⊥AD
B.平面PAB⊥平面PBC
C.直线BC∥平面PAE
D.直线PD与平面ABC所成的角为45°查缺补漏12345678910解析 若PB⊥AD,则AD⊥AB,但AD与AB成60°角,A错误;
平面PAB与平面ABD垂直,所以平面PAB一定不与平面PBC垂直,B错误;
BC与AE是相交直线,所以BC一定不与平面PAE平行,C错误;查缺补漏12345678910直线PD与平面ABC所成角为∠PDA,在Rt△PAD中,AD=PA,
∴∠PDA=45°,D正确.
答案 D查缺补漏123456789107.对于四面体ABCD,给出下列四个命题:
①若AB=AC,BD=CD,则BC⊥AD;
②若AB=CD,AC=BD,则BC⊥AD;
③若AB⊥AC,BD⊥CD,则BC⊥AD;
④若AB⊥CD,AC⊥BD,则BC⊥AD.
其中正确的是________.(填序号)查缺补漏12345678910解析 取线段BC的中点E,连接AE,DE,
∵AB=AC,BD=CD,
∴BC⊥AE,BC⊥DE,
∴BC⊥平面ADE,
∵AD?平面ADE,
∴BC⊥AD,故①正确.查缺补漏12345678910设点O为点A在平面BCD上的射影,连接OB,OC,OD,
∵AB⊥CD,AC⊥BD,
∴OB⊥CD,OC⊥BD,
∴点O为△BCD的垂心,
∴OD⊥BC,
∴BC⊥AD,故④正确,易知②③不正确,填①④.
答案 ①④查缺补漏12345678910查缺补漏12345678910查缺补漏123456789109.已知直线l,m,平面α,β,且l⊥α,m?β,给出四个命题:
①若α∥β,则l⊥m;②若l⊥m,则α∥β;③若α⊥β,则l∥m;④若l∥m,则α⊥β.
其中为真命题的是________.(填序号)查缺补漏12345678910解析 对命题①,则l⊥α,α∥β得,l⊥β,m?β,
∴l⊥m,故①正确.对命题③,当α⊥β时,l与m也可能相交或异面或平行,故③错误.
对命题④,由l⊥α,l∥m得m⊥α,又m?β,∴α⊥β,故④正确.
答案 ①④对命题②,l⊥m l⊥β,则l⊥m α∥β,故②错误.查缺补漏1234567891010.三棱锥D-ABC及其三视图中的正(主)视图和侧(左)视图如图所示,则棱BD的长为________.查缺补漏12345678910解析 由正(主)视图知CD⊥平面ABC,
设AC中点为E,则BE⊥AC,且AE=CE=2;
同课章节目录
