【高考专辑】【专题11】2015年高三数学(理)【押题精练】立体几何中的向量方法
文档属性
| 名称 | 【高考专辑】【专题11】2015年高三数学(理)【押题精练】立体几何中的向量方法 |

|
|
| 格式 | zip | ||
| 文件大小 | 737.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-16 00:00:00 | ||
图片预览










文档简介
课件65张PPT。专题11
立体几何中的向量方法立体几何中的向量方法主 干 知 识 梳 理热 点 分 类 突 破真 题 与 押 题3主干知识梳理1.直线与平面、平面与平面的平行与垂直的向量方法
设直线l的方向向量为a=(a1,b1,c1).平面α、β的法向量分别为μ=(a2,b2,c2),v=(a3,b3,c3)(以下相同).
(1)线面平行
l∥α?a⊥μ?a·μ=0?a1a2+b1b2+c1c2=0.(2)线面垂直
l⊥α?a∥μ?a=kμ?a1=ka2,b1=kb2,c1=kc2.
(3)面面平行
α∥β?μ∥v?μ=λv?a2=λa3,b2=λb3,c2=λc3.
(4)面面垂直
α⊥β?μ⊥v?μ·v=0?a2a3+b2b3+c2c3=0.2.直线与直线、直线与平面、平面与平面的夹角计算
设直线l,m的方向向量分别为a=(a1,b1,c1),b=(a2,b2,c2).平面α、β的法向量分别为μ=(a3,b3,c3),v=(a4,b4,c4)(以下相同).
(1)线线夹角(2)线面夹角(3)面面夹角
设半平面α、β的夹角为θ(0≤θ≤π),提醒 求二面角时,两法向量的夹角有可能是二面角的补角,要注意从图中分析.3.求空间距离
直线到平面的距离,两平行平面的距离均可转化为点到平面的距离,点P到平面α的距离:d=
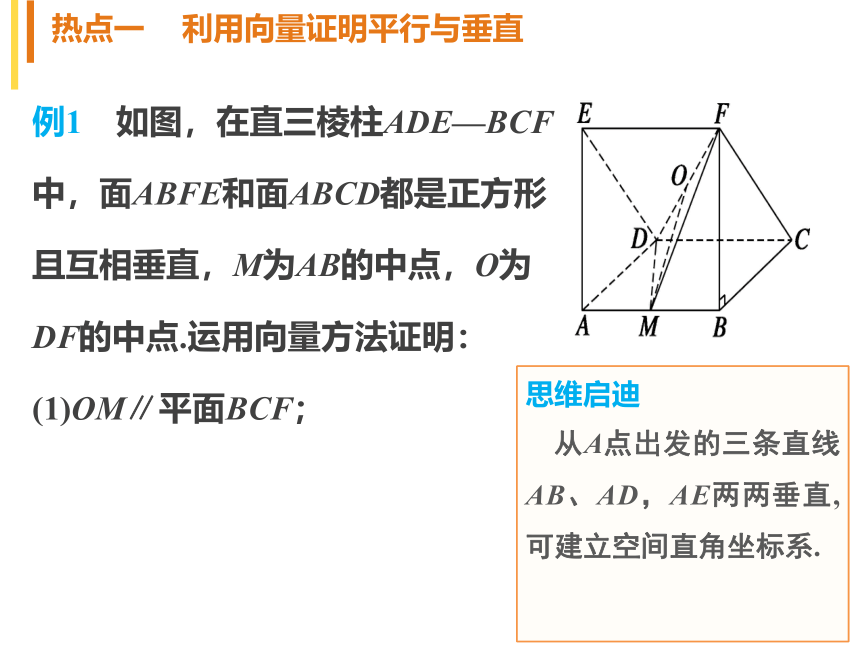
(其中n为α的法向量,M为α内任一点).热点一 利用向量证明平行与垂直热点二 利用向量求空间角热点三 利用空间向量求解探索性问题热点分类突破例1 如图,在直三棱柱ADE—BCF
中,面ABFE和面ABCD都是正方形
且互相垂直,M为AB的中点,O为
DF的中点.运用向量方法证明:
(1)OM∥平面BCF;热点一 利用向量证明平行与垂直思维启迪
从A点出发的三条直线AB、AD,AE两两垂直,可建立空间直角坐标系.证明 方法一 由题意,得AB,AD,AE
两两垂直,以A为原点建立如图所示的空
间直角坐标系.∵棱柱ADE—BCF是直三棱柱,∴AB⊥平面BCF,∴ 是平面BCF的一个法向量,且OM?平面BCF,∴OM∥平面BCF.(2)平面MDF⊥平面EFCD.证明 设平面MDF与平面EFCD的一个法向量分别为
n1=(x1,y1,z1),n2=(x2,y2,z2).同理可得n2=(0,1,1).
∵n1·n2=0,∴平面MDF⊥平面EFCD.又OM?平面BCF,∴OM∥平面BCF.(2)由题意知,BF,BC,BA两两垂直,∴OM⊥CD,OM⊥FC,又CD∩FC=C,
∴OM⊥平面EFCD.
又OM?平面MDF,
∴平面MDF⊥平面EFCD.变式训练1如图,在四棱锥P-ABCD中,PA⊥平
面ABCD,底面ABCD是菱形,PA=AB
=2,∠BAD=60°,E是PA的中点.
(1)求证:直线PC∥平面BDE;证明 设AC∩BD=O.
因为∠BAD=60°,AB=2,底面ABCD为菱形,所以BO=1,AO=CO= ,AC⊥BD.如图,以O为坐标原点,以OB,OC所
在直线分别为x轴,y轴,过点O且平行
于PA的直线为z轴,建立空间直角坐标
系O-xyz,(1)设平面BDE的法向量为n1=(x1,y1,z1),所以PC∥平面BDE.故BD⊥PC.(2)求证:BD⊥PC;例2 如图,五面体中,四边形ABCD
是矩形,AB∥EF,AD⊥平面ABEF,
且AD=1,AB= EF=2,AF=BE=2 ,P、Q分别为AE、BD的中点.
(1)求证:PQ∥平面BCE;热点二 利用向量求空间角思维启迪
易知PQ为△ACE的中位线;证明 连接AC,∵四边形ABCD是矩形,且Q为BD的中点,
∴Q为AC的中点,
又在△AEC中,P为AE的中点,
∴PQ∥EC,
∵EC?面BCE,PQ?面BCE,
∴PQ∥平面BCE.(2)求二面角A-DF-E的余弦值.思维启迪
根据AD⊥平面ABEF构建空间直角坐标系.解 如图,取EF的中点M,则AF⊥AM,
以A为坐标原点,以AM、AF、AD所在直
线分别为x,y,z轴建立空间直角坐标系.则A(0,0,0),D(0,0,1),M(2,0,0),F(0,2,0).令x=1,则y=1,z=2,
故n=(1,1,2)是平面DEF的一个法向量.由图可知所求二面角为锐角,变式训练2 (2013·山东)如图所示,在三棱锥P-ABQ
中,PB⊥平面ABQ,BA=BP=BQ,D,
C,E,F分别是AQ,BQ,AP,BP的中
点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连接GH.(1)求证:AB∥GH;证明 因为D,C,E,F分别是AQ,BQ,AP,BP的中点,
所以EF∥AB,DC∥AB.
所以EF∥DC.又EF?平面PCD,DC?平面PCD,
所以EF∥平面PCD.
又EF?平面EFQ,平面EFQ∩平面PCD=GH,
所以EF∥GH.又EF∥AB,所以AB∥GH.(2)求二面角D-GH-E的余弦值.解 方法一 在△ABQ中,AQ=2BD,AD=DQ,
所以∠ABQ=90°,即AB⊥BQ.
因为PB⊥平面ABQ,所以AB⊥PB.
又BP∩BQ=B,所以AB⊥平面PBQ.
由(1)知AB∥GH,所以GH⊥平面PBQ.
又FH?平面PBQ,所以GH⊥FH.
同理可得GH⊥HC,
所以∠FHC为二面角D-GH-E的平面角.设BA=BQ=BP=2,连接FC,在Rt△FBC中,由勾股定理得FC= ,在Rt△PBC中,由勾股定理得PC= .又H为△PBQ的重心,方法二 在△ABQ中,AQ=2BD,AD=DQ,
所以∠ABQ=90°
又PB⊥平面ABQ,所以BA,BQ,BP两两垂直.以B为坐标原点,分别以BA,BQ,BP
所在直线为x轴,y轴,z轴,建立如图
所示的空间直角坐标系.设BA=BQ=BP=2,则E(1,0,1),F(0,0,1),Q(0,2,0),D(1,1,0),C(0,1,0),P(0,0,2).设平面EFQ的一个法向量为m=(x1,y1,z1),设平面PDC的一个法向量为n=(x2,y2,z2),因为二面角D-GH-E为钝角,所以二面角D-GH-E的余弦值为- .例3 如图,在直三棱柱ABC-A1B1C1中,
AB=BC=2AA1,∠ABC=90°,D是BC
的中点.
(1)求证:A1B∥平面ADC1;热点三 利用空间向量求解探索性问题由ABC-A1B1C1是直三棱柱,得四边形
ACC1A1为矩形,O为A1C的中点.证明 连接A1C,交AC1于点O,连接OD.又D为BC的中点,
所以OD为△A1BC的中位线,
所以A1B∥OD.
因为OD?平面ADC1,A1B?平面ADC1,
所以A1B∥平面ADC1.(2)求二面角C1-AD-C的余弦值;解 由ABC-A1B1C1是直三棱柱,且∠ABC=90°,
得BA,BC,BB1两两垂直.
以BC,BA,BB1所在直线分别为x,y,z轴,建立如图所示的空间直角坐标系B-xyz.设BA=2,则B(0,0,0),C(2,0,0),
A(0,2,0),C1(2,0,1),D(1,0,0),易知平面ADC的一个法向量为v=(0,0,1).因为二面角C1-AD-C是锐二面角,所以二面角C1-AD-C的余弦值为 .(3)试问线段A1B1上是否存在点E,使AE与DC1成60°角?若存在,确定E点位置;若不存在,说明理由.解 假设存在满足条件的点E.
因为点E在线段A1B1上,A1(0,2,1),B1(0,0,1),
故可设E(0,λ,1),其中0≤λ≤2.因为AE与DC1成60°角,所以当点E为线段A1B1的中点时,AE与DC1成60°角.变式训练3如图,在三棱锥P—ABC中,AC=BC
=2,∠ACB=90°,AP=BP=AB,
PC⊥AC,点D为BC的中点.
(1)求二面角A—PD—B的余弦值;解 ∵AC=BC,PA=PB,PC=PC,
∴△PCA≌△PCB,
∴∠PCA=∠PCB,∵PC⊥AC,∴PC⊥CB,
又AC∩CB=C,
∴PC⊥平面ACB,且PC,CA,CB两两垂直,故以C为坐标原点,分别以CB,CA,CP
所在直线为x,y,z轴建立空间直角坐标系,则C(0,0,0),A(0,2,0),D(1,0,0),P(0,0,2),设平面PAD的一个法向量为n=(x,y,z),设二面角A—PD—B的平面角为θ,且θ为钝角,(2)在直线AB上是否存在点M,使得PM与平面PAD所成角的正弦值为 ,若存在,求出点M的位置;若不存在,说明理由.解 方法一 存在,M是AB的中点或A是MB的中点.解得x=1或x=-2,∴M(1,1,0)或M(-2,4,0),∴在直线AB上存在点M,且当M是AB的中点或A是MB的中点时,使得PM与平面PAD所成角的正弦值为 .方法二 存在,M是AB的中点或A是MB的中点.∴M是AB的中点或A是MB的中点.∴在直线AB上存在点M,且当M是AB的中点或A是MB的中点时,使得PM与平面PAD所成角的正弦值为 .空间向量在处理空间问题时具有很大的优越性,能把“非运算”问题“运算”化,即通过直线的方向向量和平面的法向量,把立体几何中的平行、垂直关系,各类角、距离以向量的方式表达出来,把立体几何问题转化为空间向量的运算问题.应用的核心是充分认识形体特征,进而建立空间直角坐标系,通过向量的运算解答问题,达到几何问题代数化的目的,同时注意运算的准确性.本讲规律总结提醒三点:(1)直线的方向向量和平面的法向量所成角的余弦值的绝对值是线面角的正弦值,而不是余弦值.
(2)求二面角除利用法向量外,还可以按照二面角的平面角的定义和空间任意两个向量都是共面向量的知识,我们只要是在二面角的两个半平面内分别作和二面角的棱垂直的向量,并且两个向量的方向均指向棱或者都从棱指向外,那么这两个向量所成的角的大小就是二面角的大小.如图所示.真题感悟押题精练真题与押题真题感悟(2014·北京)如图,正方形AMDE的边长为2,B,C分别为AM,MD的中点,在五棱锥P-ABCDE中,F为棱PE的中点,平面ABF与棱PD,PC分别交于点G,H.真题感悟(1)求证:AB∥FG;证明 在正方形AMDE中,因为B是AM的中点,
所以AB∥DE.
又因为AB?平面PDE,DE?平面PDE,
所以AB∥平面PDE.
因为AB?平面ABF,且平面ABF∩平面PDE=FG,
所以AB∥FG.真题感悟(2)若PA⊥底面ABCDE,且PA=AE,求直线BC与平面ABF所成角的大小,并求线段PH的长.解 因为PA⊥底面ABCDE,
所以PA⊥AB,PA⊥AE.如图建立空间直角坐标系Axyz,则A(0,0,0),B(1,0,0),C(2,1,0),
P(0,0,2),F(0,1,1), =(1,1,0).真题感悟设平面ABF的一个法向量为n=(x,y,z),令z=1,则y=-1,所以n=(0,-1,1).
设直线BC与平面ABF所成角为α,真题感悟设点H的坐标为(u,v,w).即(u,v,w-2)=λ(2,1,-2),
所以u=2λ,v=λ,w=2-2λ.真题感悟即(0,-1,1)·(2λ,λ,2-2λ)=0,押题精练如图所示,已知正方形ABCD和矩形ACEF所在的
平面互相垂直,AB= ,AF=1.
(1)求直线DF与平面ACEF所成角的正弦值;解 以C为坐标原点,分别以CD,CB,CE
所在直线为x轴,y轴,z轴,建立如图所示
的空间直角坐标系,押题精练因为平面ABCD⊥平面ACEF,且平面ABCD∩平面ACEF=AC,押题精练押题精练
立体几何中的向量方法立体几何中的向量方法主 干 知 识 梳 理热 点 分 类 突 破真 题 与 押 题3主干知识梳理1.直线与平面、平面与平面的平行与垂直的向量方法
设直线l的方向向量为a=(a1,b1,c1).平面α、β的法向量分别为μ=(a2,b2,c2),v=(a3,b3,c3)(以下相同).
(1)线面平行
l∥α?a⊥μ?a·μ=0?a1a2+b1b2+c1c2=0.(2)线面垂直
l⊥α?a∥μ?a=kμ?a1=ka2,b1=kb2,c1=kc2.
(3)面面平行
α∥β?μ∥v?μ=λv?a2=λa3,b2=λb3,c2=λc3.
(4)面面垂直
α⊥β?μ⊥v?μ·v=0?a2a3+b2b3+c2c3=0.2.直线与直线、直线与平面、平面与平面的夹角计算
设直线l,m的方向向量分别为a=(a1,b1,c1),b=(a2,b2,c2).平面α、β的法向量分别为μ=(a3,b3,c3),v=(a4,b4,c4)(以下相同).
(1)线线夹角(2)线面夹角(3)面面夹角
设半平面α、β的夹角为θ(0≤θ≤π),提醒 求二面角时,两法向量的夹角有可能是二面角的补角,要注意从图中分析.3.求空间距离
直线到平面的距离,两平行平面的距离均可转化为点到平面的距离,点P到平面α的距离:d=
(其中n为α的法向量,M为α内任一点).热点一 利用向量证明平行与垂直热点二 利用向量求空间角热点三 利用空间向量求解探索性问题热点分类突破例1 如图,在直三棱柱ADE—BCF
中,面ABFE和面ABCD都是正方形
且互相垂直,M为AB的中点,O为
DF的中点.运用向量方法证明:
(1)OM∥平面BCF;热点一 利用向量证明平行与垂直思维启迪
从A点出发的三条直线AB、AD,AE两两垂直,可建立空间直角坐标系.证明 方法一 由题意,得AB,AD,AE
两两垂直,以A为原点建立如图所示的空
间直角坐标系.∵棱柱ADE—BCF是直三棱柱,∴AB⊥平面BCF,∴ 是平面BCF的一个法向量,且OM?平面BCF,∴OM∥平面BCF.(2)平面MDF⊥平面EFCD.证明 设平面MDF与平面EFCD的一个法向量分别为
n1=(x1,y1,z1),n2=(x2,y2,z2).同理可得n2=(0,1,1).
∵n1·n2=0,∴平面MDF⊥平面EFCD.又OM?平面BCF,∴OM∥平面BCF.(2)由题意知,BF,BC,BA两两垂直,∴OM⊥CD,OM⊥FC,又CD∩FC=C,
∴OM⊥平面EFCD.
又OM?平面MDF,
∴平面MDF⊥平面EFCD.变式训练1如图,在四棱锥P-ABCD中,PA⊥平
面ABCD,底面ABCD是菱形,PA=AB
=2,∠BAD=60°,E是PA的中点.
(1)求证:直线PC∥平面BDE;证明 设AC∩BD=O.
因为∠BAD=60°,AB=2,底面ABCD为菱形,所以BO=1,AO=CO= ,AC⊥BD.如图,以O为坐标原点,以OB,OC所
在直线分别为x轴,y轴,过点O且平行
于PA的直线为z轴,建立空间直角坐标
系O-xyz,(1)设平面BDE的法向量为n1=(x1,y1,z1),所以PC∥平面BDE.故BD⊥PC.(2)求证:BD⊥PC;例2 如图,五面体中,四边形ABCD
是矩形,AB∥EF,AD⊥平面ABEF,
且AD=1,AB= EF=2,AF=BE=2 ,P、Q分别为AE、BD的中点.
(1)求证:PQ∥平面BCE;热点二 利用向量求空间角思维启迪
易知PQ为△ACE的中位线;证明 连接AC,∵四边形ABCD是矩形,且Q为BD的中点,
∴Q为AC的中点,
又在△AEC中,P为AE的中点,
∴PQ∥EC,
∵EC?面BCE,PQ?面BCE,
∴PQ∥平面BCE.(2)求二面角A-DF-E的余弦值.思维启迪
根据AD⊥平面ABEF构建空间直角坐标系.解 如图,取EF的中点M,则AF⊥AM,
以A为坐标原点,以AM、AF、AD所在直
线分别为x,y,z轴建立空间直角坐标系.则A(0,0,0),D(0,0,1),M(2,0,0),F(0,2,0).令x=1,则y=1,z=2,
故n=(1,1,2)是平面DEF的一个法向量.由图可知所求二面角为锐角,变式训练2 (2013·山东)如图所示,在三棱锥P-ABQ
中,PB⊥平面ABQ,BA=BP=BQ,D,
C,E,F分别是AQ,BQ,AP,BP的中
点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连接GH.(1)求证:AB∥GH;证明 因为D,C,E,F分别是AQ,BQ,AP,BP的中点,
所以EF∥AB,DC∥AB.
所以EF∥DC.又EF?平面PCD,DC?平面PCD,
所以EF∥平面PCD.
又EF?平面EFQ,平面EFQ∩平面PCD=GH,
所以EF∥GH.又EF∥AB,所以AB∥GH.(2)求二面角D-GH-E的余弦值.解 方法一 在△ABQ中,AQ=2BD,AD=DQ,
所以∠ABQ=90°,即AB⊥BQ.
因为PB⊥平面ABQ,所以AB⊥PB.
又BP∩BQ=B,所以AB⊥平面PBQ.
由(1)知AB∥GH,所以GH⊥平面PBQ.
又FH?平面PBQ,所以GH⊥FH.
同理可得GH⊥HC,
所以∠FHC为二面角D-GH-E的平面角.设BA=BQ=BP=2,连接FC,在Rt△FBC中,由勾股定理得FC= ,在Rt△PBC中,由勾股定理得PC= .又H为△PBQ的重心,方法二 在△ABQ中,AQ=2BD,AD=DQ,
所以∠ABQ=90°
又PB⊥平面ABQ,所以BA,BQ,BP两两垂直.以B为坐标原点,分别以BA,BQ,BP
所在直线为x轴,y轴,z轴,建立如图
所示的空间直角坐标系.设BA=BQ=BP=2,则E(1,0,1),F(0,0,1),Q(0,2,0),D(1,1,0),C(0,1,0),P(0,0,2).设平面EFQ的一个法向量为m=(x1,y1,z1),设平面PDC的一个法向量为n=(x2,y2,z2),因为二面角D-GH-E为钝角,所以二面角D-GH-E的余弦值为- .例3 如图,在直三棱柱ABC-A1B1C1中,
AB=BC=2AA1,∠ABC=90°,D是BC
的中点.
(1)求证:A1B∥平面ADC1;热点三 利用空间向量求解探索性问题由ABC-A1B1C1是直三棱柱,得四边形
ACC1A1为矩形,O为A1C的中点.证明 连接A1C,交AC1于点O,连接OD.又D为BC的中点,
所以OD为△A1BC的中位线,
所以A1B∥OD.
因为OD?平面ADC1,A1B?平面ADC1,
所以A1B∥平面ADC1.(2)求二面角C1-AD-C的余弦值;解 由ABC-A1B1C1是直三棱柱,且∠ABC=90°,
得BA,BC,BB1两两垂直.
以BC,BA,BB1所在直线分别为x,y,z轴,建立如图所示的空间直角坐标系B-xyz.设BA=2,则B(0,0,0),C(2,0,0),
A(0,2,0),C1(2,0,1),D(1,0,0),易知平面ADC的一个法向量为v=(0,0,1).因为二面角C1-AD-C是锐二面角,所以二面角C1-AD-C的余弦值为 .(3)试问线段A1B1上是否存在点E,使AE与DC1成60°角?若存在,确定E点位置;若不存在,说明理由.解 假设存在满足条件的点E.
因为点E在线段A1B1上,A1(0,2,1),B1(0,0,1),
故可设E(0,λ,1),其中0≤λ≤2.因为AE与DC1成60°角,所以当点E为线段A1B1的中点时,AE与DC1成60°角.变式训练3如图,在三棱锥P—ABC中,AC=BC
=2,∠ACB=90°,AP=BP=AB,
PC⊥AC,点D为BC的中点.
(1)求二面角A—PD—B的余弦值;解 ∵AC=BC,PA=PB,PC=PC,
∴△PCA≌△PCB,
∴∠PCA=∠PCB,∵PC⊥AC,∴PC⊥CB,
又AC∩CB=C,
∴PC⊥平面ACB,且PC,CA,CB两两垂直,故以C为坐标原点,分别以CB,CA,CP
所在直线为x,y,z轴建立空间直角坐标系,则C(0,0,0),A(0,2,0),D(1,0,0),P(0,0,2),设平面PAD的一个法向量为n=(x,y,z),设二面角A—PD—B的平面角为θ,且θ为钝角,(2)在直线AB上是否存在点M,使得PM与平面PAD所成角的正弦值为 ,若存在,求出点M的位置;若不存在,说明理由.解 方法一 存在,M是AB的中点或A是MB的中点.解得x=1或x=-2,∴M(1,1,0)或M(-2,4,0),∴在直线AB上存在点M,且当M是AB的中点或A是MB的中点时,使得PM与平面PAD所成角的正弦值为 .方法二 存在,M是AB的中点或A是MB的中点.∴M是AB的中点或A是MB的中点.∴在直线AB上存在点M,且当M是AB的中点或A是MB的中点时,使得PM与平面PAD所成角的正弦值为 .空间向量在处理空间问题时具有很大的优越性,能把“非运算”问题“运算”化,即通过直线的方向向量和平面的法向量,把立体几何中的平行、垂直关系,各类角、距离以向量的方式表达出来,把立体几何问题转化为空间向量的运算问题.应用的核心是充分认识形体特征,进而建立空间直角坐标系,通过向量的运算解答问题,达到几何问题代数化的目的,同时注意运算的准确性.本讲规律总结提醒三点:(1)直线的方向向量和平面的法向量所成角的余弦值的绝对值是线面角的正弦值,而不是余弦值.
(2)求二面角除利用法向量外,还可以按照二面角的平面角的定义和空间任意两个向量都是共面向量的知识,我们只要是在二面角的两个半平面内分别作和二面角的棱垂直的向量,并且两个向量的方向均指向棱或者都从棱指向外,那么这两个向量所成的角的大小就是二面角的大小.如图所示.真题感悟押题精练真题与押题真题感悟(2014·北京)如图,正方形AMDE的边长为2,B,C分别为AM,MD的中点,在五棱锥P-ABCDE中,F为棱PE的中点,平面ABF与棱PD,PC分别交于点G,H.真题感悟(1)求证:AB∥FG;证明 在正方形AMDE中,因为B是AM的中点,
所以AB∥DE.
又因为AB?平面PDE,DE?平面PDE,
所以AB∥平面PDE.
因为AB?平面ABF,且平面ABF∩平面PDE=FG,
所以AB∥FG.真题感悟(2)若PA⊥底面ABCDE,且PA=AE,求直线BC与平面ABF所成角的大小,并求线段PH的长.解 因为PA⊥底面ABCDE,
所以PA⊥AB,PA⊥AE.如图建立空间直角坐标系Axyz,则A(0,0,0),B(1,0,0),C(2,1,0),
P(0,0,2),F(0,1,1), =(1,1,0).真题感悟设平面ABF的一个法向量为n=(x,y,z),令z=1,则y=-1,所以n=(0,-1,1).
设直线BC与平面ABF所成角为α,真题感悟设点H的坐标为(u,v,w).即(u,v,w-2)=λ(2,1,-2),
所以u=2λ,v=λ,w=2-2λ.真题感悟即(0,-1,1)·(2λ,λ,2-2λ)=0,押题精练如图所示,已知正方形ABCD和矩形ACEF所在的
平面互相垂直,AB= ,AF=1.
(1)求直线DF与平面ACEF所成角的正弦值;解 以C为坐标原点,分别以CD,CB,CE
所在直线为x轴,y轴,z轴,建立如图所示
的空间直角坐标系,押题精练因为平面ABCD⊥平面ACEF,且平面ABCD∩平面ACEF=AC,押题精练押题精练
同课章节目录
