【高考专辑】【专题12】2015年高三数学(理)【押题精练】解析几何
文档属性
| 名称 | 【高考专辑】【专题12】2015年高三数学(理)【押题精练】解析几何 |  | |
| 格式 | zip | ||
| 文件大小 | 466.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-16 18:38:35 | ||
图片预览










文档简介
课件66张PPT。专题12
解析几何 解析几何要 点 回 扣易 错 警 示查 缺 补 漏3要点回扣1.直线的倾斜角与斜率
(1)倾斜角的范围为[0,π).
(2)直线的斜率
①定义:倾斜角不是90°的直线,它的倾斜角的正切值叫这条直线的斜率k,即k=tan α(α≠90°);倾斜角为90°的直线没有斜率;②斜率公式:经过两点P1(x1,y1)、P2(x2,y2)的直线的斜率为k= (x1≠x2);③直线的方向向量a=(1,k);④应用:证明三点共线:kAB=kBC.[问题1] (1)直线的倾斜角θ越大,斜率k就越大,这种说法正确吗?
答案 错(2)直线xcos θ+ y-2=0的倾斜角的范围是________________.2.直线的方程
(1)点斜式:已知直线过点(x0,y0),其斜率为k,则直线方程为y-y0=k(x-x0),它不包括垂直于x轴的直线.
(2)斜截式:已知直线在y轴上的截距为b,斜率为k,则直线方程为y=kx+b,它不包括垂直于x轴的直线.(5)一般式:任何直线均可写成Ax+By+C=0(A,B不同时为0)的形式.[问题2] 已知直线过点P(1,5),且在两坐标轴上的截距相等,则此直线的方程为_________________
_______.5x-y=0或x+y-6=03.点到直线的距离及两平行直线间的距离[问题3] 两平行直线3x+2y-5=0与6x+4y+5=0
间的距离为________.4.两直线的平行与垂直
①l1:y=k1x+b1,l2:y=k2x+b2(两直线斜率存在,且不重合),则有l1∥l2?k1=k2;l1⊥l2?k1·k2=-1.
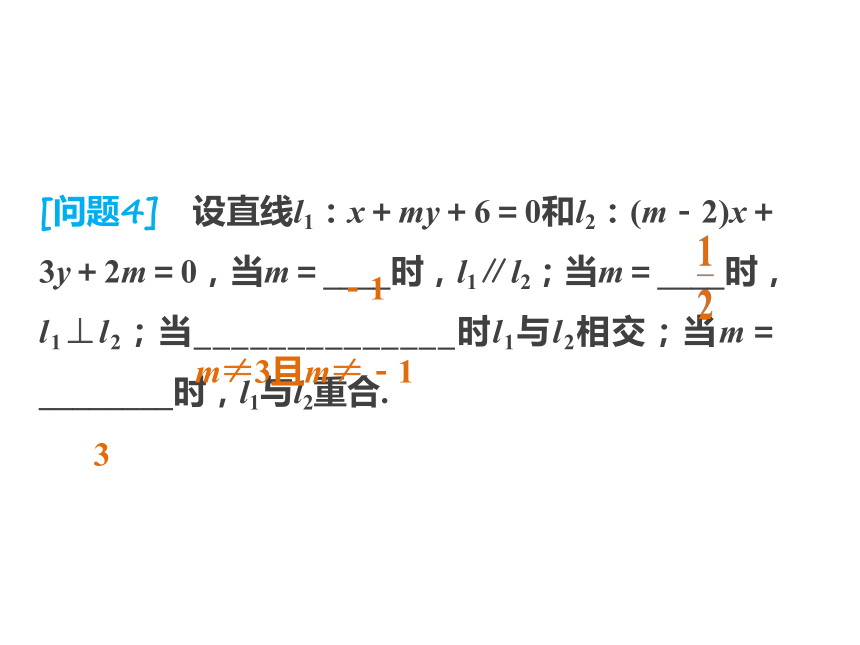
②l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0,则有l1∥l2?A1B2-A2B1=0且B1C2-B2C1≠0;l1⊥l2?A1A2+B1B2=0.[问题4] 设直线l1:x+my+6=0和l2:(m-2)x+3y+2m=0,当m=____时,l1∥l2;当m=____时,l1⊥l2;当______________时l1与l2相交;当m=________时,l1与l2重合.-1m≠3且m≠-135.圆的方程
(1)圆的标准方程:(x-a)2+(y-b)2=r2.
(2)圆的一般方程:x2+y2+Dx+Ey+F=0(D2+E2-4F>0),只有当D2+E2-4F>0时,方程x2+y2+Dx+Ey+F=0才表示圆心为( ),半径为
的圆.[问题5] 若方程a2x2+(a+2)y2+2ax+a=0表示圆,则a=________.-16.直线、圆的位置关系
(1)直线与圆的位置关系
直线l:Ax+By+C=0和圆C:(x-a)2+(y-b)2=r2(r>0)有相交、相离、相切.可从代数和几何两个方面来判断:
①代数方法(判断直线与圆方程联立所得方程组的解的情况):Δ>0?相交;Δ<0?相离;Δ=0?相切;②几何方法(比较圆心到直线的距离与半径的大小):设圆心到直线的距离为d,则dr?相离;d=r?相切.
(2)圆与圆的位置关系
已知两圆的圆心分别为O1,O2,半径分别为r1,r2,则①当|O1O2|>r1+r2时,两圆外离;②当|O1O2|=r1+r2时,两圆外切;③当|r1-r2|<|O1O2|迹方程是______________.8.求椭圆、双曲线及抛物线的标准方程,一般遵循先定位,再定型,后定量的步骤,即先确定焦点的位置,再设出其方程,求出待定系数.(4)抛物线标准方程
焦点在x轴上:y2=±2px(p>0);
焦点在y轴上:x2=±2py(p>0).9.(1)在用圆锥曲线与直线联立求解时,消元后得到的方程中要注意二次项的系数是否为零,利用解的情况可判断位置关系:有两解时相交;无解时相离;有唯一解时,在椭圆中相切.在双曲线中需注意直线与渐近线的关系,在抛物线中需注意直线与对称轴的关系,而后判断是否相切.(2)直线与圆锥曲线相交时的弦长问题
斜率为k的直线与圆锥曲线交于两点P1(x1,y1),P2(x2,y2),则所得弦长[问题9] 已知F是抛物线y2=x的焦点,A,B是该抛物线上的两点,|AF|+|BF|=3,则线段AB的中点到y轴的距离为________.易错点1 直线倾斜角与斜率关系不清致误易错点2 忽视斜率不存在情形致误易错点3 忽视“判别式”致误易错警示易错点1 直线倾斜角与斜率关系不清致误例1 已知直线xsin α+y=0,则该直线的倾斜角的变化范围是__________.错解 由题意得,直线xsin α+y=0的斜率
k=-sin α,
∵-1≤sin α≤1,∴-1≤k≤1,找准失分点直线斜率k=tan β(β为直线的倾斜角)在[0,π)上是不单调的且不连续.正解 由题意得,直线xsin α+y=0的斜率
k=-sin α,
∵-1≤sin α≤1,∴-1≤k≤1,易错点2 忽视斜率不存在情形致误例2 已知直线l1:(t+2)x+(1-t)y=1与l2:(t-1)x+(2t+3)y+2=0互相垂直,则t的值为________.∵l1⊥l2,∴k1·k2=-1,找准失分点(1)盲目认为两直线的斜率存在,忽视对参数的讨论.(2)忽视两直线有一条直线斜率为0,另一条直线斜率不存在时,两直线垂直这一情形.正解 方法一 (1)当l1,l2的斜率都存在时,
由k1·k2=-1得,t=-1.
(2)若l1的斜率不存在,显然l1⊥l2,符合条件;易知l1与l2不垂直,综上t=-1或t=1.
方法二 l1⊥l2?(t+2)(t-1)+(1-t)(2t+3)=0?t=1或t=-1.
答案 -1或1易错点3 忽视“判别式”致误例3 已知双曲线x2- =1,过点A(1,1)能否作直线l,使l与双曲线交于P、Q两点,并且A为线段PQ的中点?若存在,求出直线l的方程;若不存在,说明理由.错解1 设被A(1,1)所平分的弦所在直线方程为
y=k(x-1)+1.整理得(2-k2)x2+2k(k-1)x-3+2k-k2=0,
设直线与双曲线交点为M(x1,y1),N(x2,y2),故所求直线方程为2x-y-1=0.错解2 设符合题意的直线l存在,并设P(x1,y1),Q(x2,y2),因为A(1,1)为线段PQ的中点,所以符合题设条件的直线的方程为2x-y-1=0.找准失分点没有判断直线2x-y-1=0与双曲线是否相交.正解1 设被A(1,1)所平分的弦所在直线方程为
y=k(x-1)+1.(2-k2)x2+2k(k-1)x-3+2k-k2=0,由Δ=4k2(k-1)2-4(2-k2)(2k-3-k2)>0,设直线与双曲线交点为M(x1,y1),N(x2,y2),故不存在被点A(1,1)平分的弦.正解2 设符合题意的直线l存在,并设P(x1,y1)、Q(x2,y2),因为A(1,1)为线段PQ的中点,所以直线l的方程为2x-y-1=0,根据Δ=-8<0,所以所求直线不存在.查缺补漏123456789101.(2014·安徽)过点P( ,-1)的直线l与圆x2+y2=1有公共点,则直线l的倾斜角的取值范围是( )查缺补漏12345678910解析 方法一 如图,过点P作圆的切线
PA,PB,切点为A,B.由题意知|OP|=2,OA=1,所以α=30°,∠BPA=60°.查缺补漏12345678910答案 D查缺补漏12345678910A.焦距相等 B.实半轴长相等
C.虚半轴长相等 D.离心率相等查缺补漏12345678910解析 因为0答案 A查缺补漏12345678910查缺补漏12345678910解析 由于m、n可互换而不影响,查缺补漏12345678910答案 D查缺补漏12345678910查缺补漏12345678910查缺补漏12345678910答案 C查缺补漏12345678910查缺补漏12345678910如图,过Q作QQ′⊥l,垂足为Q′,设l与x轴的交点为A,则|AF|=4,∴|QQ′|=3,根据抛物线定义可知|QQ′|=|QF|=3,故选C.
答案 C查缺补漏123456789106.(2014·陕西)若圆C的半径为1,其圆心与点(1,0)关于直线y=x对称,则圆C的标准方程为______________.解析 圆C的圆心为(0,1),半径为1,
标准方程为x2+(y-1)2=1.x2+(y-1)2=1查缺补漏12345678910解析 ①当斜率k不存在时,过点P的直线方程为x=-3,
代入x2+y2=25,得y1=4,y2=-4.
所以弦长为|y1-y2|=8,符合题意.查缺补漏12345678910查缺补漏12345678910即3x+4y+15=0.
所以所求直线方程为x+3=0或3x+4y+15=0.
答案 x+3=0或3x+4y+15=0查缺补漏123456789108.在平面直角坐标系xOy中,圆C的方程为x2+y2-8x+15=0,若直线y=kx-2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,则k的最大值是________.解析 圆C的标准方程为(x-4)2+y2=1,圆心为(4,0).由题意知(4,0)到kx-y-2=0的距离应不大于2,查缺补漏12345678910查缺补漏12345678910其中一条渐近线方程为bx-ay=0,查缺补漏12345678910答案 2查缺补漏12345678910查缺补漏12345678910查缺补漏12345678910设直线l:x-3y+m=0(m≠0),
因为|PA|=|PB|,所以PC⊥l,
所以kPC=-3,化简得a2=4b2.
在双曲线中,c2=a2+b2=5b2,
解析几何 解析几何要 点 回 扣易 错 警 示查 缺 补 漏3要点回扣1.直线的倾斜角与斜率
(1)倾斜角的范围为[0,π).
(2)直线的斜率
①定义:倾斜角不是90°的直线,它的倾斜角的正切值叫这条直线的斜率k,即k=tan α(α≠90°);倾斜角为90°的直线没有斜率;②斜率公式:经过两点P1(x1,y1)、P2(x2,y2)的直线的斜率为k= (x1≠x2);③直线的方向向量a=(1,k);④应用:证明三点共线:kAB=kBC.[问题1] (1)直线的倾斜角θ越大,斜率k就越大,这种说法正确吗?
答案 错(2)直线xcos θ+ y-2=0的倾斜角的范围是________________.2.直线的方程
(1)点斜式:已知直线过点(x0,y0),其斜率为k,则直线方程为y-y0=k(x-x0),它不包括垂直于x轴的直线.
(2)斜截式:已知直线在y轴上的截距为b,斜率为k,则直线方程为y=kx+b,它不包括垂直于x轴的直线.(5)一般式:任何直线均可写成Ax+By+C=0(A,B不同时为0)的形式.[问题2] 已知直线过点P(1,5),且在两坐标轴上的截距相等,则此直线的方程为_________________
_______.5x-y=0或x+y-6=03.点到直线的距离及两平行直线间的距离[问题3] 两平行直线3x+2y-5=0与6x+4y+5=0
间的距离为________.4.两直线的平行与垂直
①l1:y=k1x+b1,l2:y=k2x+b2(两直线斜率存在,且不重合),则有l1∥l2?k1=k2;l1⊥l2?k1·k2=-1.
②l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0,则有l1∥l2?A1B2-A2B1=0且B1C2-B2C1≠0;l1⊥l2?A1A2+B1B2=0.[问题4] 设直线l1:x+my+6=0和l2:(m-2)x+3y+2m=0,当m=____时,l1∥l2;当m=____时,l1⊥l2;当______________时l1与l2相交;当m=________时,l1与l2重合.-1m≠3且m≠-135.圆的方程
(1)圆的标准方程:(x-a)2+(y-b)2=r2.
(2)圆的一般方程:x2+y2+Dx+Ey+F=0(D2+E2-4F>0),只有当D2+E2-4F>0时,方程x2+y2+Dx+Ey+F=0才表示圆心为( ),半径为
的圆.[问题5] 若方程a2x2+(a+2)y2+2ax+a=0表示圆,则a=________.-16.直线、圆的位置关系
(1)直线与圆的位置关系
直线l:Ax+By+C=0和圆C:(x-a)2+(y-b)2=r2(r>0)有相交、相离、相切.可从代数和几何两个方面来判断:
①代数方法(判断直线与圆方程联立所得方程组的解的情况):Δ>0?相交;Δ<0?相离;Δ=0?相切;②几何方法(比较圆心到直线的距离与半径的大小):设圆心到直线的距离为d,则d
(2)圆与圆的位置关系
已知两圆的圆心分别为O1,O2,半径分别为r1,r2,则①当|O1O2|>r1+r2时,两圆外离;②当|O1O2|=r1+r2时,两圆外切;③当|r1-r2|<|O1O2|
焦点在x轴上:y2=±2px(p>0);
焦点在y轴上:x2=±2py(p>0).9.(1)在用圆锥曲线与直线联立求解时,消元后得到的方程中要注意二次项的系数是否为零,利用解的情况可判断位置关系:有两解时相交;无解时相离;有唯一解时,在椭圆中相切.在双曲线中需注意直线与渐近线的关系,在抛物线中需注意直线与对称轴的关系,而后判断是否相切.(2)直线与圆锥曲线相交时的弦长问题
斜率为k的直线与圆锥曲线交于两点P1(x1,y1),P2(x2,y2),则所得弦长[问题9] 已知F是抛物线y2=x的焦点,A,B是该抛物线上的两点,|AF|+|BF|=3,则线段AB的中点到y轴的距离为________.易错点1 直线倾斜角与斜率关系不清致误易错点2 忽视斜率不存在情形致误易错点3 忽视“判别式”致误易错警示易错点1 直线倾斜角与斜率关系不清致误例1 已知直线xsin α+y=0,则该直线的倾斜角的变化范围是__________.错解 由题意得,直线xsin α+y=0的斜率
k=-sin α,
∵-1≤sin α≤1,∴-1≤k≤1,找准失分点直线斜率k=tan β(β为直线的倾斜角)在[0,π)上是不单调的且不连续.正解 由题意得,直线xsin α+y=0的斜率
k=-sin α,
∵-1≤sin α≤1,∴-1≤k≤1,易错点2 忽视斜率不存在情形致误例2 已知直线l1:(t+2)x+(1-t)y=1与l2:(t-1)x+(2t+3)y+2=0互相垂直,则t的值为________.∵l1⊥l2,∴k1·k2=-1,找准失分点(1)盲目认为两直线的斜率存在,忽视对参数的讨论.(2)忽视两直线有一条直线斜率为0,另一条直线斜率不存在时,两直线垂直这一情形.正解 方法一 (1)当l1,l2的斜率都存在时,
由k1·k2=-1得,t=-1.
(2)若l1的斜率不存在,显然l1⊥l2,符合条件;易知l1与l2不垂直,综上t=-1或t=1.
方法二 l1⊥l2?(t+2)(t-1)+(1-t)(2t+3)=0?t=1或t=-1.
答案 -1或1易错点3 忽视“判别式”致误例3 已知双曲线x2- =1,过点A(1,1)能否作直线l,使l与双曲线交于P、Q两点,并且A为线段PQ的中点?若存在,求出直线l的方程;若不存在,说明理由.错解1 设被A(1,1)所平分的弦所在直线方程为
y=k(x-1)+1.整理得(2-k2)x2+2k(k-1)x-3+2k-k2=0,
设直线与双曲线交点为M(x1,y1),N(x2,y2),故所求直线方程为2x-y-1=0.错解2 设符合题意的直线l存在,并设P(x1,y1),Q(x2,y2),因为A(1,1)为线段PQ的中点,所以符合题设条件的直线的方程为2x-y-1=0.找准失分点没有判断直线2x-y-1=0与双曲线是否相交.正解1 设被A(1,1)所平分的弦所在直线方程为
y=k(x-1)+1.(2-k2)x2+2k(k-1)x-3+2k-k2=0,由Δ=4k2(k-1)2-4(2-k2)(2k-3-k2)>0,设直线与双曲线交点为M(x1,y1),N(x2,y2),故不存在被点A(1,1)平分的弦.正解2 设符合题意的直线l存在,并设P(x1,y1)、Q(x2,y2),因为A(1,1)为线段PQ的中点,所以直线l的方程为2x-y-1=0,根据Δ=-8<0,所以所求直线不存在.查缺补漏123456789101.(2014·安徽)过点P( ,-1)的直线l与圆x2+y2=1有公共点,则直线l的倾斜角的取值范围是( )查缺补漏12345678910解析 方法一 如图,过点P作圆的切线
PA,PB,切点为A,B.由题意知|OP|=2,OA=1,所以α=30°,∠BPA=60°.查缺补漏12345678910答案 D查缺补漏12345678910A.焦距相等 B.实半轴长相等
C.虚半轴长相等 D.离心率相等查缺补漏12345678910解析 因为0
答案 C查缺补漏123456789106.(2014·陕西)若圆C的半径为1,其圆心与点(1,0)关于直线y=x对称,则圆C的标准方程为______________.解析 圆C的圆心为(0,1),半径为1,
标准方程为x2+(y-1)2=1.x2+(y-1)2=1查缺补漏12345678910解析 ①当斜率k不存在时,过点P的直线方程为x=-3,
代入x2+y2=25,得y1=4,y2=-4.
所以弦长为|y1-y2|=8,符合题意.查缺补漏12345678910查缺补漏12345678910即3x+4y+15=0.
所以所求直线方程为x+3=0或3x+4y+15=0.
答案 x+3=0或3x+4y+15=0查缺补漏123456789108.在平面直角坐标系xOy中,圆C的方程为x2+y2-8x+15=0,若直线y=kx-2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,则k的最大值是________.解析 圆C的标准方程为(x-4)2+y2=1,圆心为(4,0).由题意知(4,0)到kx-y-2=0的距离应不大于2,查缺补漏12345678910查缺补漏12345678910其中一条渐近线方程为bx-ay=0,查缺补漏12345678910答案 2查缺补漏12345678910查缺补漏12345678910查缺补漏12345678910设直线l:x-3y+m=0(m≠0),
因为|PA|=|PB|,所以PC⊥l,
所以kPC=-3,化简得a2=4b2.
在双曲线中,c2=a2+b2=5b2,
同课章节目录
